顾及系统偏差的BDS铁路边坡监测方法

何义磊,张云龙,张冠军,胡锦民,陈旭升

(1. 中国铁路设计集团有限公司,天津 300308; 2. 天津市轨道交通导航定位及时空大数据技术重点实验室,天津 300251)

当前我国铁路事业正迅猛发展,截至2021年末,全国铁路营业总里程已突破15万km,铁路工程基础设施建设和运营维护的需求日渐增加。我国幅员辽阔,山地众多,特别是西北黄土高原,土质松软,在极端天气或施工扰动情况下,滑坡和泥石流等突发地质灾害严重威胁铁路工程施工建设与运营,边坡的稳定性对地面设施、人身安全及工程进度影响巨大[1]。受内外多种不确定性因素的影响,运动规律难以掌控,除了采取必要的防护措施外,还应进行实时监测,以掌握边坡变化趋势并及时预警,为铁路工程建设与维护提供技术支撑和安全保障[2]。

GNSS具有自动化程度高、全天候观测、测点间无需通视、可快速获取高精度三维信息等特点[3],被广泛应用于边坡、桥梁、大坝等大型工程的变形监测[4],可满足西北部山区恶劣的工程环境和铁路遮挡环境下快速高精度的监测需求。由于GPS成熟较早,诸多学者已通过静态相对定位技术、RTK技术、精密单点定位(precise point positioning,PPP)技术等多种数据处理方式,对GPS变形监测技术进行研究,并取得了良好效果[5-8]。静态相对定位和RTK技术均需基准站提供差分信息或进行双差。然而在土质松软地区,基准站的稳定性将严重影响定位精度,选择可独立观测且定位精度相当的PPP技术对获取高精度位置信息具有重要意义。文献[7]采用PPP技术对高层建筑的倾斜和沉降进行长期监测,通过稳定的局部参考框架和当地季节性地面变形模型相结合的方式得出,华北地区PPP平面和高程精度分别达到2～3 mm和6～9 mm(24 h连续观测)。文献[8]研究了复杂艰险地区的铁路场景下,顾及相位偏差的GPS PPP定位性能,结果表明水平和高程方向定位精度分别优于10、15 cm(90 min连续观测)。

北斗卫星导航系统(BeiDou Navigation Satellite System,BDS)于2020年7月31日全面建成,现阶段处于北斗二号(BDS-2,15颗)/北斗三号(BDS-3,30颗)共存的局面,并向全球用户提供高精度的导航、定位、授时服务,其卫星数量、信号质量、定位性能均显著提升[9-11]。BDS的广泛应用和GNSS接收机的国产化是必然趋势,然而有研究表明多系统组合PPP中存在系统偏差(inter-system bias, ISB)。文献[12]基于无电离层组合解算GPS+BDS ISB,发现ISB大小与接收机类型相关,大小为10～100 ns;文献[13]针对7 d的MGEX(multi-GNSS experiment)跟踪网观测数据,基于GPS+BDS组合PPP模型解算GPS、BDS短期ISB,并构建二次多项式加周期函数的短期ISB预报模型,建议预报时长为1 d,利用预报ISB作为先验信息进行组合PPP,发现在N、E、U方向上的定位精度和收敛效率有所提升。文献[14]针对MGEX跟踪网2014—2016年各7 d的数据,基于BDS+GPS组合PPP模型分别解算4个跟踪站的ISB值,以分析ISB的长期稳定性,结果表明ISB序列的天变化较为稳定,而3年的ISB周平均值和标准差(standard deviation,STD)具有显著差异。因此,为提升遮挡环境下的定位性能,需削弱ISB的影响。

本文以西北地区某铁路隧道南侧山体的边坡北斗监测工程为例,详细介绍利用BDS PPP技术进行边坡变形监测的方法,并对BDS-2、BDS-3间ISB进行估计、分析和建模,将预报ISB作为先验约束加入BDS-2+BDS-3组合PPP中,以检验PPP定位精度和收敛时间的提升水平,并对案例中的监测点进行稳定性分析。

1 顾及ISB的BDS PPP基本理论

图1为2021年12月1日BDS在轨运行卫星星下点轨迹。BDS-3卫星在BDS-2卫星播发B1I和B3I信号的基础上,新增观测数据质量更佳的B1C和B2a信号[15],同时应用了新的卫星姿态模型、新型原子钟等技术。因此本文将两者视为两个不同的卫星导航系统,重点分析BDS-3卫星B1C和B2a信号与BDS-2卫星组合PPP的性能水平。

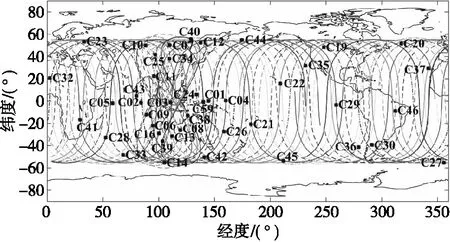
图1 2021年12月1日BDS在轨运行卫星星下点轨迹

1.1 顾及ISB的GPS+BDS-2+BDS-3组合PPP模型

接收机R与卫星S在原始伪距和载波相位观测值的观测方程为[16]

δion+δrel+δmult+εR(P)

(1)

δion+δrel+δmult+εR(Φ)

(2)

式中,S为GPS+BDS-2+BDS-3卫星;ρ为卫星和接收机天线相位中心间的几何距离;c为真空中的光速;dtR为接收机钟差;dtS为卫星钟差;bR、bS、Br、Bs分别为接收机和卫星的硬件延迟;δion为电离层延迟误差;δtrop为对流层延迟误差;δrel为相对论效应误差;δmult为多路径效应误差;N为载波相位整周模糊度;ε(P)和ε(Φ)分别为伪距和载波相位观测噪声等未模型化的参数[16]。

基于双频伪距和载波相位观测值的无电离层组合,式(1)—式(2)可分别转换为

(3)

(4)

利用精密卫星轨道和钟差,式(3)—式(4)可分别转换为

(5)

(6)

(7)

ISB参数(ISBG,B2和ISBG,B3)可与其他参数一同被估计,两者相减可得到BDS-2和BDS-3间的系统偏差ISBB2,B3,即

ISBB2,B3=ISBG,B3-ISBG,B2

(8)

在ISB被忽略或已知时,可通过式(1)—式(7)实现GPS+BDS-2+BDS-3组合PPP。

1.2 基于N次多项式+ARIMA的ISB模型

针对ISBB2,B3序列中未含有周期项,提出一种基于N次多项式+自回归移动平均模型(autoregressive integrated moving average model,ARIMA)的组合建模方法[16]。利用N次多项式对原始ISB＿O序列进行最小二乘拟合[16],即

ISB＿Ft=antn+an-1tn-1+…+a1t+a0

(9)

式中,ISB＿Ft表示第t个历元ISBB2,B3的拟合值;an和a0为N次项和常量项的系数。通过计算ISB＿O与ISB＿F残差序列的RMS,确定最佳拟合次数。

利用ARIMA对残差序列进行建模,ARIMA(p,d,q)模型可表示为[17]

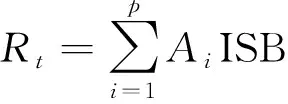
(10)

式中,ISB＿Rt为ISB＿Ot和ISB＿Ft之差;A、B和p、q分别为ARIMA模型的系数和阶数;v为误差项,{vi}～WN(0,δ2),WN为白噪声。

ISB＿Pt+1预报值可表示为

ISB＿Pt+1=a8(t+1)8+…+a1(t+1)+a0+

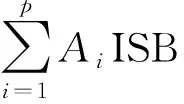
(11)

式中,各项系数均可由式(9)、式(10)得到。为了减弱历史数据的影响,采用滑动窗口的策略。

2 BDS-2、BDS-3间ISB特性分析及模型构建

2.1 数据获取与处理

选取2021年12月1—31日(年积日335—365)西北地区某铁路隧道南侧山体高边坡BJ01和BC01北斗监测站数据,接收机类型为SEPT MOSAIC-X5C,天线类型为HGGCYH8373 HGGS,可同时接收GPS、BDS-2、BDS-3信号,采样间隔30 s。图2为BJ01和BC01北斗监测站示意图,其中BJ01建在稳定的开阔区域,BC01建在高边坡顶端,周边植被丛生,遮挡严重。该边坡为高山峡谷地貌,地形陡峭,坡度一般为30°～50°。边坡多为泥石流堆积体和发育滑坡,南侧受336国道施工扰动,为避免滑坡威胁铁路安全,需对其进行自动化实时监测。

图2 BJ01和BC01北斗监测站示意

2.2 BDS-2+BDS-3组合PPP中ISB特性分析

对估计的BDS-2、BDS-3间系统偏差ISBB2,B3日稳定性进行分析,探究其短期变化规律。图3为BJ01和BC01监测站年积日335—348为期14 d的原始ISBB2,B3序列。

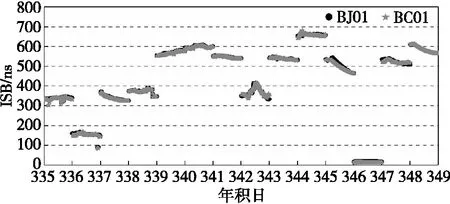
图3 BJ01和BC01监测站ISBB2,B3时序

由图3可以看出,BJ01和BC01北斗监测站ISBB2,B3在0～700 ns之间波动,一天内变化较为平稳,呈多条连续且平顺的曲线,但天与天之间存在跳变,呈阶梯状。分别计算两个监测站单日的ISBB2,B3平均值和标准差,其中年积日344时两站单日ISBB2,B3平均值均为最大,分别为660、658 ns,14 d的ISBB2,B3平均值分别470、467 ns,因此ISBB2,B3的存在已严重影响到PPP定位精度。而14 d的ISBB2,B3标准差的平均值均为10 ns,表明ISBB2,B3在一天内的变化较为稳定。两站天与天之间的ISBB2,B3存在跳变,且表现出良好的一致性,该跳变是由估计卫星精密钟差时更换参考星所致[16]。因此需要先消除跳变的影响,跳变修复的公式为

(12)

Δd=ISB(Ti)-ISB(Ti-1)

(13)

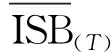
图4为跳变修复后的ISBB2,B3序列,可以看出,原序列中存在的跳变被修复,但由某些未得到修复的小跳变的积累导致年积日343后BJ01和BC01站的ISB序列产生明显差异。

图4 BJ01和BC01监测站修复跳变后ISBB2,B3时序

2.3 基于N次多项式+ARIMA的BDS-2、BDS-3间ISB模型

利用快速傅里叶变换(fast Fourier transform, FFT)对修复后的ISBB2,B3序列进行频谱分析。图5为BJ01和BC01站ISBB2,B3序列的功率谱密度(power spectral density,PSD)。可以看出,只有一个明显信号频率为零,表明序列ISBB2,B3不含有周期项。

图5 监测站修复跳变后ISBB2,B3的PSD

为得到最佳的多项式系数,利用最小二乘法估计BJ01和BC01站1～100次多项式拟合的系数。次数为8时,拟合系数最佳。采用八次多项式(octave polynomial,OP)对原始ISBB2,B3序列进行拟合。表1为年积日308—321,BJ01和BC01站的基于OP拟合的各次项和常数项系数。图6为BJ01和BC01站的拟合结果。

表1 年积日335—348时BJ01和BC01北斗监测站的ISBB2,B3八次多项式拟合系数

图6 监测站八次多项式拟合ISBB2,B3结果

采用ARIMA对ISBB2,B3原始序列ISB＿O和八次多项式拟合的序列ISB＿P之间的残差序列进行建模。使用Eviews 9.0软件构建ARIMA(p,d,q)模型,得到BJ01和BC01站的ARIMA(p,d,q)模型参数、残差方差、AIC和SC信息准则值,见表2。图7为年积日335—348时BJ01和BC01站的ISBB2,B3残差序列拟合结果,ISB＿f表示拟合值。

表2 BJ01和BC01站的ARIMA模型参数和结果

图7 ISBB2,B3残差拟合结果

本文以平均绝对误差(mean absolute error,MAE)和均方根误差(root mean square error,RMSE)作为ISB建模与预测的精度指标。MAE表示为

(14)

式中,ISB＿Ot、ISB＿Ft、ISB＿ft分别为t时刻ISB的原始估计值、八次多项式、ARIMA模型拟合值。评估ISB的预报精度时用ISB＿Pt代替(ISB＿Ft+ISB＿ft)拟合值。

图8为基于OP+ARIMA的ISBB2,B3拟合结果。可以看出,ISB＿F与ISB＿O非常吻合,残差序列ISB＿R较为稳定,大多数情况下近似为0。BJ01和BC01站拟合残差的MAE分别为0.17、0.19 ns,RMSE分别为0.50、0.54 ns,表明本文ISB建模方法具有较高的拟合精度。

图8 北斗监测站ISBB2,B3拟合结果

为了验证OP+ARIMA模型的预报精度,利用以年积日335—348两周的原始ISB＿O序列为基础构建的模型,预报年积日349的ISB＿P,并与同期估计的ISB＿O进行比较。图9为年积日349时BJ01和BC01站ISBB2,B3的预报结果。可以看出,预报早期ISB＿O与ISB＿P具有较好的一致性,但随着时间的推移,预报残差ISB＿R变大,准确性有所降低。两站ISB＿R的MAE分别为1.322、2.365 ns,RMSE分别为1.623、3.145 ns,表明本文ISB模型具有较高的精度。为了保证预报的ISB精度,建议以14 d为时长建模,预报时长为1 d,若进行长时间预报,滑动窗口大小为14 d。

图9 年积日349北斗监测站ISBB2,B3预报结果

2.4 顾及ISB约束的BDS PPP定位性能分析

为了验证OP+ARIMA模型ISB预报值的可用性,针对年积日349时BJ01和BC01北斗监测站作静态PPP试验,根据两站的地理位置,可分别模拟开阔环境下和遮挡环境下的PPP验证;同时将上述预报的ISB视为先验约束,ISB预报残差的RMSE作为先验精度。按如下两种方案进行数据处理,并比较其在N、E、U方向的收敛时间和定位精度。收敛时刻以定位误差小于0.1 m的时刻,且其后20个时刻的误差均满足要求为准则[13]。

(1)GPS、BDS-2和BDS-3组合PPP时,不考虑之间的ISB,将两者视为同一系统。

(2)GPS、BDS-2和BDS-3组合PPP时,将预报的BDS-2、BDS-3间系统偏差ISB＿P作为先验约束。

图10为BJ01北斗监测站0～3 h的PPP收敛时序。可以直观地看出,N、E、U方向均在短时间内达到收敛要求,随后曲线保持平稳,在附加ISB先验约束后收敛时间缩短,N方向优于E和U方向。表3和图11为BJ01和BC01北斗监测站在顾及ISB约束前后的定位精度和收敛时间的对比。可以看出,在增加预报ISB作为约束条件后,BJ01站在N、E、U方向上的定位精度分别提升了6.25%、4.23%、4.66%,收敛时间分别缩短了5.71%、7.14%、11.11%;BC01站在N、E、U方向上的定位精度分别提升了9.24%、16.02%、8.46%,收敛时间分别缩短了9.30%、15.59%、15.00%。

表3 BJ01和BC01站在两种方案下的定位精度和收敛时间对比 (%)

图10 年积日349 BJ01北斗监测站PPP收敛时序

图11 年积日349 BJ01和BC01北斗监测站顾及ISB约束的PPP定位精度和收敛时间

结果表明,在观测环境较好的情况下增加ISB的约束可提升定位精度和解算效率,而在卫星数较少或现场存在遮挡的情况下增加ISB的约束,可显著提升定位精度和解算效率,在铁路高边坡自动化监测中具有良好的适用性。

2.5 监测点变形分析

利用本文顾及ISB约束的BDS-2+BDS-3组合PPP,对BJ01和BC01北斗监测站在年积日335—365间的点位进行估计,分析监测点的变形情况。以年积日328—334(7 d)的坐标平均值为参考值,图12为BJ01和BC01两监测站的坐标变化。由于静态相对定位技术可消除卫星端、接收机端、大气等误差影响,而受多路径影响较大,以此验证顾及ISB约束的BDS-2+BDS-3组合PPP的定位精度。图12为BJ01和BC01北斗监测站静态相对定位结果及其与PPP的比较。

图12 年积日335—365 BJ01和BC01北斗监测站坐标变化

由图12可知,BJ01北斗监测站在年积日335—365一个月内基本稳定,无异常形变,在N、E、U方向的最大形变量分别为4.10、7.05、7.01 mm,RMSE分别为1.85、3.08、4.13 mm。对于BC01北斗监测站,在年积日352后E和U方向发生明显形变,年积日365时N、E、U方向的形变量分别为0.97、-22.33、-19.17 mm,年积日335—365内RMSE分别为2.60、11.10、9.64 mm。由于BJ01站基本稳定,BC01和BJ01站间静态相对定位结果即为BC01站的变形量。如图13所示,静态相对定位结果与BC01站PPP结果表现一致,在年积日352后E和U方向发生明显变形,年积日365时N、E、U方向的变形量分别为0.30、-21.40、-17.70 mm。静态相对定位结果与BC01和BJ01站间PPP坐标差在N、E、U方向的RMSE分别为1.26、2.11、2.22 mm。表明本文方法适用于遮挡环境下铁路边坡长期静态变形监测,监测精度可达毫米级。

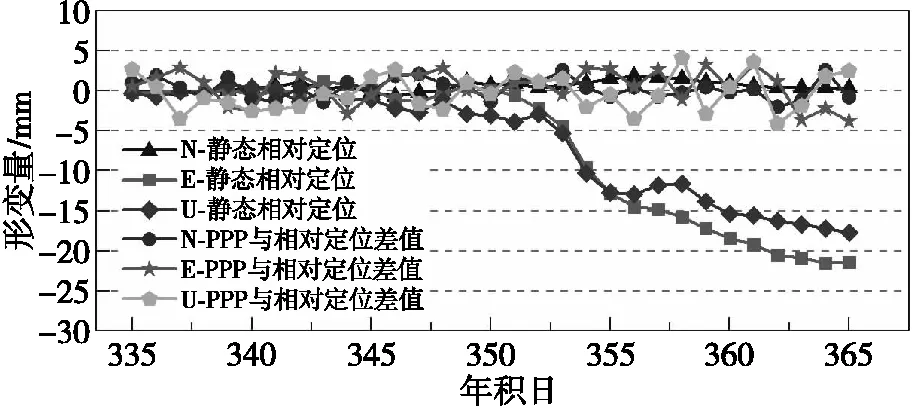
图13 年积日335—365 BJ01和BC01北斗监测站相对定位

3 结 论

本文详细介绍了顾及BDS-2、BDS-3间ISB的铁路边坡自动化监测方法;以某铁路隧道边坡工程监测为例,在PPP中估计了BDS-2、BDS-3间的ISB,并分析了ISB短期特性;提出了八次多项式+自回归移动平均模型的ISB建模方法,验证了模型精度和该方法对PPP定位性能的改进;分析了BJ01和BC01监测点为期一个月的稳定性,主要结论如下。

(1)提出了GPS+BDS-2+BDS-3组合PPP估计ISB的解算方法,分析了BDS-2和BDS-3间的系统偏差ISBB2,B3的短期稳定性,其14 d的平均值量级约为470 ns,但单日内变化较小,天与天之间存在数百纳秒的跳变,在BDS-2(B1I,B3I)和BDS-3(B1C,B2a)组合PPP中,需考虑其影响。

(2)分析表明ISB序列中不含周期项,提出OP+ARIMA的ISB建模方法,以为期14 d的ISB序列进行建模,在预报时长为1 d时,该方法具有较高的拟合精度和较好的一致性,预报精度随时间推移有所降低。

(3)将预报的ISB作为先验约束,应用于BDS-2+BDS-3组合PPP中,可在复杂的观测环境下提升解算效率和定位精度。

(4)对于BJ01北斗监测站在年积日335—365一个月内基本稳定,BC01北斗监测站在年积日352后发生明显形变,与静态相对定位结果相近,监测精度可达毫米级,能满足西北山区铁路边坡长期静态变形监测的需求。