基于循环谱相关的编码器信号滚动轴承故障检测
2023-09-05杨新敏
田 田, 郭 瑜, 杨新敏, 邹 翔, 陈 鑫
(昆明理工大学 机电工程学院, 昆明 650500)
目前,基于振动信号的滚动轴承故障检测是滚动轴承故障诊断研究的主要方向之一,但振动信号获取需要在被监测对象上安装振动传感器,对于工作过程存在较大范围复合运动的工业机器人关节(RV减速器)等振动传感器的安装易影响工业机器人的使用,对此类设备轴承故障检测亟待研究新的途径。
相较于振动信号,编码器信号具有:等角度采样、无时变传递路径、在具备伺服控制的旋转机械中无需安装传感器等优点[1]。编码器信号可直接反应扭矩的变化,在齿轮故障特征提取研究中表现较好。然而,轴承作为支撑元件,对扭矩变化不敏感,其获取瞬时角速度(instantaneous angular speed, IAS)含有的故障信息较齿轮更微弱,因此,利用编码器信号提取滚动轴承故障特征存在诸多困难。为解决该问题,近年来国内外学者开展了基于编码器信号的滚动轴承故障特征提取研究, Renaudin等[2]开展了基于IAS信号的滚动轴承故障特征提取研究,证明了轴承点蚀等局部故障会引起IAS的微小波动;Moustafa等[3]测试了不同故障尺寸、不同负载、不同转速等工况轴承的IAS信号敏感性,结果表明速度越低、负载越大IAS信号提取故障特征效果越好;Gomez等[4]构建深沟球轴承局部故障IAS模型,从动力学角度揭示故障引起的IAS扰动。但目前基于IAS信号的滚动轴承故障检测相关的研究尚处于起步阶段,研究有效的滚动轴承故障检测方法具有重要的应用前景。
滚动轴承故障信息通常淹没在背景噪声和强干扰部件(如齿轮)信号下,且滚动元件具有随机滑动,导致故障轴承信号具有非平稳性[5],增加了滚动轴承故障特征提取的难度。包络分析是轴承故障特征提取有效的方法之一,其核心是准确找到包含故障信息丰富的解调频带[6]。然而在信噪比低的工况下,传统包络分析往往难以找到合适的解调频带。
近年来,循环平稳分析成为滚动轴承故障特征提取的新途径之一。Antoni等[7-9]先研究了循环平稳分析对轴承故障特征的提取,并证明了平方包络谱与循环谱相干(cyclic spectral coherence, CSCoh)的联系;然后研究了旋转机械信号的循环平稳过程模型,论述了滚动轴承的循环平稳特征,证明了循环平稳过程与角度直接相关;提出了循环谱相关算法(cyclic spectral correlation, CSC),为进一步突出故障特征,提出了改进包络谱(improved envelope spectrum, IES),增强了轴承故障的检测效果。但其没有确定优化解调频带的选取准则,若进行全频带积分会引入较多干扰,影响故障特征频率的提取。
为了解决IES积分频带选择的问题,Mauricio等[10]提出了特征优化图IES算法(improved envelope spectrum via feature optimisation-gram, IESFOgram)引入1/3-二叉树对CSC进行解调,选取故障信息丰富的频带,沿谱频率积分获得IES,增强了故障特征的可识别性。Mauricio等[11]考虑到轴承故障可能分布在多个频带,基于IESFOgram提出了组合改进包络谱。然而,上述算法未考虑轴承的随机滑移,当随机滑移存在时,理论特征频率与实际特征频率存在差异,原IESFOgram 算法无法获取信噪比最高时所对应的解调频带。本课题组将随机滑移的影响考虑到诊断特征(diagnostic feature, DF)指标中,完善了IESFOgram算法[12]。然而,上述算法在频带划分时均采用1/3-二叉树频带划分方式,划分频带固定,可能使得到的带宽和中心频率并非最优,随着频带细分可能会导致频带内故障信息丢失,且无法根据信号特征自适应划分频带。同时,1/3-二叉树频带划分增加了计算量。
针对上述问题,结合自适应频带划分算法可根据信号特点采用非均匀带宽自适应划分频带和保留故障信息最大化的优势,研究中提出一种基于改进DF指标的自适应CSC优化解调频带选取算法。首先利用向前差分估计IAS信号;其次用CSC获得故障轴承的双变量谱,并沿着谱频率切片积分得到子频带IES;计算子频带IES的DF数值得到DF曲线,并利用子频带合并频带划分得到优化解调频带;最后,通过包络分析提取滚动轴承故障特征。研究中通过与包络分析、CSCoh双变量谱的包络分析和IESFOgram算法对比验证了所提方法的有效性及优势。
1 基础理论知识简介
1.1 Fast-SC算法
对于具有二阶循环平稳特性的信号x(t),其循环谱相关CSC函数可表示为
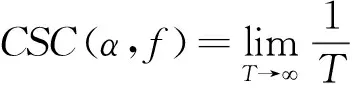
(1)
式中:f为载波频率;α为循环频率;T为循环周期;τ为时延;FFT[·]为快速傅里叶变换;[·]*为共轭;E{·}为数学期望。为了削弱噪声分布不均匀对CSC的影响,对CSC进行归一化处理得到循环谱相干CSCoh函数,表示为
(2)
将CSCoh沿着频率轴进行积分可以得到循环频率的IES,可表示为
(3)
式中:|·|为取绝对值;F2为上限频率;F1为下限频率。与平方包络谱相比IES可以提高循环平稳故障信号的检测,IES对故障的检测能力关键取决于积分频带的选取。若选取的积分频带具有丰富的故障信息,则可以有效提取故障特征,相反,若选取的积分频带存在较多干扰,则会影响故障特征的提取。
1.2 DF指标
DF指标可用于评价划分后频带内故障信息丰富程度,DF数值越大,故障信息越丰富,选定DF最大的频带为解调频带。DF指标为故障特征频率(或故障特征阶次)谐波频率(k·αfault)与边带(2·fb)积分累和的比值。可表示为
DF(fc,bw)=
(4)
式中:fc为中心频率;bw为各子频带带宽;Δf1=fb-fdelta,fb为谐波周围的积分带宽,fdelta为故障特征阶次容差率;αfault为理论故障特征频率。
1.3 子频带合并频带划分算法
为避免故障信息丢失造成故障特征提取时故障特征分量谱线不占优的问题,文献[13]将故障信息最大化作为目标,提出一种自适应频带划分算法。子频带合并频带划分算法包含设定初始子频带的带宽和子频带合并原则两个部分。初始子频带的构造与叠加如图1所示,初始子频带的设定如图1(a)所示。子频带向右滑移可表示为

图1 子频带合并示意图Fig.1 Window function merging diagram
Tnaw[m]=w[m-na]
(5)
式中:w[·]为初始子频带带宽;n为滑移次数;a为滑移距离。子频带叠加如图1(b)所示。子频带合并时首先尝试将第一个子频带与第二个子频带进行合并,如果合并后子频带较合并前子频带DF值更大则保留合并,并尝试合并后面更多的窗口,否则保留第一个子频带;随后,尝试合并第二个子频带和第三个子频带,重复上述过程直至结束。合并后子频带的中心频率和带宽表示为fci和Bfi,如图1所示。
当合并后子频带优于合并前子频带,子频带叠加认为是有效叠加,可表示为
DFxwl≥max{DFxwr,DFxwTl}
(6)
式中,下标wl,wr,wTl分别为合并后子频带、选定子频带和相连子频带。子频带合并频带划分以最大化带宽为目标函数,使提取频带具有最大可能的故障特征频率覆盖范围。最终合并子频带可表示为
(7)
式中:xopt为优化解调频带;Nm为合并后子频带个数。
2 基于CSC的编码器信号滚动轴承故障检测
为实现基于IAS信号的滚动轴承故障特征有效提取,本文提出一种基于DF指标的CSC优化解调频带选取算法,其技术路线如图2所示。其主要步骤如下:

图2 基于CSC的编码器信号滚动轴承故障检测Fig.2 Fault detection of rolling bearings based on the CSC of encoder signals
步骤1利用增量式光编码器获取带有故障信息的编码器信号,并利用向前差分得到滚动轴承IAS信号,向前差分法可表示为
(8)
式中:θi为原始编码器信号;Δti为连续两个编码脉冲之间的时间间隔;v(θi)为在绝对角度θi处的IAS;
步骤2利用式(1)和式(2)提取滚动轴承故障特征相关分量,并在CSCoh中沿循环频率用设定好的带宽得到子频带,并用式(3)计算子频带的IES;
步骤3基于式(4)计算个子频带IES的DF值,得到谱频率的DF曲线;并设定初始子频带为Δf=fs/2Nw,其中fs表示采样频率,研究中fs=5 000×,Nw表示窗长,本文选用窗长Nw=64,因此,Δf= 39.1×,按照式(6)和式(7)对DF曲线进行子频带合并;
步骤4计算合并后子频带内各子频带DF之和,可表示为
(9)
式中:ri(u)为合并子频带内子频带;j为子频带的检索;DFri(u)[xw]为合并子频带内子频带的DF数值。
步骤5选取DF值最大的频带为优化解调频带,包络分析提取故障特征。
3 仿真分析
3.1 试验说明
为了验证所提方法的有效性,建立了轴承故障仿真信号。参照文献[14]齿轮扭振信号与啮合时的振动信号相似,且考虑到轴承IAS信号的仿真模型有待完善。因此,本研究参照振动信号建立轴承外圈点蚀故障仿真模型,可表示为
(10)
式中:T为故障冲击对应的周期;s(t)为点蚀故障引起的冲击震荡;Δti为轴承故障1%~2%的随机滑移;fn为固有频率,fn1=600×,fn2=1 250×;n(t)为零均值的随机白噪声;B为阻尼衰减因子。
仿真设定编码器线数N=5 000,轴承故障特征阶次Oout=5.2×,干扰信号阶次Or=1×,固有频率为fn=500×,故障周期的随机滑移量为Δt=0.01T。
3.2 特征提取
仿真时域波形如图3(a)所示,其包络谱如图3(b)所示。包络谱2×、3×被噪声淹没,故障特征阶次被噪声淹没,辨识困难。

图3 仿真信号时域波形及包络谱Fig.3 Simulating the time domain waveform and envelope spectrum of the signal
利用循环谱相干处理信号如图4(a)所示,包络谱如图4(b)所示。CSCoh双变量谱中背景噪声及干扰成分较强,故障对应特征阶次不易准确辨识。

图4 Fast-SC双谱图及包络谱Fig.4 Fast-SC and full-band integral envelope spectrum
用IESFOgram处理仿真信号,优化解调频带(Oc= 605.5×,bw=39.1×),如图5(a)所示,其IES如图5(b)所示。受到背景噪声干扰,Oout的2×谱线并不显著。

图5 IESFOgram及改进包络谱Fig.5 IESFOgram and improved envelope spectrum
利用基于DF指标的CSC优化解调频带选取算法处理仿真信号结果,如图6(a)所示,其中子频带带宽Δf=39.1×。由式(9)计算获得优化解调频带(Oc= 1191.4×,bw= 351.6×),解调的IES如图6(b)所示。对比图3(b)、图4(b)、图5(b)和图6(b)所提方法的包络谱中故障特征阶次更明显。为验证所提方法的计算效率,选用CPU为Intel Core i7-6700、运行内存为8 G的计算机处理采样时间长度为20 s的试验信号,对比DF指标的CSC优化解调频带选取算法与IESFOgram算法的计算时间,结果如表1所示。

表1 计算时间对比Tab.1 Time of calculating
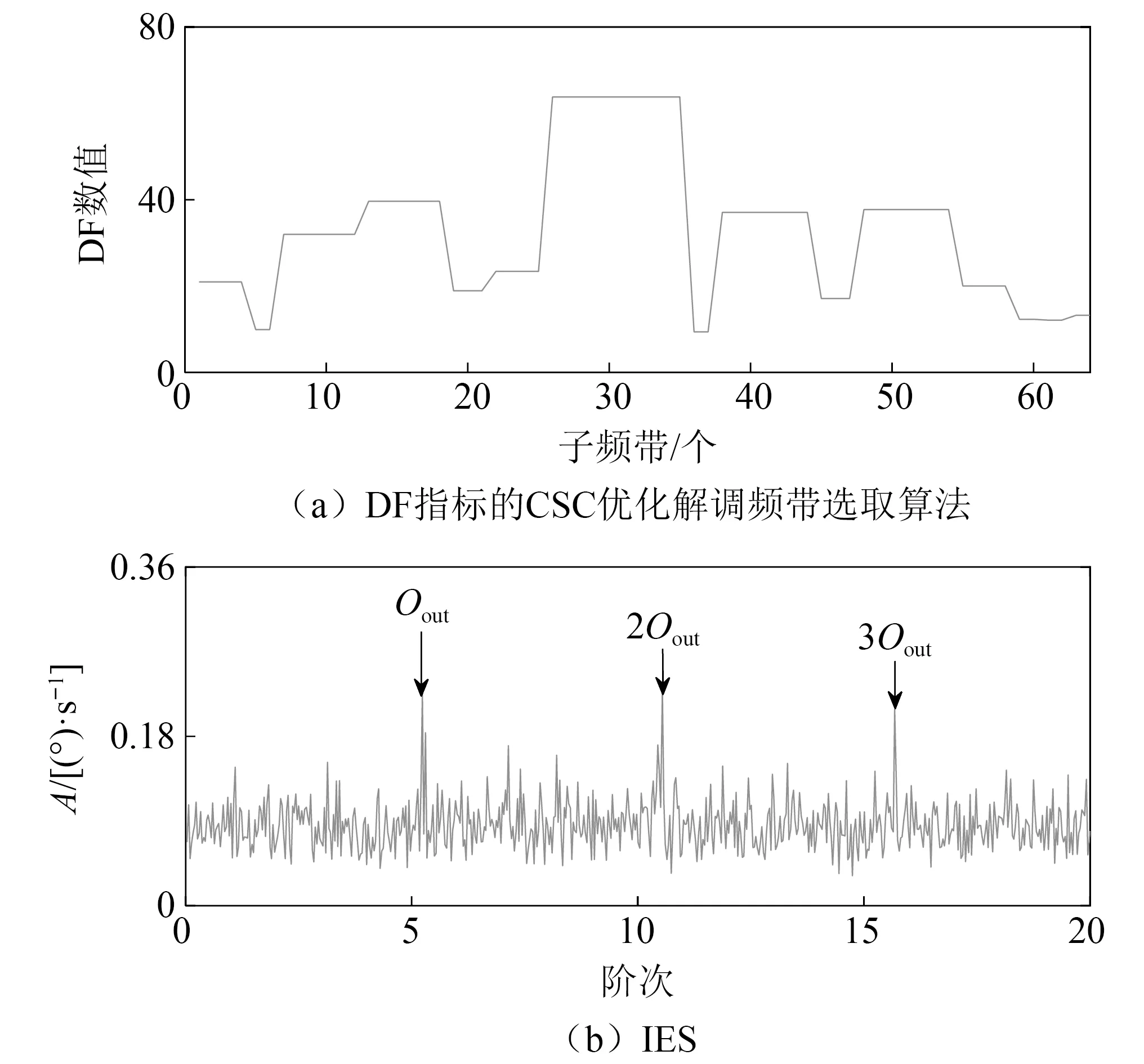
图6 本文所提算法及改进包络谱Fig.6 Algorithm proposed in this paper and improved envelope spectrum
从表1可知,所提基于DF指标的CSC优化解调频带选取算法计算效率较IESFOgram算法高。对比图5(b)和图6(b),本文所提方法IES故障特征频率辨识性较好。
4 试验验证
4.1 试验说明
研究中通过滚动轴承故障试验台验证所提方法有效性。试验台主要包括电机、支撑轴承、径向加载转置、故障轴承、编码器和磁粉制动器六个部分,如图7所示。试验用计数频率为10 MHz的高速计数器获取编码器信号。

图7 试验台Fig.7 Experimental bench
研究中采用苏州广乐公司的光栅式编码器,型号为 SZGLK9040G2,线数为 5 000 线,输出方式为 TTL 信号。试验研究对象为NU206型滚动轴承,节圆直径D=46 mm,滚动体直径d=9 mm,滚动体个数n=13,接触角β=0°。模拟故障轴承外圈用线切割加工有宽度约为1 mm,深度约为0.5 mm的小槽,如图8所示。轴承外圈理论故障特征频率计算可表示为

图8 模拟故障轴承Fig.8 Simulating a faulty bearing
(11)
式中,Or为转频。由上述参数和式(11)计算得到外圈故障特征阶次为5.2×,转频为1×。
4.2 特征提取
通过高速计数器获得的编码器信号如图9所示。

图9 原始编码器信号Fig.9 Original encoder signal
由式(8)获得其IAS信号如图10(a)所示,其包络谱如图10(b)所示。轴承故障相关阶次并不突出,干扰谱线影响特征谱线辨识。

图10 IAS信号及包络谱Fig.10 IAS signal and envelope spectrum
利用循环谱相干处理信号如图11(a)所示,包络谱如图11(b)所示。包络谱中引入干扰成分致使故障特征阶次不易辨识。采用IESFOgram算法对IAS进行处理,优化解调频带(Oc= 19.5×,bw= 39.1×),如图12(a)所示,其IES如图12(b)所示。IESFOgram算法解调的IES故障阶次较包络谱和CSCoh的包络谱故障特征谱线能量占比量更高。然而,其特征阶次受干扰谱线影响不易辨识。
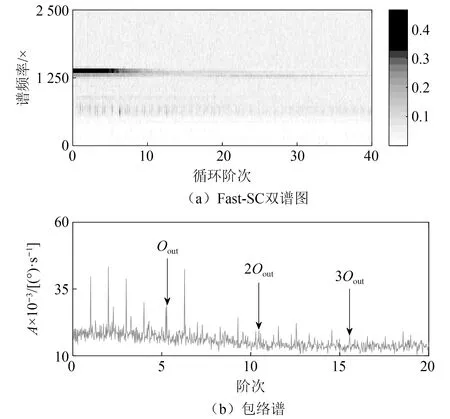
图11 Fast-SC双谱图及包络谱Fig.11 Fast-SC and full-band integral envelope spectrum
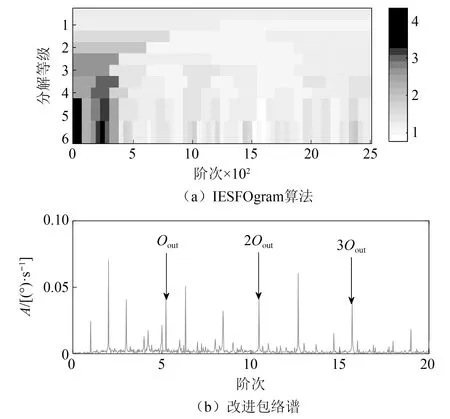
图12 IESFOgram及改进包络谱Fig.12 IESFOgram and improved envelope spectrum
利用Mauricio所提方法处理IAS信号得到组合IESFOgram如图13(a)所示,组合改进包络谱如图13(b)所示。图13(b)中可辨识1×和2×故障特征,但故障阶次周围存在较多干扰,3×故障特征无法有效辨识。

图13 Mauricio所提方法及组合改进包络谱Fig.13 Method proposed by Mauricio and combined improved envelope spectrum
本文所提方法处理如图14(a)所示,其中子频带带宽Δf=39.1×,优化解调频带(Oc= 332.0×,bw= 351.6×),IES如图14(b)所示。对比图10(b)、图11(b)、图12(b)、图13(b)和图14(b)所提方法的包络谱中故障特征阶次较明显。

图14 本文所提算法及改进包络谱Fig.14 Algorithm in this paper and improved envelope spectrum
5 结 论
本文提出了一种基于循环谱相关的编码器信号滚动轴承故障检测方法,通过仿真和轴承实测数据验证了本文所提方法的有效性。所提方法在基于编码器信号的滚动轴承故障特征提取中具有以下优势:
(1)基于DF指标实现CSC解调频带的优化选取,故障特征提取效果优于传统方算法。
(2)较已有的IESFOgram算法,计算效率较高。
