Vibrational resonance in globally coupled bistable systems under the noise background

Jiangling Liu(刘江令), Chaorun Li(李朝润), Hailing Gao(高海玲), and Luchun Du(杜鲁春),†

1Department of Physics,Yunnan University,Kunming 650500,China

2Graduate School,Yunnan Normal University,Kunming 650500,China

Keywords: vibrational resonance,globally coupled bistable systems,power spectral amplification,noise

1.Introduction

Vibrational resonance(VR)[1,2]is another important nonlinear phenomenon after stochastic resonance(SR).[3–5]Both the VR and the SR have important applications in detection of weak signals.[6–9]The core idea of VR is to replace the role of noise in SR with a high-frequency signal.For the reason why high-frequency signals are more convenient to control than noises and there is widespread existence of dualfrequency signals in nature, research of VR has expanded from bistable systems to monostable,[10]multistable,[11–14]asymmetric,[15–17]and other nonlinear systems.[18–21]In addition,VRs with effects of geometric spatial confinement and effects of quantum have also been studied, corresponding to entropic vibrational resonance[22,23]and quantum vibrational resonance,[24,25]respectively.Influence of damping coefficient on vibrational resonance has also been studied by nonlinear analog circuit experiments.[26]In the last few years,machine learning and related methods have been applied to research of stochastic resonance,and achieved good results and progress.[27,28]

Furthermore, it is reasonable to consider interaction between particles or subsystems in practical systems.These coupling effects have a profound impact on dynamic properties of nonlinear systems.[29–31]Specific examples include competing independent synchronous clusters,[30]system size synchronization,[31]and so on.Furthermore,SR[13,32–34]and VR[11,35,36]in coupled nonlinear systems have been extensively investigated.Influence of coupling strength and system size on resonance behavior of a coupled system will have an optimal value.[37,38]On the other hand, stochastic perturbations are inevitable in natural and artificial systems,so it is natural to consider coupled VR with noises.Inspired by the constructive effect of noise in stochastic resonance,we are interested in the interaction between vibrational resonance and stochastic resonance in globally coupled bistable systems.To our best knowledge,the vibrational resonance in noisy bistable systems with global coupling is hardly investigated, which is an issue we will investigate in this work.

This paper is arranged as follows.In Section 2, we introduce the basic model and methods described by Langevin equations.The main results and detailed analysis are presented in Section 3.The conclusions are given in Section 4.

2.Model and methods

A globally coupled bistable system driven by two harmonic signals and noise is described by the following Langevin equations:

wherexiis the position of the particle, andεis the coupling strength,Nis the number of identical bistable units,andξi(t) is Gaussian white noise with autocorrelation functions〈ξi(t)ξj(t′)〉=δijδ(t −t′).AandωLare the amplitude and frequency of the low-frequency signal,respectively,BandΩHare the amplitude and frequency of the high-frequency signal,respectively,andDis the noise intensity.

According to Eq.(1), the time series of the mean-field with different amplitudesBof the high-frequency signal obtained by stochastic simulation is shown in Fig.1.The initial value of each oscillator in the system is randomly±1 with equal probability.With the appropriate amplitude of the highfrequency signal,the time series of the mean-field will switch between the two equilibrium points at the frequencyωLof the weak low-frequency signal.This is due to the fact that the high-frequency signal can change the equilibrium point and the effective stiffness of the bistable system.[2]The highfrequency signal induces synchronization between the system output and the low-frequency signal,which is similar to effects of noises in the SR.

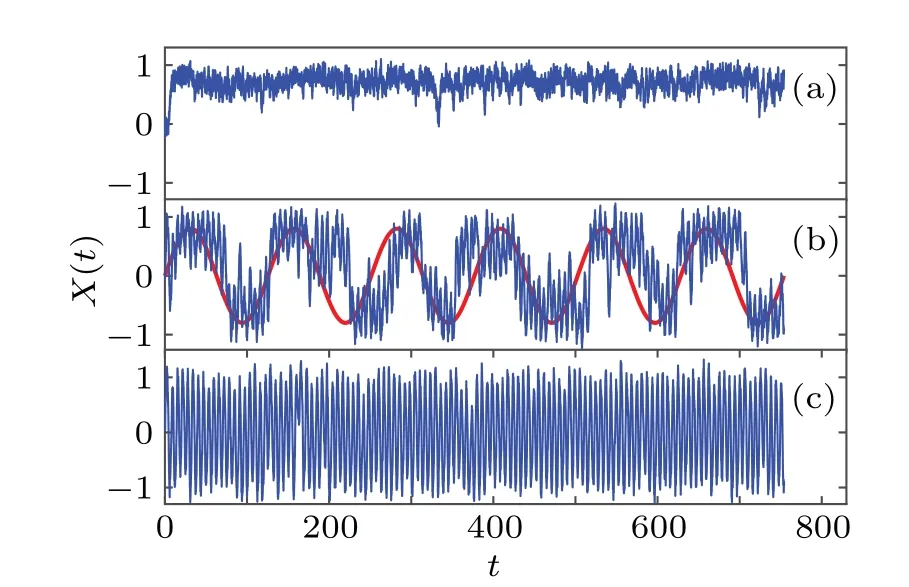
Fig.1.The time series of the mean-field X(t)=N−1 ∑i xi(t)for different amplitudes of the high-frequency signal:(a)B=0,(b)B=0.44,(c)B=0.8.We also depict the low-frequency weak signal (its amplitude is not in scale)to demonstrate the synchrony between the time series of the mean field and the low-frequency signal.Other parameters are set as D=0.7,ε =5.1,N=60,A=0.02,ωL=0.05,and ΩH=1.

Next, using the Gaussian approximation,[38–40]wherexi=X+δi,Eq.(1)can be simplified to

whereX=N−1∑i xi,M=N−1∑i, andΓ(t) is the Gaussian white noise having the same properties asξi(t)in Eq.(1).Eqation (2) shows that the system has two symmetric stable fixed points and one unstable point in the thermodynamic limitN →∞when the two harmonic signals are absent.The value of the two symmetric stable fixed points and the unstable point of the bistable system are=(2−ε+S)/4 andX=0, respectively,where.The dynamical equation and statistical properties of varianceMcan refer to the literature.[38,39]

By employing the slaving principle motions,[38,39]equation(2)can be further simplified to

Then, using a Chebyshev collocation method,[41]the mean-fieldX(t)can be obtained by combining the numerical solutionP(X,t) of the Fokker–Planck equation (4) with the following numerical integration:

whereM1is the first harmonic of〈X(t)〉 at the frequencyωLof the low-frequency signal,the value ofM1is calculated by a fast-Fourier transform.[22]The first method is the main method in this research,which has no restriction on the amplitudeBof the high-frequency signal.

Then, the second method to get PSAηis given, that is, the analytical expression based on the linear response theory.According to the method of direct separation of slow and fast motions,[2,22]one can obtain a coarse-grained version of Eq.(3)as follows:

The third method,i.e.,the stochastic simulation based on the Langevin Eq.(1), has been implemented by the standard stochastic Euler algorithm to verify the rationality and correctness of the first two methods.The number of stochastic trajectories is 2000,and the spin of each stochastic trajectory is 12 times the period of the low-frequency signal, where the time step is 0.001.The mean-field〈X(t)〉 can be obtained by taking the ensemble average of 2000 stochastic trajectories.Then the PSAηcan be obtained by Eq.(7), whereM1is the first harmonic output signal at the frequencyωLof the mean-field〈X(t)〉.

3.Results and discussion

The variation of PSAηwith the amplitudeBof the highfrequency signal obtained by the three different methods is shown in Fig.2.The PSAηobtained by the three methods all exhibit resonance with the increase of the amplitudeBof the high-frequency signal.The numerical solution of the Fokker–Planck equation agrees well with the simulated solution of the Langevin equations,while the analytical solution shows a deviation from the other two solutions.The increase of the amplitudeBof the high-frequency signal will reduce the height of the effective barrier.[1,2]When the height of the effective barrier close or even less than the amplitudeAof the weak signal,the results obtained from the linear response theory will not be applicable.[22]Furthermore,the computation time required for the Fokker–Planck equation is much smaller than the Langevin equations, and the linear response theory imposes strict limits on the amplitudeBof the high-frequency signal to ensure the bistable nature of the system.For the reasons mentioned above,in the following we mainly use the numerical solution method based on the Fokker–Planck equation.

Fig.2.The PSA η versus the amplitude B of the high-frequency signal for the three methods.The line represents the numerical solution based on the Fokker–Planck equation,and the dotted line represents the theoretical results based on Eq.(8),where the symbol represents the result obtained by stochastic simulation according to the Langevin equation.Other parameters are set as D=1,ε=5.5,N=60,A=0.02,ωL=0.05,and ΩH=1.

Considering that the system size tends to vary in the actual coupled system,which has a significant impact on the dynamical properties of the system, the effect of the amplitudeBof the high-frequency signal on the PSAηat different system sizes has been studied,as shown in Fig.3.Only when the number of coupled oscillators is greater than a certain value,will the phenomenon of VR in the system appears.In particular,when the amplitude of the high-frequency signal is zero,the system still resonates with the increase of the system sizes,which is called the system size resonance and has been reported by Pikovskyet al.[38]It should be noted that a larger amplitudeBof the high-frequency signal will eliminate the resonance because the excessively strong amplitudeBof the high-frequency signal will cause the transition of the effective potential function of the system from bistable to monostable.An interesting phenomenon is shown in Fig.3,when the system size is small, the amplitudeBof the high-frequency signal required for the PSAηto realize its maximum value is small.As the system size increases, the amplitude of the high-frequency signal required for the PSAηto realize its maximum value will also increase.The reason for this phenomenon is that if the system size increases, the effective intensity of noise accepted by the cluster of non-linear system will decrease,and the system requires enough energy to realize the state of resonance.Therefore,as the size of the system increases,the amplitude of the high-frequency signal required to realize resonance also increases.

Fig.3.The PSA η versus the system size N and the amplitude B of the high-frequency signal.Other parameters are set as D=1,ε =5.5,A=0.02,ωL=0.05,and ΩH=1.

In a coupled nonlinear system, the effective coupling strength of the mean field will vary with the external excitation parameters,[37]and it is important that the system has a large value of the PSAηunder a large range of coupling strength.The PSAηas a function of coupling strength and system size is shown in Fig.4.For the properly sized system,resonance exists over a wide range of coupling strengths,while for the small-sized system only a weak resonance exists under the condition of strong coupling.This indicates that system size and coupling strength have a significant effect on VR in the globally coupled bistable system.

As mentioned in the introduction, noise is inevitable in natural and artificial systems.The influence of noise on VR has been considered in single bistable systems.[2,42]It is a natural problem to consider whether noise in coupled VR has a similar role similar to that in a couple-free bistable system.Figure 5 shows the PSAηas functions of the noise intensityDand the amplitudeBof the high-frequency signal.It is worth noting that although the noise intensityDor the amplitudeBof the high-frequency signal is small or tends to zero,the system still exhibits resonance phenomena, which correspond to coupled VR[36]and coupled SR.[43]The PSAηwill decrease with the increase of the noise intensityD,and eventually lose its peak structure.The mechanism of this result is that noise injects energy into the system that contributes to all frequencies.[2,22]This weakens the contribution of the high-frequency signal and reduces its weight in the PSAη.On the other hand, the increase of amplitudeBof the highfrequency signal enhances and then eliminates the coupled SR.The increase of the amplitudeBreduces the stiffness of the non-linear system, which is conducive to the occurrence of SR.However, its excessive increase induces the transition of the system from bistable state to monostable state, thus making the system lose the condition of SR.[1,2]In brief, in the globally coupled bistable systems under the noise background,the noise suppresses the beneficial effect of the high-frequency signal on the resonance.The high-frequency signal favors the positive effect of noise on the resonance under the condition of bistable properties of the nonlinear system.

Fig.4.Dependence of the PSA η on the coupling strength and the amplitude B of the high-frequency signal for (a) N =60 and (b) N =25.The parameters are D=1,A=0.02,ωL=0.05,and ΩH=1.

Changes in the noise intensityDand the coupling intensityεcan cause the system to switch between an ordered state and a disordered state.According to Ref.[39](in the absence of an external drive, i.e.,A=0,B=0), the critical values of noise intensity and coupling intensity can be derived to satisfy the transcendental equation

As shown in Fig.6, the premise of our results is a system in an ordered state.In addition, the relationshipε>3Dalways holds so that the system is in a bistable state.[38]On this basis,the high-frequency signal induces the dynamic phase transition from bistable to monostable, which leads to the vibrational resonance.

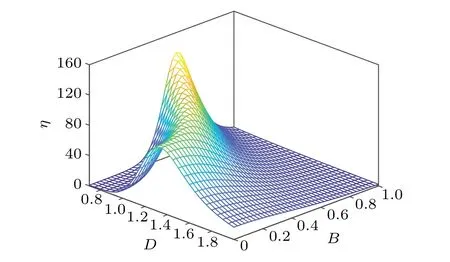
Fig.5.Under the influence of different intensities D of noise,the PSA η dependent on the amplitude B of the high-frequency signal.Other parameters are taken as ε =5.5, N =60, A=0.02, ωL =0.05, andΩH=1.

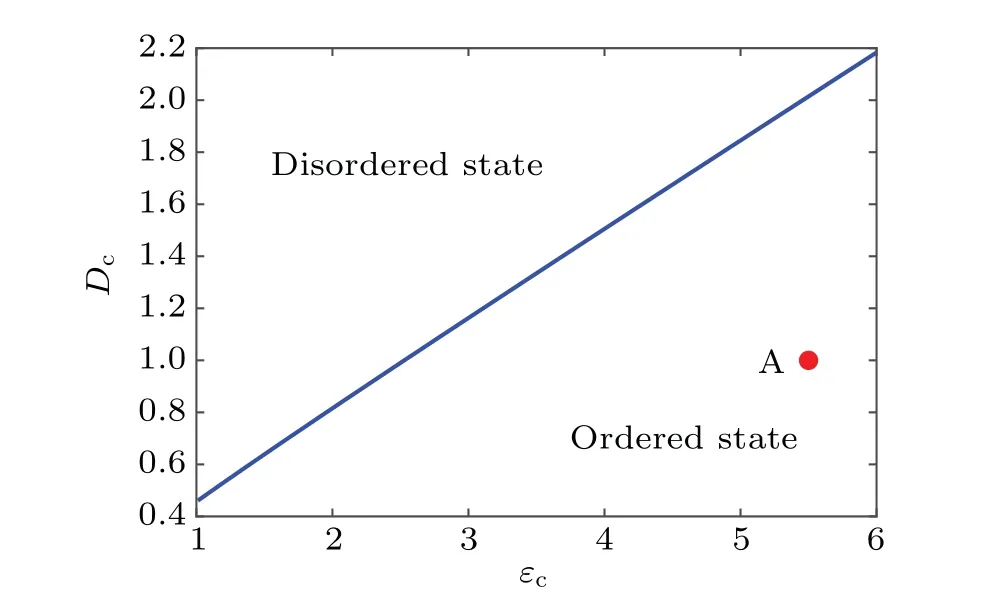
Fig.6.The ordered and disordered states in the model parameter space based on Eq.(9).The coordinate values of point A is the typical parameter values adopted above(ε =5.5,D=1).

4.Conclusions

The phenomenon of vibrational resonance influenced by the system size,coupling strength and noise has been studied in globally coupled bistable elements.The power spectral amplifications are obtained by the linear response theory solution based on the mean-field approximation and the slaving principle,the simulated solution based on the Langevin equations and the numerical solutions based on the Fokker–Planck equation.The three methods all show that the vibrational resonance exists over a wide range of parameter values.The increase in system size induces and enhances the vibrational resonance,while the increase in noise intensity suppresses and eventually eliminates the vibrational resonance.Both the stochastic resonance and the system size resonance can coexist with the vibrational resonance in different parameter regions.Effects of noise on the vibrational resonance are quite different from that of high-frequency signal on the stochastic resonance.Using these properties reasonably and combining the adjustment of other parameters can provide theoretical guidance for detection and extraction of weak signals in noisy multi-stable systems.

Acknowledgements

Project supported by the Xing Dian Talents Support Project of Yunnan Province (Grant No.YNWR-QNBJ-2018-0040), the Youth Project of Applied Basic Research of Yunnan Science (Grant No.202201AU070062), and the Yunnan University’s Research Innovation Fund for Graduate Students(Grant No.KC-22221171).