Elliptically polarized high-order harmonic generation in nitrogen molecules with cross-linearly polarized two-color laser fields

Chunyang Zhai(翟春洋), Yinmeng Wu(吴银梦), Lingling Qin(秦玲玲), Xiang Li(李翔),Luke Shi(史璐珂), Ke Zhang(张可), Shuaijie Kang(康帅杰), Zhengfa Li(李整法),Yingbin Li(李盈傧), Qingbin Tang(汤清彬), and Benhai Yu(余本海)

College of Physics and Electronic Engineering,Xinyang Normal University,Xinyang 464000,China

Keywords: high-order harmonic generation,attosecond pulse,elliptically polarized

1.Introduction

High-order harmonic generation (HHG) is an intriguing nonlinear phenomenon induced by strong light–matter interactions.[1]High-order harmonics generated from the gas target, in particular, have attracted considerable attention in experiments and theory.The mechanism of high-order harmonics generated from gases can be explained by the semiclassical three-step model.[2]First, an electron leaves its parent core by tunneling.Then, the electron is accelerated in the laser field.Finally, when the laser field changes its direction, the electron returns to the parent core emitting highorder harmonics.High-order harmonics span a very broad spectral range and are locked in phase, leading to the generation of attosecond pulses in the extreme ultraviolet and soft x-ray regions.[3–8]In addition, high-order harmonics contain rich information of the atomic and molecular targets, providing a unique way of probing the structure and dynamics of targets.[9–11]In particular, circularly or elliptically polarized high-order harmonics have greater value in numerous applications, such as chiral recognition studies,[12]ultrafast chiral-specific dynamics in molecules,[13]and magnetic circular dichroism spectroscopy.[14,15]According to the semiclassical three-step model, the electron recombines with the parent core along the laser polarization direction when driven by linearly polarized laser fields.As the ellipticity of the driving laser field increases,the harmonic efficiency drops significantly due to the rapid decrease of the electron’s recombination rate.[2,16–18]Therefore, it represents formidable challenges in generating efficient high-order harmonics with high ellipticity at present.

In the past few decades,several schemes have been developed to generate circularly or elliptically polarized high-order harmonics.One method proposes generating elliptically polarized high-order harmonics from prealigned molecules.[19–21]In this scheme,prealigned molecules driven by one-color linearly polarized laser fields can generate high-order harmonics with nonzero ellipticity.However, the ellipticity of the highorder harmonics obtained through this method is too small to synthesize an attosecond pulse with high ellipticity.Another type of method uses two-dimensional driving laser fields.For example,circularly polarized high-order harmonics can be efficiently generated in a bichromatic counter-rotating circularly polarized (BCCP) laser field.[22–30]The BCCP field consists of a circularly polarized fundamental field and its second harmonic (SH) field with opposite rotation directions.According to the selection rule,[31,32]only (3m±1) order harmonics (mis a positive integer) can be obtained in an isotropic target.The (3m+1) order harmonics are circularly polarized with the same helicity as the fundamental field.Conversely, (3m −1) order harmonics present the same helicity as the SH field.As a result, the ellipticity of synthesized attosecond pulses is significantly limited due to the opposite helicities of adjacent order harmonics with considerable intensities.On this basis, noncollinear driving laser fields have also been adopted in producing elliptically polarized HHG.Using the noncollinear driving laser fields,adjacent order harmonics can be directly angularly separated with opposite helicities in the far field.[33,34]However, the noncollinear approach limits the interaction volume of the driving laser with targets,which leads to a decrease in the yield of the harmonics.In recent years, an alternative way of generating elliptically polarized high-order harmonics has also been developed based on the cross-linearly polarized two-color laser fields.[35,37]Theoretically,by adjusting the crossing angle and the relative phase of the cross-linearly polarized two-color laser fields, elliptically polarized high-order harmonics can be generated from atomic gas targets.

In the present work,we investigate the polarization properties of HHG in alignment N2with the cross-linearly polarized two-color laser fields.The spatial structure of the molecules offers more degrees of freedom.By adjusting the molecular alignment angle,as well as the crossing angle,relative phase,and intensity ratio of the driving laser fields,highorder harmonics can be dominantly generated once radiation per optical cycle.Consequently, ellipticity-controllable harmonics with the same helicity can be generated over a wide spectral region.This paves an efficient pathway to generate elliptically polarized attosecond pulses.In addition,an extended comparison shows that the spectral region of harmonics with the same helicity can be controlled and regulated.

2.Theoretical method

In this paper,we calculate high-order harmonic radiation based on the strong-field approximation (SFA) model.[38,39]The time-dependent dipole momentD(t) can be written as(atomic units are used throughout this paper unless otherwise mentioned)[38,40]

wheret′andtare the ionization and recombination time of the electron, respectively.τ=t −t′is the travel time.ξis a positive regularization constant used to eliminate singularities.g(t′) is the ground-state amplitude.E(t) is the laser field.d[ps(t′,t)−A(t′)] andd∗[ps(t′,t)−A(t)] denote the transition dipole matrix element for photoionization and photorecombination process, respectively.A(t) andps(t′,t) are the corresponding vector potential and stationary momentum,which can be written as

S(t′,t)is the quasi-classical action;it can be read as

whereIpis the ionization potential of the target.The harmonic electric field can be obtained by the Fourier transform of the time-dependent dipole accelerationαx,y(t)

whereαx,y(t)=(t).qstands for harmonic order.Ωis the frequency of high-order harmonics.Subscriptsxandydenote the correspondingxandycomponents, respectively.The intensity of the harmonics can be read as

The ellipticity of the harmonics can be expressed as

whereIq,R=|Eq,R|2andIq,L=|Eq,L|2are the right-and leftrotating harmonic intensities,respectively.

3.Results and discussion

In this work, we choose N2as our target molecule to investigate the polarization property of the generated harmonics using cross-linearly polarized two-color laser fields.As shown in Fig.1,the driving laser field consists of a fundamental field(λ=800 nm) and a SH field (λ=400 nm).The fundamental field is polarized along thex-direction.The crossing angle of the polarization directions between the SH and fundamental fields isβ.N2molecule is aligned atαwith the positivex-axis.The electric field of the two-color field is expressed as

whereωis the angular frequency of the fundamental field.EωandE2ωare the amplitudes of fundamental and SH fields,respectively.f(t)is a trapezoidal envelope with a two-cycle rising edge,a two-cycle falling edge,and a six-cycle plateau.In our simulation, the intensity of the fundamental field is fixed atIω=7×1013W/cm2.

Fig.1.Schematic diagram of N2 in the cross-linearly polarized twocolor laser fields.The laser field propagates and is converted to the x–y plane.The fundamental field (red) is polarized along the x direction,and the polarization of the SH field(blue)tilts in relation to the fundamental field at angle β in the x–y plane.The molecular axis of N2 tilts in relation to the fundamental field at angle α in the x–y plane.

Figure 2 presents the high-order harmonic spectra from N2aligned atα=80◦.The intensity ratio between the SH and fundamental fields isI2ω/Iω= 1, the crossing angle isβ=60◦, and the relative phase isϕ=0.Figure 2(a) shows that the intensities of right-and left-rotating polarization components of the harmonics differ greatly.For the harmonics from H19 to H27, the right-rotating polarization components are significantly higher, by one to two orders of magnitude,than the left-rotating polarization components.Therefore,the corresponding ellipticities of the harmonics are large and have the same sign as shown in Fig.2(b).This means that the harmonics are all elliptically polarized and have the same helicity in this wide spectral range near the cutoff region.

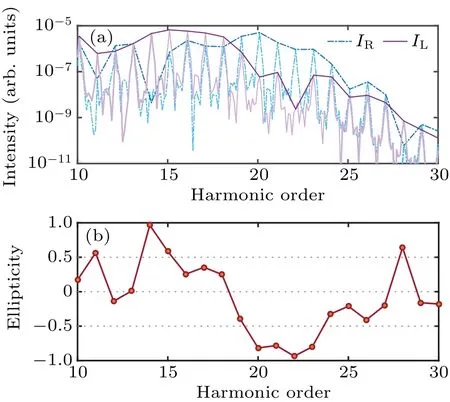
Fig.2.(a)The spectra of the left-(purple solid line)and right-rotating(blue dash-dotted line)harmonic components.(b)The ellipticities as a function of the harmonic order.The intensities of the laser field components are I2ω =Iω =7×1013 W/cm2,the crossing angle is β =60◦,and the relative phase is ϕ =0.The molecular alignment angle is α =80◦.

To obtain a clear physical interpretation of the elliptically polarized harmonics near the cutoff region, we performed the Gabor transform on the intensity and DCP of high-order harmonics[42]

Here we useσ= 1/3ω.Figure 3(a) represents the timefrequency distribution of the harmonic intensity.There are two instances of harmonic radiation per optical cycle.However,the break of the temporal symmetry of the driving laser field leading to the first harmonic radiation being much stronger than the second.As a result,the dominant contribution of harmonics comes from the first radiation.At the same time,one can see that the DCP values of the harmonics from the first radiation are all close to−1 near the cutoff region as shown in Fig.3(b).In combination with Figs.3(a)and 3(b),one can find that only the first radiation is selectively enhanced,its ellipticity is large and it has the same helicity.As a consequence,the harmonics from H19 to H27 exhibit the same helicity in a broad frequency range.These results are consistent with the results in Fig.2.

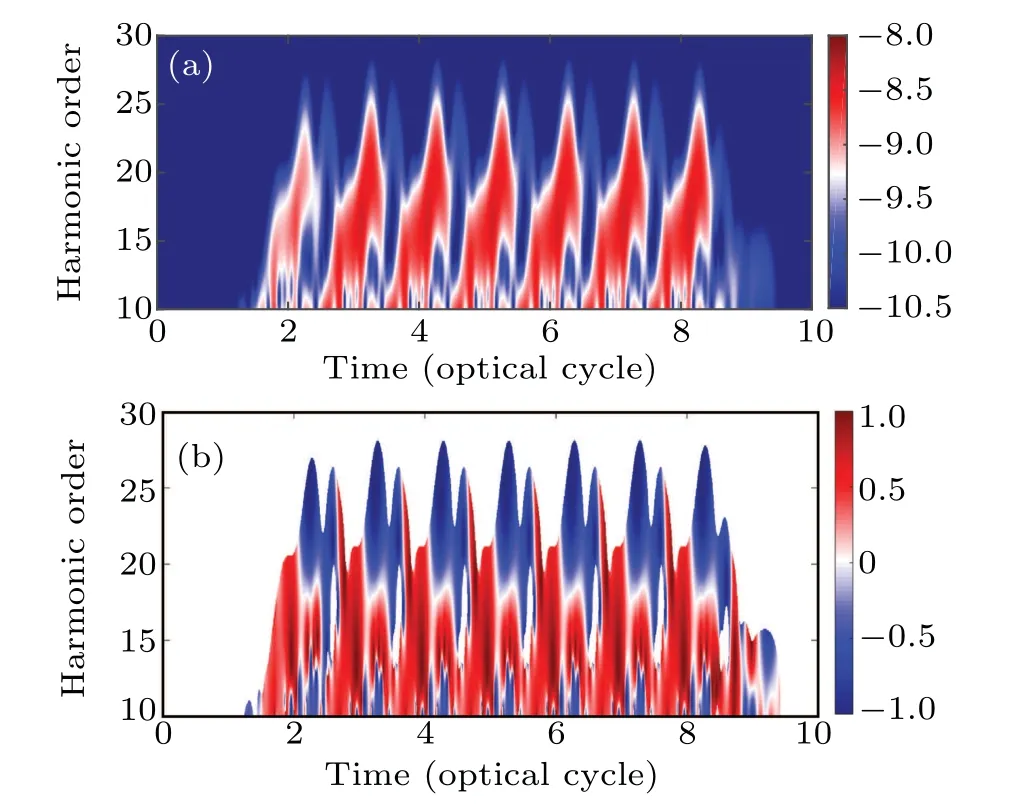
Fig.3.(a)A time-frequency distribution of the HHG under the crosslinearly polarized two-color laser fields.The color map represents the time-frequency distribution in the logarithmic scale.(b) The timefrequency distribution of the harmonic DCP.

In order to characterize the relationship between the ellipticity of high-order harmonics and the target and driving laser parameters, we present the ellipticity distributions with the crossing angle and the molecular alignment angle in Fig.4.Here we fix the intensity ratio toI2ω/Iω=1 and the relative phase isϕ=0.We scanned the crossing angle from 0◦to 90◦with a step of 5◦and the alignment angle from 0◦to 180◦with a step of 5◦.The results show that use of the cross-linearly polarized two-color laser fields is an efficient and robust way to generate elliptically polarized harmonics in a wide range of experimental conditions.As shown in Fig.4,the ellipticity remains large with the same helicity over a wide range of crossing angles,with the alignment angles in the yellow dashed line and the opposite helicity in the black dashed line.It can also be seen that the harmonic ellipticity is not monotonically correlated with the crossing angle and molecular alignment angle.More clearly,one can see that the ellipticity of high-order harmonic distribution varied as the crossing angle and the molecular alignment angle changed in Fig.5.Figure 5(a)shows the distributions of ellipticity with the crossing angle.The molecular alignment angle is fixed atα=80◦.When the crossing angle of the driving field varied from 0◦to 90◦, the ellipticity of the harmonics slowly increased at first; it then reached a maximum when the crossing angle reached about 60◦.The ellipticity gradually decreased with the further increase of the crossing angle.Moreover,the harmonic ellipticity is relatively large, in the range of 45◦to 65◦(between the black arrows in Fig.5(a)).Figure 5(b) shows the distributions of ellipticity with the molecular alignment angle.The crossing angle is fixed atβ=60◦.While the molecular alignment angle varies from 0◦to 180◦, the ellipticity of the harmonics reaches its maximum when the alignment angle is about 80◦.

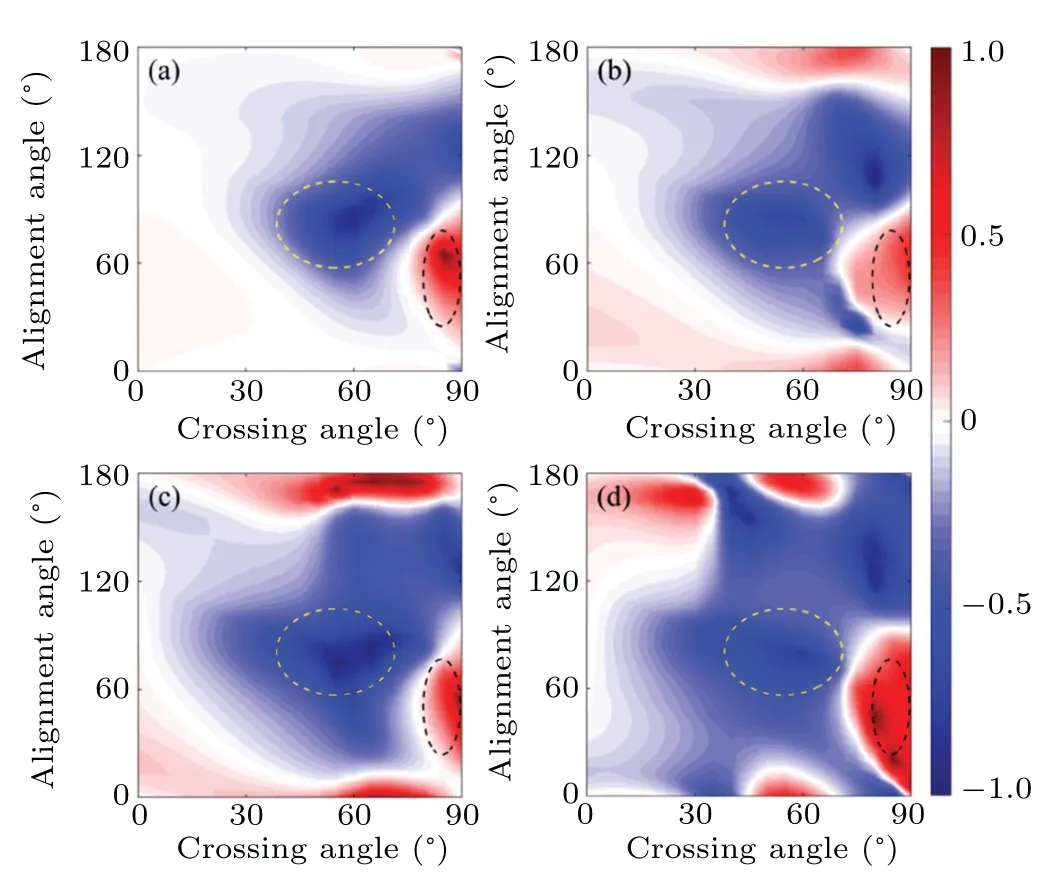
Fig.4.(a)–(d)The ellipticity distributions of the harmonics from H20 to H23 as a function of the crossing angle and the molecular alignment angle.The laser intensity ratio is I2ω/Iω =1 and the relative phase is ϕ =0.

It should be noted that the molecules can only be transiently aligned in the experiment.The high-order harmonic signal measured in the macroscopic molecular ensemble in the laboratory frame is a convolution of the single molecular signal with the alignment distribution.[43,44]To more precisely study the influence of the alignment effect on harmonic ellipticity, we calculate the molecular alignment distribution to exclude ambiguity due to imperfect alignment.In our calculation, we set the alignment degree〈cos2θ〉=0.65, which can be easily achieved in the experiment.[45,46]Then we calculate the results considering the molecular alignment distribution shown in Fig.6.In comparison with the results of perfect molecular alignment, one can see that the dominant contribution of high-order harmonics is still from the right-rotating component in the wide spectral range,although the difference between the left- and right-rotating components has slightly decreased due to the imperfect alignment.The corresponding average value of ellipticity for the harmonics from H19 to H27 dropped by about 0.18.

Fig.5.(a)The ellipticity distributions of the H20 to H23 harmonics as a function of the crossing angle.The laser intensity ratio is I2ω/Iω =1,the relative phase is ϕ =0, and the molecular alignment angle is selected as α =80◦.(b) The ellipticity distributions of the H20 to H23 harmonics are shown as a function of the molecular alignment angle.The crossing angle is β =60◦.

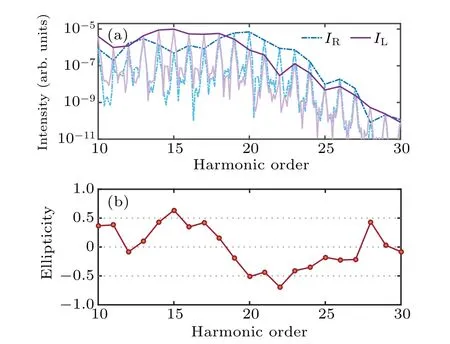
Fig.6.The results considering the molecular alignment distribution.(a)The spectra of the left-(purple solid line)and right-rotating(blue dashdotted line)harmonic components.(b)The ellipticities as a function of the harmonic order.The laser parameters are the same as those in Fig.2.

The results above focus on the dependence of the ellipticity on the molecular alignment angle and the crossing angle.Now,we investigate the influence of the intensity ratioI2ω/Iωand the relative phaseϕof the driving field in Fig.7.We scanned the intensity ratio from 0 to 2 and the relative phase from 0 toπ.The results show that the change of the relative phase of the driving field has a significant effect on both the sign and the magnitude of harmonic ellipticity.While in most conditions,the sign of ellipticity hardly changed as the intensity ratio changed.More clearly,one can see in Fig.8 that the ellipticity of the high-order harmonic distribution varied as the intensity ratio and the relative phase of the driving laser field changed.Figure 8(a)shows the distributions of ellipticity with the relative phase of the driving laser field.The intensity ratio is fixed atI2ω/Iω=1.It can be seen that the ellipticity of the harmonics is periodically controlled by the relative phase with a period ofπ.In addition, the ellipticity of the harmonics reaches a maximum when the relative phase is around 0,π, 2π, etc.Figure 8(b) shows the distributions of ellipticity with the intensity ratio of the driving laser field.The relative phase is fixed atϕ=0.The ellipticity of the harmonics is relatively high when the intensity ratio is around 1.Furthermore,the sign of ellipticity hardly changes when the intensity ratio increases from 0 to 2.

In order to analyze the differences in the influence of the crossing angle,the relative phase,and the intensity ratio on the ellipticity of the harmonics,we focus on the spin angular momentum(SAM)of the driving field.The expression for SAM density is[35]

Owing to the dominant contribution of HHG by the electric field,here we neglect the magnetic field part in the calculation of the SAM density.Then the electric vector potential can be expressed as

We substitute Eqs.(9) and (12) into Eq.(11), and then it can be read as

The results show that the SAM of the cross-linearly polarized two-color laser fields is time-dependent.In the process of high-order harmonic radiation, the photoelectrons ionized at different instants obtain different angular momentums from the driving laser field.Thus, the electrons possess different orbital angular momentums in recollision.According to Refs.[35,36], the ellipticity of the high-order harmonic field is associated with its SAM, which is essentially transferred from the orbital angular momentum of electrons at the moment of recombination.Therefore, the high-order harmonics have time-dependent ellipticity.Equation(13)shows that both the sign and the magnitude of the SAM density varied with the relative phase of the driving field.This is consistent with the results that the relative phase affects both the magnitude and sign of the harmonic ellipticity.It should be noted that the crossing angle and the intensity ratio of the driving laser field affect not only the magnitude of SAM density, but also the recombination time,which also further affects the SAM.

In the above discussion,we focused on the cutoff region of the high-order harmonic spectrum.In addition, by adjusting certain parameters, elliptically polarized high-order harmonics with the same helicity in a large range can also be obtained in the plateau region.For example, when the intensity ratio isI2ω/Iω=0.2, the relative phase isϕ=0.4π, the crossing angle isβ=60◦,and the molecular alignment angle isα=80◦, one can obtain highly elliptically polarized HHG with the same helicity in a broad spectral range in the plateau region.Figure 9(a)presents the harmonic spectra of right-and left-rotating polarized harmonics.The right-rotating components of the harmonics before H18 in the plateau region are stronger than that of the left-rotating components.After H18,there is a reversal of the left- and right-rotating harmonic intensity.Figure 9(b)shows the ellipticity of the harmonics as a function of harmonic order.It can be seen more clearly that the ellipticity of the harmonics is negative in a wide range before H18.That is, elliptically polarized harmonics with the same helicity are generated in a wide spectral range in the plateau region.In addition,the polarization property of high-order harmonics driven by mid-infrared laser fields always holds well.The results indicate that generating elliptically polarized highorder harmonics and controlling their ellipticity with alignment molecules and cross-linearly polarized two-color laser fields could be an effective and robust method.

Fig.9.(a)The spectra of the left-(purple solid line)and right-rotating(blue dash-dotted line) harmonic components.(b) The ellipticities as a function of the harmonic order.The intensity ratio is I2ω/Iω =0.2,the crossing angle is β =60◦,and the relative phase is ϕ =0.4π.The molecular alignment angle is α =80◦.

4.Conclusion

In conclusion, we have theoretically investigated the polarization properties of HHG in N2by using cross-linearly polarized two-color laser fields.By adjusting the crossing angle,the relative phase,the intensity ratio of the driving laser field,and the molecular alignment angle,one can control high-order harmonic emissions that occur only once every cycle of the fundamental pulse.Benefiting from the high ellipticity with the same helicity in each harmonic emission,we obtain elliptically polarized HHG in a broad spectral range.Moreover,the spectral range for the elliptically polarized harmonics can be completely controlled.Hence, the alignment molecules driven by cross-linearly polarized two-color laser fields provide a possible way to generate elliptically polarized attosecond pulses.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant Nos.12104389, 12074329, and 12004323)and the Nanhu Scholars Program for Young Scholars of XYNU.