下承式系杆拱桥地震响应分析
2023-09-05温智泉饶家萁马智慧
温智泉,饶家萁,马智慧
(广西交通设计集团有限公司,广西 南宁 530029)
0 引言
桥梁是公路运输中的重要枢纽,在交通运输中起到至关重要的作用。随着桥梁建设和科学技术的不断发展,出现了多种桥梁结构形式,而拱桥的结构形式较为美观[1-2]。拱桥中的系杆拱桥不仅具有拱桥的基本特征,而且具有自身的独特特点,集拱和梁的优点于一身,将拱和梁有机地结合起来共同承受荷载,充分发挥了梁受弯、拱受压的结构性能,系杆承受拱脚的水平推力,使桥梁结构更加稳定[3-4]。同时由于桥梁结构在地震作用下的损坏程度较为严重,且我国地处地震带,因此对于桥梁结构的地震响应研究成为近年的热点,较多学者对系杆拱桥的抗震性能进行了研究,丁文胜[5]从拱桥自身抗震性能和系杆拱桥与引桥之间的纵向碰撞对结构抗震性能的影响两方面对系杆拱桥的抗震性能进行了研究;陈阶亮[6]依托钱江四桥,分析了系杆拱桥的抗震性能,结果显示,钱江四桥的抗震性能满足设计性能目标;李福万[7]采用有限元分析法,分析了下承式系杆拱桥的抗震性能,并针对拱桥的抗震性能提出建议,成果可为同类型桥梁的抗震设计提供借鉴;方圆等[8]研究了大跨度系杆拱桥纵向、横向采用不同支承体系时的地震响应,并在地震响应的基础上提出了合理的抗震体系;郭恩超[9]采用Midas软件分析了下承式异形系杆拱桥的抗震性能,主要研究了拱桥横向和纵向在地震作用下的响应,结果表明桥梁的各项抗震性能满足要求。由上述文献可知,对于系杆拱桥的抗震性能研究已经较为成熟,但是对于纵向+竖向和横向+竖向地震作用下的系杆拱桥抗震性能的研究并不多见。因此,本文基于上述研究,依托某下承式系杆拱桥,采用Midas软件分析了下承式系杆拱桥在纵向+竖向和横向+竖向地震作用下的响应,研究成果可为同类型桥梁的抗震设计提供参考。
1 有限元模型
作为某公路控制性工程的某下承式系杆拱桥全长100 m,主桥采用80 m的系杆拱桥,拱轴线采用悬链线,拱肋横向间距为32 m。全桥共15对吊杆,均采用桁架单元,拱肋采用矩形钢管混凝土组合材料,管内混凝土采用C60混凝土,中横梁和端横梁均采用C50混凝土材料,拱肋、中横梁和端横梁均采用梁单元模拟,端横梁和拱肋交界点以及端横梁中部采用一般支撑。有限元模型见图1。
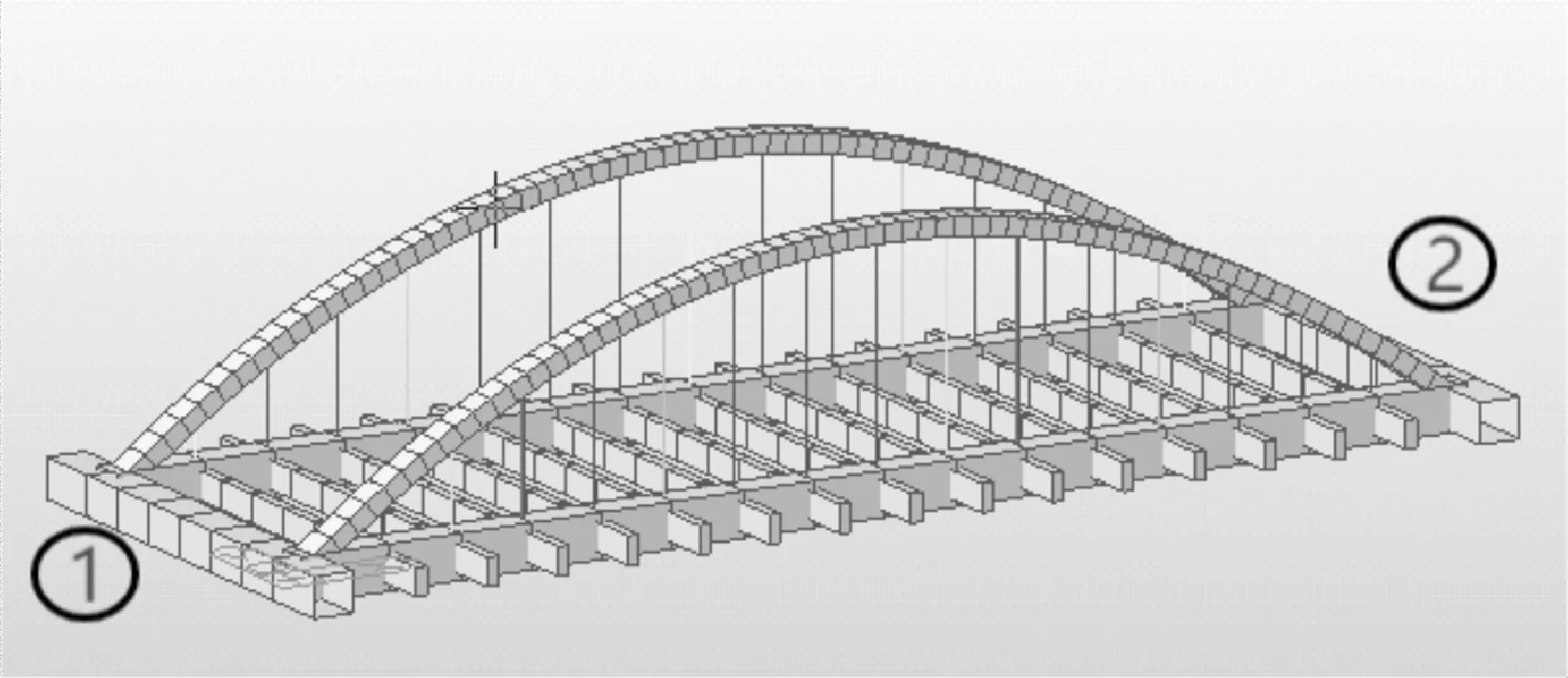
图1 有限元模型图
2 动力特性分析
采用Midas软件分析了系杆拱桥的主桥动力特性,分析结果见下页表1。限于篇幅,仅给出前10阶的自振频率和自振周期,如下页图2所示给出了系杆拱桥的前四阶振型。
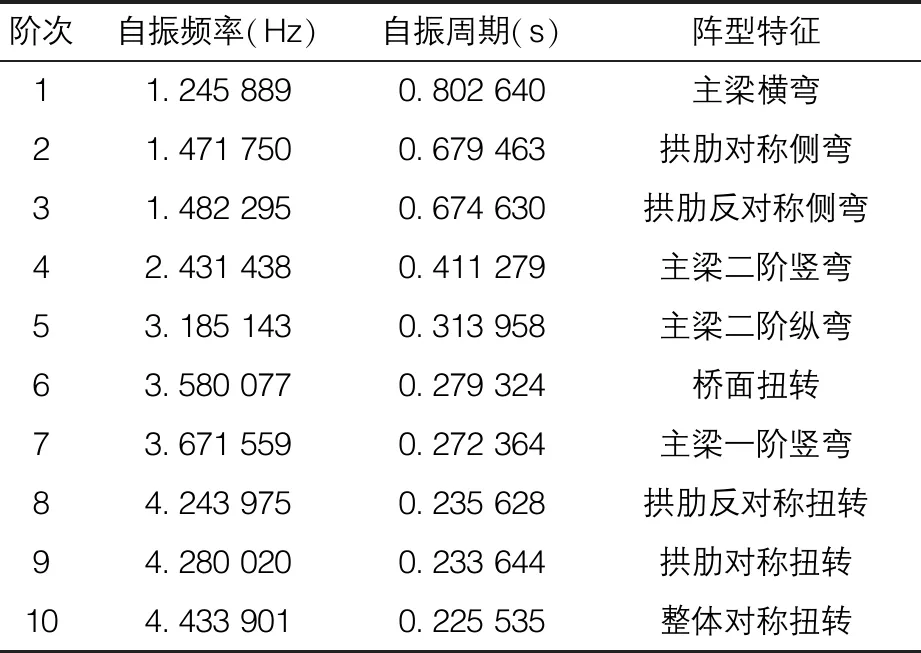
表1 主河槽桥的动力特性分析结果表
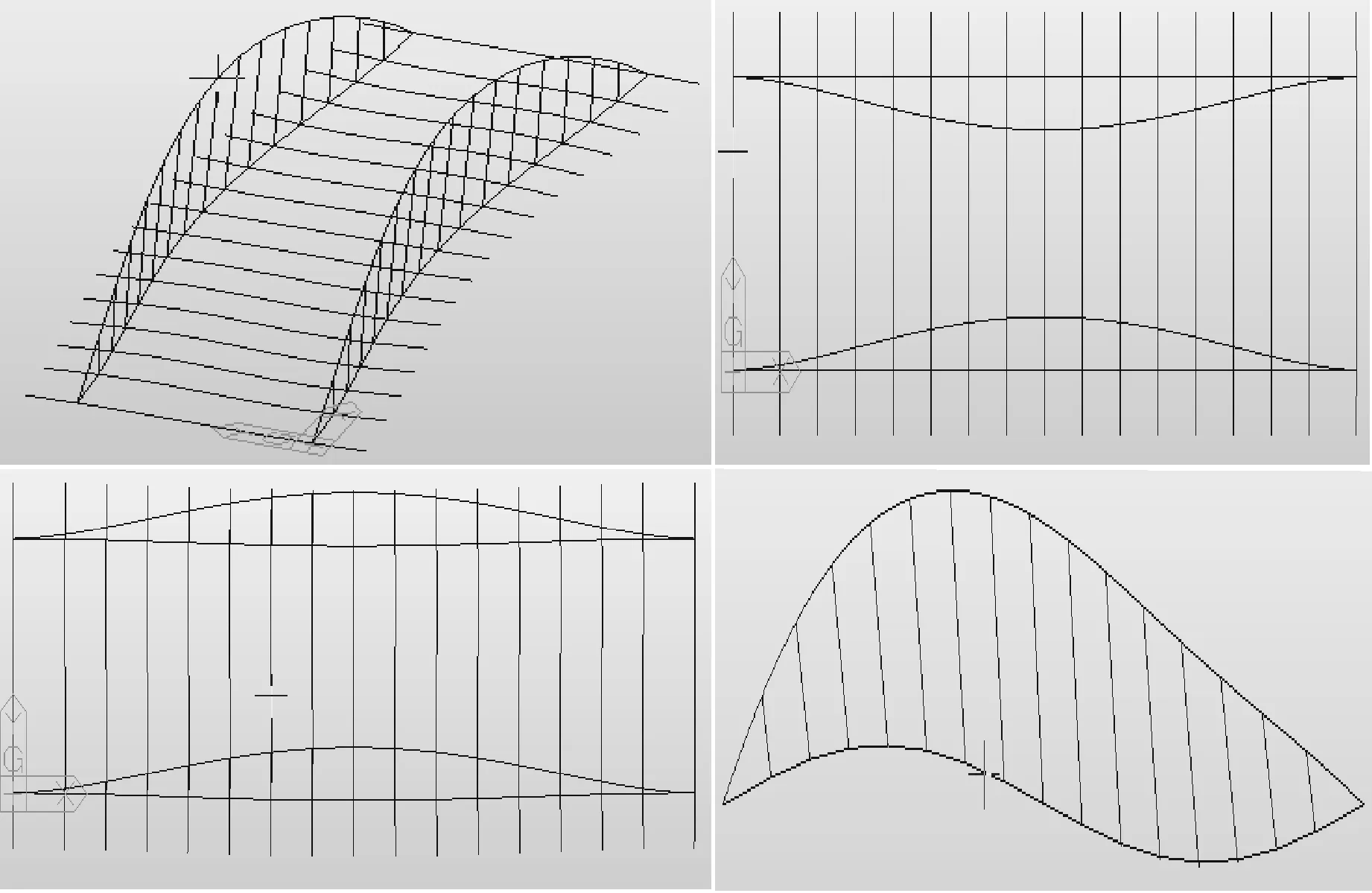
图2 系杆拱桥前四阶振型曲线图
3 反应谱分析
由于该系杆拱桥所处位置的地震基本烈度为6°,场地类别为Ⅲ类,抗震设防类别为B类,根据以上条件以及桥梁抗震设计规范,得到6°区Ⅲ类场地的设计加速度反应谱(见下页图3)。依据反应谱加速度曲线进行计算,主要对纵向+竖向和横向+竖向地震作用下拱肋的内力响应和位移响应进行了分析。
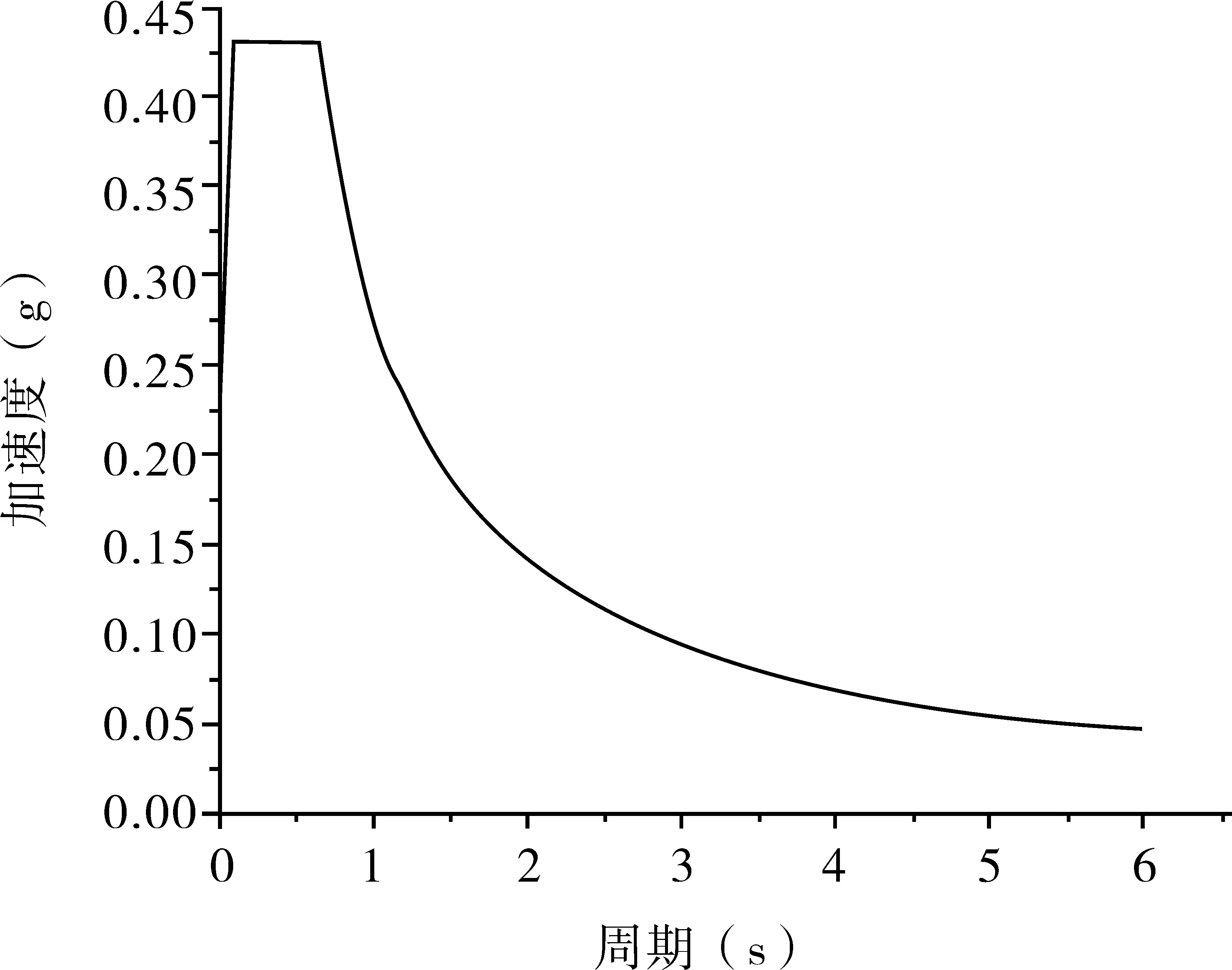
图3 反应谱加速度曲线图
3.1 内力响应分析
地震作用下下承式系杆拱桥拱肋的轴力响应分析结果见图4。由图4可知,在纵向+竖向和横向+竖向地震作用下,拱肋的轴力变化趋势基本相同。在纵向+竖向地震作用下拱肋的轴力远大于横向+竖向地震作用下的拱肋轴力,说明纵向地震+竖向地震作用对系杆拱桥拱肋的影响很大,最大轴力达到3 381.52 kN,为横向+竖向地震作用下拱肋轴力2 358.8 kN的1.4倍。且由图4还可以看出,两种地震作用下拱肋的最大轴力均出现在拱脚位置处,拱肋跨中的轴力最小。故在针对拱肋轴力做抗震设计时,在考虑两种地震作用的同时,还需对纵向+竖向地震作用下的拱肋轴力响应进行特殊计算分析。

图4 轴力响应分析结果曲线图
地震作用下下承式系杆拱桥拱肋的弯矩响应分析结果见图5,地震作用下拱肋弯矩的峰值见表2。由图5可知,纵向+竖向和横向+竖向地震作用下拱肋的弯矩变化曲线基本一致,且地震作用对拱肋的弯矩分布产生了很大影响,弯矩在拱脚、1/4拱肋截面、跨中和3/4拱肋截面均达到峰值,其中跨中位置的弯矩峰值最大,拱肋的弯矩响应受纵向+竖向地震作用的影响较大。

表2 拱肋弯矩峰值表
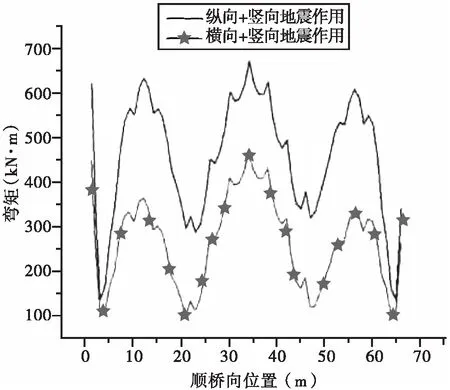
图5 弯矩响应分析结果曲线图
由表2可以看出,纵向+竖向和横向+竖向地震作用下拱肋跨中位置的弯矩均达到最大值,且纵向+竖向地震作用下拱肋各截面(1号拱脚、1/4跨、跨中、3/4跨、2号拱脚)处的弯矩值分别为横向+竖向地震作用下弯矩值的1.38倍、1.74倍、1.43倍、1.8倍、1.29倍,说明横向+竖向地震作用对拱肋的影响较纵向+竖向地震作用弱。由图5和表2可知,在拱桥的抗震设计中,应对两种地震作用进行分析,同时针对纵向+竖向地震作用下拱肋的弯矩响应进行特殊设计分析,其中拱脚位置受力不同可能是由于两端拱脚位置的约束差异引起的。
地震作用下系杆拱拱肋的剪力响应变化见图6。
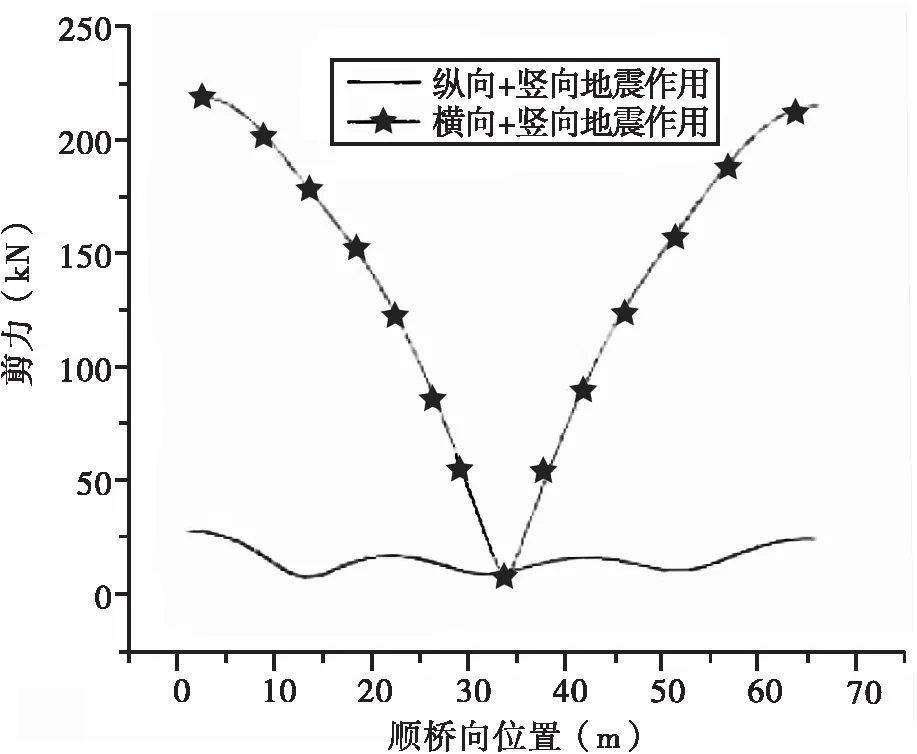
图6 拱肋剪力分析结果曲线图
由图6可知,拱肋的剪力效应主要受横向+竖向地震作用的影响,纵向+竖向地震作用对拱肋剪力效应的影响基本可忽略不计。在抗震设计中,针对拱肋的剪力效应主要考虑横向+竖向地震作用的影响。
3.2 位移响应分析
地震作用下拱顶最大位移值见表3。
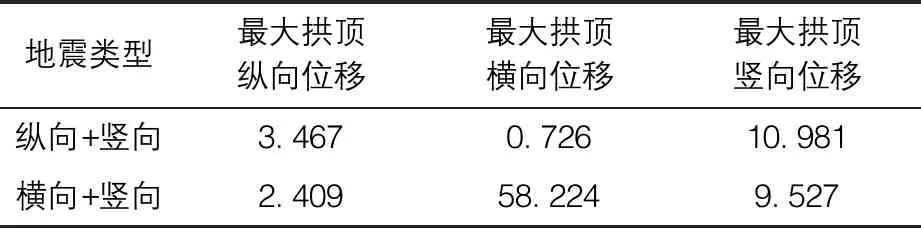
表3 拱顶最大位移值统计表(mm)
由表3可知,纵向+竖向地震作用对拱顶的最大竖向位移影响较大,对拱顶横向位移的影响较小,纵向位移可能是由于受到拱脚的约束作用而比竖向位移小。横向+竖向地震作用下,拱顶的最大横向位移达到58.224 mm,为纵向+竖向地震作用的80.2倍,在地震作用下,要特别注意拱肋的横向位移过大导致桥梁破坏。
4 时程分析结果
4.1 地震动输入
由于该拱桥位于地震高烈度区,因此需要对地震作用下拱桥的结构响应进行研究分析,获取地震作用对拱桥结构响应的影响规律。地震动根据桥梁场地的工程条件,采用Seismomatch软件拟合三条人工地震波。三条地震动的编号分别为B1、B2、B3(见图7)。
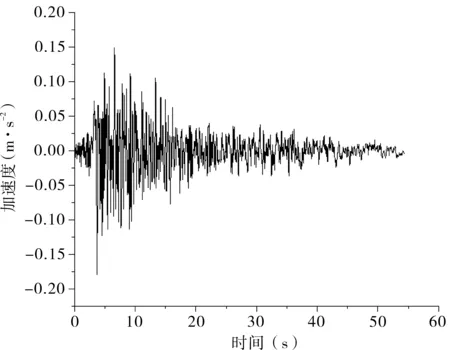
(a)人工地震波B1
4.2 位移时程分析结果
在纵向+竖向地震作用下,系杆拱桥拱顶的横向、竖向和纵向位移分析结果见图8。由图8可知,纵向+竖向地震作用对系杆拱桥拱顶竖向位移响应的影响最大,其次对系杆拱桥拱顶纵向位移响应的影响较大,对系杆拱桥拱顶横向位移的影响最小。系杆拱桥拱顶的最大竖向位移为3.49e-03 m,约为拱顶最大横向位移2.45e-04 m的14倍,拱顶最大纵向位移为2.46e-03 m,约为最大横向位移的10倍。总体上看,纵向+竖向地震作用下系杆拱桥拱顶的横向位移、竖向位移和纵向位移响应均较小,对系杆拱桥的整体影响很小;但从设计安全角度考虑,在抗震设计中不可忽略此地震作用的影响,应对纵向+竖向地震作用下拱顶的位移响应进行强度和位移验算。
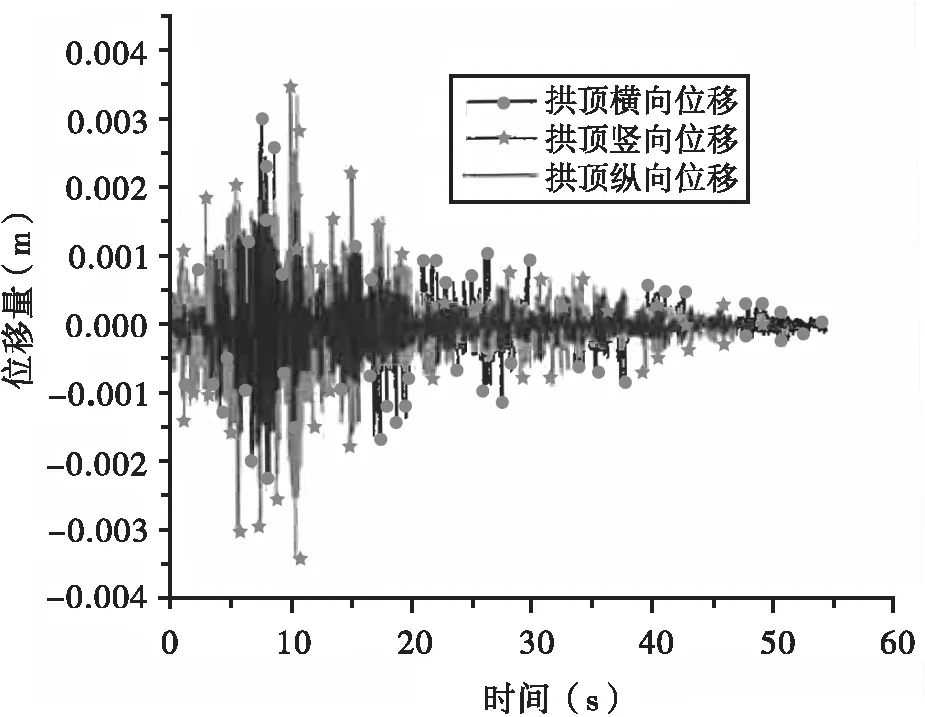
图8 纵向+竖向地震作用下拱顶位移时程曲线图
在横向+竖向地震作用下,系杆拱桥拱顶的横向、竖向和纵向位移分析结果见图9。由图9可知,横向+竖向地震作用对系杆拱桥拱顶横向位移响应的影响很大,拱顶横向位移最大值达到5.55e-02 m,对拱顶的竖向和纵向位移响应影响很小,拱顶竖向位移的最大值为5.34e-03 m,纵向最大位移值为1.32e-03 m。相较于纵向+竖向地震作用对拱桥拱顶位移响应的影响,横向+竖向地震作用的影响更加强烈。因此,为保证系杆拱桥结构的安全,在拱桥的抗震设计中,应从偏安全的角度考虑,对拱桥结构的强度和位移进行验算。
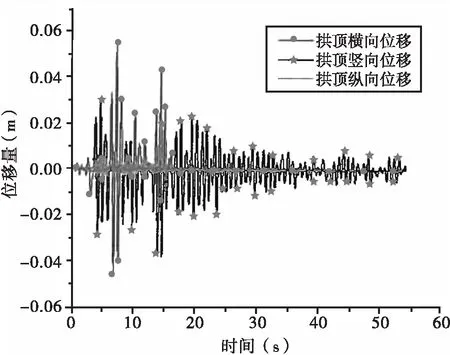
图9 横向+竖向地震作用下拱顶位移时程曲线图
4.3 内力时程分析结果
在纵向+竖向地震作用下,系杆拱桥拱脚和拱肋跨中的轴力分析结果见图10。由图10可知,在纵向+竖向地震作用下,1号拱脚、拱肋跨中和2号拱脚位置的最大轴力响应分别为1.12e+03 kN、9.41e+02 kN和1.18e+03 kN,两个拱脚位置的轴力基本一致,拱肋跨中截面轴力小于两拱脚位置的轴力。尽管有系杆平衡拱脚水平力的作用,但在地震作用下还需注意拱脚位置的轴力,且由于拱桥主要为受压结构,加上系杆对水平力的平衡作用,使拱肋的整体水平力较小,故拱顶位置的轴力较小。由上述分析可知,系杆拱桥的抗震设计从安全角度考虑,应对拱脚位置的轴向力进行验算。
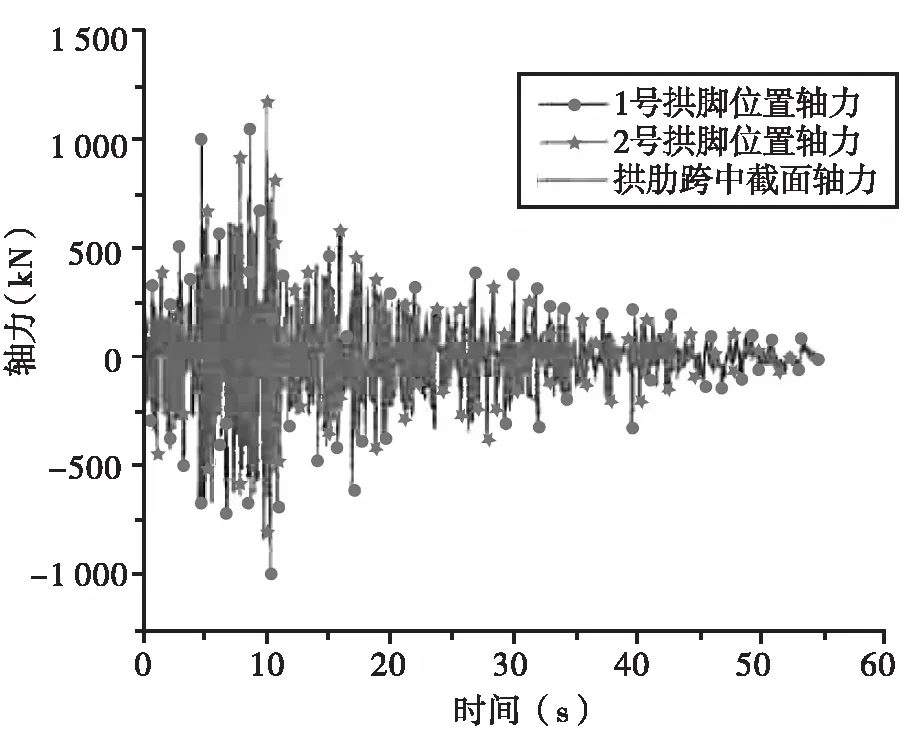
图10 纵向+竖向地震作用下拱肋轴力时程曲线图
在横向+竖向地震作用下,系杆拱桥拱脚和拱肋跨中的轴力分析结果见图11。由图11可知,在横向+竖向地震作用下,1号拱脚、拱肋跨中和2号拱脚位置的最大轴力响应分别为1.54e+03 kN、1.57e+03 kN和1.27e+03 kN。在横向+竖向地震作用下,1号和2号拱脚位置的轴力较纵向+竖向地震作用有所增大,但增幅较小;而横向+竖向地震作用下跨中截面的轴力较纵向+竖向地震作用增幅较大,说明横向+竖向地震作用对系杆拱桥拱肋轴力响应的影响更大,且在横向+竖向地震作用下,两拱脚的轴力基本一致。

图11 横向+竖向地震作用下拱肋轴力时程曲线图
在纵向+竖向地震作用下,系杆拱桥拱脚和拱肋跨中的剪力分析结果见图12。由图12可知,纵向+竖向地震作用下,整体的剪力效应都比较小,最大的剪力值为3.62 kN,整体上该地震作用对系杆拱桥的影响较小。

图12 纵向+竖向地震作用下拱桥剪力时程曲线图
在横向+竖向地震作用下,系杆拱桥拱脚和拱肋跨中的剪力分析结果见图13。由图13可知,横向+竖向地震作用对该系杆拱桥拱肋剪力的影响较大,1号拱脚位置的最大剪力值为176.5 kN,2号拱脚位置的最大剪力值为168.3 kN,拱肋跨中位置的最大剪力为2.5 kN,计算结果符合拱肋主要受压的特征,两拱脚位置的剪力基本一致。与纵向+竖向地震作用相比,横向+竖向地震作用对拱脚位置剪力响应的影响更大。拱肋主要受压,整个拱肋的剪力响应较小。
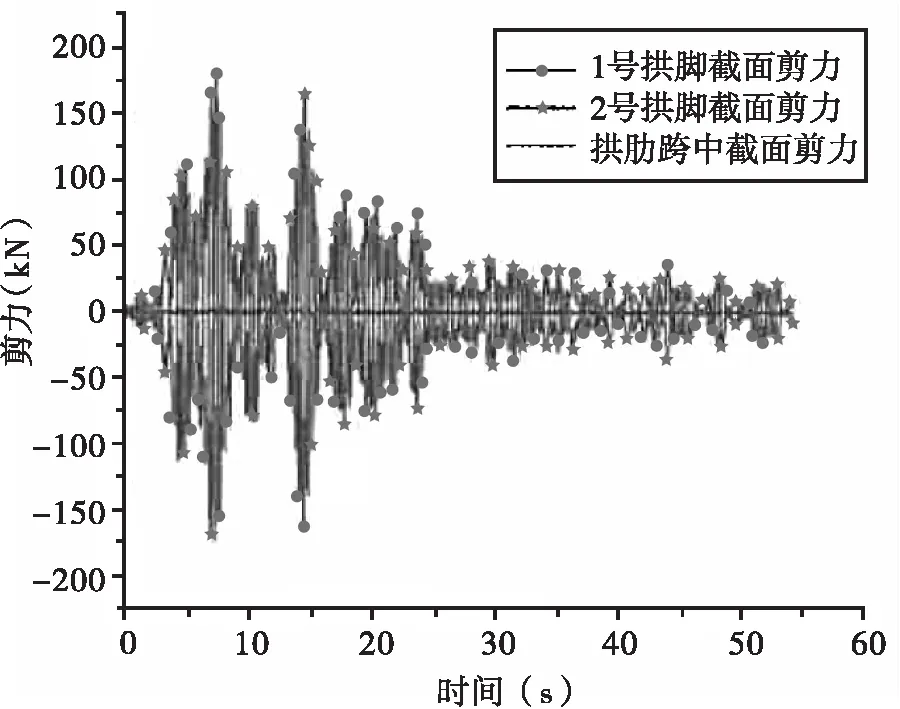
图13 横向+竖向地震作用下拱桥剪力时程曲线图
在纵向+竖向地震作用下,系杆拱桥拱脚和拱肋跨中的弯矩分析结果见图14。由图14可知,1号和2号拱脚位置的最大弯矩分别为40.99 kN·m和35.18 kN·m,跨中截面位置的最大弯矩为15.09 kN·m,最大弯矩<50 kN·m,说明纵向+竖向地震作用对拱桥整体弯矩响应的影响很小。
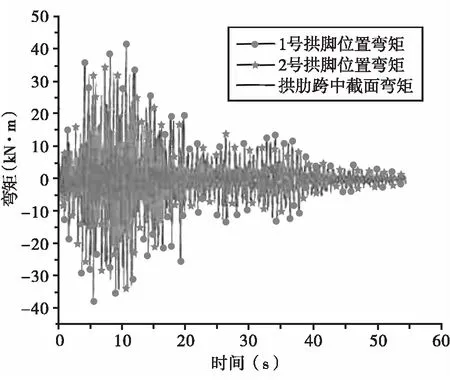
图14 纵向+竖向地震作用下拱桥弯矩时程曲线图
在横向+竖向地震作用下,系杆拱桥拱脚和拱肋跨中的弯矩分析结果见图15。由图15可知,横向+竖向地震作用对该系杆拱桥拱肋弯矩的影响较大,1号和2号拱脚位置的最大弯矩分别达到3 360.7 kN·m和2 968.8 kN·m,跨中截面位置的弯矩也达到了1 407.86 kN·m,说明横向+竖向地震作用对系杆拱桥弯矩响应的影响较大。且与纵向+竖向地震作用相比,横向+竖向地震作用对系杆拱桥弯矩响应的影响更大,在横向+竖向地震作用下拱桥的整体弯矩值大幅度增加。在抗震设计时,要特别注意横向+竖向地震作用对系杆拱桥拱脚位置弯矩的影响。
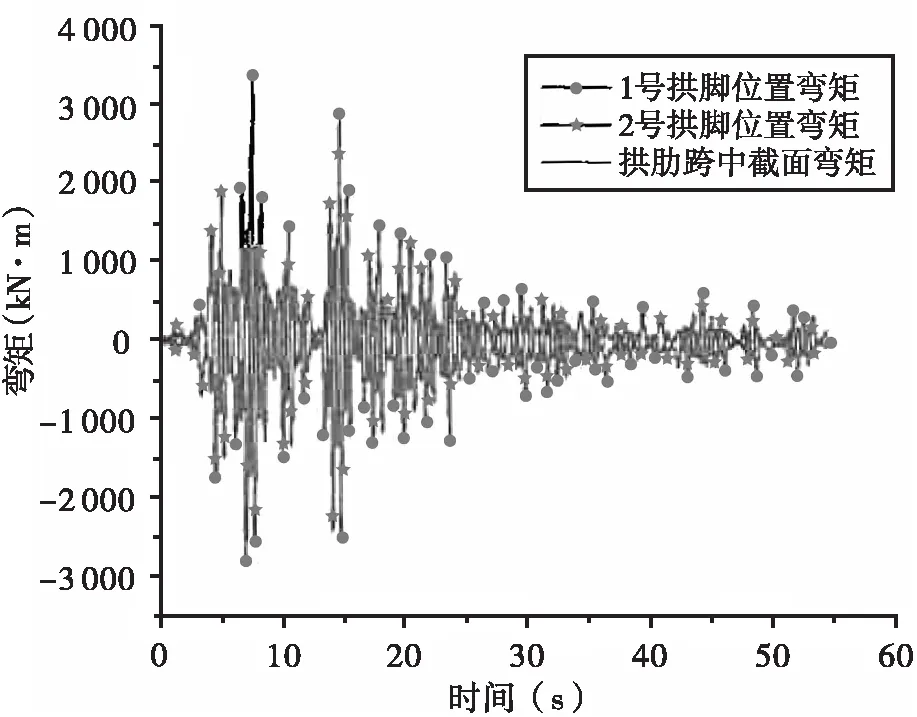
图15 横向+竖向地震作用下拱桥弯矩时程曲线图
5 结语
为研究地震作用下系杆拱桥的响应规律,本文以某公路系杆拱桥为背景,采用有限元法,分析了系杆拱桥在地震作用下的位移和内力响应,主要得出以下结论:
(1)动力特性分析结果显示,拱肋的自振频率值较大,说明系杆拱桥的拱肋(钢管混凝土)具有较大的刚度。
(2)采用反应谱分析法主要分析了纵向+竖向地震作用和横向+竖向地震作用下系杆拱桥的位移和内力响应。结果表明,横向+竖向地震作用对系杆拱桥位移响应的影响比纵向+竖向地震作用的更加明显,而纵向+竖向地震作用下系杆拱桥的内力响应更加明显,在抗震设计时应对两种地震作用做出相应的设计对策。
(3)非线性时程分析结果表明,纵向+竖向和横向+竖向地震作用对系杆拱桥轴力响应的影响差异不大;但横向+竖向地震作用对系杆拱桥位移响应、剪力响应和弯矩响应的影响均更加明显,而纵向+竖向地震作用对拱桥位移、剪力和弯矩响应的影响较弱。整体上看,横向+竖向地震作用对系杆拱桥整体响应的影响更大,对结构的抗震设计不利。
