积分时间对TOF 激光雷达测距误差影响
2023-09-04王炼栋邢昊楠曹明玉
林 昊, 桂 林, 王炼栋, 邢昊楠, 曹明玉
(上海第二工业大学a. 资源与环境工程学院;b. 计算机与信息工程学院;c. 智能制造与控制工程学院,上海 201209)
0 引言
二维成像技术广泛应用于医疗临床诊断、物体无损检测等方面。自动驾驶技术实现的关键在于能否在短距离内以高分辨率查看到障碍物的精确距离和速度,二维成像无法满足上述需求,必须结合场景深度方向上的距离信息,才能有效地还原整个三维场景[1]。目前应用较为广泛的三维成像技术主要包括三角测量法和飞行时间法(time of flight,TOF)两大类。与三角测量法相比,TOF 测距技术具有原理简单、测量快速等优点。同时, 自动驾驶技术对激光雷达技术也提出了更高的要求,低成本、小型化、高精确度都是目前激光雷达技术的主要研究方向。伴随着电子技术和互补金属氧化物半导体(complementary metal oxide semiconductor,CMOS)工艺水平的飞速发展,TOF 测距技术受到越来越广泛的关注。基于TOF 技术的激光雷达具有算法简单、抗干扰能力强、可集成化、稳定性高等优点;且由于采用了主动近红外光照明的方案,TOF 测距系统不受周围环境限制,可在无光照环境下工作;此外,对红外光进行调制解调能够有效地抑制白光的干扰。
由于受自身成像和测量特点影响以及外界环境因素的干扰,TOF 激光雷达的测量数据存在着各种误差, 可分为系统和非系统误差[2]。系统误差主要是由TOF 激光雷达自身硬件系统产生的实测深度距离高于实际距离的情况, 包括谐波相关误差、相位缠绕等[2-3]; 非系统误差一般是使用环境的差异导致的,包括像素饱和、积分时间等[2,4]。
提升TOF 激光雷达测距精度是保证低成本TOF 激光雷达精确还原实际应用场景的前提,因此研究TOF 激光雷达测距误差的问题,消除各种测距误差对其广泛应用的影响是非常有必要的。影响测距误差的因素有很多,本文主要研究积分时间对TOF 激光雷达测距误差的影响。积分时间是指照明调制和传感器解调都有效的时间, 又称曝光时间。对于TOF 激光雷达来说,影响其成像阵列接收环境光的参数只有积分时间[5]。积分时间的长短会影响到TOF 激光雷达接收到的环境光的强度,从而影响测距过程的信噪比[6]。
Kahlmann 等[7]对深度数据建立1 个查找表来校正积分时间对于测距误差的影响。Radmer 等[8]提出了1 种校正方法, 使用1 个各处具有相同反射属性的物体, 测量不同积分时间下距离的误差,通过建立查找表, 对距离进行标定, 并结合线性插值对于查找表中不存在的距离和积分时间进行标定。Lindner 等[9]分析了接收光的强度对深度误差的影响, 通过建立误差查找表(look-up-table,LUT),对光强和距离影响的深度图像提出了校准方法。Steiger 等[10]研究了温度、距离、积分时间、反射率等多种因素对TOF 激光雷达深度误差的影响,提出了设置最佳全局积分时间的方法。
本文采用基于脉冲调制法的TOF 激光雷达,首先采集不同积分时间下的原始数据; 然后对数据进行先行处理;再根据处理后的数据计算距离;最后基于计算结果详细分析不同积分时间对测距误差的影响。最终得出TOF 激光雷达在最佳积分时间下测距平均绝对误差下降为22 mm,误差下降率为97.23%,均方根误差为0.8 mm,测距准确度大大增加。
1 TOF 激光雷达相关原理
1.1 TOF 技术原理
TOF(飞行时间法), 顾名思义就是通过测量光的飞行时间来求取距离,它通过采用CCD/CMOS 成像阵列结合主动红外激光调制技术来获取距离信息, 通过给被测目标连续发送红外激光脉冲, 然后传感器成像阵列接收被反射的红外激光脉冲,通过计算发射光脉冲与接收光脉冲的相位差或时间差,能够进一步获得系统与被测目标之间的距离[11]。根据测量传播时间方式的不同, TOF 技术又可分为直接测量法(direct-TOF, d-TOF) 和间接测量法(indirect-TOF,i-TOF)。本文主要介绍了i-TOF 技术。
TOF 激光雷达利用间接测量法测量距离是通过解调发射光与接收光的相位差实现的。即:
由式(1)、(2)可得:
根据式(1),式(3)也可改写为
式中:d为TOF 激光雷达到被测目标的测量距离;调制频率为f;调制波长为λ;周期为T;发射光与接收光的相位差为∆φ; 光速c= 3×108m/s;n为发射光与反射光之间的周期数。
1.2 脉冲调制法
TOF 激光雷达能够同时获得幅值图(强度图)和深度图,幅值图表示每个像素接收到光子的数量,用以表征光的强度;深度图上的每个像素则编码了到目标物中对应位置的深度信息。根据调制方法的不同, i-TOF 又可分为脉冲调制法和连续波调制法[12]。本文主要介绍脉冲调制法。
脉冲调制法发射光脉冲能量较高, 抗环境干扰能力较强, 信噪比较高。发射的光脉冲通常使用方波脉冲调制,因为它相对容易用数字电路实现。接收端CMOS 成像阵列中的每个像素都是由将入射光转换成电荷的光电二极管、高频转换开关、充电电容组成。该结构可以把电荷导入不同的电容中。
系统在工作时,控制单元打开照明单元,发出1个光脉冲,同一时间,控制单元打开1 个接收端的电子快门,此时接收端接收到的电荷q0被存储到电容中,记为S0。然后控制单元关闭光源,打开第2 个接收端的电子快门,同时关闭第1 个电子快门,即在光源关闭的时间点打开。此时接收到的电荷q1也被存储到电容中,记为S1,如图1 所示[13]。
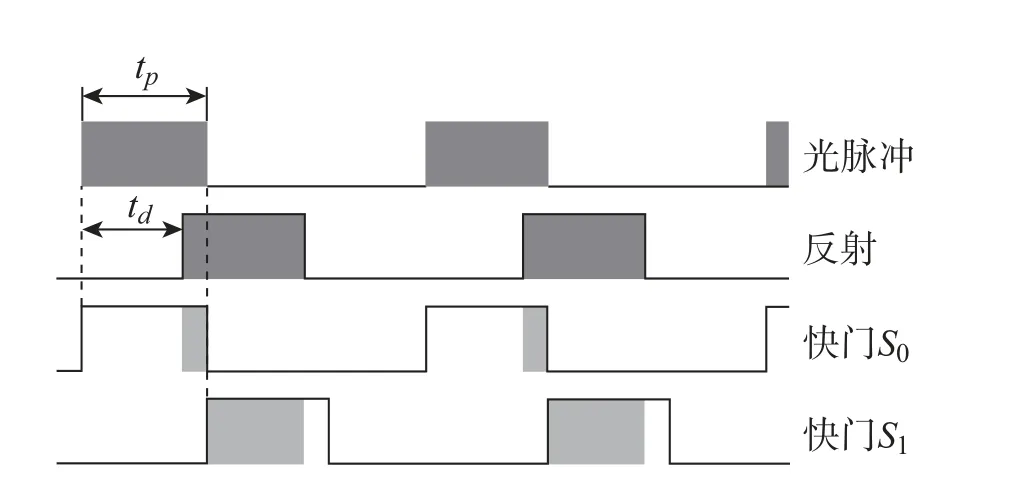
图1 光脉冲发射与接收示意图Fig.1 Schematic diagram of optical pulse transmission and reception
假设tp为光脉冲持续时间,td为光脉冲的飞行时间,c为光速,理想情况下,由脉冲调制法可推导出距离d的计算公式如下:
1.3 TOF 激光雷达测距原理
TOF 激光雷达测距原理如图2 所示,α是激光器半发射角, 其数值为45◦, 视场角(field of view,FOV)是CMOS 传感器水平视场角,其数值为90◦。
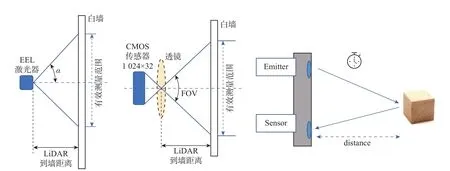
图2 TOF 激光雷达测距原理图Fig.2 TOF LiDAR ranging principle diagram
TOF 激光雷达系统主要由光源发射模块和感光接收模块两部分组成[14]。光源发射模块主要由发光单元、衍射光学元件(diffractive optical elements,DOE)等构成。发光单元为能发出波长940 nm 的边发射激光器(edge-emitting laser, EEL); 扩散板(diffuser)是DOE 衍射光学元件的一种,也属于波束整形器, 主要是提供1 个均匀的面光源。感光接收模块主要由窄带滤光片和光学镜头、CMOS 传感器等构成。镜头的焦距为8 mm。CMOS 传感器为矩形成像阵列,其成像像素为32×1024。
本实验所用TOF 激光雷达可以采用垂直腔面发射激光器(vertical-cavity surface-emitting laser,VCSEL),但是由于EEL 功率密度、脉冲峰值功率更高,整体实验效果更好,故本文采用EEL,平均功率满足人眼安全标准。
CMOS 传感器通过驱动时序实现开窗读出功能, 又称感兴趣区域读出功能, 可以读出CMOS 传感器成像阵列中感兴趣的区域。CMOS 传感器每个像素点都可以接收光脉冲,并且按照Ambient 窗、A窗、B 窗的时序接收光信号,如图3 所示。
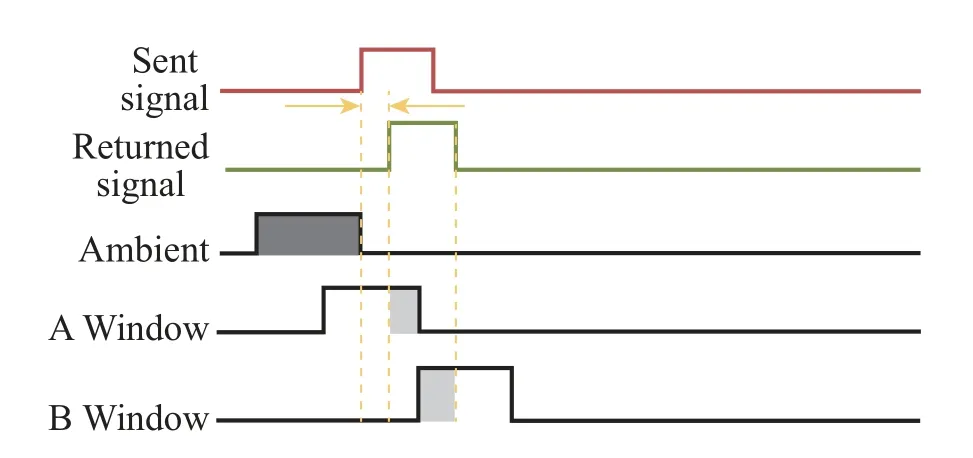
图3 各个像素点光脉冲接收时序图Fig.3 Timing diagram of light pulse reception at each pixel
Ambient 窗是在激光器发射光脉冲之前接收环境光,接收到的环境光强度如图4 所示。
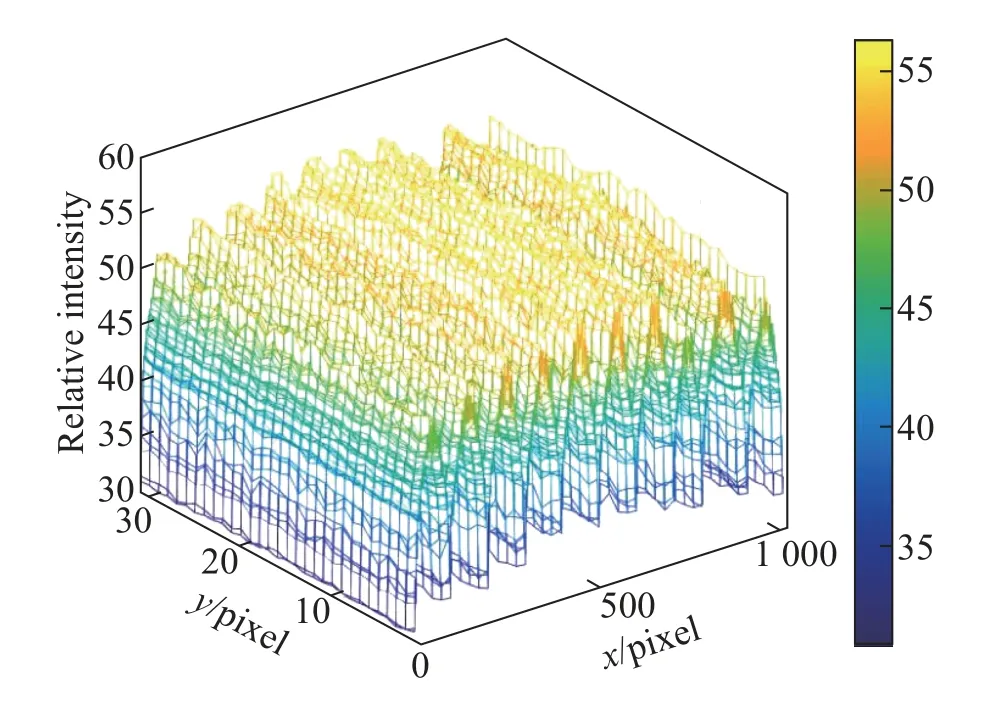
图4 CMOS 传感器接收环境光强度图Fig.4 CMOS sensor receives ambient light intensity map
为了保证能在第一时间接收到反射光脉冲,通过控制驱动时序在脉冲发射之前打开A 窗开始接收电荷。脉冲发射完毕之后,关闭A 窗,打开B 窗接收反射光脉冲。为了保证3 个窗接收到的环境光的一致性,Ambient 窗、A 窗、B 窗3 个窗持续时间一致,且为了保证A 窗、B 窗能够接收到1 个完整的反射光脉冲,窗口的持续时间不短于2 倍的光脉冲持续时间。
TOF 激光雷达测距时,EEL 激光器发射波长为940 nm 的脉冲激光,经过扩散板之后扩散为发射角为90◦的均匀面光源,照射到表面光滑的白墙上。经白墙反射回来的光脉冲经小孔成像,最终被CMOS传感器收集。基于以上原理, TOF 激光雷达每个像素点的距离计算公式为
式中:α为比例系数假设为1;c为光速(m/s);Tw为激光的脉冲宽度25 ns;SA(x,y)、SB(x,y)、SM(x,y)分别为A、B 窗和Ambient 窗接收的光脉冲的强度数值;(x,y)表示像素点在传感器上的位置坐标;Toffset为系统补偿的误差时间,通常设置为5.5 ns。
2 TOF 激光雷达测距实验方案
2.1 实验流程
基于上述原理所设计的实验流程如图5 所示。首先, 通过USB 接口将TOF 激光雷达与上位机互连。然后调整镜头的焦距,在上位机上设置TOF 激光雷达系统增益、积分时间、帧率等相关参数。接着利用上位机软件观察实验情况, 采集实验数据。最后利用matlab 软件对实验数据进行分析处理。
图5 实验流程图Fig.5 Experimental flow chart
2.2 数据处理流程
实验采用的是基于自主设计的TOF 激光雷达,采集的实验数据中存在各种误差,为了更好的分析积分时间对TOF 激光雷达测距误差的影响,针对原始数据先行处理。数据处理流程图如图6 所示。①利用TOF 激光雷达进行待测距离的测量,利用上位机软件采集不同积分时间下的原始数据;②采用均值滤波算法对采集得到的原始数据进行预处理,降低噪声导致的误差;③根据经过预处理后的数据和信号相对强度进一步滤除低幅值的像素区域,选取有效区域的数据;④将选取的有效区域的强度数值代入式(8)中计算测量的距离。

图6 TOF 激光雷达数据处理流程图Fig.6 TOF LiDAR data processing flow chart
2.2.1 均值滤波
均值滤波是一种的线性滤波算法, 用当前像素点某邻域窗口内所有像素值的均值来代替当前像素值。计算公式如下:
式中:G(x,y) 为数字滤波后当前像素点的像素值;S(x,y)为窗口内像素点的像素值,即接收到的反射光脉冲的强度值;n为窗口内像素点总个数;k为窗口内像素点的集合。
使用该方法遍历处理图像内的每一个像素点,可完成整幅图像的均值滤波。本实验采用的是5×5个像素的窗口对采集得到的原始数据进行预处理。以积分时间为600µs 为例,经过预处理之后的数据对比图如图7 所示。
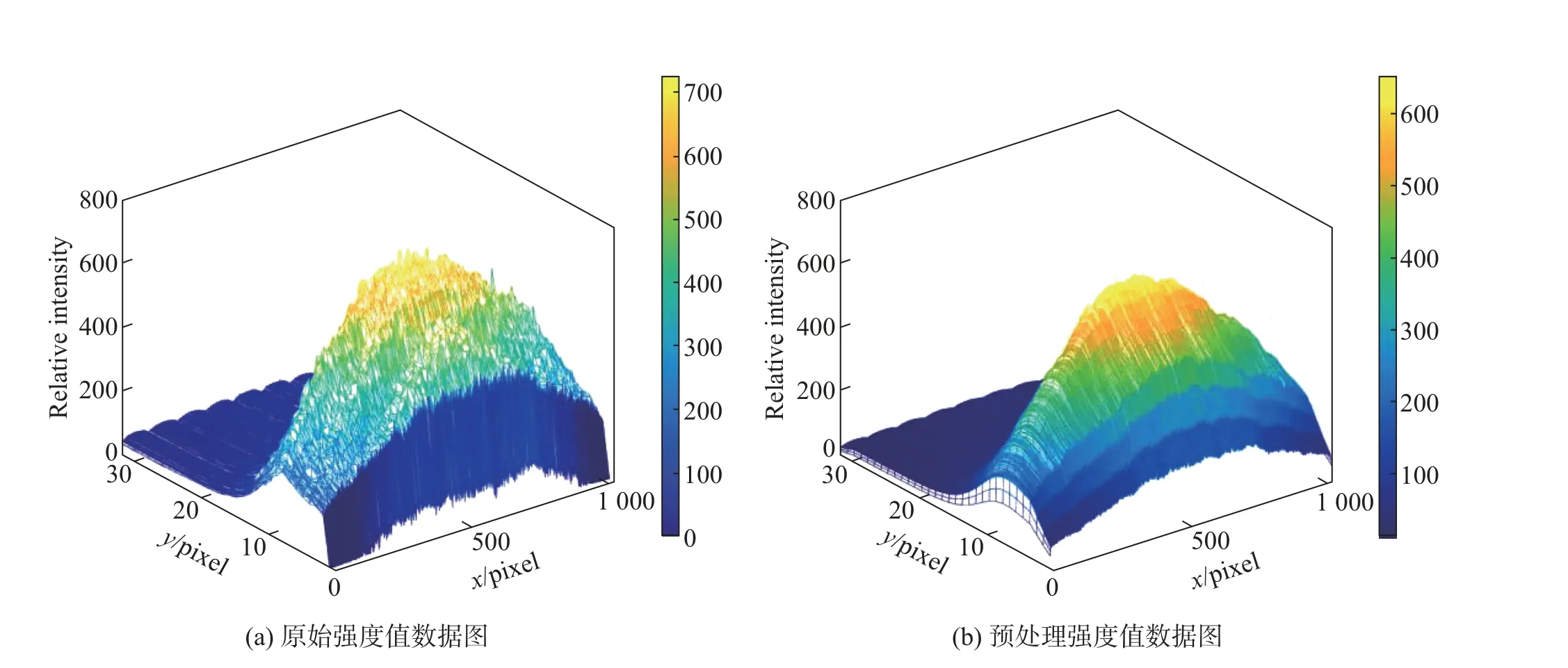
图7 均值滤波预处理前后对比图Fig.7 Comparison of before and after mean filtering pre-processing
2.2.2 选取有效区域
当主动光对场景照明的强度降低时,将导致信噪比降低,从而引起测距误差,这种情况导致的误差和像素幅值的不一致性有关[15]。同时由于受到制造工艺的限制, 对于CMOS 传感器而言, 所有的像素点都是好的情况几乎不可能,会存在一定数量的坏点,导致不能有效成像或相应不一致性大于参数允许范围。坏点接收反射光的光子数量较少, 信号强度较弱, 从而增大测距的误差。这就导致传感器会产生数据无效的区域。因此在进行实验数据的处理时需要滤除数据无效的区域,即滤除相对强度较低的像素区域,选取数据有效的区域,来解决相对强度过小的问题。本文选取20×100 个像素的有效区域,并将有效区域中的强度数值代入式(8), 计算得到测量的距离。
3 积分时间对测距误差影响的分析
在环境光强一定的情况下, 接收到的反射光量与积分时间呈正相关。但CMOS 传感器具有饱和值,其值与器件的物理结构、材料和积分时间等因素相关。饱和值代表了最大可检测的信号强度。光电二极管接收到反射光而产生的电子,需要临时存储在电容里,等待被读取。电容不断累积光电子,随着积分时间的增加,光子数量不断增加,电容逐渐饱和,无法再接收更多的光。CMOS 传感器成像阵列每个像素点存在阈值为1024,即:
积分时间在150∼900µs 之间,每隔50µs 进行调整。TOF 激光雷达到光滑墙面距离为0.6 m。通过对不同积分时间下测量均值、平均绝对误差、均方根误差、误差率的比较, 分析积分时间对误差的影响,如表1 所示。
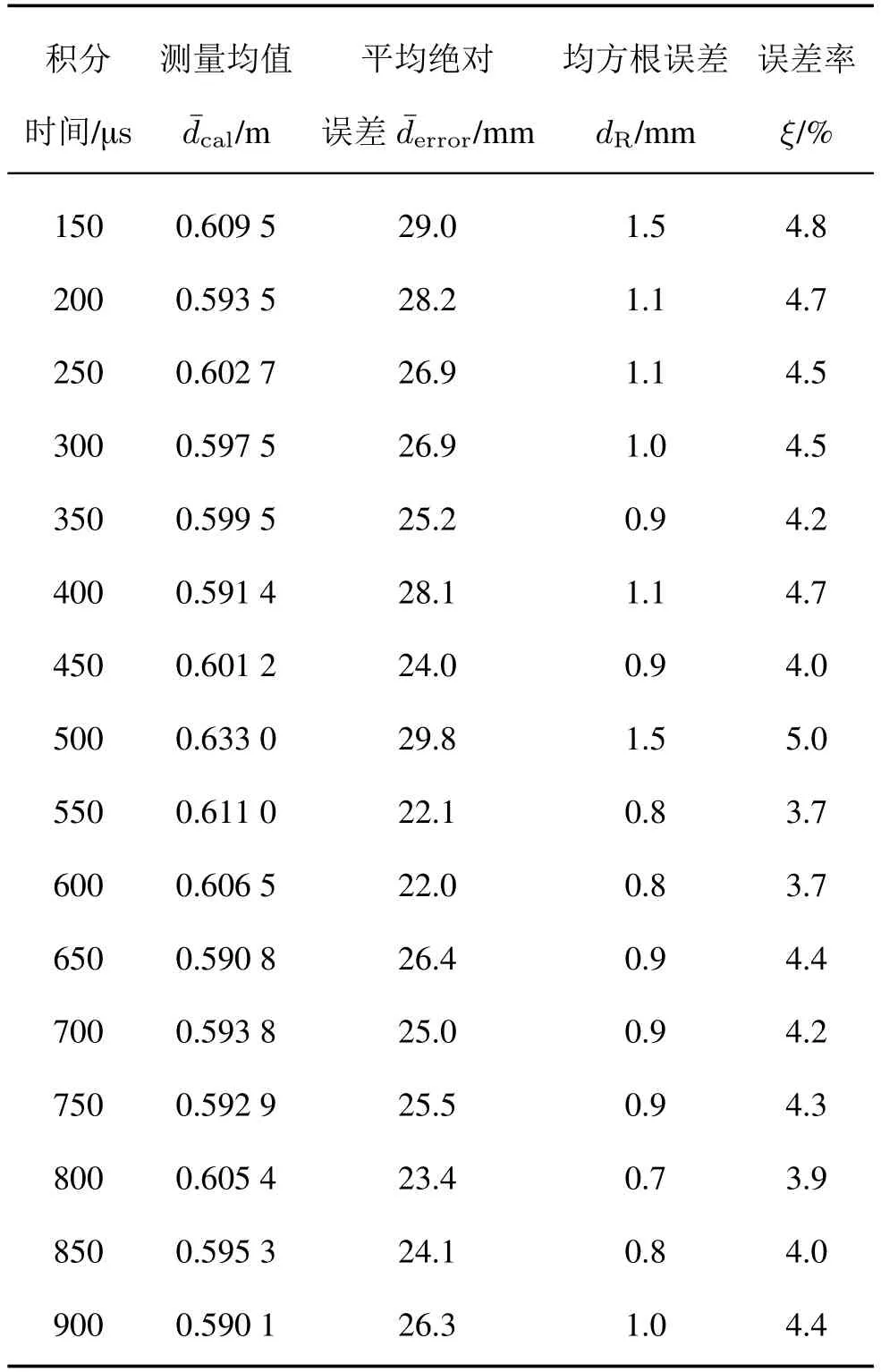
表1 不同积分时间下测量均值、平均绝对误差、均方根误差和误差下降率Tab.1 Measurement mean, mean absolute error, root mean square error and error decline rate at different integration times
TOF 激光雷达的测量均值是选取区域内所有像素点计算得到的距离的平均值,计算公式为:
式中:P为选取区域的行数,取10;L为选取区域的列数, 取200;P·L为选取区域内像素点总个数为2000。
由三角函数关系可得,理想状态下的距离如下式所示:
式中:dideal表示水平方向第N个像素点对应的理想距离,N(1 ≤N≤1024,N ∈Z)表示水平方向第N个像素点;dreal是TOF 激光雷达与白墙之间的真实距离。
CMOS 传感器每个像素点计算得到的距离与理想距离之间的误差值derror计算公式如下:
CMOS 传感器的平均绝对误差是选取区域所有像素点误差绝对值的平均值,计算公式为:
式中:P为选取区域的行数,取10;L为选取区域的列数,取200;P·L为选取区域内像素点总个数,取2000。
均方根误差表示1 组数据的离散程度,能够很好地反映出测量的精密度。均方根误差可以评价数据的变化程度,dR值越小, 说明预测模型描述实验数据具有更好的精确度。计算公式为:
式中:P为选取区域的行数,取10;L为选取区域的列数,取200;P·L为选取区域内像素点总个数,取2000。
误差下降率为
式中:β是原始数据计算得到的平均绝对误差;θ是校正后得到的平均绝对误差; 误差率ξ表示平均绝对误差与理想距离之间的比值,即
通过折线图可以直观地看出不同的积分时间与平均绝对误差、均方根误差、误差率之间的关系。由图8 可见, 积分时间在600 µs 处, TOF 激光雷达测距的平均绝对误差达到最小,且在600µs 附近的积分时间误差均有效可靠。因此积分时间过长或过短,均会导致测距误差的增大;由图9 可见,TOF 激光雷达测距的均方根误差在600µs 处达到最低点,即TOF 激光雷达在此积分时间600µs 下测距最为稳定, 积分时间过长或过短, 都会对测距的稳定性产生降低的影响;由图10 可见,不同积分时间与误差率的关系折线图与平均绝对误差折线图基本一致,这也从侧面证明了图8 所展现的规律:积分时间过长或过短, 均会导致测距误差的增大。故在利用TOF 激光雷达进行距离测量时,需将积分时间设置为600µs 及其附近,以最大程度的减少积分时间带来的误差。
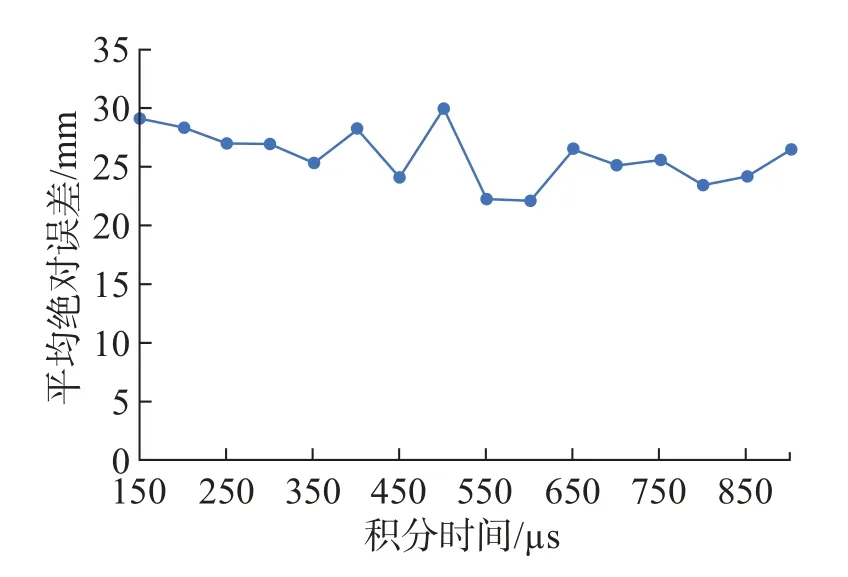
图8 不同的积分时间与平均绝对误差的关系Fig.8 Relationship between different integration times and mean absolute error
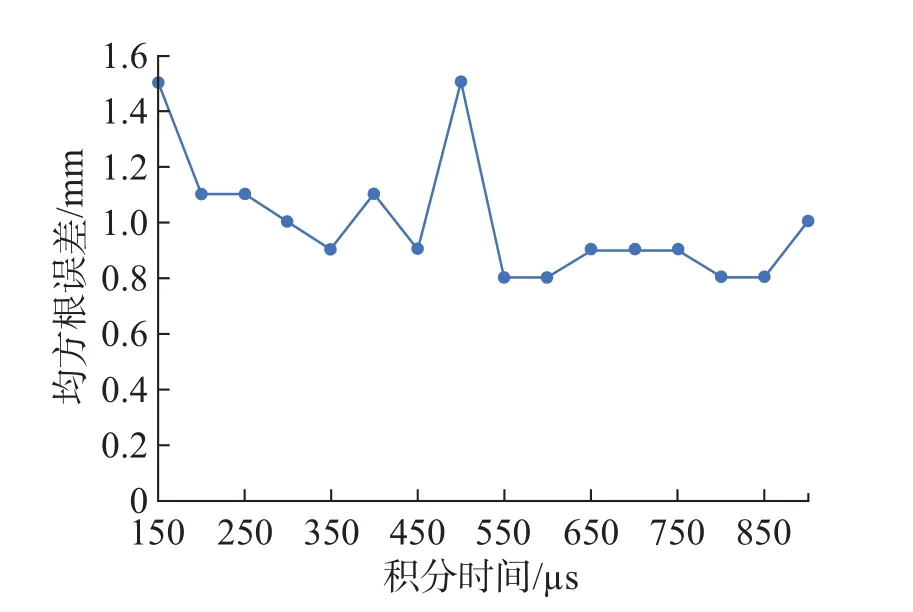
图9 不同的积分时间与均方根误差的关系Fig.9 Relationship between different integration times and root mean square error
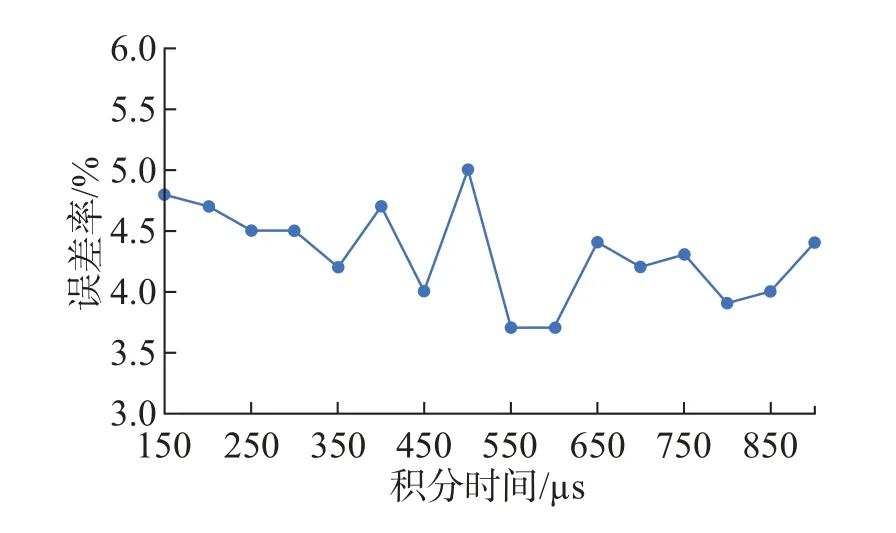
图10 不同的积分时间与误差率的关系Fig.10 Relationship between different integration times and root mean square error
当积分时间设置为600µs 时,实验结果如图11所示,其中图11(a)是TOF 激光雷达在0.6 m 处的测量距离,并与理想距离作对比,图11(b)是测量距离与理想距离的误差值。根据三角函数关系和式(12),选取的有效区域内理想距离与真实距离最大误差为7 mm,可以忽略不计,故采用真实距离0.6 m 代替有效区域内的理想距离,因此计算得到的平均绝对误差为22 mm,均方根误差为0.8 mm。
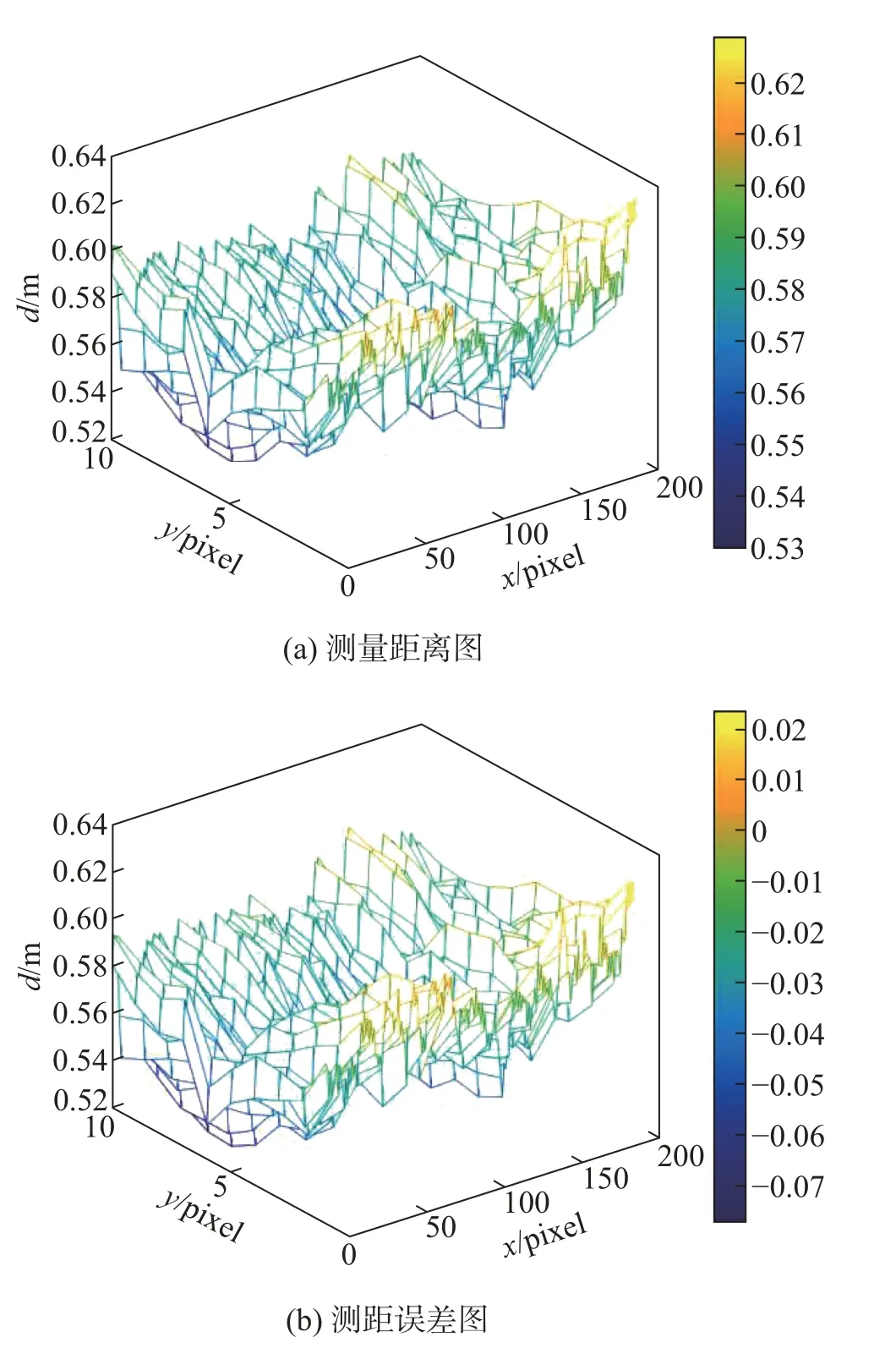
图11 TOF 激光雷达测距图Fig.11 TOF LiDAR distance measurement chart
当积分时间设置为600 时, 根据原始数据计算得到的平均绝对误差为0.7955 m, 均方根误差为0.6457 m,可知误差下降率为97.23%。
4 不同距离实验验证
将上述方法应用到其他不同的距离上,验证方法的普适性,得到如表2 所示的结果。
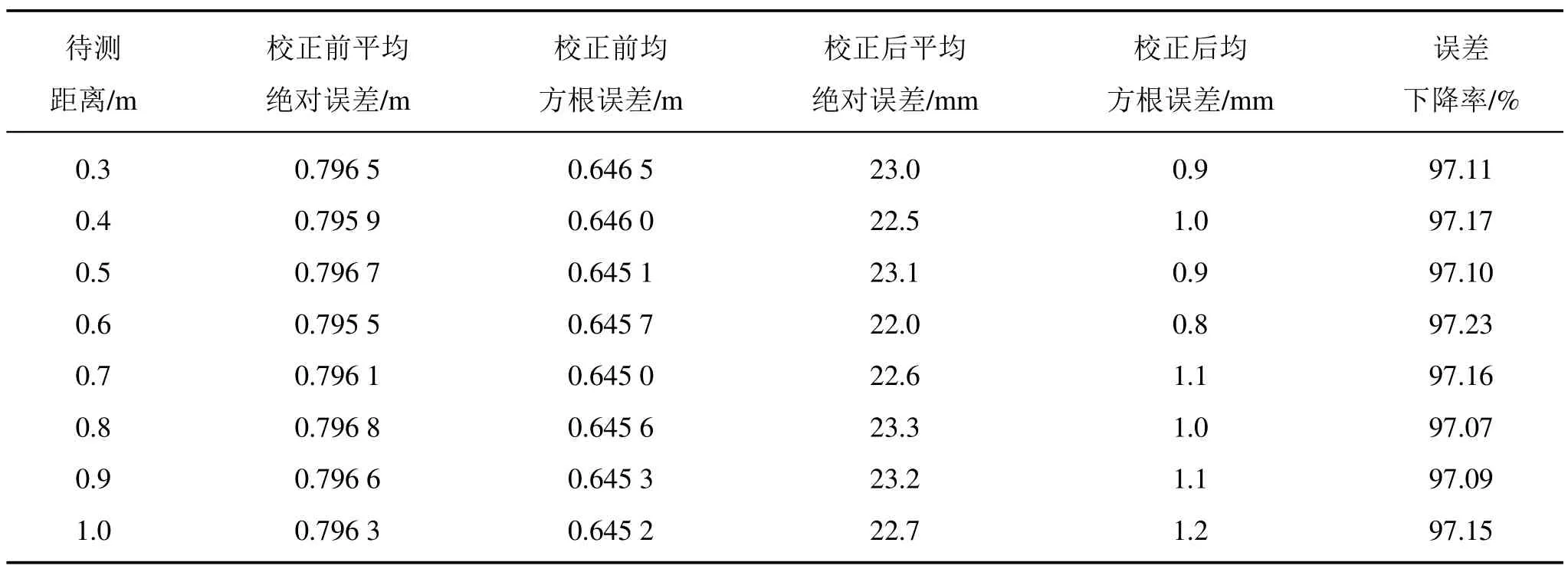
表2 不同距离测距校正前后对比Tab.2 Before and after comparison of different distance ranging correction
由表2 中的数据可见,真实距离在0.3∼1.0 m 之间,TOF 激光雷达测距的误差下降率能达到97%以上, 取得了较为理想的效果。同时可以看出距离的不同对TOF 激光雷达测距误差几乎没有影响。
5 结论
本文分析了飞行时间法的测距原理,介绍了实验室现有的TOF 激光雷达系统的脉冲调制方案以及测距计算方法;通过采集TOF 激光雷达在不同积分时间下的原始数据,并对原始数据进行处理,然后根据处理后的数据计算测量的距离,最后根据计算结果详细着重分析了不同积分时间对测距误差的影响。TOF 激光雷达系统在最佳积分时间下误差下降率达到97%以上,TOF 激光雷达的测距精确度大大增加。为了追求更高的精确度,后续还有很多工作需要进一步研究,如针对不同材质不同反射率的物体进行校正; 针对不同大气环境如烟雾等的影响进行研究。
