基于深度条件适应网络的标签转移算法
2023-09-04刘雪锋李京忠
刘雪锋 李京忠
(许昌市数字化学习工程技术研究中心 河南 许昌 461000) 2(许昌学院城市与环境学院 河南 许昌 461000)
0 引 言
深度神经网络在图像分类、目标检测、图像检索、人体姿势识别等多种计算机视觉任务中取得了巨大成功[1-2]。然而,为每个新任务收集足够的标记数据是一个非常昂贵和耗时的过程,缺乏带注释的训练数据会显著降低深度学习模型的性能[3]。为了解决标签随机性问题,有人提出了一种称为域自适应的方法,其目的是通过转移从相关标记好的源域中学习到的知识来提高无监督目标任务的性能[4]。
域自适应的主要问题是最小化源域和目标域之间的域差异,最广泛使用的解决方案是对训练数据重新采样或学习域公共特征[5]。但是,基于度量的算法在无监督自适应任务的情况下无法适应域条件分布,这种缺点会导致模式不匹配或模式崩溃问题。一些方法试图通过匹配联合分布或条件分布来提高无监督自适应性能。文献[6]用最大平均差进行了边缘和条件适应(MMD)度量和伪目标标签。文献[7]提出了标签结构一致性方法来探索未知目标信息,并实现了条件分布自适应。此外,文献[8]尝试使用加权MMD度量来解决类先验分布偏差问题,其中伪标签被用来减少类权重偏差。最近的一些研究表明,深层神经网络的底层学习域不变表示和结合学习的域自适应算法正在被提出[9-10]。深度适应算法最有前途的方法之一是基于域差异度量,这些算法利用域距离度量显式地减少了域分布的差异,并在许多应用中取得了成功。但是,上述无监督传输方法直接使用源分类器的预测作为伪目标标签,直接预测只基于输出向量的最大值,所以对噪声和域偏移非常敏感,降低了域的自适应性能。
针对上述问题,提出一种基于深度条件适应网络和标签相关传输算法的无监督域自适应方法,通过实验对比验证了本文算法的有效性。
1 深度自适应网络
1.1 相关知识
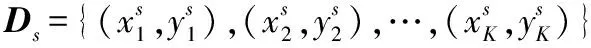
为了更有效地评估分布差异,使用Wasserstein距离来获得更稳定的梯度。给定一个度量空间(M,ρ),两个Borel概率之间的第ρ个Wasserstein距离定义为:
(1)
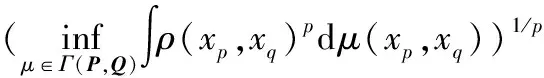
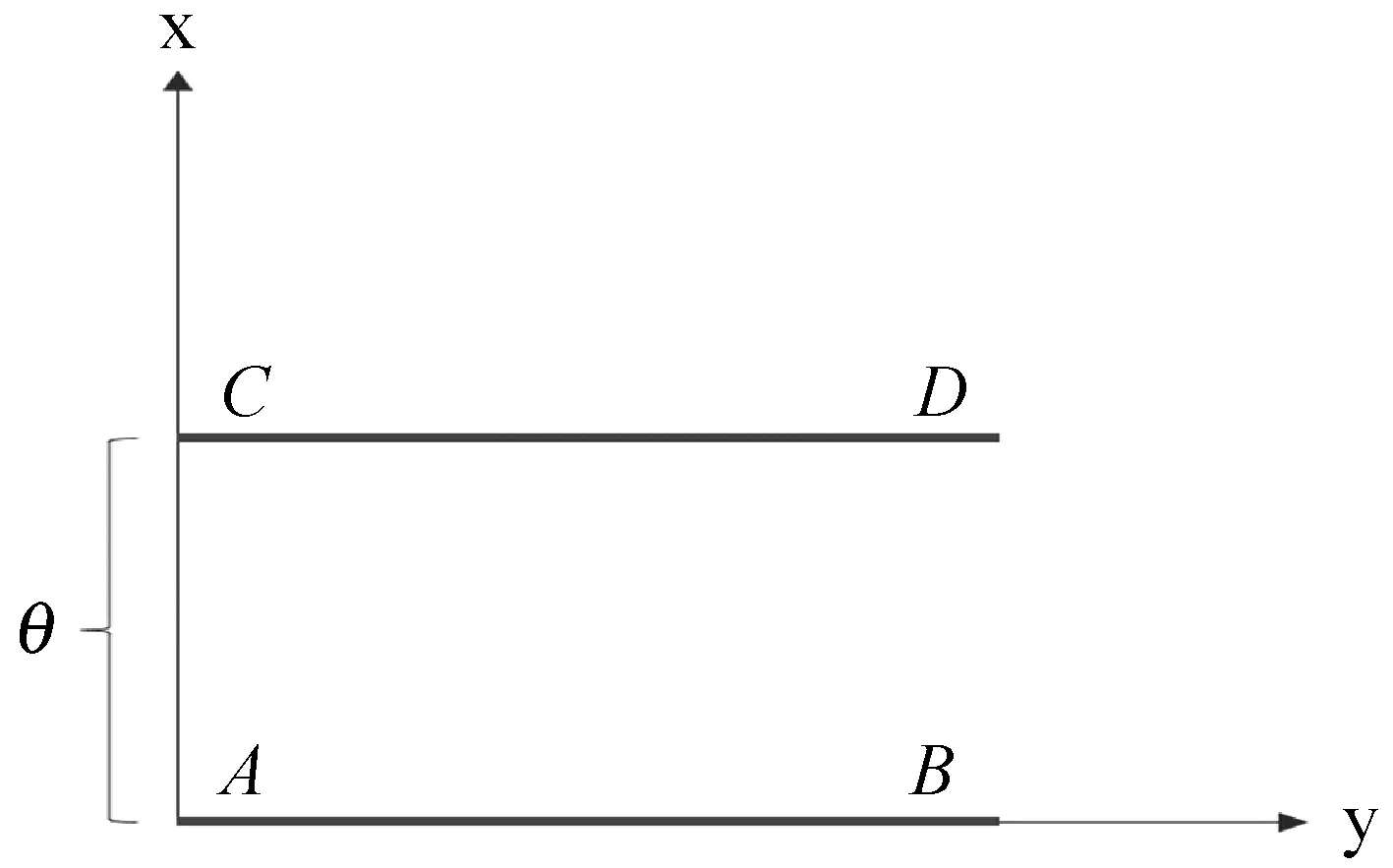
图1 二维空间
Wasserstein距离相比KL散度、JS散度的优越性在于,即便两个分布没有重叠,Wasserstein距离仍然能够反映它们的远近。考虑如下二维空间中的两个分布P和Q,P在线段AB上均匀分布,Q在线段CD上均匀分布,参数θ代表两个分布之间的距离。通过控制参数θ可以控制着两个分布的距离远近。三个散度可以定义为:
(2)
(3)
W(P,Q)=|θ|
(4)
从式(2)-式(4)可知KL散度和JS散度是突变的,要么最大要么最小,Wasserstein距离却是平滑的,如果我们要用梯度下降法优化θ这个参数,前两者根本提供不了梯度,Wasserstein距离却可以。类似的,在高维空间中如果两个分布不重叠或者重叠部分可忽略,则KL和JS既反映不了远近,也提供不了梯度,但是Wasserstein却可以提供有意义的梯度。
1.2 基于DCAN的无监督条件适应
DCAN的框图如图2所示。主要有三个组成部分:特征提取网络fφ、Wasser-stein距离网络fw和分类器网络fc。此外,构造了一个重加权源域,并进行了条件自适应,使目标域和重加权源之间的分布差异最小化。正如前面几节所强调的,本文工作的主要目标是匹配不同域之间的条件分布。在本文中,确定一个特征变换Φ来将跨域数据X传输到特征空间Φ(X),从而存在ps(φ(Xs)|Ys)≈pt(φ(Xt)|Yt)和ps(φ(Ys))≈pt(φ(Yt)),然后通过最小化条件域分布差异来执行条件域自适应。
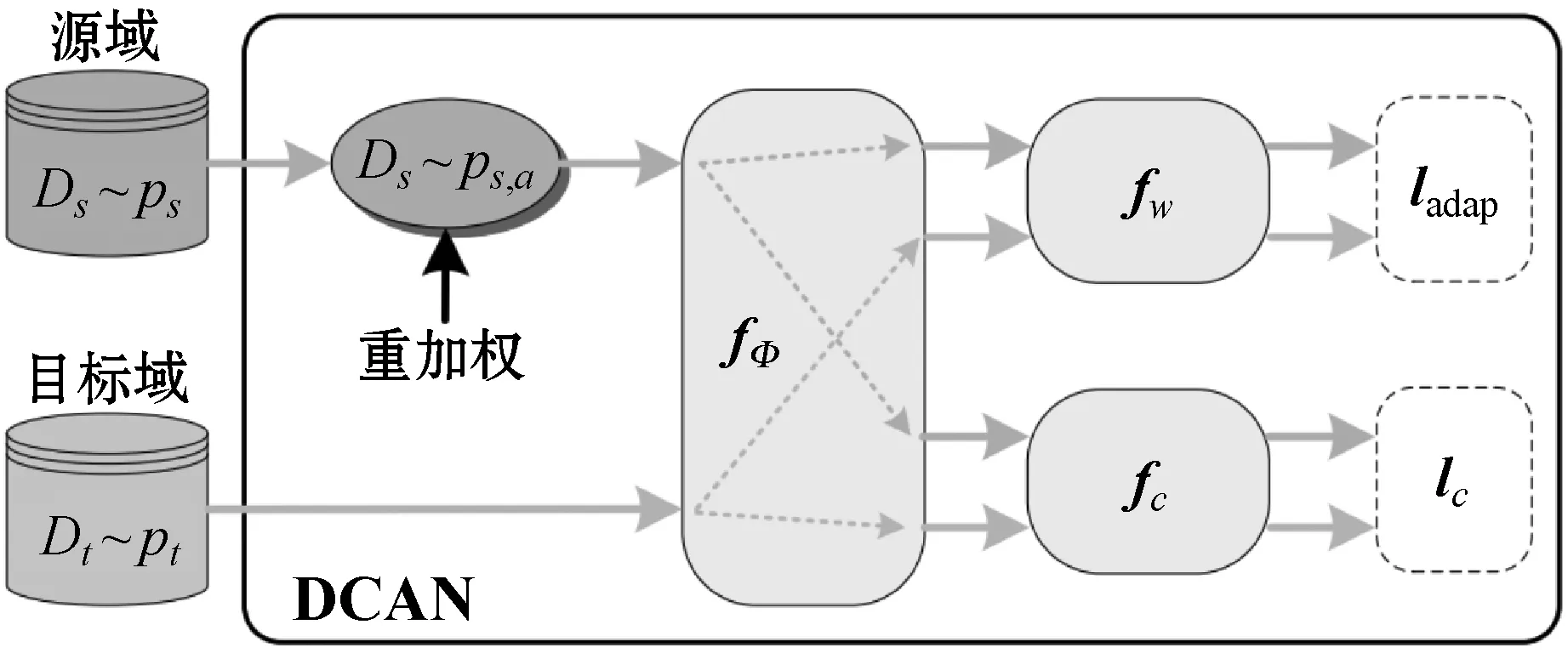
图2 DCAN的框图
构造了两个深度神经网络fφ(X)和fw(h),分别实现了特征传输和Wasserstein距离估计。特征网络fφ(X)有五个卷积层,每层后面由一个汇集层和一个完全连接的层组成。隐藏特征h=Φ(X)=fφ(X):Rm→Rd由fφ(X)生成,其中m和d分别是数据空间和特征空间的维数。Wasserstein网络fw(h)是一个多层全连通神经网络,将Wasserstein距离W1(ps,pt)近似为:
(5)

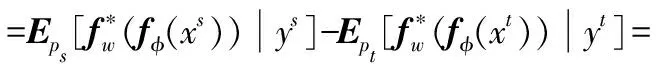
(6)
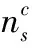
(7)
式中:Wcls表示满足Lipschitz约束的Wasserstein距离;μ为梯度惩罚系数;lgrad表示梯度惩罚因子。最后,构造了一个分类器网络fc(h)来实现图像分类任务。fc的输出是一个典型的Softmax函数,它预测每个输入样本的概率。采用监督学习中广泛使用的交叉熵函数作为分类损失函数:
(8)
结合式(8)和式(9),可以得到DCAN的整个损耗函数:
lDCAN(xs,xt)=lc(xs)+λclassifylc(xt)+
λadapladap(xs,xt)
(9)
式中:u∈{s,t};λclassify和λadap分别是分类和适应平衡系数。DCAN的详细网络架构设置如表1所示。
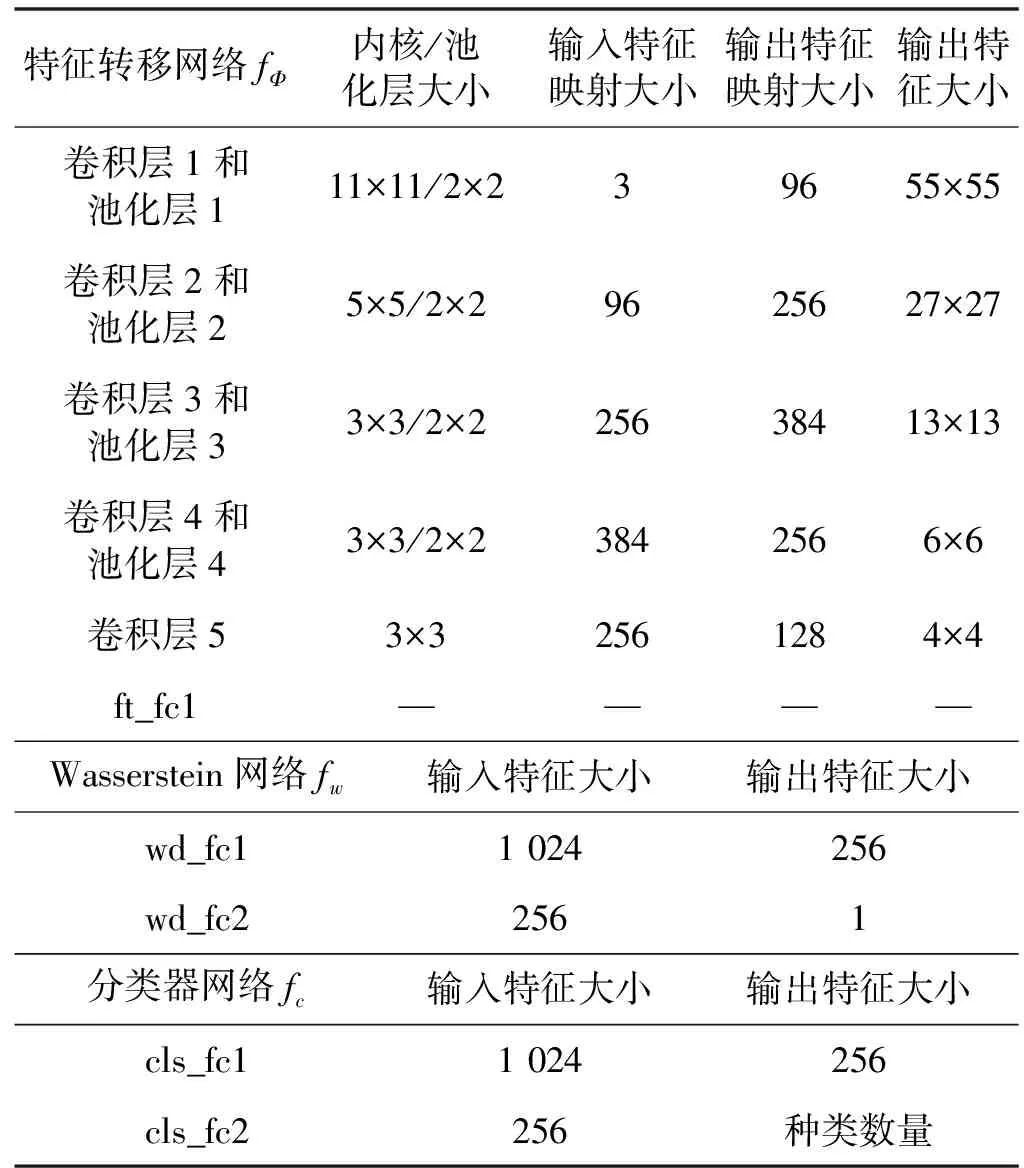
表1 深度条件适应网络的参数
现在考虑类先验偏差问题。首先,构造了一个重加权源分布ps,α(xs),以平衡源域和目标域之间的类偏差。平衡的原理主要根据目标域和学得的源分类器,近似地估计出目标域无标签数据的条件分布,并设定与目标域条件分布相近的源域赋予较大的权值。实例权重法通过调整已知领域中的实例样本的权重提升目标域中辅助域的实例权值,从而更好地适配目标域的数据;该方法着力于如何估算目标领域和辅助领域的概率密度比值。具体的重加权推导可以参考文献[12]。
(10)
式中:αy=c=pt(yt=c)/ps(ys=c)。显然,重加权源分布与目标域具有相同的类先验分布,并保持与源域相同的条件分布。
然后利用Wasserstein距离来计算ps,α和pt之间的差异,得到
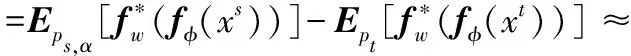
(11)
式中:ns和nt分别是源域和目标域的数目。目标域是未标记的,因此直接计算ladap和lc是DCAN的一大挑战。
1.3 标签相关传输
为了解决无监督的问题,提出标签相关传输算法。如前几节所讨论的,类别之间的关系从源域到目标域是一致的,可以用来预测伪目标标签。
(12)
1.4 DCAN的优化
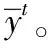
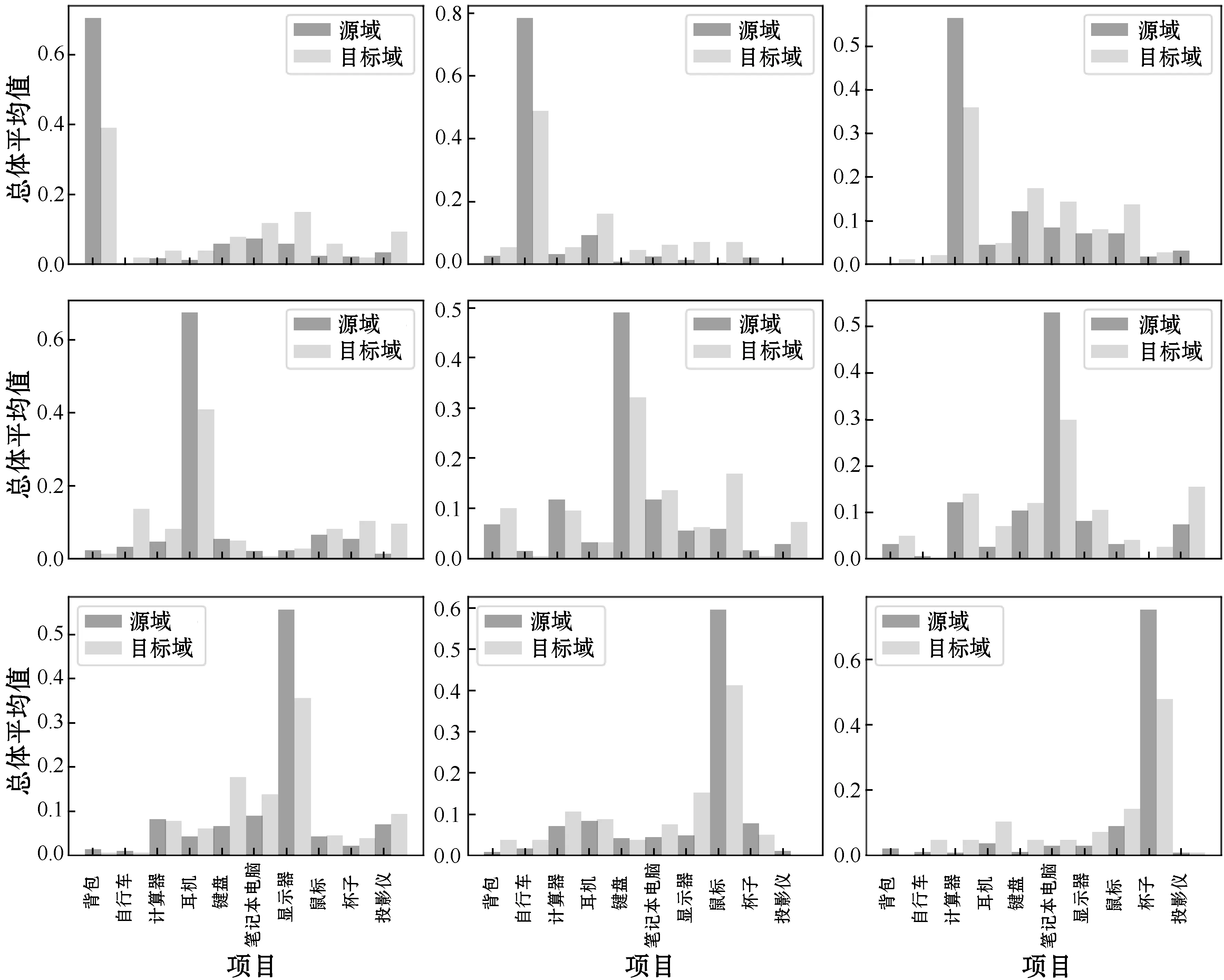
(a) 源样本和目标样本的平均输出分布
当整个优化完成后,分离出最优的fφ-fc网络流,在测试阶段对目标图像进行分类。算法1总结了优化过程。
算法1优化过程算法
输入:源数据{Xs,Ys}和目标数据{Xt}。
输出:优化DCAN模型。
1.通过AlexNet预训练初始化参数fc、fΦ和fw、θw和θc;
2.重复
3.从Xs和Xt采集数据批次Bs和Bt,将Bs和Bt输入fΦ,学习相应的hs和ht;
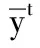
5.更新θw和θΦ:
6.更新θc和θΦ:
7.直到θw、θΦ和θc收敛。
1.5 计算复杂性
与传统的域自适应方法相比,DCAN采用了基于Wasserstein距离的域分布差异评估、类先验偏差求解策略和标签相关转移算法来解决域自适应问题。现在将讨论每种技术的计算复杂性。首先,对于用多层神经网络实现的Wasserstein距离,利用乘法累加运算次数(MACC)来评估时间复杂度。由表1计算可得,Wasserstein网络的MACC为1 024×256+256×1≈2.6×105。这比大多数深度学习域自适应方法广泛采用的特征提取网络小三个数量级。因此,可以忽略Wasserstein距离实现的时间复杂性。其次,对于类先验偏差求解策略,只计算与输入数据个数呈线性关系的重加权参数αy=c。因此,对于大规模数据集,类先验偏差求解策略的时间复杂度是可以接受和实用的。最后,对于标签相关传输算法,计算复杂度为O(n×C2),这对于大规模数据集来说是不切实际的。然而,并不是每次迭代都执行标签相关传递算法。在本文实验中,每十次迭代执行一次该算法,从而大大降低了计算复杂度。总体而言,DCAN的计算复杂度比传统的域自适应方法要大,但这种方法在许多应用中仍然是可行的和实用的。
2 实验与分析
2.1 数据集
在一组实验的基础上使用标准的域自适应基准数据集对DCAN进行了验证。从标签相关性评价、特征可视化和参数敏感性三个方面研究了DCAN的性能。
实验使用四个数据集:Office-Caltech、ImageCLEF-DA、数字识别和虹膜热量/可见人脸数据库。
Office-Caltech是域适应的标准基准。数据集是Office-31和Caltech-256的组合,包括两个数据集之间共享的10个类别。Office-Caltech包含四个域,即A(亚马逊)、W(网络摄像头)、D(DSLR)和C(加州理工)。按照DAN的设置,设置了14个适应任务,A→W,D→W,W→D,A→D,D→A,W→A,A→C,W→C,D→C,C→A,C→W,C→A,C→W,C→D,并采用标准的无监督传输协议。
对于源域,使用所有标记的样本。对于目标域,使用50%的未标记图像进行训练,其余的用于测试。
ImageCrep-DA是为ImageCrep 2014领域适应挑战而开发的。该数据集由五个广泛使用的图像基准(Caltech-256、ImageNet 2012、Pascal VOC 2012、Bing和SUN)之间共享的11个常见类别。使用ImageCLEF的一个子集,包括C(Caltech-256)、I(ImageNet 2012)、P(Pascal VOC 2012)和B(Bing)四个域,然后执行11个转移任务:C→I,C→P,C→B,I→C,I→B,I→B,P→C,P→I,P→B,B→C,B→B,利用所有标记图像进行源域自适应实验。与所有领域相似的Office-Caltech数据集相比,ImageCLEF数据集包含不同分辨率和不同比例的图像,因此可以生成更全面的实验结果。对于Office-Caltech和ImageCLEF-DA数据集,通过将图像裁剪为227×227像素并减去总平均值来对图像进行预处理。
数字识别是一个混合数据集,包含三个子数据集:MNIST、USPS和SVHN。其中,MNIST数据集是由60 000个训练样本和10 000个测试样本组成的手写数字集。每个样品的尺寸为28×28。USPS是一个小规模的数字数据集,共有7 291幅训练图像和2 007幅测试图像,所有图像的大小为16×16。SVHN是一个真实世界的数字数据集,包括73 257个训练数字和26 032个测试数字,图像大小为32×32。建立了M(MNIST)、U(USPS)、S(SVHN)三个域,以及M→U、U→S、S→M、M→S四个传输任务,对数字数据集进行数据预处理:将所有图像整形到16×16,并将像素值重新调整到[0,1]范围内。由于数字识别数据集中的图像尺寸很小,特征提取网络的结构也相对简单。构建了一个两层全连接网络,将图像投影到1 024维的特征向量上。
虹膜热量/可见光面部数据库包含了从30个人采集的4 228对热图像和可见光图像。每个个体的图像都是在不同的光照、面部表情和姿势下获得的。根据图像形态将数据分为可见域(V)和热域(T),然后根据获取条件将每个域划分为三个子域。总的来说,有六个不同的领域,即可见光(VI)、可见表情(VE)、可见姿势(VP)、热照明(TI)、热表情(TE)和热姿势(TP)。然后设置了12个转移任务:VI→VE,VE→VP,VP→VI,TI→TE,TE→TP,TP→TI,VI→TE,TE→VP,VP→TI,TI→VE,VE→TP,TP→VI,前6个任务设置在相同的模式和不同的获得条件下,后6个任务包含不同的模式和获得条件。将人脸识别任务视为一个多类分类问题,以一个秩为1的识别率作为分类得分。
为了评估性能,将DCAN与一些广泛使用的域自适应算法进行比较,包括传输分量分析(TCA)[13]、联合分布自适应(JDA)[14],以及几种最先进的深度传输方法:深度自适应网络(DAN)[15]、标签和结构一致性(LSC)[8]和加权最大平均值差异(WMMD)[9]。为了确保比较的有效性,将DeCAF特性[10]应用于两种非深度学习算法TCA和JDA。选择系数λclassify和λadap分别为0.7和0.4。此外,学习速率初始化为0.003,当损失稳定时乘以0.5。动量参数最初为0.5,在两次迭代循环后增加到0.95,以帮助逃离鞍点。
2.2 实验结果
实验结果见表2-表4。总的来说,很明显,所提出的DCAN在大多数自适应任务上都取得了更好的性能。从结果中得出了几个主要结论。
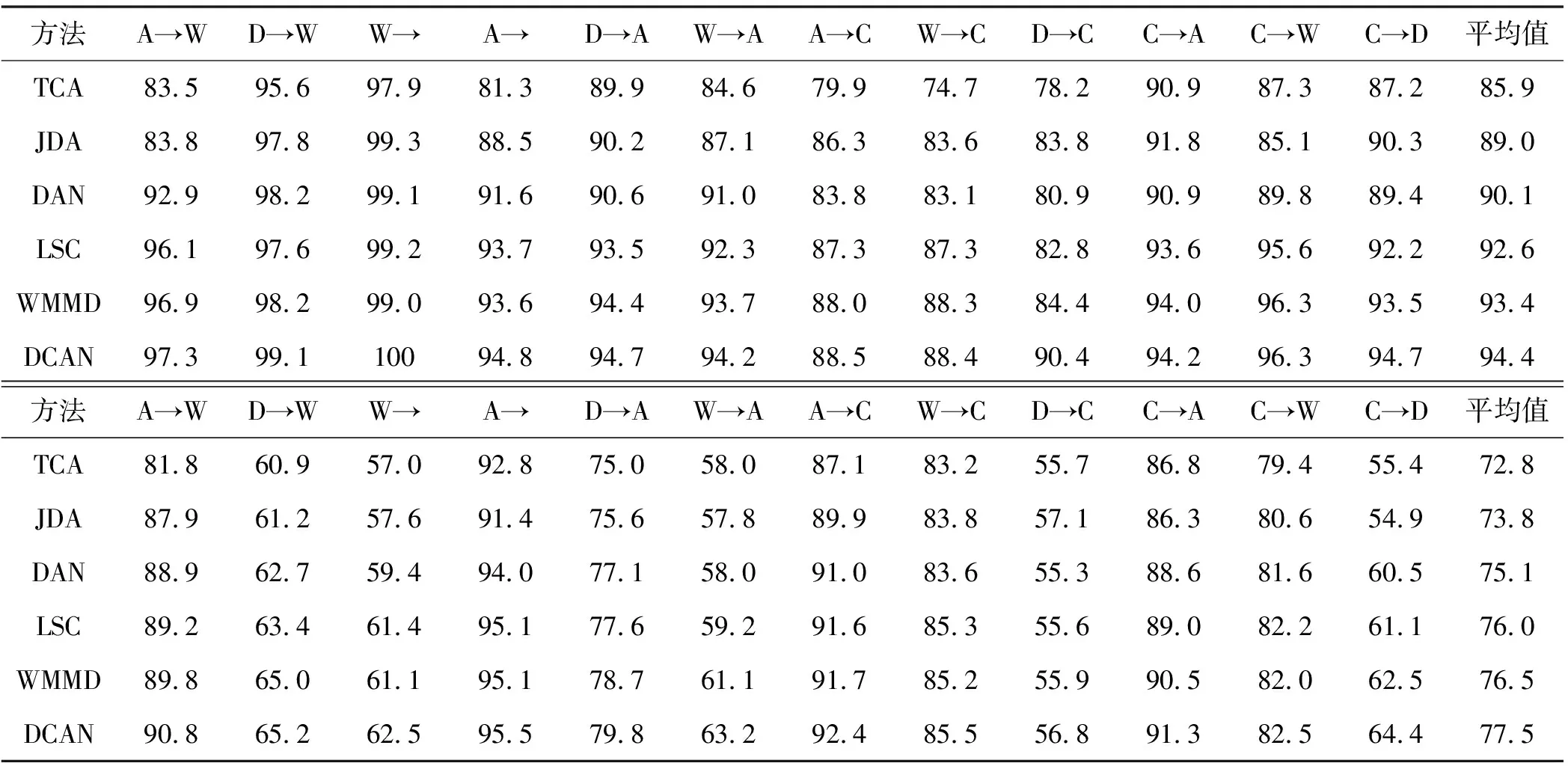
表2 Office Caltech和ImageCrip数据集的标准适配协议的准确率(%)
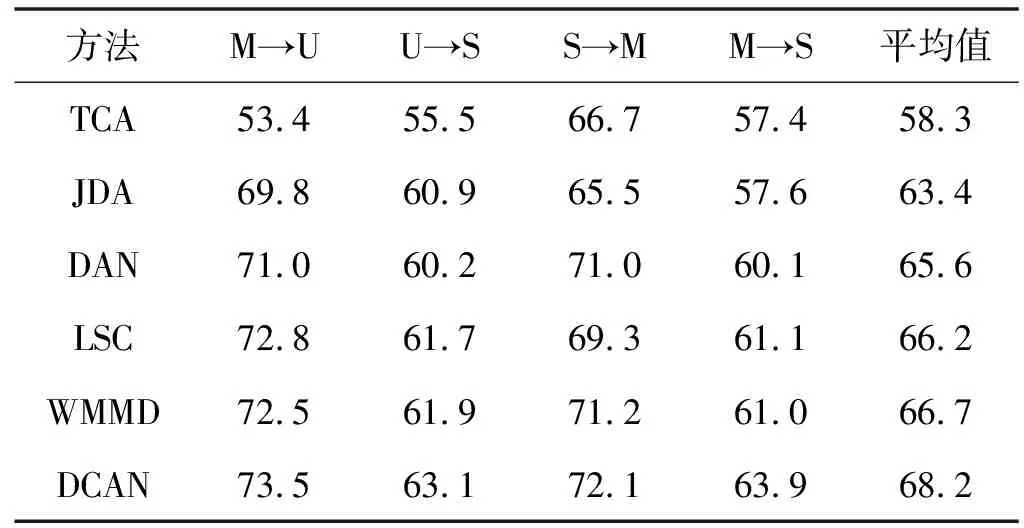
表3 使用标准自适应协议的数字识别数据集的准确率(%)
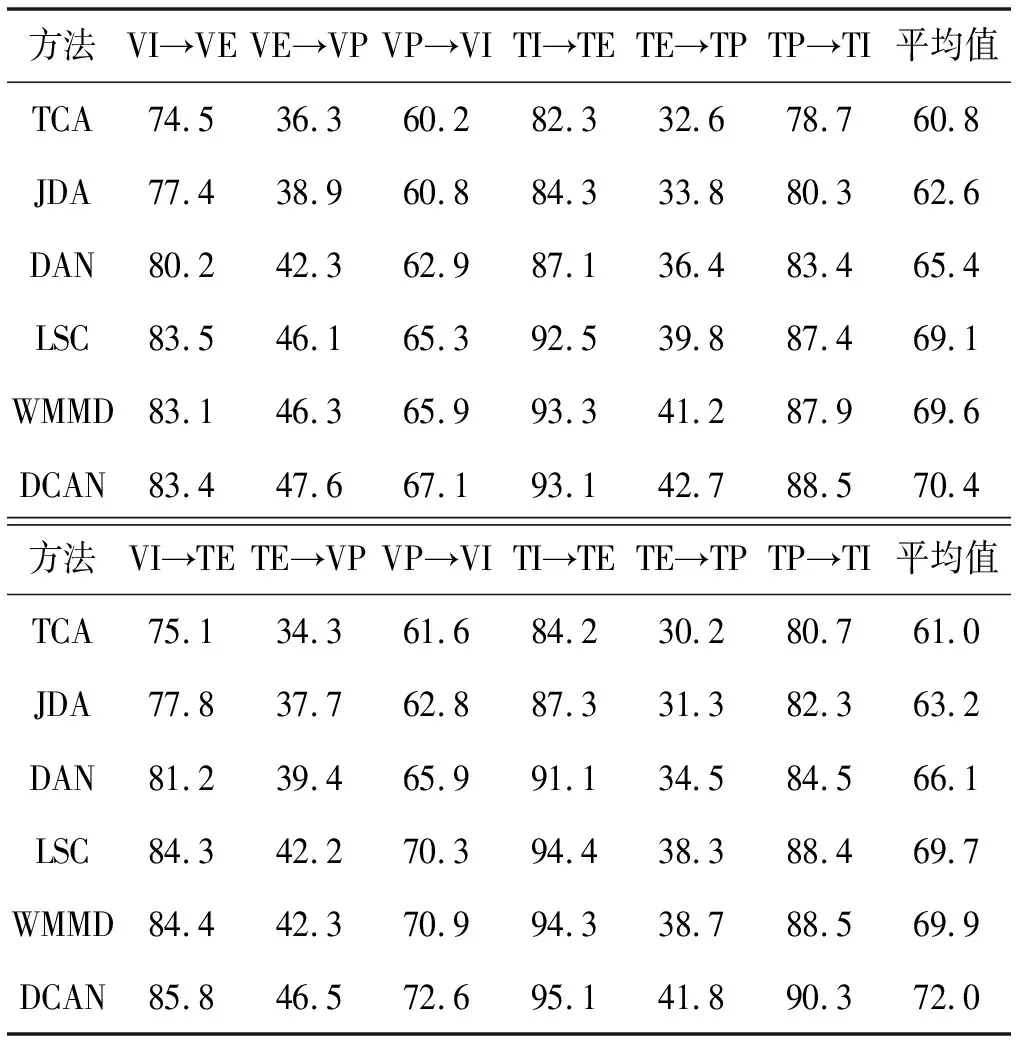
表4 虹膜热量/可见光面部数据库的准确率(%)
1) 与非深度学习方法(如TCA)相比,DCAN的性能明显优越。由于非深度学习方法简单地使用现成的深层特征,无法有效地减少域分布差异。DCAN利用所提出的自适应算法对深部网络进行优化,使DCAN学习到的特征具有更明显的域不变性。这种深度自适应策略有助于提高性能。
2) 与其他深度自适应方法相比,DCAN具有更好的传输能力。这些优势可以归结为两个方面。由于DCAN采用了标签相关传递算法来预测目标域的伪标签,因此可以更有效地解决域失配问题,实现条件自适应。此外,DCAN还解决了类先验偏差问题,进一步提高了跨域分类性能。因此,对于Office Caltech任务,DCAN优于WMMD 1百分点和LSC 1.8百分点,在ImageCrip-DA任务中分别优于WMMD和LSC 1百分点和1.5百分点。特别是对于D→C等困难任务,DCAN比WMMD提高了6百分点,充分证明了DCAN的有效性。
3) 在多模态实验中,DCAN在所有任务上都优于其他方法。这表明了DCAN在解决跨模态问题中的有效性。此外,将前6个任务与后6个任务进行了相应的比较,发现一些跨情态任务的表现优于相同情态的任务,如VI→TE任务。这是因为不同形式的图像可以提供补充信息。DCAN在跨模态任务上获得了1.6百分点的提升,这是所有比较方法中最高的。结果表明,所提出的DCAN能够从不同的模式中学习可靠信息,并能很好地解决跨模式问题。
2.3 分析和讨论
2.3.1标签相关传递研究
在这一部分中,将进一步研究所提出的DCAN,以探索和证明该方法的有效性。本文进行了一系列实验来验证所提出的标签相关传输算法。首先,研究了输出分布的源样本和目标样本之间的关系。在实验中,利用高温训练了一个Softmax分类器。分类器的输出可以看作每个样本的输出概率分布。给出了输出的总体平均值,并计算了这些分布的KL距离,如图3所示。确定了同一类别的目标样本和具有相似分布的样本,这个观察结果证实了提出的标签相关传递算法的有效性。
然后通过实验研究了标签相关传递算法如何提高分类性能。目前大多数的无监督传输方法直接使用源分类器的预测作为伪目标标签。直接预测只基于输出向量的最大值,所以对噪声和域偏移非常敏感。相反,标签相关传输算法考虑了输出的整体分布,因此,它对噪声和域偏移更具鲁棒性。做了一个比较实验来证明这个直觉假设。DCAN的一个变体版本可以通过用直接目标标签预测代替标签相关传输过程来实现。根据从加州理工学院办公室数据集中随机选择的四项转移任务,比较自适应表现,结果如表5所示。可以看出原始DCAN的性能优于改善DCAN,证明了提出的标签相关转移的有效性。
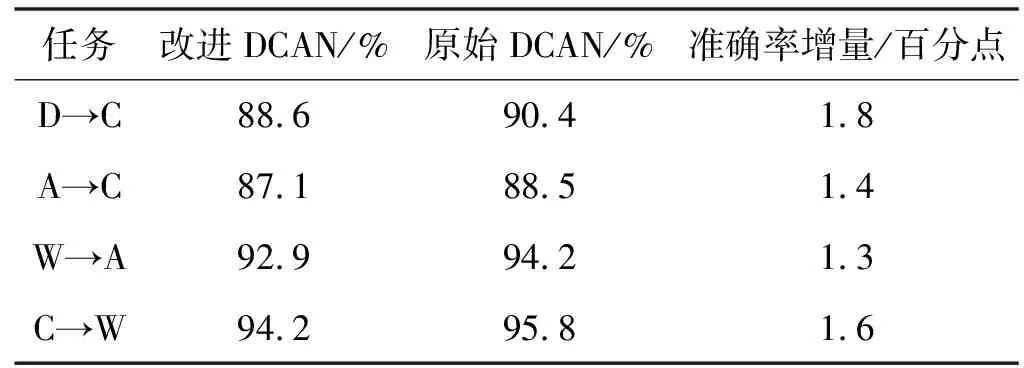
表5 改进后的与原始DCAN的比较结果
2.3.2评价Wasserstein距离的有效性
在本节中,将评估Wasserstein距离在域适应任务中的有效性。当学习不同域之间的差异时,Wasserstein距离比传统距离提供更可靠的梯度。因此,可以更有效地执行域自适应。通过两个实验来证明Wasserstein距离的优越性。首先,评估了一个包含两个具有不同均值和相同方差的高斯分布的合成数据集上的分布差异度量性能。然后使用Wasserstein和MMD方法估计两个高斯分布之间的距离。结果如图4所示。很明显,Wasserstein距离与实际分布距离呈线性关系。然而,当分布相互分离时,MMD距离趋于饱和。这一结果证明了Wasserstein距离用于测量差异较大的区域分布的有效性。
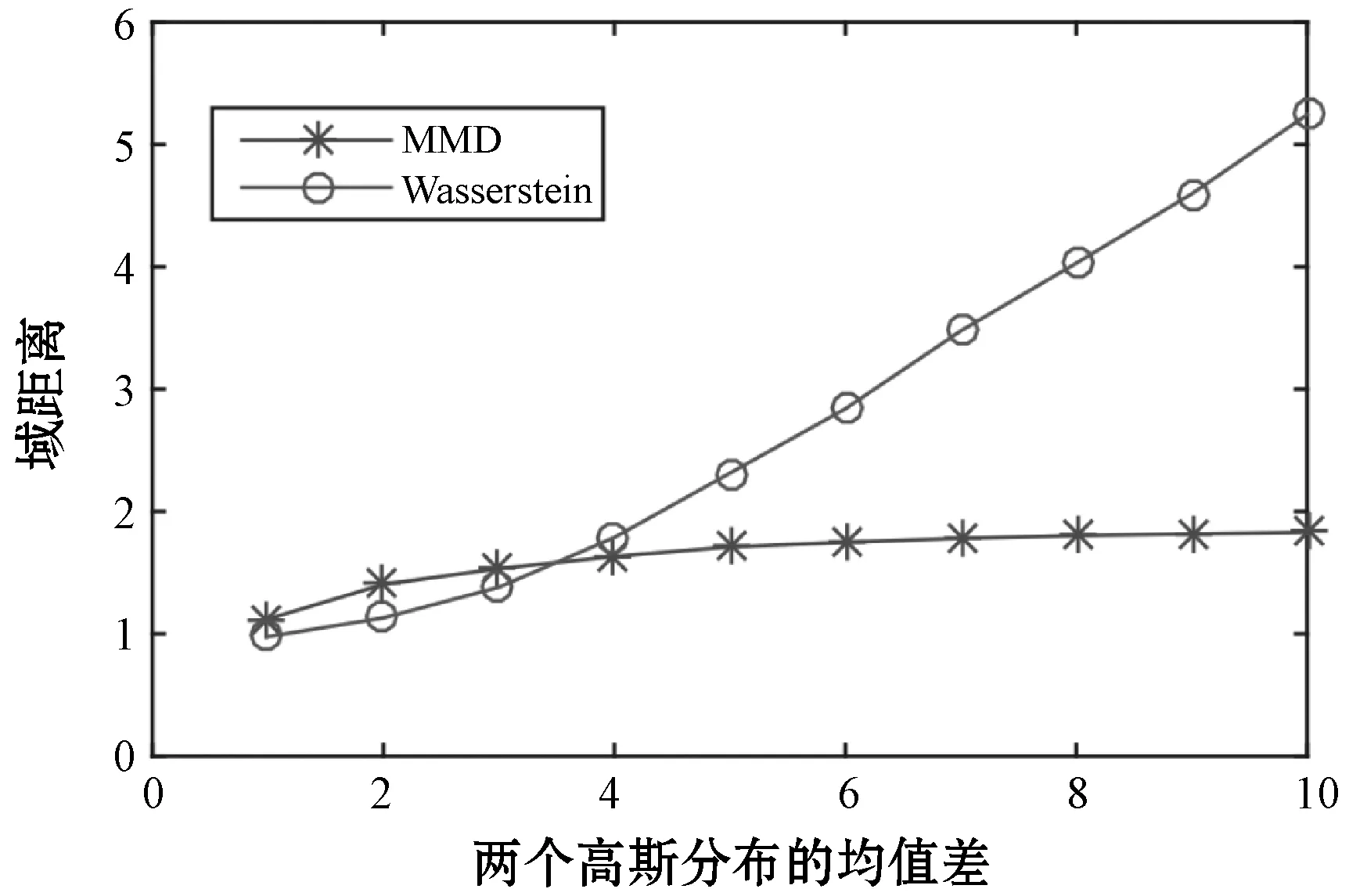
图4 MMD和Wasserstein距离的比较
然后,对Wasserstein距离法在现实世界的迁移任务中的应用进行了评价。用MMD距离代替Wasserstein距离构造了一个变异DCAN,并比较了两种DCAN在四种转移任务上的适应性能,结果见表6。结果表明,基于Wasserstein的DCAN模型优于基于MMD的DCAN模型,特别是对于D→C和C→W等不平衡和困难的转移任务,这一结果表明了用Wasserstein距离来度量域差异的优越性。
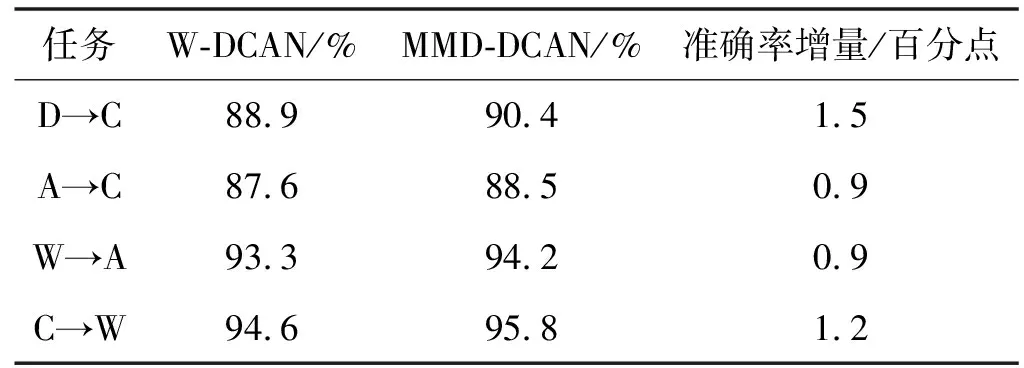
表6 Wasserstein的DCAN和基于MMD的DCAN的比较结果
2.3.3特征可视化
使用t-SNE可视化方法来分析DCAN和DAN学习的特征映射的适应能力。在D→C任务上执行可视化,并在图5中的嵌入特征中示出。可以观察到DCAN的特征比DAN的特征更具鉴别性。特别是圆圈中,DCAN保留了类的距离,避免了DAN中出现的模式崩溃。其根本原因是DCAN执行无监督的条件适应策略。

(a) 任务D→C的DCAN的t-SNE嵌入特征

(b) 任务D→C的DAN的t-SNE嵌入特征图5 DCAN和DAN的特征可视化
2.3.4参数灵敏度
通过改变λclassify∈{0.2,0.3,0.4,0.5,0.6,0.7,0.8,1.0,1.2}和λadap∈{0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1}来研究平衡系数λclassify和λadap的影响。从三个实验中选择六个迁移任务来评估参数敏感性,结果如图6所示。
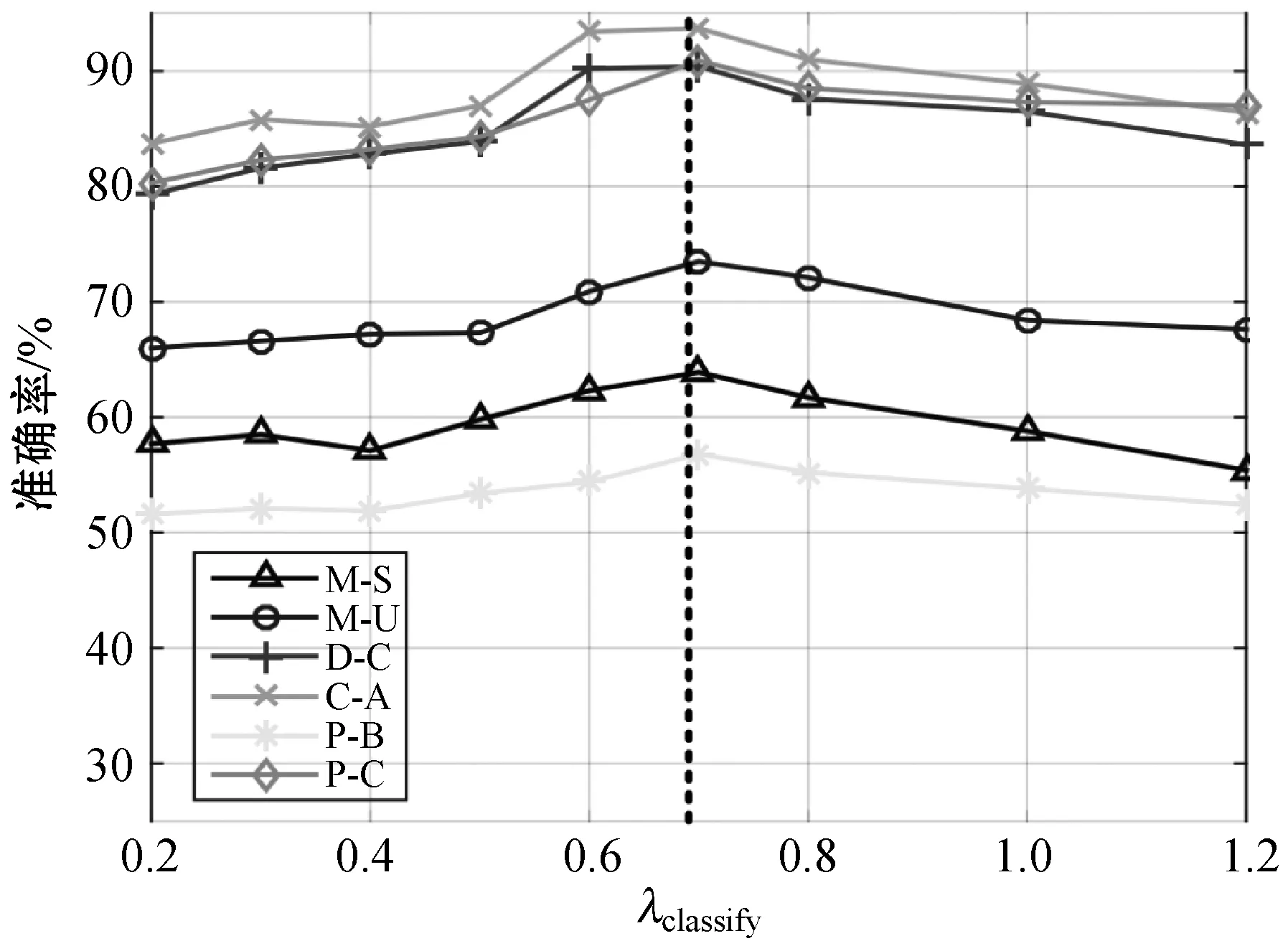
(a) 不同λclassify的分类精度
图6(a)显示了不同参数λclassify下的六个转移任务的分类精度。性能逐渐提高,在0.7左右达到最佳,然后随着λ分类的增加略有下降。这表明,当目标分类损失的比例限制在一定范围内时,目标分类损失有助于提高系统的整体性能。
图6(b)显示了不同λadap的精度。通常情况下,最佳折中参数λadap约为0.4,在极值点(过大或过小)下性能会显著下降。这种钟形曲线表明,分类和适应之间的适当平衡是重要和必要的。
2.3.5收敛性
在实验的基础上分析了所提出的DCAN算法的收敛性。选取了四个跨域任务,报告了域距离和精度随训练迭代的变化,结果如图7所示。可以看出,精度在大约50次迭代时变得稳定,并在200~250次迭代中收敛。具体地说,确定域距离与精度呈负相关。这表明减小域差异可以提高跨域识别性能。这一结果再次证明了所提出的条件域自适应策略的重要性。
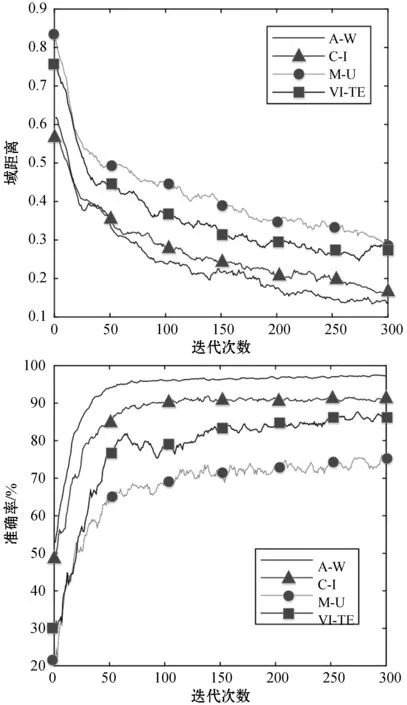
图7 四个跨域任务的收敛性评估
3 结 语
针对目前无监督域自适应方法对噪声和域偏移非常敏感,提出一种基于深度条件适应网络的标签转移算法。通过数据集实例结果分析可得如下结论:
1) 域距离与精度呈负相关,减小域差异可以提高跨域识别性能。Wasserstein距离可以有效度量区域分布差异,有效解决了当邻域差异较大时梯度消失问题,从而获得更好的域适应性能。
2) Wasserstein距离可以有效度量区域分布差异,有效解决了当邻域差异较大时梯度消失问题,从而获得更好的域适应性能。
3) 提出的基于深度条件适应网络和标签相关传输算法的无监督域自适应方法考虑了输出的整体分布,因此,它对噪声和域偏移更具鲁棒性,并且提升了算法的准确性和实用性。
