考虑可控负荷接入的电力系统低频振荡模态辨识方法
2023-09-02王亮
王 亮
(国网宁夏超高压公司,宁夏 银川 750004)
0 引 言
低频率振荡信号是电力系统的发电设备与各个区域间网络在发电运行过程中,受到多种因素相互作用的影响而产生的一种可用于反映电力系统安全性、稳定性以及输电供电可靠性的关键信号[1,2]。随着电力互联网覆盖范围的扩大,电网的规模越来越大,复杂程度越来越高,多种样式的发电机和大功率电力设备被接入电力系统。该运行条件下,电力系统的阻尼性无法得到有效保障,低频振荡越来越频繁。目前,低频振荡现象已经成为我国各地电力局与有关部门关注的重点,若不加以控制或处理,则十分容易造成地区大规模停电事件[3]。为了实现对低频振荡的精准识别,精准排查并及时处理电力系统运行中存在的故障,在考虑可控负荷接入的条件下,以某电力系统为例,设计一种针对低频振荡的模态辨识方法,从而为提升电力系统的可用性提供全面的技术保障。
1 电力系统自由振荡响应信号提取
考虑到系统运行信号在传输过程中会受到多种因素的影响,无法直接获取其自由模态信息[4,5]。为了满足该需求,引进资源调配技术(Resource Director Technology,RDT),以线性系统作为支撑,根据线性系统的运行需求和负荷接入方式,将线性系统接入电力系统。在随机、平稳的激励下,电力系统将反馈响应信号。
当电力系统的发电机转子处于稳定运行状态时,反馈的自由振荡信号为
式中:F(t)表示t时刻下电力系统发电机转子处于稳定运行状态时反馈的自由振荡信号;K表示电力系统惯性系数;∆δ(t)、∆(t)、∆(t)表示系统发电机在运行中的不同角功率;D表示电力系统阻尼频率;M表示定量系统在运行中的同步功率系数。
假设系统运行到ti时刻时触发自由振荡响应条件,则可以在ti时刻后截取电力系统运行的信号片段。此时对应的信号片段为
式中:τ表示截取信号片段的长度。
假设电力系统在运行中满足自由振荡条件的信号区段数量为N,则提取N段电力系统自由振荡响应信号为
式中:x(t)表示电力系统自由振荡响应信号。基于式(1)~式(3),完成考虑可控负荷接入的电力系统自由振荡响应信号提取。
2 电力系统振荡模态信号分解
完成对电力系统自由振荡响应信号的提取后,引进经验模态分解(Empirical Mode Decomposition,EMD)算法,对提取信号中的振荡信号进行模态分解。分解过程中,需要在提取的电力系统自由振荡响应信号中进行初步筛选,去除冗余信号与重叠信号后,将提取的信号表示为原始信号,即x(t)为分解过程中的原始信号。在x(t)中添加若干段长度随机且符合正态分布的白噪声信号,生成一个全新的电力系统信号段,即
式中:xj(t)表示t时刻下生成的全新电力系统信号段;nj(t)表示长度随机且符合正态分布的白噪声信号。在此基础上,对xj(t)进行分解,分解后可以得到若干个本征模函数(Intrinsic Mode Function,IMF)信号分量与余项。将信号分量标记为cij(t),将余项标记为rin(t),则分解后的xj(t)信号可以表示为
式中:n表示分解后的项数。
重复上述步骤若干次,对分解后得到的IMF 信号分量求取平均值,得到信号分量组为
输出分量信号,将其作为振荡模态信号,按照上述方式完成电力系统振荡模态信号的分解。
3 低频振荡频率与振型识别
完成对信号的分解后,将分量信号作为参照,辅助电源管理单元(Power Management Unit,PMU)采集系统发电机运行功率、角信号等实测数据。当系统处于异常运行状态或低频故障运行状态时,系统的测量数据将携带非线性信号与噪声信号。提取此部分信号,将其与分量信号进行比对。根据系统的常态化运行方式,建立系统的状态矩阵,根据系统异常状态的特征值对其状态矩阵进行分解,计算系统在运行中的特征根。在已知电力系统振荡模态特征根的条件下,计算系统的低频振荡频率,实现对系统在运行中低频振荡振型的识别。
4 对比实验
为了检验模态辨识方法在实际应用中的辨识效果,以某地区大型电力服务中心为例,采用对比实验的方式展开测试。
测试前,为了更加直观地掌握系统的振荡模态,保证实验结果的真实性,分析所选试点地区的电力系统基本情况。根据技术人员的现场实践与大量勘察,本次研究的电力系统为4 机双区系统,由A、B 这2 个区域构成。试点地区电力系统的基本结构如图1 所示。

表1 4 机2 区电力系统基本参数
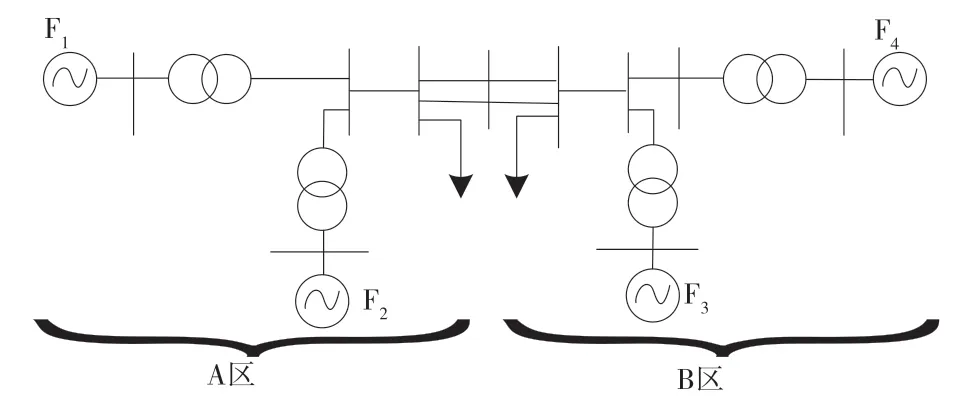
图1 试点地区电力系统基本结构
掌握试点地区电力系统的基本情况后,使用文章设计的方法对系统在运行中的低频振荡模态进行识别。通过对低频振荡频率、振型的识别,完成设计方法在此次研究中的应用。
在此基础上,引进基于Stein 的无偏风险估计(Stein's Unbiased Risk Estimator,SURE)小波消噪的辨识方法、基于调速侧电力系统稳定器(Governor Power System Stabilizer,GPSS)附加阻尼控制的辨识方法作为传统方法1 与传统方法2。使用3 种方法进行系统振荡模态的辨识,辨识结果如图2、图3、图4 所示。
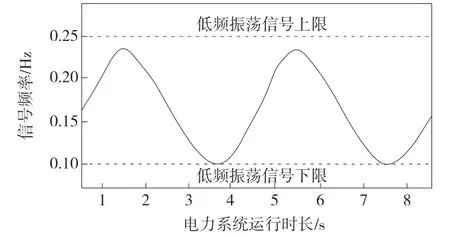
图2 本文方法辨识结果
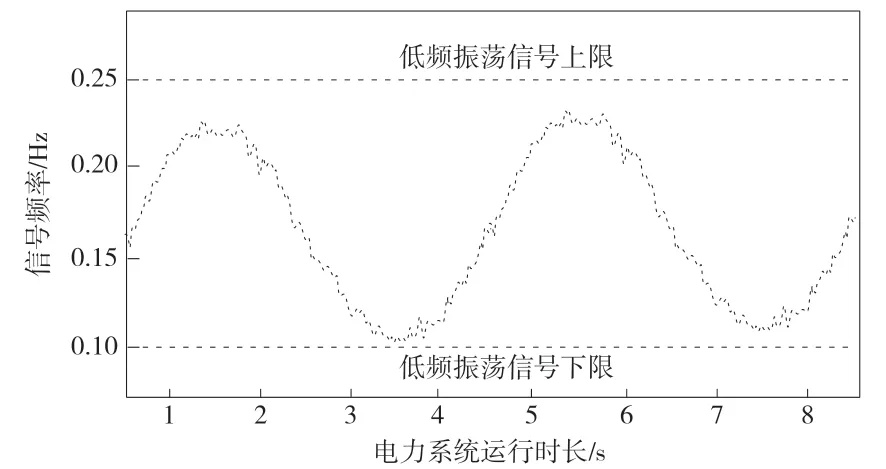
图3 传统方法1 辨识结果
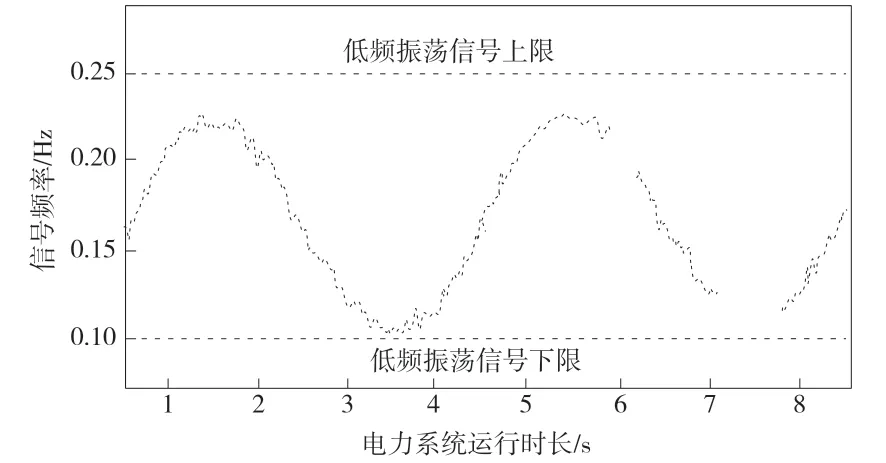
图4 传统方法2 辨识结果
由实验图像可知:使用本文方法辨识的系统低频振荡信号曲线平滑、完整、连续,可以将其作为判断系统运行存在低频异常的主要依据;使用传统方法1 辨识的系统低频振荡信号完整、连续,但信号曲线的平滑度较差,即辨识的结果携带一定的噪声,可能会影响系统低频异常的判决结果;使用传统方法2 辨识的系统低频振荡信号不仅连续性与完整性较差,而且信号的平滑度也较差,辨识结果携带噪声,无法作为判决系统运行状态。
通过对比实验,初步证明了文章设计的辨识方法在实际应用中的可行性。在此基础上,开展3次实验,明确系统在不同模态下的阻尼系数与振荡频率,实验结果如表2 所示。

表2 不同方法对系统模态的辨识结果
从表2 可以看出,本文方法的辨识结果与真实结果差值最小,而使用传统方法辨识的系统振荡频率、阻尼系数与实际值差值较大。相较于传统方法,考虑可控负荷接入的系统模态辨识方法在实际应用中的效果良好,该方法可以避免辨识结果携带噪声,提高电力系统运行振荡频率与阻尼系数辨识的精确度。
5 结 论
低频振荡会抑制电力系统的输电容量,如果未及时采取有效的措施对其进行处理,不仅会影响电力系统的输配电,还会诱发严重的电力安全公共事件。为解决此类问题,通过电力系统自由振荡响应信号提取、电力系统振荡模态信号分解、低频振荡频率与振型识别,在考虑可控负荷接入的条件下,设计模态辨识方法。经过对比测试,该方法在避免辨识结果携带噪声的基础上,提高了对电力系统运行振荡频率与阻尼系数辨识的精确度,具有较好的应用价值。
