基于深度强化学习的平滑车速控制系统
2023-09-02徐延军陈建雄
徐延军, 陈建雄
1.中远海运科技股份有限公司, 上海 200135;2.上海船舶运输科学研究所有限公司, 上海 200135)
0 引 言
近年来,随着汽车保有量的不断增加,高速公路上的交通拥堵情况越来越多,为提升高速公路的车辆通行效率,通常会对其出入口进行控制,因此高速公路上的交通拥堵路段比较固定,一般在主线与出入口匝道连接处、道路施工区域和交通事故发生处。当某路段出现交通拥堵情况时,车辆会频繁地进行变速、分流、合流和交织等,严重影响着其他车辆的通行。
平滑车速控制主要是对公路的交通流参数进行动态检测,将获取的交通信息输入控制器中,通过算法计算得到限速值,并将其反馈到限速板上,从而实现对车辆行驶速度的动态控制,在提升车辆通行效率和通行安全性方面有显著效果。在开展平滑车速控制研究时,需建立交通流仿真模型,其中METANET模型和元胞传输模型(Cellular Transmission Model)在平滑车速控制中的应用最广泛。CARLSON等[1]在反馈式控制系统中植入METANET模型,测试结果表明该模型能对系统的交通流参数变化情况进行仿真;HADFI等[2]提出一种改进的随机元胞模型,该模型充分考虑了车辆路径选择行为。此外,需在交通流仿真模型的基础上设计相关控制算法。ZHU等[3]基于R-马尔可夫平均奖励技术(R-Markov Average Reward Technology,R-MART)的强化学习算法获取最优限速方案,对路网中的车流量、时延时间和车辆排放等指标进行优化,与非限速控制相比,总行驶时间和一氧化碳排放量分别减少了约18%和20%;LI等[4]提出了一种基于Q-学习算法的限速值控制策略,该策略在稳定交通需求的情境中使车辆通行时间缩短了49.34%,在波动交通需求的情境中使车辆通行时间缩短了21.84%。本文以CTM为基础进行交通流仿真,在平滑车速控制系统中引入DDQN(Double Deep Q-Network)算法,对路段瓶颈区域进行平滑车速控制,以提升车辆通行效率,改善公路上的车辆运行情况。
1 交通瓶颈与控制理论
1.1 高速公路交通瓶颈
1.1.1 交通瓶颈区域的定义
高速公路瓶颈区域是指路网中易发生拥堵的路段,该拥堵问题通常是因突发交通事故、自然灾害致使道路损坏、道路施工和车辆在行驶过程中分流与合流等情况导致车辆的通行能力下降引起的。
1.1.2 瓶颈区域常见类型
交通瓶颈区域是影响整个路网车辆通行能力的关键因素,类似于木桶理论中的最低档板。以交通拥堵问题的发生频率为分类依据,可将交通瓶颈分为常发性交通瓶颈和偶发性交通瓶颈[1],其中:常发性交通瓶颈主要集中在主线与匝道衔接处,是因车辆在此处出现合流、分流或加减速行为而引发的拥堵状况;偶发性交通瓶颈主要集中在高速公路施工区、自然灾害破坏区或交通事故发生处,一般是占用车道引起通行能力下降造成的拥堵状况。[1,5]高速公路瓶颈区域主要可分为以下几种。
1) 主线与入口匝道衔接处(见图1)。在主线上游的车辆从A行驶至B过程中,支线车辆从入口匝道C经过加速区并入主线行驶,因此在匝道附近会出现合流现象,当主线上的车流量较大时,从入口匝道进入主线的车辆会使主线上的其他车辆频繁地减速或变换车道,从而导致道路的车辆通行能力下降。
2) 主线与出口匝道衔接处(见图2)。在主线上游的车辆从A行驶至B过程中,部分车辆会变道进入减速区,最后驶入出口匝道D,离开主线,因此在匝道附近会出现分流现象,当主线上的车流量较大时,想要汇入出口匝道减速区的车辆的行为会影响主线上正常行驶的车辆,从而导致道路的车辆通行能力下降。
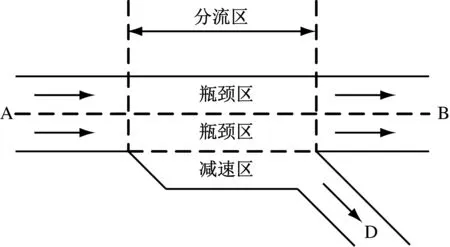
图2 出口匝道衔接处示意图
3) 施工/事故区(见图3)。在主线上游的车辆从A行驶至B过程中,当存在道路施工或发生交通事故时,一些车辆会临时占用部分车道,使具备通行能力的车道数减少,当上游的车流量较大时,这些车辆在行驶至此处时会来不及行驶到下游,从而导致道路的车辆通行能力下降。

图3 施工/事故区示意图
1.2 高速公路控制策略
为缓解瓶颈区域的交通拥堵状况,一般采用匝道控制和平滑车速控制2种方法[6]。
1.2.1 匝道控制
当出现恶劣天气或严重的交通拥堵现象时,外部车辆不再适合进入主线行驶,可临时关闭匝道,这种策略能较好地提升主线的通行能力,但会在很大程度上影响车辆的行驶路线,并使城市路网的交通压力增大[7]。另一种匝道控制方式是设置交通信号灯,周期性地控制匝道出入口的车流量。
1.2.2 平滑车速控制
平滑车速控制是指通过在道路上布设的传感器和摄像头等设备实时检测道路的交通运行环境,根据检测到的信息实时调整情报板上的限速值,从而使车辆能安全平稳地通过交通瓶颈区,进而减少交通拥堵现象。同时,通过速度控制能减少交通事故的发生,保障高速公路上车辆通行的安全性[6]。
1.3 平滑车速控制的必要性
平滑车速控制在提升车辆通行效率方面具有良好的效果。高速公路上的车辆在瓶颈区域会遇到拥堵现象,甚至是排队现象,此时拥堵状况会蔓延至上游路段,从而影响整个道路的运行情况,若不及时采取控制措施,道路会进入瘫痪状态。因此,在道路出现拥堵现象之前,通过平滑车速控制缓解瓶颈区域的车流量,从而尽可能地避免出现拥堵现象。
此外,平滑车速控制能提升车辆行驶的安全性。若跟车行驶的车辆之间的距离很小,当前车的驾驶员因某种突发状况而紧急刹车时,后车很容易因操作不及时而发生追尾事故,此时若不能及时控制,二次事故发生率会大大提升。对车辆进行平滑车速控制能有效控制其行驶速度,减小车辆间的速度差,平滑交通流,从而防止追尾事故的发生[7-8]。
2 系统的设计与实现
该系统采用数学模型对交通流演化规律进行精准表达,将平滑车速控制问题转化为最优求解问题,基于DDQN算法对最优限速值进行实时求解。根据实际交通运行状态与期望运行状态之间的偏差对限速值进行调整,以使快速路瓶颈路段内的交通流运行状态维持在其通行能力附近。该基于DDQN算法的平滑车速控制系统流程图见图4。

图4 基于DDQN算法的平滑车速控制系统流程图
2.1 系统功能模块
该系统根据事故风险和拥堵程度确定动态限速启动的阈值,根据道路上是否有特殊事件发生将限速值确定方式分为2种:若有特殊事件发生,则选择预设的限速方案;若无特殊事件发生,则采用DDQN算法对最优限速值进行实时求解。该系统主要包含动态限速启动模块、限速值确定与更新模块和情报板动态发布模块等3个模块,见图5。

图5 基于DDQN的平滑车速控制系统功能模块图
2.1.1 动态限速启动
根据当前的交通状态实时预测事故风险和道路拥堵程度,由此反映道路的车辆通行能力。当通行能力下降到标定的阈值时,启动上游的平滑车速控制策略,实现主动进行交通控制。
2.1.2 限速值确定与更新
若已发生特殊事件(包括交通拥堵、事故和恶劣天气等),则选择预设的限速方案;若尚未发生特殊事件,为避免事故发生,当预测事故风险值大于阈值时,通过预测不同限速值下的交通状态预测事故风险,事故风险较小和道路通行能力较强时的限速值即为最优限速值。避免限速时间过长,以免无法响应交通状况的变化;同时,避免限速时间过短,以免限速控制效果较差。此外,避免短时间内连续切换限速值影响驾驶员的安全行驶,限速值更新步长一般取10 min为宜。
2.1.3 情报板动态发布
通过可变情报板及时发布更新的各路段、各车道的限速值,及时影响驾驶员的驾驶行为,保证动态限速措施的实施效果。
2.2 深度强化学习算法
将深度学习与强化学习结合起来即为深度强化学习,其中DDQN算法是常见的深度强化学习算法之一,由最基础的Q-学习算法改进而来。深度强化学习算法主要依靠状态集、动作集、回报函数和学习参数实现,目标网络和经验回顾是其2个重要特性,能显著提升算法的性能[9]。经验回顾是指将样本数据储存起来,每次迭代学习时,从记忆池中随机选取样本对实时神经网络进行训练,以更新参数θ,降低样本的自相关性。经验回顾能使样本重复利用,从而提高学习效率。在从记忆池中取样时,采用优先经验回顾方法,其核心是在取样时优先选择可能取得更好学习效果的样本[10]。TD(Temporal Difference)误差能用来估计样本可能取得的学习效果,因此采用TD误差计算样本被选取的概率,各样本被选取的优先级pi的计算公式为
pi=|δi|+c
(1)
式(1)中:δi为TD误差;c为大于0的常数。为保证δi=0的样本依然有概率被选取,令δi的计算公式为
δi=Yi-Q(si,ai;θi)
(2)
式(2)中:Yi为目标值;si为状态;ai为动作;Q(si,ai;θi)为通过实时神经网络θi计算的Q值。Yi的计算公式为
(3)
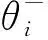
样本i被选取的概率p(i)的计算公式为
(4)
式(4)中:k为从记忆池中选取的样本量;α为优先程度,α=0表示均匀采样。
由于采用优先经验回顾方法会产生修正误差,因此在更新神经网络参数时,需采用IS权重(Importance-Sampling Weights)更新方法,其表达式为
(5)
式(5)中:θt和θt+1分别为神经网络在t时刻和t+1时刻的参数;ωi为经验样本i的IS权重。ωi的计算公式为
(6)
式(6)中:N为经验池中的经验样本总数;β为优先经验回顾的优先取样概率。
通过以上训练,使神经网络逐渐收敛,并计算出Q值,智能体在每种状态下都会选择Q值最大的动作,即最优动作,在该环境中采取最优控制策略。
2.3 基于DDQN算法的平滑车速控制策略
相比传统的Q-学习算法,DDQN算法能加入更多的状态变量,更准确地感知交通状态,并通过神经网络的方式计算状态-动作对的Q值[11]。此外,交通数据中不可避免地会含有数据噪声,引发过优化问题。DDQN算法通过采用不同的值函数对Q值动作进行选择和计算解决过优化问题[12]。因此,基于DDQN算法的平滑车速控制策略能取得更佳的控制效果,该控制策略框架图见图6。

图6 基于DDQN算法的平滑车速控制策略框架图
基于状态si使DDQN智能体感知高速公路的运行状态;针对当前的状态选择动作ai(限速值),通过该动作的变换促使当前的交通流运行状态转移到新状态,并计算该动作导致的交通流状态变化对应的奖励值ri+1;将这一步训练的数据作为经验样本存储到记忆池中,神经网络不断利用记忆池中的样本进行训练。[9]针对每个状态动作配对重复上述学习过程,随着神经网络的不断收敛,智能体会不断选择最优动作,使累计奖励值最大,即确定最优限速值。
根据平滑车速控制策略的实际应用场景,需确定深度强化学习算法的关键参数,具体如下。
1) 状态s。一般通过在路网中布设的检测器采集关键交通数据,主要包括瓶颈区的车辆密度、控制区的车辆密度和上个控制周期的限速值。瓶颈区的车辆密度为平滑车速控制中的被控制量;控制区的密度体现开展平滑车速控制时的交通运行状况;加入上个控制周期的限速值防止限速值变化幅度过大影响驾驶员的判断,从而使道路的事故风险增加。
2) 动作a。动作a为平滑车速控制区的限速值,本文的动作集为{5,10,15,…,80},共有16个动作,高速公路作业区的限速标准以安全通过为标准。
3) 奖励值r。控制策略的目标是缩短整个瓶颈区内车辆的总通行时间,将时间分为n个时长为μ的区间,此时总通行时间的计算公式为
(7)
式(7)中:T为总出行时间;N为瓶颈区内的初始车辆数;q(i)为在时间i时进入瓶颈区的车辆数;s(i)为在时间i时离开瓶颈区的车辆数。由交通流理论中车辆密度与车流量的关系可知,车辆密度过大或过小都会使车流量无法达到最大值,只有当车辆密度取某一合适值时,车流量才能达到最大,将该车辆密度称为最佳车辆密度。因此,平滑车速控制策略的奖励值根据瓶颈区的车辆密度确定,车辆密度越接近最佳车辆密度,奖励值越大。
4) 神经网络。该策略存在实时神经网络和目标神经网络,通过训练之后,对于特定的状态,利用神经网络能准确计算出限速值对应的Q值,智能体会直接选取Q值最大的限速值,即最优限速值。
5) 动作选择策略。DDQN智能体采用ε-greedy算法选择限速值,即根据ε概率随机选择限速值,根据1-ε概率选择Q值最大的限速值,因此收敛速度取决于ε的大小。在训练开始时,ε的值会比较大,以保证能充分搜索,随着训练的进行,ε会逐渐减小,一旦找到最优的限速值,就可一直选择该限速值。
2.4 仿真试验过程
2.4.1 仿真模型
平滑车速控制策略在实际应用之前需经过测试,由于在实际场地进行测试的周期较长,费用较高,且事故风险较大,一般采用交通流仿真模型对控制策略进行测试。本文采用最具代表性的元胞传输模型[13],由于该模型未考虑基于深度强化学习算法的平滑车速控制策略,因此引入新的变量和参数对其进行修正,建立高度还原实际交通流,并整合平滑车速控制策略的交通仿真模型。平滑车速控制策略下的交通流基本图见图7,假设交通参与者对限速值的遵从度为100%,则基本图左支的斜率即为限速值VSL。当左支的斜率发生变化时,交通流基本图的顶点位置会发生变化,即最大流量变小,密度变大,限速值VSL下的最大流量为QVSL,最大密度为dVSL。因此,根据平滑车速控制策略下的交通流基本图可得元胞的发送能力σ(t)和接受能力δi(t)的计算公式分别为

图7 平滑车速控制策略下的交通流基本图
σ(t)=min{VSL(t)·d(t)·n,QVSL}
(8)
δi(t)=min{w·(dj-d(t))·n,QVSL}
(9)
当无平滑车速控制策略时,元胞内的车辆平均速度由自由流速度和车辆密度决定。当有平滑车速控制策略时,各元胞内的车辆平均速度由限速值和车辆密度共同决定,具体计算公式为
(10)
采用以上计算方法即可基于元胞传输模型仿真平滑车速管控策略下的交通流运行情况。
本文选取宁夏高速公路某3 km长的路段作为研究对象,该路段的主线为4车道,路段内含有1个入口匝道、1个出口匝道和6台线圈检测器。线圈检测器采集的数据主要有速度、流量和占有率。该路段的瓶颈区域主要位于匝道处,采用CTM仿真从入口匝道汇入主线合流区域的车流量,仿真数据来自于设置在入口匝道处的线圈检测器,截取24 h的交通流数据。
2.4.2 DDQN智能体的训练过程
从记忆池中选择部分训练样本对神经网络进行训练,本文将训练过程划分为多个训练小节,在每小节中都需先将仿真路网初始化,然后仿真24 h的交通运行情况,以此循环。平滑车速控制的周期为10 min,训练过程一直持续到算法收敛,共经历150个训练小节,包含21 600个控制周期。训练场景的交通流量需求由路网实际需求设计得到,路网主线的实际交通流量需求为3 300~6 800辆/h,路网入口匝道的实际交通流量需求为280~700辆/h,训练场景中的路网交通流量需求见图8,波动较大,为在训练中能尽可能多地遇到各种交通状态。
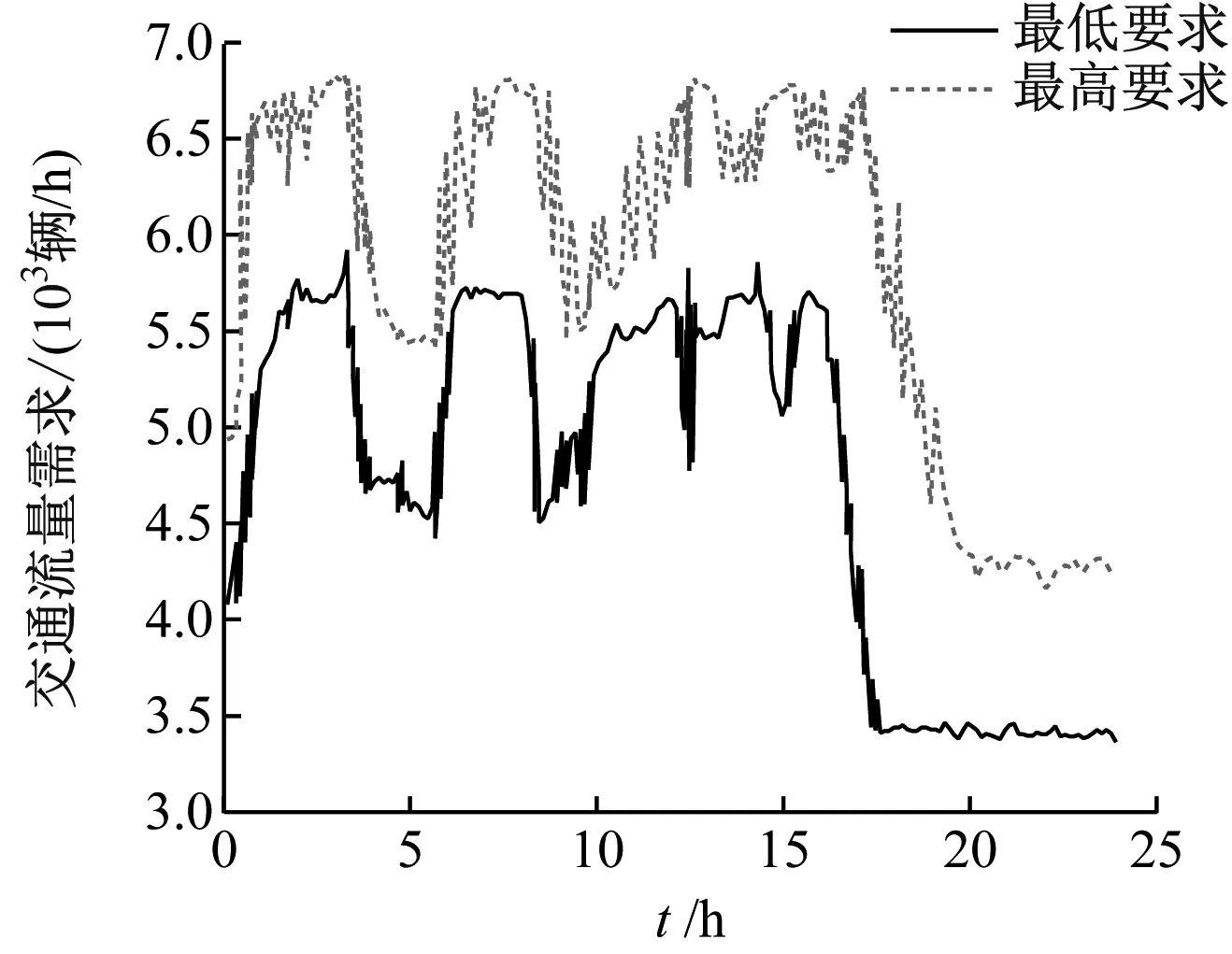
a) 主线交通流量需求

图8 训练场景中的路网交通流量需求
本文的神经网络结构由1个输入层、1个输出层和1个隐藏层组成,其中隐藏层有20个神经元,神经网络的参数设置见表1。优先经验回顾方法的参数设置见表2。β在前500步中从0.4线性递增至1.0,之后保持不变,β=1.0代表优先经验回顾的优先取样概率被完全抵消;ε在前500步中从 0.7 线性递减至0.1,之后保持不变。

表1 神经网络的参数设置

表2 优先经验回顾方法的参数设置
DDQN智能体在每个训练小节中取得的平均奖励值直接体现训练效果的好坏,平均奖励值越大,说明训练效果越好,DDQN智能体在训练过程中取得的平均奖励值见图9。DDQN智能体的平均奖励值在前90个训练小节中波动较大,在第90个训练小节左右达到最大,并在之后保持稳定。

图9 DDQN智能体在训练过程中取得的平均奖励值
2.5 平滑车速控制策略效果
为验证基于深度强化学习算法的平滑车速控制系统对道路车辆通行效率的影响,在仿真环境中对训练好的DDQN智能体进行测试,改变路网的交通流量需求,用车流量反映交通运行情况,不限速、固定限速值(60 km/h)和平滑车速控制等策略下的交通运行情况见图10,根据式(7)计算得到的瓶颈区内车辆总通行时间见表3。
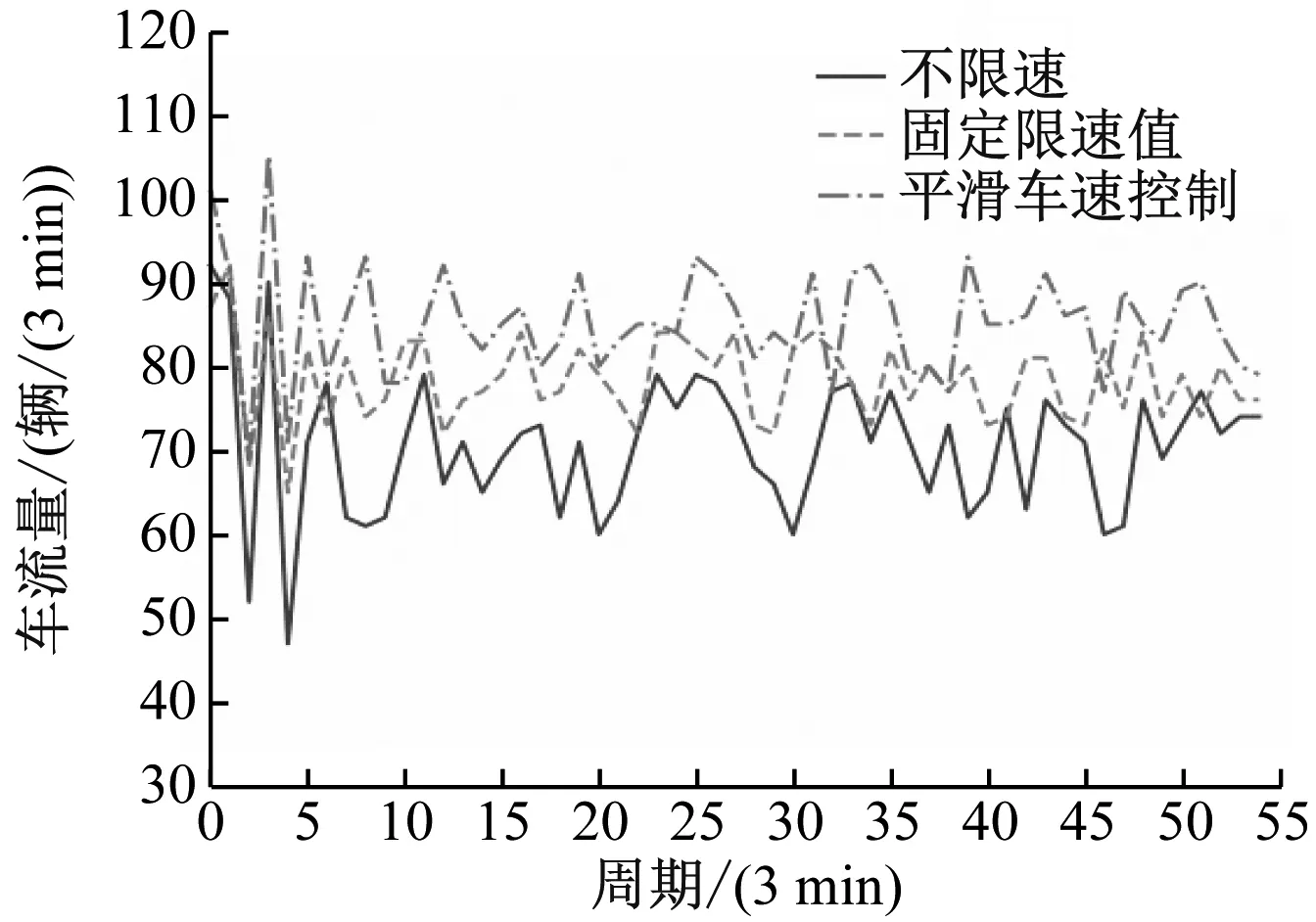
图10 不同控制策略下的交通运行情况

表3 不同控制策略下的瓶颈区内车辆总通行时间计算结果
综上所述:在平滑车速控制策略下,瓶颈区内车辆的总通行时间明显减少;不同控制条件下路段内的车流量均在某个区间内上下波动,但平滑车速控制策略下的区间明显大于其他策略,具有较好的控制效果。
3 结 语
在高速公路车速控制方面,对平滑车速控制进行研究具有重要意义,针对高速公路交通瓶颈区合理准确地确定限速值,能提升道路的车辆通行效率和通行安全性。本文设计并实现了基于深度强化学习算法的平滑车速控制系统,并在仿真环境下对其有效性进行了验证,效果良好,能在未来的道路交通瓶颈区推广应用。
