异型无人机空战对抗协同机动决策研究

2023-08-31牛军锋甘旭升魏潇龙吴亚荣

指挥与控制学报 2023年3期

牛军锋甘旭升魏潇龙吴亚荣杨芮

无人作战飞机（unmanned combat aerial vehicle,UCAV）作为未来空战的重要角色,实现其空战过程智能化是各军事强国研究的关键方向[1].美国作为航空和人工智能技术最发达的国家,在无人作战系统的研究上同样走在世界最前沿.早在2016 年,美国的智能空战模拟系统便能以100%的概率战胜退役的空军上校[2].2017 年3 月,美国空军与洛·马公司基于无人化的F-16 对“忠诚僚机”概念关键性技术展开验证,包括开放式系统架构的软件集成环境和无人机的自主任务规划功能,旨在实现有人机与无人机的协同作战[3-4].在美军的2013 版《无人机系统综合路线图》中,更是计划到2030 年前后实现无人机编队的自主协同侦察与攻击功能.因此,我国同样应当加大无人作战飞机自主决策技术的研究,否则难以在未来的空战场上取得优势.

无人机协同空战对抗既涉及空中的自主避撞,又涉及战术的协同机动决策,相对单机对抗和同型机协同机动决策具有更大的技术难度和复杂度.从国内外的研究现状来看,主要仍基于同机型的对抗决策或协同机动决策研究,对于异型机之间的协同机动决策还仍有不足.NGUYEN 使用线性二阶模型构建无人机编队模型,使用一致性理论设计集群的编队控制算法[5],但该研究主要关注动目标的协同追踪问题,对于更复杂的协同控制决策则并没有涉及.ZHEN 提出了一种智能自组织算法[6],该算法可实现多无人机对抗的目标分配问题,主要方法是将全局问题分解为局部问题并进行优化计算.但该研究主要关注对地目标的协同攻击,态势相对简单.朱星宇基于Q-Learning 算法构建无人机的机动决策模型[7],而无人机之间的协同目标分配则是使用纳什均衡理论,由此实现多无人机空战机动决策.研究中既考虑了冲突解脱问题,也考虑了态势问题,具有较好的参考价值.魏潇龙基于改进蚁群算法研究了无人机的自主冲突解脱问题[8],具有一定参考价值.

本文对异型机之间的空战协同决策问题展开研究,主要分析电子干扰无人机与空战无人机之间的自主协同决策方法.在探讨电子干扰伴随支援战术机动方法基础上,基于一致性理论设计了无人机之间的编队控制方法,使用蚁群算法实现我方无人机之间的冲突解脱与战术机动,使用改进的Q-learning算法设计敌对无人机的空战机动决策算法,最后通过空战仿真验证协同机动算法的有效性.

1 异型无人机协同空战环境建模

1.1 异型无人机协同战法描述

同型机之间的空战协同对抗主要是通过长僚机之间的协同空中战术机动,积极构成我方攻击态势上的优势,并使敌机陷入战术被动,实现战损比的最大化.在这过程中,长僚机均为攻击主体,目的都是为了使用火控雷达锁定敌机,并构成导弹发射条件.异型机的协同空战对抗则有明确的任务分工,由攻击型无人机担负制空作战任务,伴随机则提供一定支援力量.根据无人机性能的不同,无人机提供的力量支援也有所不同,本文主要探讨电子干扰无人机作为僚机时的协同制空作战情景.

电子干扰无人机在与歼击无人机协同作战过程中,主要位于空战区域的后方提供电子干扰支援,通过阵位的变换使自己处于较为安全的境地,使敌机处于电子干扰范围之内,降低其作战效能,提高己方战损比.歼击无人机在作战过程中应当积极占据有利态势,将敌机置于火控雷达照射之下,避免自身被敌方火控雷达锁定.在无人机的协同对抗过程中,还应当兼顾任务编组之间的防相撞问题.由于歼击无人机需要优先执行制空作战任务,态势争夺异常激烈,因此,编组间的冲突解脱可由电子干扰无人机通过主动的机动避让实现.编队战术机动方法如图1 所示.

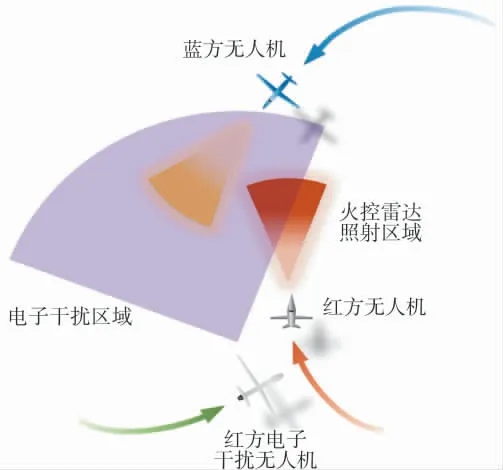
图1 异型无人机编组战术机动方法Fig.1 Tactical maneuver method of special shaped UAV formation

为便于论述,本文将我方无人机称为红方,敌方无人机称为蓝方.图1 中,红方电子干扰无人机机动至歼击无人机后方阵位,并对蓝方施加电子干扰,通常电子干扰范围大于火控雷达照射范围.红蓝方无人机都积极通过机动动作绕开对方火控雷达,并伺机锁定对方发射导弹.但在判明蓝方无人机处于电子干扰状态下时,红方无人机即可采取激进的攻击策略,直接对向蓝方无人机飞行,并实施火控雷达锁定.无人机战术机动决策流程如图2 所示.

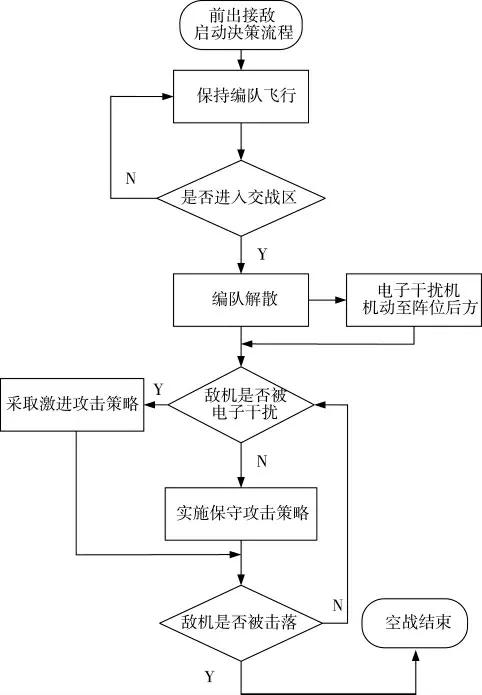
图2 无人机战术机动决策流程Fig.2 UAV tactical maneuver decision-making process

1.2 态势判断准则构建

红蓝双方对态势的判断主要基于相对角度和距离要素.存在的态势类别主要有锁定、被锁定、相互锁定、干扰和被干扰.几何关系如图3 所示.

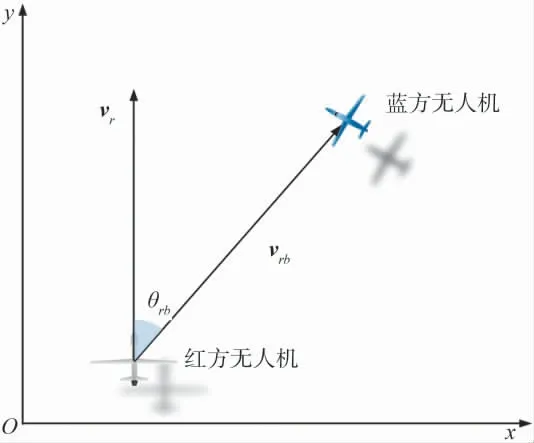
图3 态势判断几何关系图Fig.3 Geometric relationship diagram of situation judgment

图3 中,vr为红方无人机的航向向量；vrb为红方无人机指向蓝方无人机的向量.红蓝方无人机的相对距离是态势判断的第一要素,也是本文实施战术转换的判断依据,基本计算方法为：

式中,（xr,yr）为红方的大地坐标；（xb,yb）为蓝方的大地坐标.当红方无人机与敌机相对距离大于lf时,则认为处于交战区外,红方无人机继续保持编队飞行前出接敌.当红蓝方无人机相对距离小于lf时,则红方无人机编组开始变换阵位,实施制空作战.制空作战过程中,需要根据距离和相对角判断锁定、被锁定、相互锁定、干扰和被干扰等态势.相对角计算方法为：

式中,vr为红方无人机的航向向量；vrb为红方无人机指向蓝方无人机的向量.当相对角θrb小于红方的火控雷达照射角θrf,且相对距离小于火控雷达作用距离df时,蓝方处于红方火控雷达锁定状态.其他态势的判断方法与此类似,文中不再赘述.

基于敌我态势构建态势判断矩阵,可表示为：

其中,在红方无人机火控雷达能够照射蓝方无人机时e11=1,否则为0,计算方法为：

式中,θrf为红方无人机火控雷达的照射角度范围；drf为红方火控雷达的照射距离.当红方电子干扰机对蓝方成功实施电子干扰时,e21=1,否则为0,计算方法为：

1.3 动态栅格环境搭建

对无人机机动决策指令的生成主要基于路径规划的方法,需要有一定的栅格环境作为支撑.传统的栅格环境与大地坐标系相对固定,无人机在固定栅格环境内规划决策机动.但空战对抗具有极高的动态性和不确定性,敌机可能从多个方向突击重要目标,静态栅格环境如果覆盖广阔的区域则必然需要牺牲分辨率或者规划时间,从而影响决策准确性与效率.而且在飞机进行机动转场后,空域环境发生变化,静态栅格必须要重新校正和初始化,增加前期飞行准备的工作量.对此,设计了一种动态自适应的栅格环境,可确保规划空间的稳定性,如图4 所示.动态栅格环境完全不受限于敌我态势环境,分辨率始终根据敌我距离自适应调整,根据敌我位置旋转调整,只要不进入低空空域,动态栅格环境始终适用.若无人机进入低空空域,由于动态栅格不具备存储地面障碍物高度信息的能力,因此,规划栅格必须进行切换.

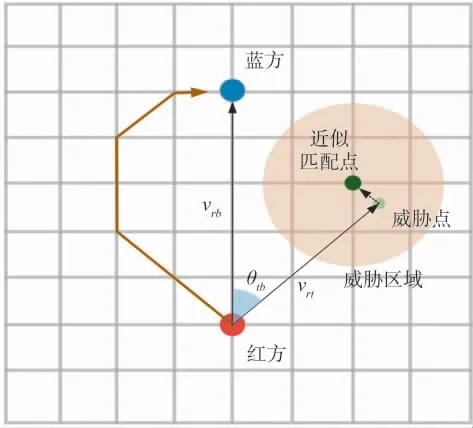
图4 动态栅格环境Fig.4 Dynamic grid environment

图4 中红方与蓝方在栅格中的位置固定,栅格单位尺寸根据红蓝方的相对距离自适应调整,计算方法为：

式中,N*为红蓝方栅格位置之间边的数量.图中的威胁点一般不在栅格节点上,因此,需要近似匹配至最近的动态栅格节点上,用以路径规划时避让.节点匹配计算方法为：

式中,（xt,yt）为威胁点近似匹配的栅格坐标；θtb为向量vr与vrb之间的夹角.此外,动态栅格以红蓝方无人机的相对位置不断旋转变换,因此,栅格点与大地坐标之间存在转化关系,转换公式为：

式中,（xg,yg）为任一栅格坐标；（x',y'）为对应的大地坐标；φ 为栅格坐标与大地坐标所成的角度；为无人机在栅格坐标中的位置向量与x 轴形成的夹角,规定逆时针旋转为正.

2 无人机飞行控制模型

在探讨红蓝方态势的争夺和机动策略的制定都基于侧向机动实现,且无人机在控制律的设计中水平方向与垂直方向可以相互解耦[9],因此,主要设计水平方向的控制模型,可表示为：

式中,a 为加速度,中括号内分别为变量的最小和最大值.同时,速度变量与航向之间有一定的转化关系,可表示为：

式中,vx,vy分别为速度沿横坐标与纵坐标的分量.由此可建立起指令信息与加速度、转弯率之间的转化关系.

3 异型无人机协同空战机动决策建模

3.1 一致性算法

讨论的无人机编组为双机编队,假设编队之间能够保持通信的持续不间断,则给出基本一致性算法为：

由此,可给出一致性的收敛条件[9，11]：

式中,μi为的第i 个特征值；Re（μi）和Im（μi）为μi的实部和虚部.根据以上定理,对于研究的无人机双机编队情景,其拉普拉斯判定矩阵为：

3.2 基于ACO 算法的机动决策

ACO 是一种典型的群智能搜索算法,具有仿生进化特性,常被用于解决路径规划问题,效果较好[8].ACO 具有随机搜索特性,智能体在每一个节点处根据周围可选节点的信息素浓度,按照轮盘赌的策略选择下一个节点,依次类推,直至到达终点.节点概率计算公式为：

式中,dj为节点j 至目标点的欧式距离.所有智能体在完成一次搜索之后,需要对全局信息进行一次更新,这也是智能体的自学习过程.学习的原理为加大较优路径的信息素浓度,其余路径则进行一次信息素蒸发.信息素更新公式为：

式中,F*和F 均为常数；L*和Lk分别为最优路径和排名为k 的次优路径的长度.在每一次的迭代完成后,都检查更新最优路径,在迭代完成后,输出最优路径.ACO 算法还设有禁闭表,对于表中的节点,智能体无法转移探索.将协同无人机及其安全范围内的节点均加入禁闭表,将敌对方的火控雷达照射范围内的节点也列入禁闭表,一方面可以减小搜索范围,另一方面可以实现冲突的解脱.在无人机进入交战区后,根据获得的态势信息选择进攻策略,初始化动态栅格的起点、终点、禁闭表和信息素,开启路径规划的迭代更新.最终输出的路径会为无人机提供向左、向右或直飞的机动决策信息,无人机在Δt 内按照决策信息调整飞行姿态.

3.3 基于Q-Learning 算法的机动决策

由于在实际空战过程中,敌我双方的武器平台总会存在性能差异,机动决策能力、原理、优势都不一致,因此,需要使用不同的决策算法模拟红蓝双方的机动决策行为.Q-Learning 算法是一种典型的机器学习算法,可以用于解决序贯决策优化问题[7],其数学基础为马尔可夫决策过程（Markov decision processes,MDP）理论[12].该算法属于离线策略下的表格型学习算法,最早由WATKINS 提出[13-14].Q-Learning算法的学习机制主要通过一张Q 表实现,表格中的行代表智能体状态,而列代表了能够采取的动作策略,通过对表格中元素的更新实现对外界环境的学习,更新方式为：

式中,σ 为学习率；ξ 为折扣因子；s 为当前时刻的状态；ac为当前时刻按策略π 采取的动作；s'为下一时刻的状态；ac'为在s'状态下能够获得最大回报的动作.智能体在状态s 时按照策略π 采取动作ac转移至状态s'.这一策略可以是随机准则、贪婪准则或ε-贪婪准则.在转移至新的状态后会获得一定的回报,可以是奖励,也可以是惩罚,根据获得的回报值按式（19）更新Q 表.智能体重复“转移—更新”这一过程,直到到达目标状态,完成一轮迭代,并准备开启下一轮迭代.在进行完一定次数的迭代后,Q 表中便积累了一定量的经验知识,智能体根据Q 表积累的经验知识按照贪婪准则形成最终的状态转移策略.具体流程如图5 所示.

图5 Q-Learning 算法流程Fig.5 Q-learning algorithm flow

但传统Q 表的初始状态为空白表,因此,在智能体的学习过程中存在学习效率低、探索不充分、易陷入局部最优的缺陷,特别是智能体探索过程中积累的大量无效信息不但耗费大量时间,而且容易使求解过程陷入局部最优.对此,提出一种双Q 表算法（double Q-learning table algorithm,DQLT）改进智能体的学习效率.DQLT 算法主要基于两张Q 表记录智能体的探索学习过程.需要对Q 表进行初始化,并加入启发式因子,计算过程为：

应当说明,DQLT 与Double Q-learning 算法在原理上有显著的不同.Double Q-learning 算法虽然使用两张Q 表进行学习探索,但主要是按照不同的遍历次序交替记录学习信息,可改善解的偏置问题.而DQLT 则并不是为了解决偏置问题,通过双Q 表的交替主要是为了剔除大量的无效学习信息,提高解的质量.DQLT 算法的空战机动决策建模与ACO 算法类似,同样是基于动态栅格环境,最后输出的也是左转、右转和直行指令.

3.4 电子干扰无人机机动决策算法

电子干扰无人机的机动决策需要解决3 个问题,分别是前出作战时编队的保持、伴随支援中与编队无人机的冲突解脱、根据态势变化的干扰阵位机动.无人机编队的保持主要基于一致性算法,由于飞行状态相对稳定,因此,机动决策过程较为简单.当任务编组进入交战区后,编队解散,电子干扰无人机需要转移阵位,并避免与己方无人机发生空中相撞.在这过程中主要基于ACO 算法进行路径规划,根据红蓝方态势调整阵位点,如图6 所示.

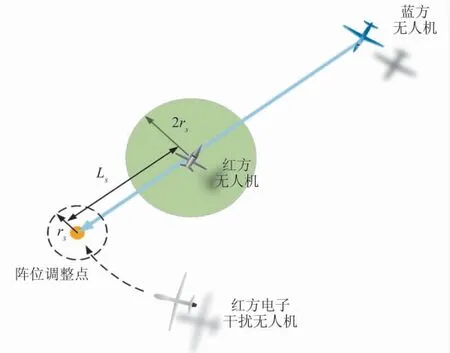
图6 电子干扰无人机机动决策方法Fig.6 Maneuver decision-making method of electronic interference UAV

图6 中,rs为无人机之间应对保持的最小距离.以歼击无人机为中心,构建2rs为半径的保护圈,当无人机距离阵位调整点距离大于rs时,无人机采用ACO 算法规划路径前往阵位调整点,机动过程中与歼击无人机保持2rs以上距离.当无人机进入阵位调整点半径rs范围内时,无人机使用一致性算法实施伴随干扰.阵位点的计算方法为：

式中,Lbe为电子干扰无人机与蓝方无人机应对保持的最小距离；drb为红方歼击无人机与蓝方无人机之间的距离；Lr为常数,且有.

4 仿真分析

为验证设计的协同空战对抗算法有效性,需要对一致性算法进行仿真验证.模型参数设置如表1所示.

表1 一致性算法参数设置Table 1 Parameters of consensus algorithm

基于一致性算法的长僚机编队汇集伴飞的过程如图7 所示.

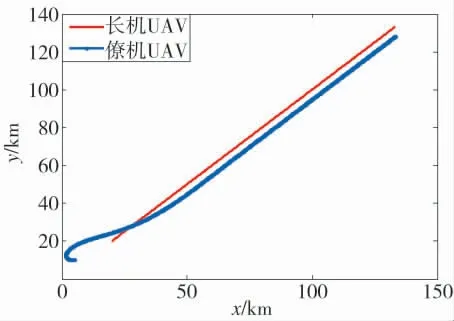
图7 无人机编队飞行航迹Fig.7 Flight tracks of UAV formation

航向变化过程如图8 所示.速度变化过程如图9所示.从图7～图8 可以看出,无人机能够快速调整航向汇合成指定队形飞行；图9 可以看出,由于初始时刻僚机落后于长机,因此,以大速度追赶,编队汇合后能够以一致的速度保持编队队形,说明了算法设计的有效性.再来验证基于改进ACO 和DQLT 算法的有效性,ACO 算法的参数设置如表2 所示.

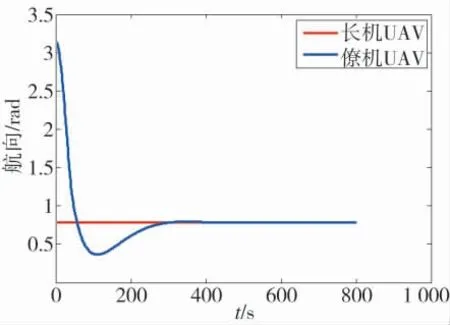
图8 无人机航向跟随过程Fig.8 Heading following process of UAV

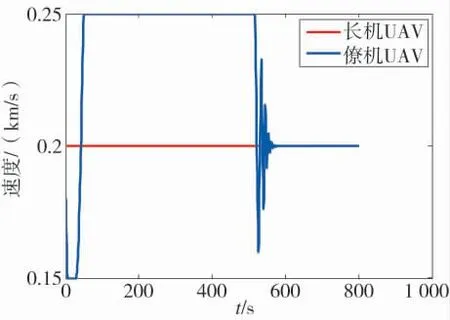
图9 无人机编队速度跟随过程Fig.9 Speed following process of UAV formation

路径规划效果如图10 所示.

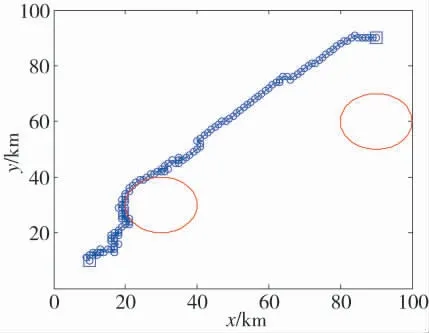
图10 基于ACO 算法的路径规划Fig.10 Path planning based on ACO algorithm

从图10 中可以看出,ACO 算法所规划路径并非严格最优路径,是一种近似最优路径.在动态的空战机动决策中允许低概率的错误决策出现,在规划时间足够的情况下,后续正确的决策可以及时纠正不良的决策机动.但决策的正确性显然是越高越好,因为这会使无人机能够更快、更好地抓住战机,锁定敌机.ACO 所规划的路径能够较好地避开栅格图中设置的威胁圈并抵达终点,将主要用于电子干扰无人机的机动决策和冲突解脱.

Q-Learning 算法主要用于歼击无人机的机动决策,直接在40×40 的动态栅格环境下测试Q-Learning算法的路径规划有效性.算法参数设置如表3 所示.

表3 Q-Learning 算法参数设置Table 3 Parameter setting of Q-Learning algorithm

由于基本算法学习率低,常常出现品质不佳的路径规划结果,如图11 所示,改进后算法的路径规划效果如图12 所示.

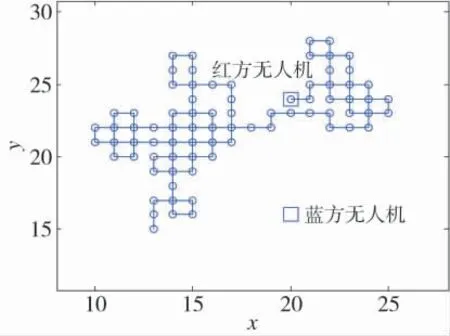
图11 Q-Learning 算法规划的路径Fig.11 Path planned by Q-learning algorithm

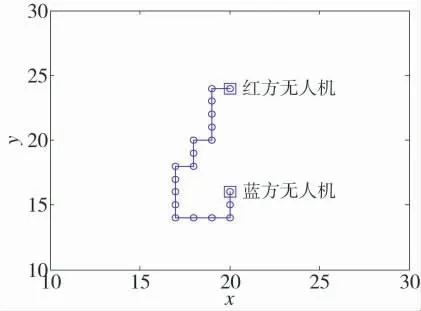
图12 改进Q-Learning 算法规划的路径Fig.12 Path planning by improved Q-learning algorithm

由于路径的节点数直接反映了路径的品质,因此,可以从每次路径规划的节点数指标来考察改进算法的有效性.另外,规划时间也是考察算法性能的一项重要指标.为及时终止失败的路径规划过程,算法设置了路径步长上限,当达到该值时,直接终止规划过程.将步长上限设为100,则规划性能对比如图13 所示.

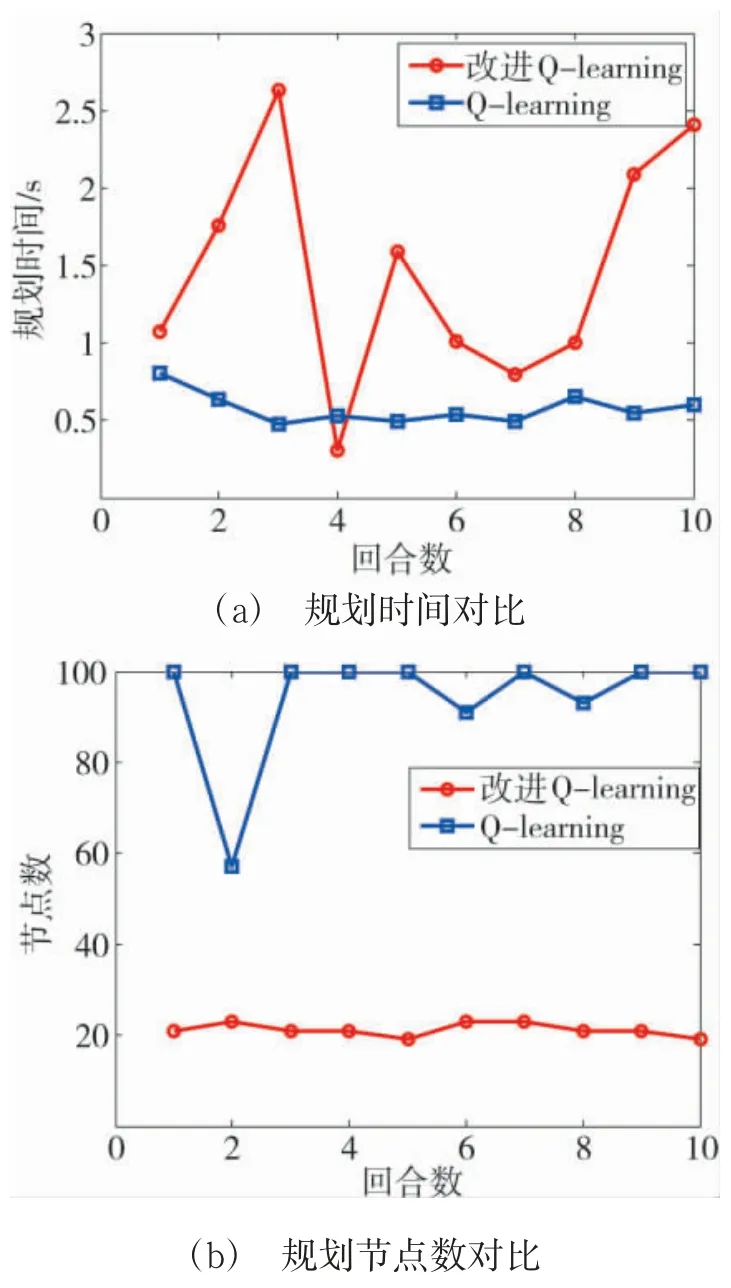
图13 改进Q-Learning 算法性能对比Fig.13 Performance comparison of improved Q-learning algorithm

从图13 中可以看出,改进算法路径品质显著优于基本算法,虽然规划耗时有增加,但仍在可接受的范围内.进一步的,可进行无人机空战对抗仿真.由于真实空战条件下,敌我双方无人机总会存在性能差异,因此,红蓝方的歼击无人机分别基于ACO 和Q-Learning 算法开展仿真,重点是验证红方无人机编队协同机动决策算法的有效性.在对抗空战过程中,并非使用火控雷达锁定即可取得胜利,导弹发射后击落敌机具有一定概率性,特别是在电子干扰条件下,这一概率还将降低,因此,需要设置不同态势下的攻击成功概率.具体可表示为：

式中,pr和pb分别为红方和蓝方歼击无人机在不同态势下的攻击概率值.在无人机锁定敌机后,每隔一个单位时间Δt,即有一定概率击落敌机,若击落成功则空战结束.蓝方无人机击落任意一架红方无人机同样判断空战结束.由于蓝方无人机为单机,因此,在对抗过程中以距离最近的无人机作为优先攻击目标.以红蓝方的单机对抗考察ACO 与改进Q-Learning 算法本身的决策品质,基本参数设置如表4 所示.

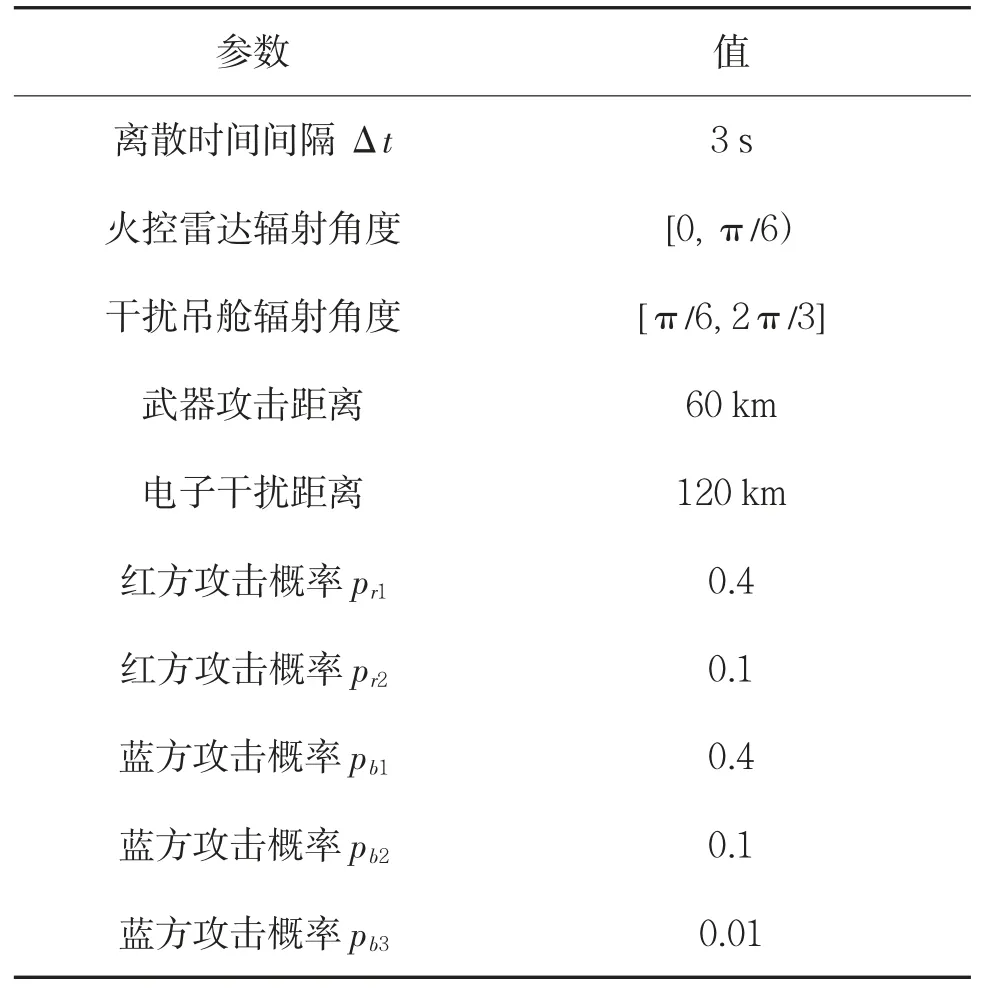
表4 空战对抗参数设置Table 4 Parameters of antagonistic air combat

空战仿真过程如图14 所示.

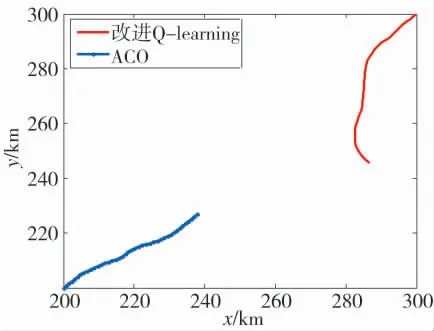
图14 无人机单机对抗空战过程Fig.14 Antagonistic air combat process of one UAV

图14 中,红方无人机在机动过程中被蓝方无人机击落.通过20 个回合的仿真可以进一步看出算法的决策品质,如图15 所示.

图15 单机对抗战损比Fig.15 Kill-death-assist of one UAV antagonistic combat

从图中可以看出,对于单机对抗,ACO 算法决策品质更好,能够更好地占据优势并击落敌机,战损比大约为3∶2,红方处于劣势.再来看加入电子干扰无人机后的空战仿真过程,如图16 所示.

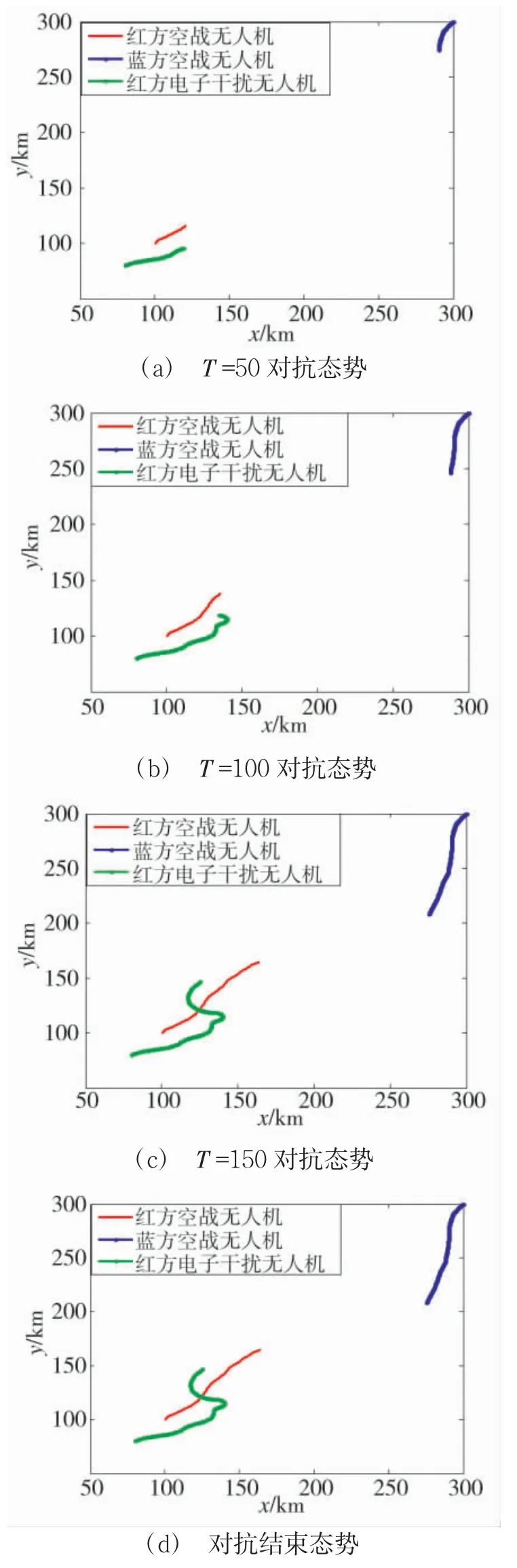
图16 无人机协同空战过程Fig.16 UAV cooperative air combat process

图16 中,红方仍使用改进Q-Learning 算法,蓝方使用ACO 算法,蓝方进入电子干扰机辐射范围,在躲避红方过程中被红方锁定击落.ACO 算法具有很强的机动决策能力,同样也能通过机动动作击落红方无人机,如图17 所示.

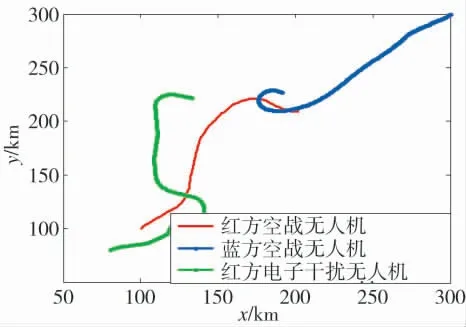
图17 红方无人机被击落过程Fig.17 The process of red UAV being shot down

图17 中,红方无人机未能成功锁定蓝方无人机并实施攻击,蓝方无人机趁机反向机动并击落红方无人机.加入电子干扰机后的红蓝方战损比如图18所示.

图18 改进Q-Learning 算法协同作战战损比Fig.18 Kill-death ratio of cooperative combat based on improved Q-Learning algorithm

从图18 可以看出,红方加入电子干扰无人机后,战损比有所提升,约为1∶1.为降低机动决策算法本身的影响,突显协同决策算法的有效性,红蓝方歼击无人机调换算法后再次考察战损比,如图19 所示.

图19 ACO 算法协同作战战损比Fig.19 Kill-death-assist of cooperative combat based on ACO algorithm

从图19 可以看出,基于ACO 决策算法的红方无人机战损比得到显著提升,约为9∶1.从图16 和图17 的仿真航迹中可以看出,电子干扰无人机能够较好地变换阵位提供伴随干扰的同时,对己方无人机进行规避,避免空中相撞的发生,同样验证了算法的有效性.从图18 和图19 的仿真结果中可以看出,设计的异型机协同决策机动算法有效,可提升单机无人机空战对抗的战损比.