考虑分区各向异性和渗流作用的边坡稳定性研究
2023-08-31张帮鑫贾剑青赖远明王宏图辛成平
张帮鑫 ,贾剑青 ,赖远明 ,王宏图 ,辛成平
(1.兰州交通大学 交通运输学院,兰州 730070;2.中国科学院 西北生态环境资源研究院,兰州 730000;3.重庆大学 资源与安全学院,重庆 400044)
土体强度的各向异性和渗流作用是影响边坡稳定性的重要因素[1-2];强度折减法是边坡稳定性分析的重要方法之一[3],近年来,学者们对此开展了一系列研究。苏永华等[1]建立了考虑土体含水率分布与坡面渗流作用的降雨入渗分析模型,并确定了边坡稳定性系数计算公式;Sun 等[3]提出了一种基于特征点位移突变的残差位移增量准则,将最大平均残余位移增量对应的强度折减系数作为边坡的安全系数;Rao 等[4]研究了非均质和各向异性黏性土边坡的抗滑桩加固技术和稳定性;Xu 等[5]探讨了非均质系数和各向异性系数与边坡体加固效果的关系;罗凌晖等[6]研究了土体强度各向异性对成层土边坡稳定性的影响,并结合强度折减法分析了其稳定性;曾铃等[7]试验研究了不同降雨条件下砂土和粉质黏土体积含水率与基质吸力的变化规律;Zeng 等[8]研究了降雨入渗条件下,边坡体内瞬态饱和区的形成、发展和消散过程;何晓莹[9]考虑渗流正交异性的耦合作用,研究了胶凝砂砾石坝的渗流及应力变化特性;王正成等[10]考虑弹性模量、泊松比等参数的变化,建立了流固耦合模型,分析了某坝基渗流场与应力场特征;史卜涛等[11]提出了物质点强度折减法,并分析了某边坡稳定性;Nie 等[12]研究了强度折减法的破坏准则,并与极限平衡法进行了比较;刘亚栋[13]分区考虑土体强度各向异性,计算分析了边坡稳定性,但该分区方法仅视觉性地将应力偏转方向大体一致的区域进行集中分区。目前,鲜有文献考虑土体分区各向异性和渗流作用对边坡稳定性的影响。笔者以某边坡工程为例,考虑土体分区各向异性和雨水的入渗作用,建立流固耦合模型,并采用强度折减法计算分析边坡稳定性。
1 流固耦合理论与强度折减法
1.1 流固耦合理论
流固耦合的基本思想是采用有限元方法将边坡体离散为有限个土体单元,并通过求解由达西理论和有限元理论所建立的有限元方程,即可得到单元体的节点位移和孔隙水压力,然后结合渗流场和应力场相互作用机理,推出两场耦合的有限元模型[14-15]。流固耦合中,渗流场影响应力场模型可表达为[14-15]
式中:k为渗透系数;σ和p为k的影响参数;H为形函数;q为 流量;n2为边界Γ2的法线 方向;n3为边界Γ3的法线方向。
应力场影响渗流场模型为[14-15]
式中:L为微分算子矩阵;n为面力边界Sσ法线方向的方向余弦矩阵,即为渗流场的水头分布函数;X为节点外荷载矩阵;{u}为位移场;B为应力插值矩阵;D为弹性矩阵;Sσ为已知面力边界;tˉ为已知面力边界Sσ上的面力分布,也为水头分布H(x,y)的函数;SM为位移边界;{uˉ}为位移边界SM上的位移矢量。
则流固耦合有限元模型为[14-16]
式中:K为渗透系数相关矩阵;{f}为渗流场水头分布函数;{H}为形函数;M为整体刚度矩阵;X为节点外荷载矩阵;F为渗透力矩阵。
1.2 强度折减法
强度折减法是在外荷载不变的情况下,将土体抗剪强度参数的黏聚力和内摩擦角进行折减,得到新的土体强度参数,并通过不断增大折减系数Fr直至边坡达到极限平衡状态,此时折减系数即为边坡体的安全系数,可表示为[15,17]
2 工程背景
研究的边坡位于陕西省咸阳市旬邑县境内,为中国国家高速公路菏泽至宝鸡联络线某合同段项目;边坡体地质构造为发育中、新生代陆相地层,地下水主要由降雨及周边河谷暗流组成;项目区地处内陆,年平均降雨量为589.4 mm。边坡横断面如图1 所示(为便于分析,下文图表中①为水泥土;②为素土;③为浅黄色粉土;④为黄褐色粉质黏土)。各土层物理力学参数如表1 所示。

表1 物理力学参数Table 1 The physical and mechanical parameters
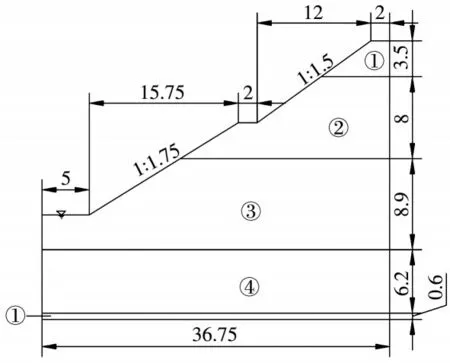
图1 边坡横断面图(单位:m)Fig.1 Cross-sectional view of the slope (Unit: m)
3 边坡稳定性分析
3.1 模型建立和参数确定
3.1.1 模型建立 建立的边坡有限元模型如图2所示。根据边坡成层土体地质分布特征并结合其几何形状,将边坡体划分为I 区、Ⅱ区、Ⅲ区和Ⅳ区4个区域。

图2 有限元模型Fig.2 Finite element model
流固耦合分析中,在模型gh边施加水平和垂直位移约束,fg和ah边施加水平位移约束,其他边均为自由边界;考虑降雨入渗的影响,在abcdef边施加降雨荷载,根据该地区年平均降雨量的统计结果,取雨水入渗强度为6.365×10-5m/h;在fghi区域内考虑孔隙水压力变化;模型网格单元类型选用孔隙流体单元(CPE4P)。
3.1.2 参数确定 土层抗剪强度参数会随土体最大主应力方向角α的变化而变化[14,18-19]。当角α分别为0°、30°、60°和90°时,取土体各向异性系数K=0.7,采用Casagrande 法[13]计算所得各土层的强度参数,如表2 所示。利用最小二乘法并结合表2,推导土体①、②、③、④各向异性强度参数方程,分别为式(5)、式(6)、式(7)、式(8)。
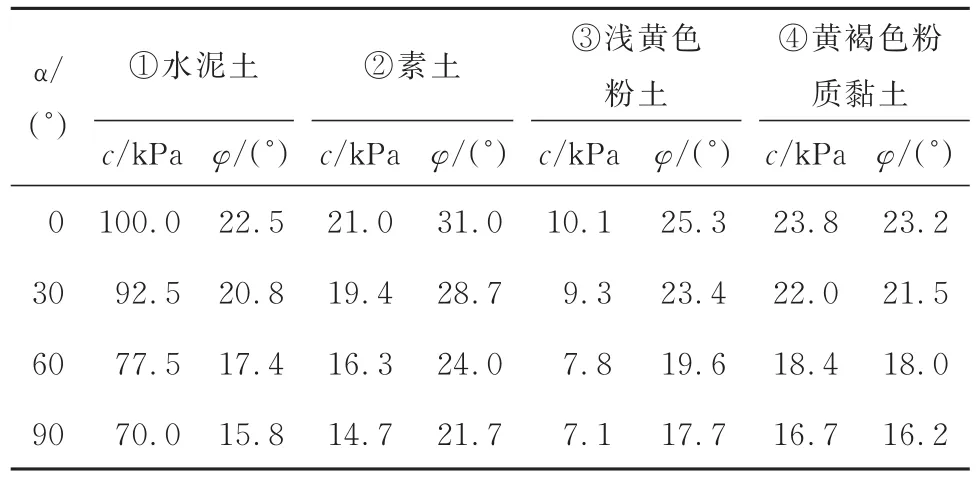
表2 抗剪强度参数变化Table 2 Variation of shear strength parameters
式中:Ac=-0.068 05×(1-3 cos2α) ;Aφ=0.061 32× (1-3 cos2α),Ac和Aφ分别为黏聚力和内摩擦角的各向异性状态参数;b为中间主应力参数[20-21];α为最大主应力方向角,对于平面应变问题,角α可通过式(9)确定[13],即
式 中:σx、σy和τxy分别为该单元在xy平 面内水平和垂直方向的正应力和剪应力;r表示应力Mohr 圆半径。
渗透系数随基质吸力的变化为[14-15,22]
式中:Kws为土体饱和时的渗透系数,取Kws=5×10-6m/s,即Kws=0.018 m/h;uw为土体中的水压;aw、bw和cw为材料系数,取aw=1 000,bw=0.01,cw=1.7。
饱和度随基质吸力的变化为[14-15]
式中:Sr为饱和度;Si为残余饱和度,取Si=0.08;Sn为最大饱和度,取Sn=1;as、bs和cs为材料系数,分别取as=1、bs=1.5×10-5、cs=3.5。
3.2 分级加载及分区方法
边坡初始应力状态对模型单元体最大主应力、最小主应力及剪应力等均产生一定影响;随着自重应力的逐渐增加,边坡体一定范围内的土体逐步进入塑性状态并产生一定的塑性变形。为考虑塑性应变在坡体局部累积过程中对最大主应力方向角α的影响,通过分级加载方式将各层土体的重力施加于模型。通过分级加载,实现边坡体不同区域二级分区的动态调整;与此同时,计算各二级分区各向异性强度参数并对其进行赋值。该加载共有3 级,各级荷载施加值如表3 所示。

表3 分级荷载施加值Table 3 Load application values for graded loads
为使土体强度的各向异性更切合实际,在分级荷载施加过程中采用了分区技术。分区采用初分、细分和精分3 级控制。1)初分,每级荷载施加完成后,计算所有土体单元角α的大小,并以0°~30°、30°~60°和60°~90°为划分标准,对I、Ⅱ、Ⅲ和Ⅳ 4 个大区进行初次区域划分。2)细分,初次区域划分后,由于同一区域内可能包含不同性质的土层,为保证后续划分结果的准确性,对包含不同性质土层的初次划分区域进行二次细分,即以土层界面为分界线,将该分区划分为与土层数相等的若干二级分区。3)精分,细分完成后,结合数值模拟结果并利用式(5)~式(9)各向异性强度参数计算公式,计算3 次分级加载下各区域内土体的c、φ值,与此同时,对细分后发生变化的区域即时进行调整。第1级加载时,取α=0°时对应的各土层强度参数。各级加载的分区演化如图3 所示,各参数的演变如图4所示。
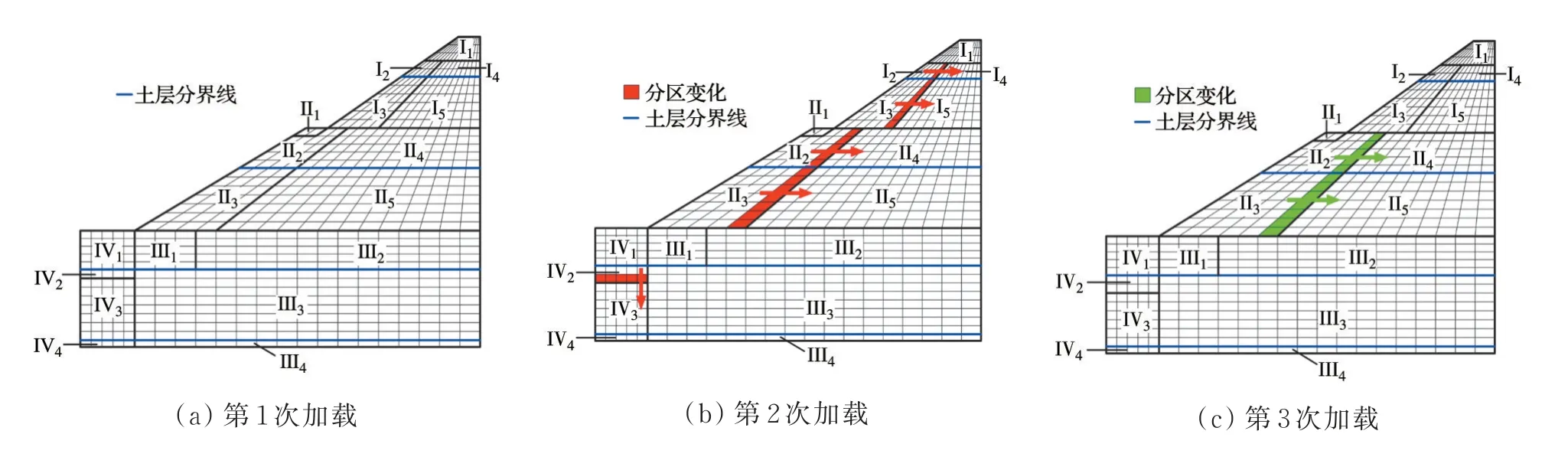
图3 各级加载的分区演化Fig.3 Partition evolution for each level of loading

图4 强度参数调整Fig.4 Strength parameter adjustment
图3 表明:在3 次荷载施加过程中,I、Ⅱ、Ⅲ和Ⅳ 4 个初始分区的二级分区数量没有增加或减少,但二级分区的分布域发生了一定变化,且分区演化范围逐渐减小;分区演化主要发生在α为30°~60°的范围内。第2 次加载后,I2、I3、Ⅱ2、Ⅱ3和Ⅳ2五个二级分区范围有所扩大,如图3(b);第3 次加载后,Ⅱ2和Ⅱ3范围进一步扩大,如图3(c)。从图4 可以看出,各分区α平均值和强度参数的变化范围随着荷载的逐级施加而逐渐减小。
3.3 基于流固耦合的边坡稳定性分析
建立考虑土体分区各向异性(工况1)、未分区各向异性(工况2)和未分区各向同性(工况3)3 种工况的流固耦合模型,模拟分析了边坡应力场、位移场和渗流场的变化规律。模拟所得各工况平均应力云图如图5 所示,塑性应变云图如图6 所示,流速 云图如图7 所示。

图5 平均应力云图Fig.5 Average stress cloud diagram

图6 塑性应变云图Fig.6 Plastic strain cloud diagram

图7 流速云图Fig.7 Flow velocity cloud diagram
由图5~图7 可知:工况1 的平均应力最大值较工况2 下降了6.4%,较工况3 上升了15.8%。工况1、2、3 的边坡滑动带宽依次增大,平均滑动带宽分别为2、3、5 m;3 种工况的坡体滑动深度、渗流域和流速大小[22-23]逐渐增大,其中,滑动深度分别为18.0、19.0、19.7 m。模拟过程中还发现:3 种工况的边坡塑性区贯通时间逐渐延长;工况1 在第10 个折减增量步时塑性区完全贯通,而工况2、3 分别在第18、第29 个折减增量步时塑性区才完全贯通,说明工况1的边坡滑动时间先于工况2、工况3。
为确定边坡的稳定性状态,以二级台阶坡肩顶点d点为追踪研究点(如图2 所示),分别以有限元计算结果是否收敛(标准A)、特征点位移出现拐点(标准B)和是否形成连续的贯通区(标准C)作为评价标准[4,24],计算所得3 种工况的边坡稳定性系数变化曲线如图8 所示(图中A、B和C为判断标准,1、2和3 表示工况)。
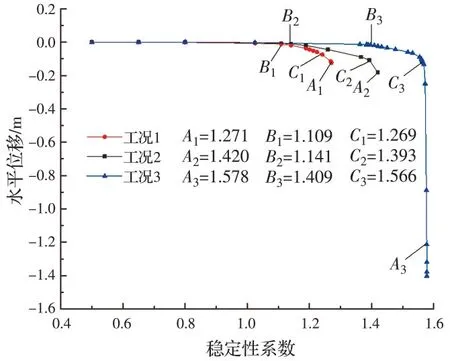
图8 稳定性系数变化曲线Fig.8 Stability coefficient variation curve
研究表明,标准A和标准B均可作为边坡失稳的判断依据,而标准C为边坡失稳的必要非充分条件[3];与其他两种标准相比,标准B与采用极限平衡法计算所得边坡稳定性系数的误差最小[14,24]。由图8 可以看出:以标准B为判断标准计算所得边坡的稳定性系数相对最小,3 种工况的边坡稳定性系数分别为1.109、1.141 和1.409;工况1 的稳定性系数相比于工况2、工况3 分别下降了2.8%和21.3%。
4 结论
1)方向角α的大小沿坡体外自由边界向坡体内部逐渐增大,且随着荷载的逐级施加,该变化过程逐渐趋于稳定。
2)考虑分区土体强度各向异性时,与其他两种工况相比,边坡体塑性区贯通时间最短,滑动带深度最浅,渗流域和流速最小。
3)采用3 种判断标准确定的边坡稳定性系数中,考虑分区土体强度各向异性时的边坡稳定性系数值最小,其次为未考虑分区土体强度各异性时,而未分区各向同性时的边坡稳定性系数值最大。
