波浪锥型风力俘能结构能量转换效率

2023-08-30闫豫龙柳迪伟郑云龙

上海交通大学学报 2023年8期

邹琳, 闫豫龙, 陶凡, 柳迪伟, 郑云龙

(武汉理工大学机电工程学院,武汉 430079)

传统的水平轴风力发电机存在结构复杂、安装维护困难、承受载荷混杂等缺点[1],通常放置在沿海、近海和其他高风速地区,低风速条件下风力发电机转速会发生骤降,导致功率输出与部件可靠性降低[2].Adel[3]提出了一款名为Vortex的无叶片风力发电机,利用结构周围空气形成的漩涡晃动柱体,继而将柱体振动机械能转化为电能.无叶片风力机基于涡激振动的原理,能在低风速环境下有效捕获漩涡能量,提高对风能的利用效率[4].虽然目前基于流致振动的俘能设备其风能转换效率仍弱于水平轴风力机,例如Hemon等[5]设计的风力俘能结构,风能转换效率不到1%;Badhurshah等[6]提出的双稳态弹簧的涡激振动俘能结构,最大转换效率为10%,但这类系统因其适应各种情况的潜力而仍然令人感兴趣.相较于水平轴风力发电机的高风速要求,无叶片风力发电机则可进行小型化设计并可用于低风速地区分布式风力发电布局,适合作为无线传感器网络系统的能源利用和区域小型电力系统[7].增强涡激振动有利于无叶片风力机采集风能并转换为电能,而质量比、阻尼比等控制参数对无叶片风力机俘能结构的涡激振动能量转换有重要影响.对此,国内外学者开展了诸多研究.

Zhang等[8]研究表明高阻尼比显著抑制圆柱俘能结构涡激振动能量转换效率.Kumar等[9]和李小超等[10]发现圆柱俘能结构出现最佳能量转换特性的折合流速与阻尼比有关.Zheng等[11]数值研究证明质量比会对涡激振动能量转换造成影响.Zhao等[12]、Xu等[13]和Wang等[14]均设计出改型圆柱结构的涡激振动俘能装置,其俘能功率和能量转换效率较圆柱俘能结构显著提升,并提出俘获能量与阻尼比呈正相关.分析上述文献可以看出,绕流结构的截面形状对涡激振动俘能装置的能量转换也起着不可忽视的作用.Lam等[15]给出合适的波长比、波幅比参数使波浪型圆柱具有明显的减阻效果.Chizfahm等[16]研究证明圆锥柱型无叶片风力俘能结构在高风速下具有良好的能量转换性能.邹琳等[17]在波浪圆柱中引入斜率得到一种波浪锥型圆柱,发现适合的波长比、波幅比、斜率组合可以增强柱体振动.

目前,涡激振动能量转换的研究大多集中在水生能源圆柱俘能结构,本文提出的波浪锥型风力俘能结构的能量转换特性尚无人研究.通过数值模拟分析质量比、阻尼比对波浪锥型俘能结构涡激振动特性、能量转换效率的影响.寻求合适的质量阻尼参数,以增大振幅、提高振动频率和拓宽锁频区间为目的,为波浪锥型风力俘能结构能量转换效率的提升提供理论支持.

1 数学模型

1.1 波浪锥型俘能结构-发电机-负载耦合模型

俘能结构模型示意图如图1所示.图1(a)为基于涡激振动的波浪锥型无叶片风力发电机物理模型,主要由4个部分组成:① 波浪锥型俘能结构;② 弹簧-阻尼系统;③ 传动机构,包括连杆、直线轴承、万向节联轴器等;④ 直线发电机.波浪锥型俘能结构-发电机-负载耦合模型可以简化为质量-弹簧-阻尼模型,如图1(b)所示.图中:Fflu为流体力;k为弹簧刚度;c,c0,cg分别为结构阻尼、发电机内能损耗阻尼、负载电阻发电阻尼;Fres为发电机对俘能结构的阻力;R0为发电机的内阻;RL为外界负荷电阻.对涡激振动而言,X方向的振幅往往远小于Y方向振幅,且单自由度运动更便于能量收集,故俘能系统仅被允许在Y方向做单自由度运动.风力作用迫使俘能结构发生Y方向涡激振动,振动机械能经传动机构传递至永磁发电机动子,进而动子切割磁力线产生电能.

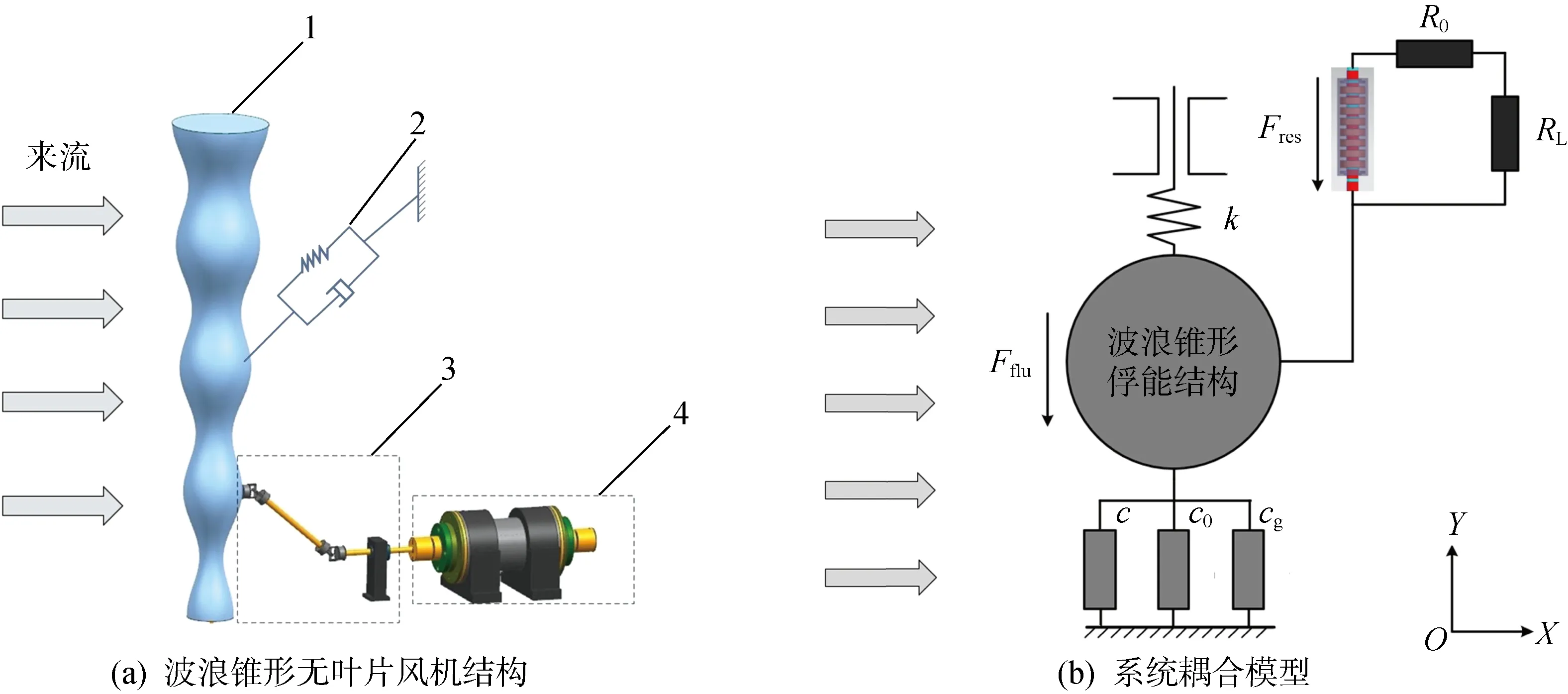
图1 俘能结构模型示意图Fig.1 Schematic diagram of energy harvesting structure model

耦合模型发生涡激振动时,俘能结构在Y方向受流体力Fflu和发电机阻力Fres,波浪锥型俘能结构的运动方程可由下式表示:

(1)

(2)

(3)

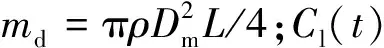
假设俘能结构位移y与发电机动子位移yg存在倍数关系,传递效率为α,则俘能结构与发电机动子之间存在关系:

(4)

(5)

俘能结构受到的发电机阻力为

(6)

将式(1)、(2)、(3)、(6)整理化简得耦合模型运动方程:

(7)

式中:mt为考虑流体附加质量的俘能结构总质量;ct为考虑发电机和传动机构后的俘能结构总阻尼;F(t)为流体对俘能结构作用力,也被称为升力.

1.2 能量转换效率

由于涡激振动具有周期性,俘能结构一个周期T范围内的平均有效功率如下式表示:

(8)

式中:T为涡激振动周期.于是,俘能结构从流体中获取的平均有效功率为

(9)

式中:fosc为俘能结构振动频率;A为俘能结构振幅;Cl为升力系数幅值;φ为相位角,即升力与波浪锥型俘能结构振动位移之间的相位差.

流体的动压为1/2ρv2,流体扫过波浪锥型俘能结构的面积简化为DmL,则施加在俘能结构上的力为1/2ρv2DmL.波浪锥型俘能结构的流体功率Pflu为流体作用力与来流速度的乘积:

(10)

故波浪锥柱俘能结构发生涡激振动时对流体能量的转换效率为

(11)

2 计算模型及验证

2.1 控制方程

将波浪锥型俘能结构的涡激振动视为非定常和不可压缩过程.研究发现,SSTk-ω湍流模型能很好地预测反向压力梯度流动,在总体预测能力方面似乎更好,结果更加真实[20].采用近壁面的k-ω模型和远壁面的k-ε模型,用黏度限制器构建湍流黏度μt是SSTk-ω模型的最大优势.因此采用雷诺平均Navier-Stokes (RANS)方程结合SSTk-ω湍流模型模拟俘能结构的涡激振动响应过程.

无量纲不可压缩RANS方程为

(12)

(13)

(14)

(15)

μt为湍流黏度[21],

(16)

2.2 俘能结构

波浪锥型俘能结构如图2所示,其中DH和DL分别为波浪锥柱对应斜率为k的直锥柱最大直径和最小直径,结构的几何特征表达式如下:

图2 波浪锥型结构示意图Fig.2 Schematic diagram of wave conical structure

Dz=Dm+2acos(2πz/λ)+k(z-L/2)

(17)

式中:Dz表示波浪锥柱对应高度Z处的直径;L=7Dm;a、λ分别表示波浪锥柱的波幅与波长.根据杨耀宗[22]的研究,选取振动性能最佳的一组参数,即k=0.05,a/Dm=0.1,λ/Dm=1.75.

2.3 计算模型

计算域大小为30Dm×20Dm×10Dm,笛卡尔坐标系原点位于圆柱中心,圆柱中心距入口10Dm, 距出口20Dm,x正方向为顺流向,y方向为涡激振动的方向,z正方向沿俘能结构中心向上,如图3所示.设置来流为空气,入口边界采用均匀速度入口(Velocity inlet),在雷诺数Re=3 900的条件下,入口速度为5.772 m/s;出口边界为压力出口(Pressure outlet),相对压力为0 MPa;上下面及侧面设置为对称边界(Symmetry);俘能结构表面设置为无滑移壁面(No slip wall).

2.4 可靠性验证

2.4.1计算策略验证采用瞬态CFD方法,为保证计算策略的准确性,需要对网格划分数量N和时间步长Δt进行无关性验证. 如图4所示,验证对比折合流速范围为Ur=4.8～13.2,质量比与阻尼比固定为m*=10,ζ=0.01下的波浪锥形俘能结构的振幅比.图4(a)对3种网格密度(904 337/1 382 078/1 499 493)进行了网格敏感性研究,图4(b)则对3个时间步长(0.001/0.000 5/0.000 25)进行了时间步长独立性验证.从图中可以看出,网格数量达到 1 382 078 后振幅几乎不再变化,而时间步长设定Δt=0.000 5 时柱体振幅已和Δt=0.000 25 时近似相同.进一步地,以升力系数、阻力系数和振幅作为对比因素,选取Ur=7.2时波浪锥型俘能结构进行涡激振动数值模拟的验证结果,如表1所示.可以认定Case4网格密度N=1 380 278、无量纲时间步长Δt=0.000 5 的计算精度与速度正确合理,平均阻力系数Cd,m、脉动升力系数Cl,r均已近似不再变化,最大振幅Amax与文献[17]中相差不到0.3%,可用于波浪锥型俘能结构仿真实验.

表1 无关性验证结果对比Tab.1 Comparison of verification results

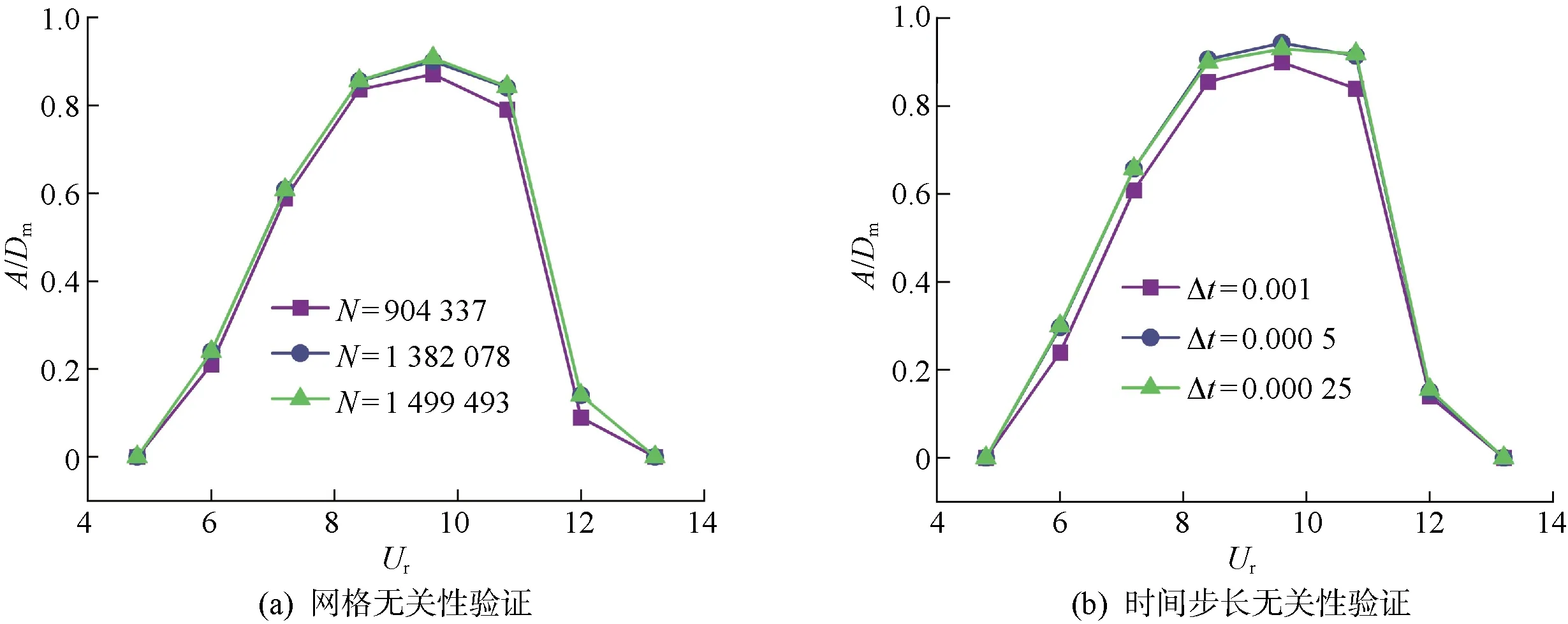
图4 计算策略无关性验证Fig.4 Calculation strategy independence verification

2.4.2实验验证涡激振动实验布置如图5(a)所示,试验段4个侧面采用可拆卸亚克力挡板,实验模型上下两端开孔方便炭纤维杆支撑固定并连接到尼龙线.波浪锥型俘能结构如图5(b)所示,采用8200Pro材料3D打印制作.位移测量原理如图 5(c)所示, 图中U∞为风洞来流. 风洞来流绕过实验模型在其后方产生涡脱,涡脱频率接近俘能结构-尼龙线-弹簧系统固有频率时发生共振,通过试验台下方激光位移器发射和回收激光,由采集设备输出涡激振动位移时程曲线.整体测位移装置包括示波器、电源、控制器和激光头.

图5 涡激振动实验装置Fig.5 Vortex-induced vibration experimental device

振幅比验证对比如图6所示.图中:Num表示数值仿真;Exp表示实验测试.由图可见,质量比m*=10,阻尼比ζ=0.01时仿真结果与文献[22]中结果非常吻合,锁频区间和振幅比基本一致.因为风洞实验箱和俘能结构模型尺寸并不完全匹配,所以采用等比例设计放大俘能结构,其质量比达到m*=46.2,在与其相同的质量比、阻尼比参数下进行仿真对比,发现锁频区间与振幅比近似相同,曲线变化趋势较接近,因此认定本文的计算策略和用户自定义函数(UDF)程序正确可靠.

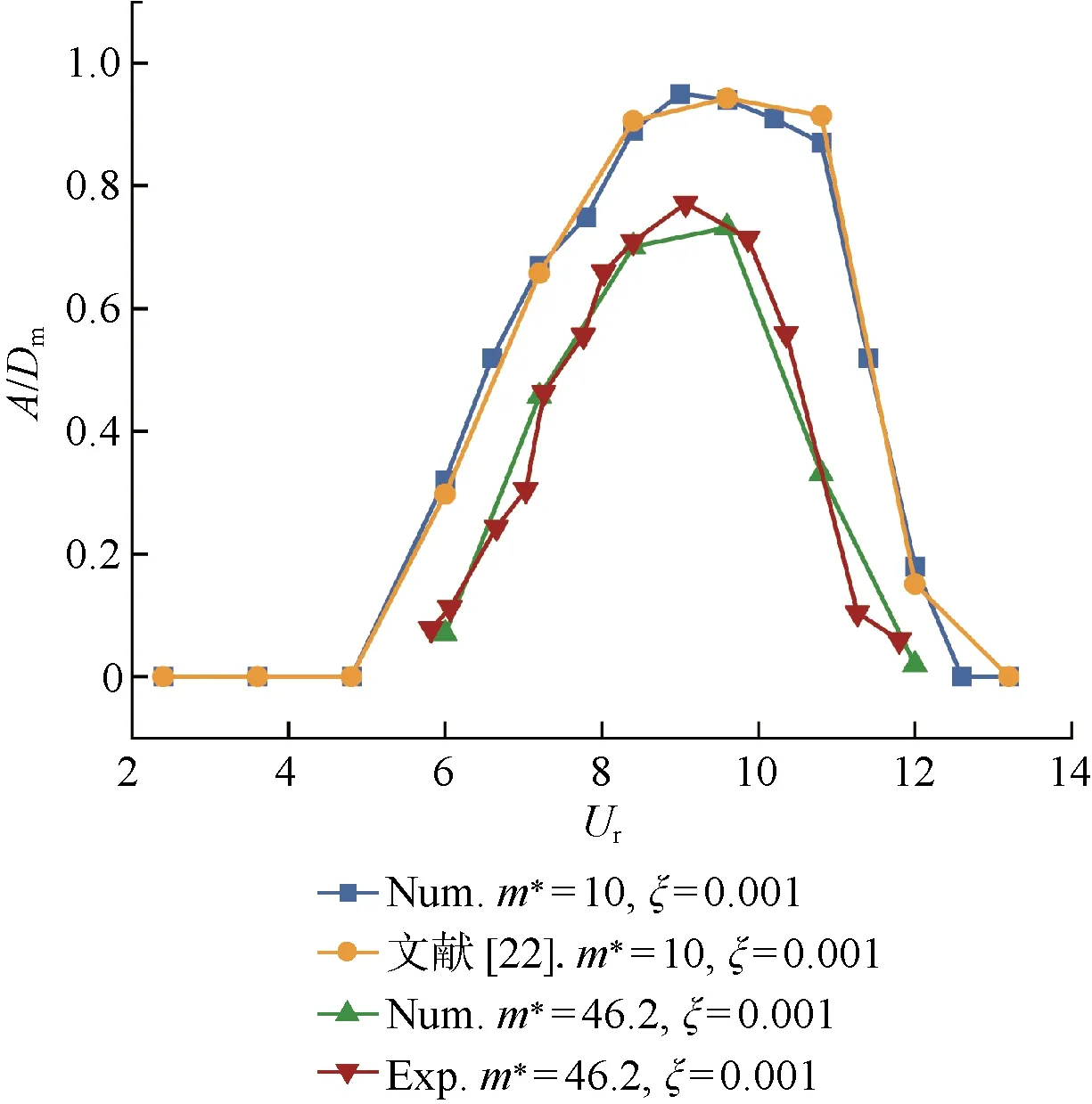
图6 振幅比验证对比Fig.6 Comparison of amplitude ratio verification

3 结果分析

3.1 方案设计

由上文可知,基于涡激振动的小型风能采集器可以在相对较低的风速下产生运动,可以从各种地区频繁和广泛的风速中俘获能量,如Vortex无叶片风力发电机在风速区间为1～9 m/s的地区进行模型试验.本文设计的波浪锥型俘能结构希望应用于城市环境下的小型区域分布式无叶片风力发电机发电系统,而城市环境风速一般在1～7 m/s范围内[23],因此确定Re=3 900 也即风速v=5.772 m/s条件下进行仿真模拟,从而切合城市环境常见风速条件.因此,探究合适的波浪锥型俘能结构质量比、阻尼比组合,有效地将低速环境风的动能转换为电能至关重要.表2为质量比、阻尼比组合的实验方案设计,探讨质量阻尼参数对波浪锥型俘能结构涡激振动响应及能量转换的影响规律.

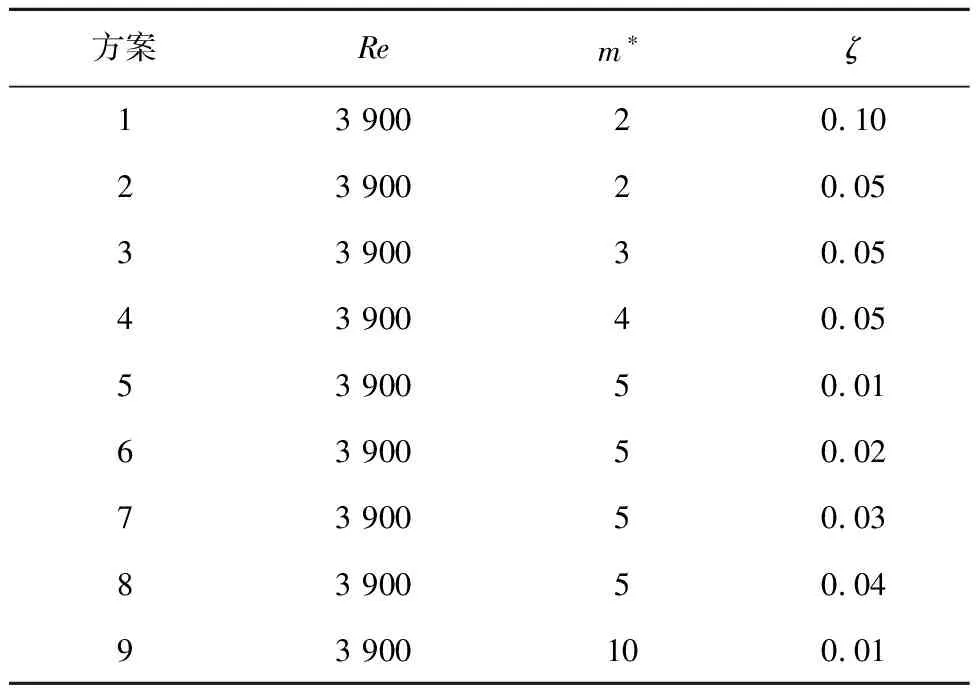
表2 实验方案设计Tab.2 Experimental design

3.2 m*和ζ对振幅比、频率比的影响

对振幅A、振动频率fosc进行无量纲化处理:A*=A/Dm,f*=fosc/fn.其中fn为结构固有频率,A*和f*为振幅比、频率比.A*和f*直接影响波浪锥型俘能结构捕获能量的大小.

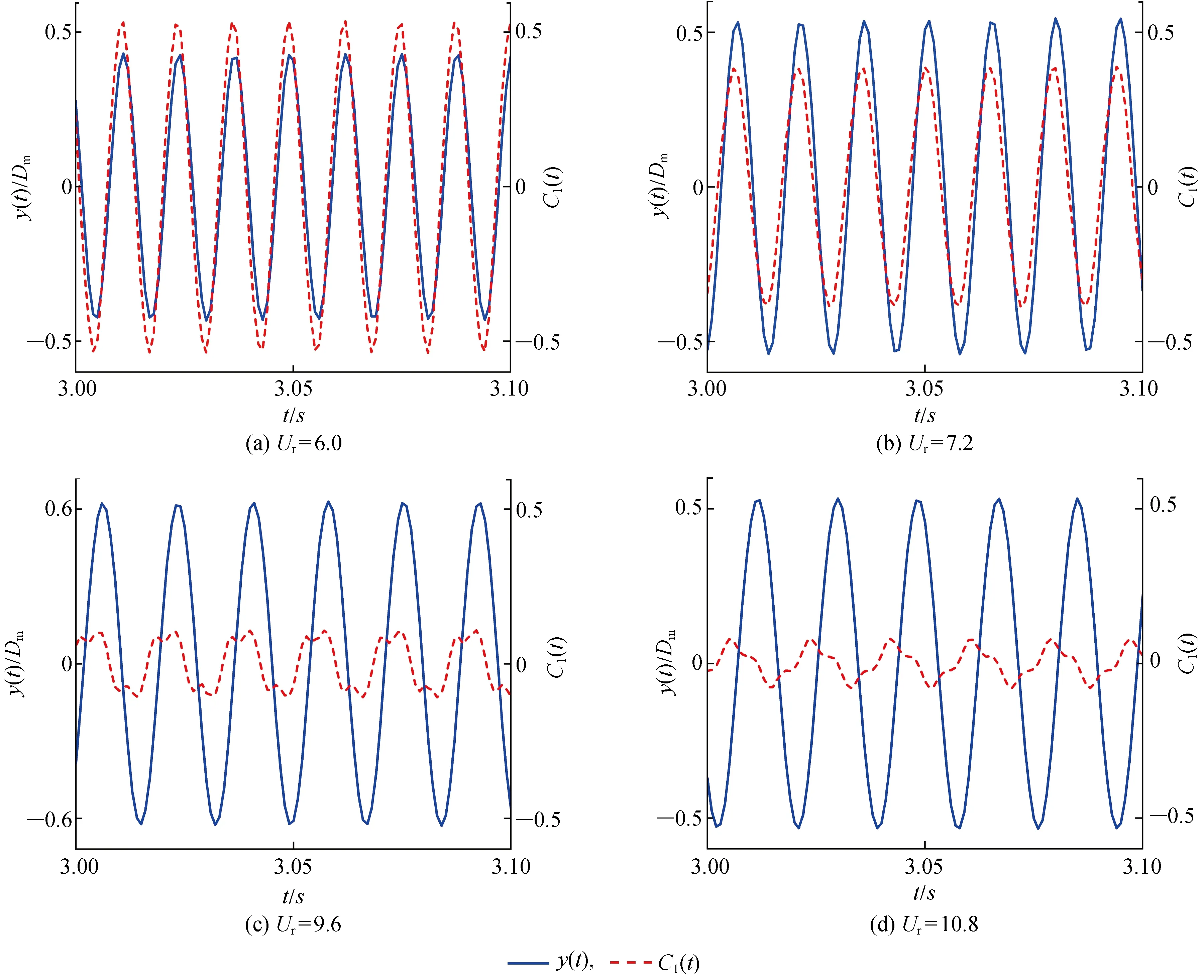
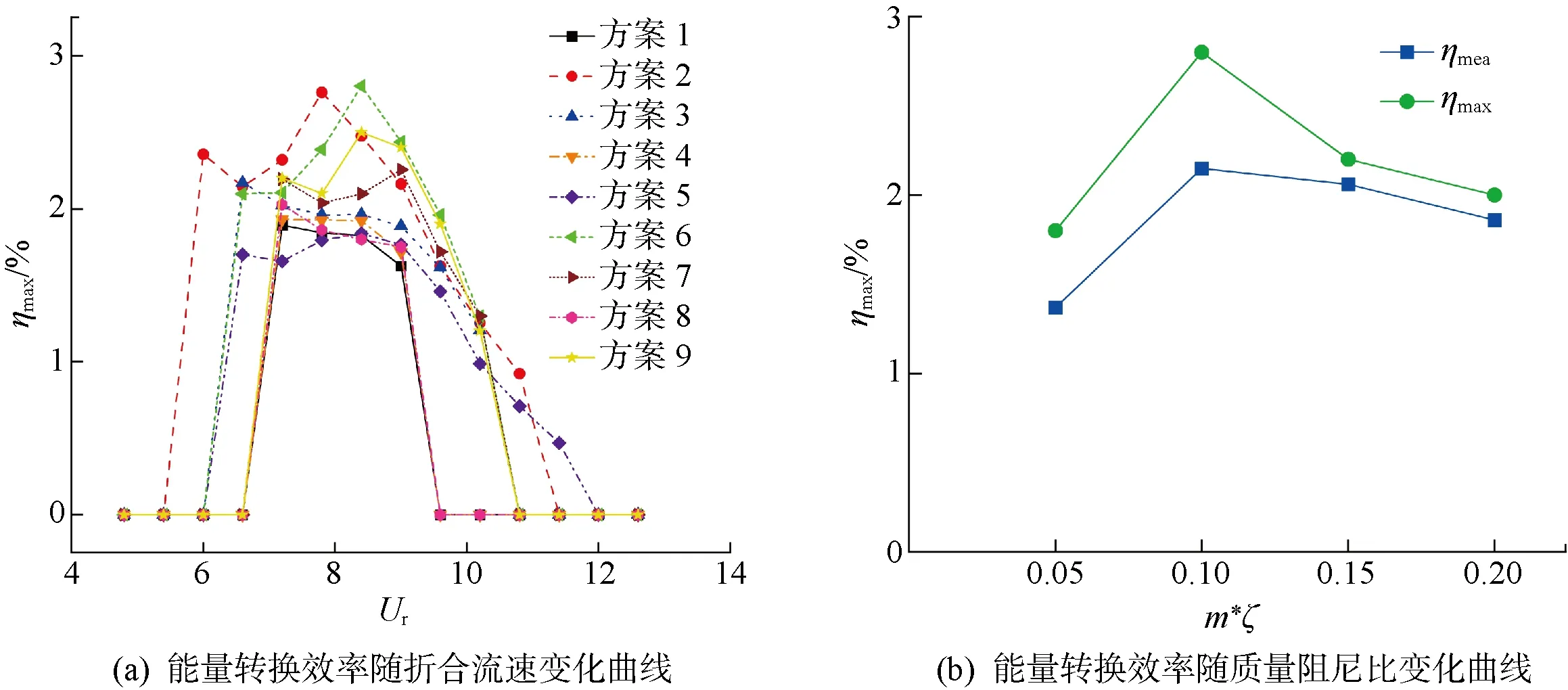
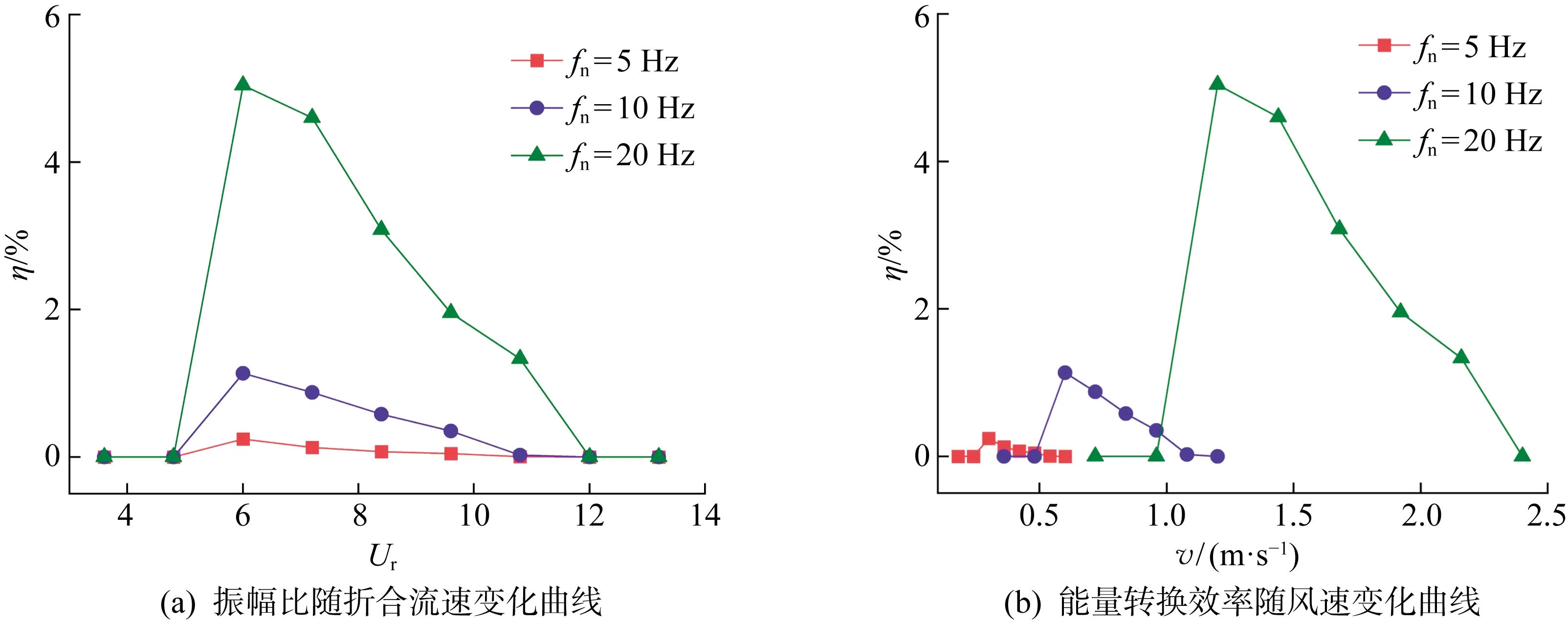
图7(a)为波浪锥型俘能结构振动响应振幅比A*随折合流速Ur的变化曲线.可以看出质量比和阻尼比对波浪锥型俘能结构锁频区间有显著影响.当阻尼比ζ=0.05不变的情况下,锁频折合流速区间会随着质量比的增加而缩短.阻尼比对锁频区间也有着相似的影响,由m*=5的4组方案可以看出,随着阻尼比的增加锁频区间减小.m*=5,ζ=0.01的锁频区间最广,在6.6

图7 无量纲振幅比、频率比曲线Fig.7 Dimensionless amplitude ratio and frequency ratio curves

图7(b)给出了频率比f*随折合流速的变化曲线.Ur<6.0时,频率比趋于0,此时俘能结构未进入锁频区间,当m*=2,ζ=0.05,Ur=6.0时,频率比变化到0.821,随后频率比随着折合流速增加而逐渐增加,当Ur=10.8时,f*增加到1.029,波浪锥型俘结构的振动频率大于固有频率,但此时振动幅值已经较小即将退出锁频区间.其他质量比、阻尼比条件下频率比f*的变化规律类似,进入锁频区间时,频率比迅速从0上升至趋于1附近,随后在整个锁频区间,频率比f*都随折合流速的增加而增加并在退出锁频区间前达到最大,随后退出锁频区间f*降到0附近.

可以看出质量比m*对频率影响比f*的影响大,以ζ=0.05为例,同一折合流速下,较大的质量比对应的频率比也越大.而阻尼比ζ对频率比的影响较小,当m*=5不变而ζ改变时,进入锁频区间后各折合流速下的f*基本重合.

3.3 m*和ζ对升力系数幅值、相位角的影响

过往的研究中发现,除了振幅和频率之外,发生涡激振动时的升力系数幅值Cl和相位角正弦值sinφ同样会影响流体和俘能结构之间的能量传递.图8(a)、8(b)分别为升力系数幅值Cl、相位角正弦值sinφ随折合流速的变化曲线.

图8 升力系数幅值、相位角变化曲线Fig.8 Lift coefficient amplitude and phase angle change curves

从图8(a)可以看出,当Ur=6.0时,m*=2,ζ=0.05的俘能结构升力系数幅值Cl迅速从0增加到0.537,随后随着折合流速的增加而逐渐减小,当Ur=10.8时,Cl降低到0.08,直至退出锁频区间减小到0.其他质量比、阻尼比条件下也有类似规律,升力系数幅值在进入锁频区间之后迅速达到最大值,随后随着折合流速的增加而逐渐减小,直至退出锁频区间趋于0.同时可以发现质量比、阻尼比对Cl也有较大影响,质量比、阻尼比越大,同一折合流速下对应的升力系数幅值越小.同一质量比、阻尼比条件下升力系数幅值对应的折合流速与振动幅值对应折合流速并不重合,说明升力越大并不意味着升力对涡激振动的作用越大.

学者们认为相位角φ在0°～180°范围内时流体可将能量传递给俘能结构,结构发生周期性运动;而当相位角在 -180°～0°范围内时,能量从俘能结构传输给流体,此时结构不会发生振动.从图8(b)中可以看出,在锁频区间内sinφ均为正值,相位角在0°～180°之内,此时波浪锥型俘能结构发生涡激振动,俘能结构可以从流体中俘获能量.未进入锁频区间前,相位角均在0°附近,刚进入锁频区间sinφ较小,之后sinφ随着折合流速的增加而逐渐增加,在退出锁频区间之前达到最大值,直至退出锁频区间后,sinφ又降到0附近.质量比和阻尼比对sinφ也存在着影响,随着质量比或者阻尼比的增加,在同一折合流速下,对应的sinφ先增加后减小,这也说明质量比和阻尼比对能量转换的影响并不是单纯的越大越好或者越小越好,存在一组合适的质量比、阻尼比组合使振动响应更好.

Cl和sinφ可以表征升力的大小和升力对振动响应的作用,升力系数幅值和相位角正弦值的乘积Clsinφ越大,表示波浪锥型俘能结构与来流的相互作用越强,如图9所示.从图中可以看出在进入锁频区间后,Clsinφ迅速达到最大值,随后随着折合流速增加而逐渐减小.当质量比不变时,阻尼比越大,俘能结构与流体间的相互作用也越大,在阻尼比不变的情况下,改变质量比也有类似的规律.质量比、阻尼比对能量转换的影响是非线性的,Clsinφ随着质量比、阻尼比增加而变大,但同时振幅与锁频区间也会减小.

图9 Clsin φ随折合流速变化曲线Fig.9 Clsin φ versus reduced velocity

为了更好地展示相位角对振动的影响,以m*=2,ζ=0.05的升力系数幅值与振动位移时程图为例,如图10所示.折合流速Ur=6.0,7.2时,波浪锥型俘能结构的升力系数和位移呈现“同相位”特征,此时φ值较小;当Ur=9.6时,升力系数与位移除呈现出“同相位”特征之外,升力系数还呈现出“拍”的特征;当Ur=10.8时,升力系数与位移交替出现“同相位”与“反相位”特征.结合图8,Ur=6.0,7.2时sinφ较小,位移与升力系数相位差较小,表现为时程图“同相位”,而当Ur=9.6,10.8时相位差较大,时程图出现“拍”的特征和正反相位交替出现的现象.

图10 m*=2,ζ=0.05的升力系数幅值与振动位移时程图Fig.10 Time chart of Cl and vibration displacement at m*=2 and ζ=0.05

3.4 质量阻尼参数对能量转换效率的影响

根据式(11)推导可以计算出各折合流速下的能量转换效率η,不同质量比m*、阻尼比ζ、质量阻尼比m*ζ下能量转换效率变化曲线如图11所示.图11(a)中同一折合流速下的能量转换效率随阻尼比的增加先增大后减小,最大能量转换效率对应的折合流速并不与最大振幅相同.以ζ=0.05,m*=2,3,4为例,m*=2条件下Clsinφ未达到最大值,但此时振幅较大,能量转换效率最高.说明能量转换是各项参数综合作用的结果.同时可以发现质量阻尼比m*ζ相同的情况下,其能量转换效率曲线也十分接近.随着阻尼比的增加,锁频区间内无量纲振幅值和能量转换效率的增加趋势变缓.可以看出Ur=7.8时m*=2,ζ=0.05的最大能量转换效率略低于Ur=8.4时m*=4,ζ=0.05的转换效率,但m*=2,ζ=0.05条件下锁频区间更广,在整个折合流速范围内俘能效率最高,当Ur=7.8时风能转换效率达到2.8%.因此认为m*=2,ζ=0.05时,波浪锥形俘能结构的能量转换效率最高.

图11 能量转换效率曲线Fig.11 Energy conversion efficiency curves

本次实验使用的质量阻尼比m*ζ=0.05,0.10,0.15,0.20,计算出每个m*ζ下的最大能量转换效率ηmax及平均能量转换效率ηmea,整理出如图11(b)所示的曲线.可以看出质量阻尼比m*ζ影响着能量转换效率,而且存在着最优的m*ζ组合使得能量转换效率最高.m*ζ=0.10的情况下能量转换效率最高,平均能量转换效率较m*ζ=0.05提高了近31%.当应用涡激振动发电时,引入发电机会造成阻尼比较大的结果,这也提供一种思路:如果想要提高能量转换效率,可以在m*ζ一定的情况下,将俘能结构轻量化的同时提高发电阻尼在系统总阻尼中的比例.

3.5 fn对能量转换效率的影响规律

以质量比、阻尼比组合m*=2,ζ=0.05为对象,研究固有频率fn对波浪锥型俘能结构能量转换的影响,图12给出了固有频率fn=5,10,20 Hz下振幅比随折合流速、风速的变化曲线.从图12(a)中可以看出,改变固有频率不影响俘能结构发生涡激振动的锁频区间,同一折合流速下俘能结构的振幅随固有频率的增加而变大.

图12 固有频率对振幅比的影响Fig.12 Influence of natural frequency on amplitude ratio

本文的波浪锥型俘能结构能量转换效率研究限定在Re=3 900情况下,风速v固定为5.772 m/s.而在实际应用中来流速度会不断变化,因此有必要研究实际风速下的能量转换规律.根据Ur=v/(fnDm)可以得出不同固有频率下折合流速Ur对应的实际风速,图12(b)为振幅比随风速的变化曲线.从图中可以看出,固有频率增加不但可以提高振幅,同时又可以拓宽涡激振动锁频区间,波浪锥型风力俘能结构可以在更大的风速范围内俘获能量.

固有频率对能量转换效率的影响如图13所示.从图13(a)中可以看出,能量转换效率η在进入锁频区间之后迅速达到峰值,随后η随着Ur的增加逐渐降低,在Ur不变的条件下,固有频率越大能量转换效率越高.在质量比阻尼比组合为m*=2,ζ=0.05,固有频率fn=20 Hz条件下,波浪锥型俘能结构的风能转换效率达到5.1%,并且风能转换效率会随着固有频率的提高而继续增大.从图13(b)中可以看出,fn的增加也会使得波浪锥型俘能结构俘能的实际风速范围增加.综上所述,在运用涡激振动进行风力发电时,适当的提高波浪锥型风力俘能结构固有频率可以提高能量转换效率,拓宽俘能风速范围,有效提升其能量转换特性.