基于多智能体的被装精准申领库存策略仿真研究*
2023-08-30史博元郑丽莎文昊林
史博元 董 鹏 郑丽莎 文昊林
(海军工程大学 武汉 430000)
1 引言
2018 年8 月,我军在全军72 个单位进行“精准申领”试点工作,经过两年时间的探索与改进,2021年,军委后勤部与多家地方物流公司签订战略合作协议,以战区为保障单位建立军民融合仓库,利用地方物流公司成熟的技术与经验,加速被装运输链路的“最后一公里”,同年4 月21 日,在全军范围内正式推广被装的“精准申领”保障模式[1]。不同的是,试点期间每年两次的“定期申领”升级成了“随时申领”:官兵可以在任意时间登录平台申领被装,并且可以实现十天内送达,极大地提高了被装保障效率。
在我军以往的被装实物供应模式中,长期存在着差异化需求难以满足、保障精确性不高、闲置浪费等问题,而被装精确申领模式很大程度上解决了上述问题,迈出了保障能力提升的关键一步[2]。但由于这种供应保障模式推行的时间较短,目前仍处于探索阶段,在供应链效费比方面还存在一定的不足,例如各节点库存控制策略不够精准,导致部分被装库存长期缺货或积压。本文在现有的库存控制策略基础上,利用anylogic仿真,对其存在的问题进行改进,以期实现提高效率、降低成本、减少浪费的目标。
2 策略分析
2.1 现状分析
目前,被装精确申领的供应链主要分为四个节点,分别是军需物资供应商(下称工厂)、军需物资仓库(下称军需仓库),配送服务供应商(下称物流公司)和部队用户,供应链中最常见的保障模式如图1 所示。首先,由军委后勤保障部定期汇总申领平台中的官兵需求信息,将其与军需仓库和工厂的库存进行汇总对接后,调配物资并开展下一个周期的采购,工厂根据订单,将被装送达军需仓库;而后,仓库将调配完毕的被装,送至军民融合仓库;最后由物流公司进行相应的分拣后,配送至部队用户[3]。这种库存控制策略对每个周期采购量预测的准确性依赖较大,但由于精准申领模式运行时间较短,可参考数据较少,加之新冠疫情的影响,难免会出现需求和产能两方面的波动,造成某些被装长期缺货,影响保障效率和质量,或者库存严重积压,浪费大量的库存成本。考虑到配送阶段由地方物流中心负责,本文只研究工厂和军需仓库的库存策略,着重从军方层面入手,降低成本、提高效率。
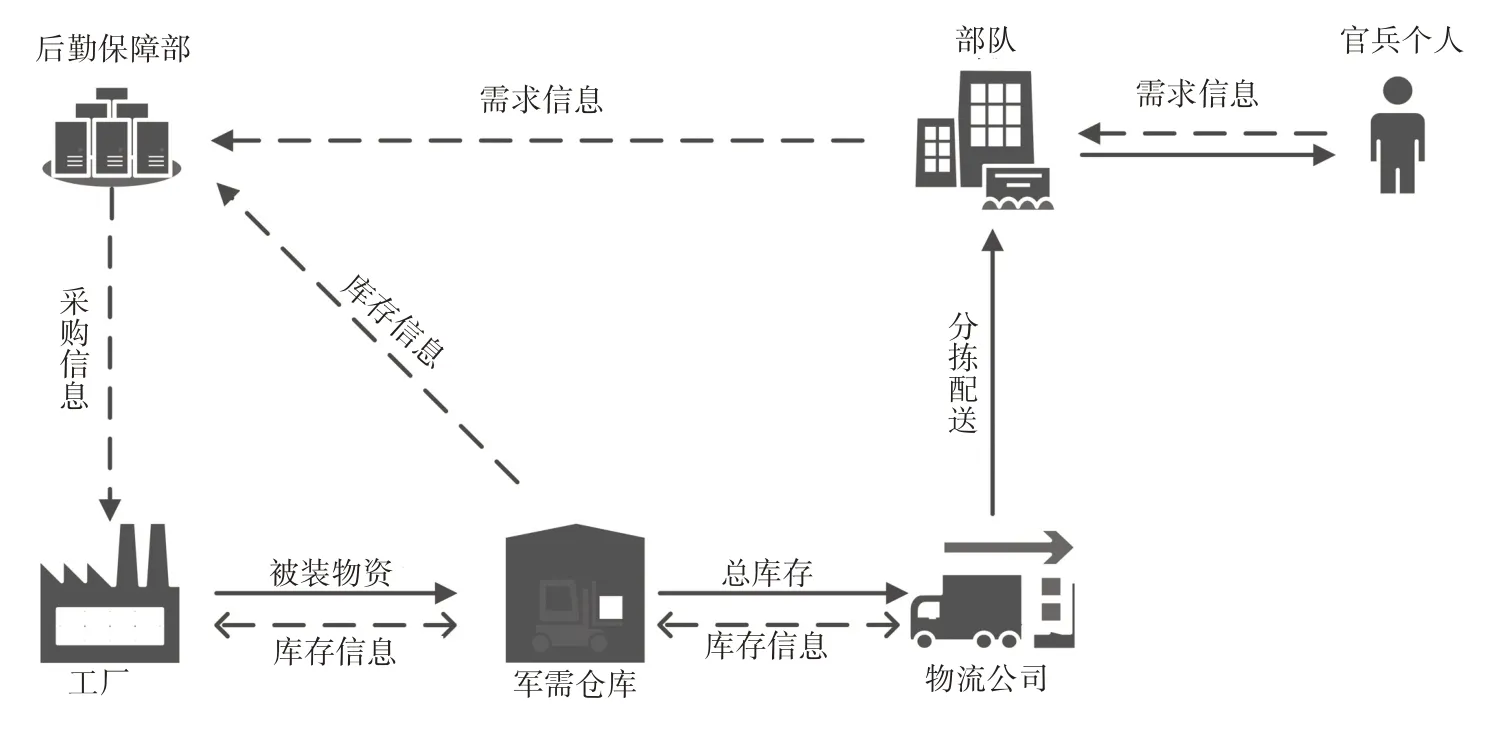
图1 常见供应链保障模式
2.2 军需仓库库存策略设计
本文采用的原始数据,来源于实行精准申领一年内中部战区Z 仓库某被装的库存量和需求量,去除起始阶段订单量暴增导致的极端数据,最终选取的时间范围为2021年5月7日至2022年4月21日,库存状态折线图如图2所示。
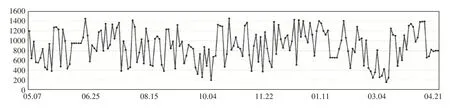
图2 库存状态折线图
数据显示,库存波动范围较大且水平整体偏高,产生大量的库存成本。针对库存策略的不足,进行改进并利用anylogic软件进行建模仿真。军需仓库库存状态图设计如图3所示。
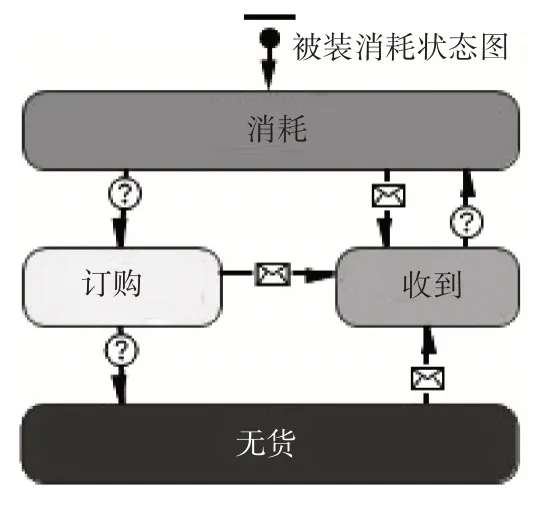
图3 军需仓库库存状态设计图
其库存策略及参数设计如下[5]:
1)库存阈值S:当军需仓库某型被装库存低于该数值时会向工厂订购产品。
2)订购批量P:每次向工厂订购的批量。
4)工厂要求的最小订购批量M。
由于每次订购产生的额外成本较低,可以忽略不计,因此根据经典EOQ 理论,通过降低订购批量可以达到降低成本的目的[4];另外,在可预见的未来,国内新冠疫情形势仍不容乐观,原料断供和工厂停产依旧会是常态,无疑将对生产和库存造成巨大影响。综合各种影响因素,应该尽量减少单次的采购批量,增加采购次数,降低成本的同时,将不确定性事件的影响降至最低[6],但是采购量还需要满足下列约束条件:
1)在采购期内满足最大需求。该最大需求可作为发起采购的时机,即库存阈值S。
2)满足下一个订购期的需求。若订购批量较小,在货物运输到仓库时库存可能无法满足需求,因此考虑最极端的情况,即每日都消耗最高的数量,即可推算出订购批量P。
3)采购量过低会急剧提高单位制造成本,所以采购批量要满足工厂的最小订购批量。
通过模拟仿真,得到的直接数据有:
1)fx:在x天内产品需求统计数据集,x为整数,max(fx)表示在x天内最大的需求量。
2)Fx:在x天内产品需求积累情况,x为整数。
对此,根据仿真系统计算出的多日需求统计数据,设计了以下几种库存策略。
若只考虑T 日内的需求情况,易得库存阈值S应为max(f),这样的库存阈值能够保证库存在天的时间内不会耗尽。考虑每个周期的需求量最大都为max()时为极限情况,天后的库存又会小于库存阈值,同时会发起第二次订货请求,此时订购批量P应为
通过仿真系统将参数带入,得到军需仓库库存变化情况,如图4所示。
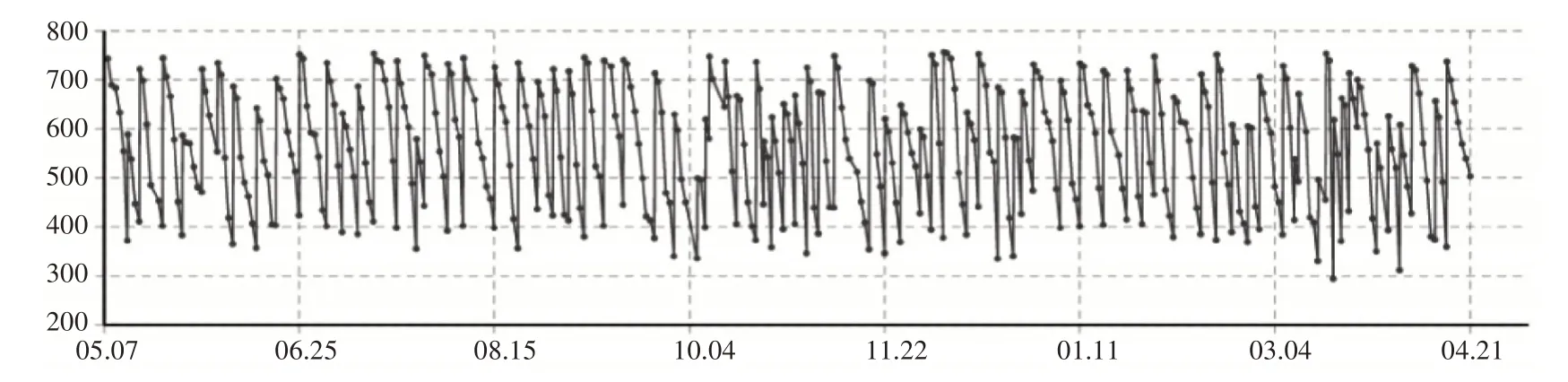
图4 军需仓库库存变化情况
分析图中数据可以得出,该库存策略虽然满足了全部需求,但整体库存仍维持较高水平,不够合理,这是由于现实中很少出现相邻几天需求都达到最大的情况,因此,还需对该策略进行进一步的优化。
在上述订购批量P 的条件下,可能会导致缺货,所以还需对订购批量进行修正:
通过仿真系统将参数带入,得到军需仓库库存变化情况,如图5所示。
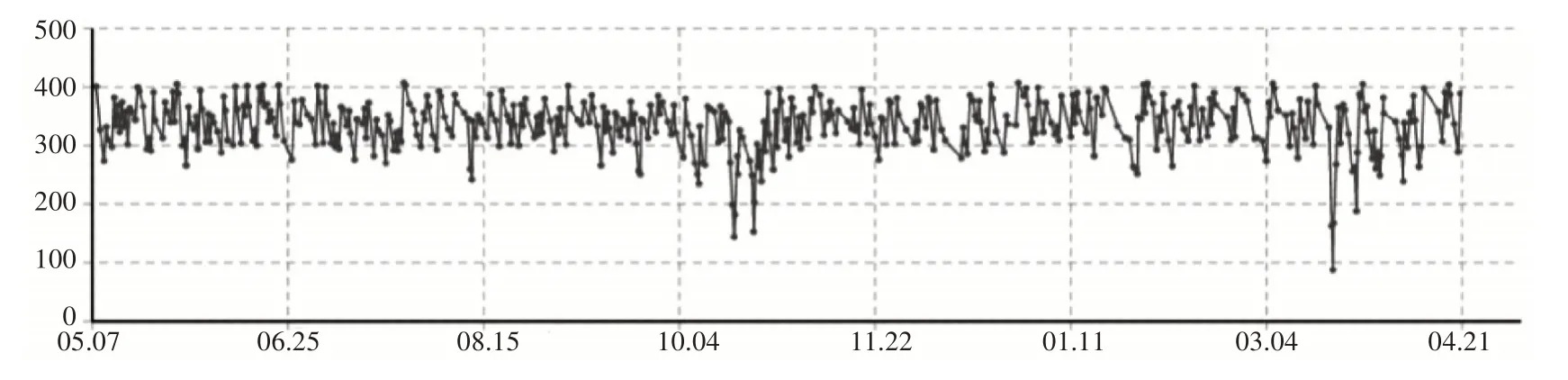
图5 军需仓库库存变化情况
图中最低库存水平没有趋近0,这是由于同时满足库存数量最低,且刚好遇到最大需求的概率较低,因此该方案比较符合实际情况。但方案也存在一些问题,考虑到部分被装的季节性特点,大部分情况下库存水平维持较高,只有一些特定月份需求较大,因此还可以通过考虑特殊时期进一步对库存方案进行设计[7],具体见2.2.3节。
2.2.3 按月规划库存策略
在前两种设计方案的基础上,设计按月规划库存的策略,原因在于考虑到了被装的季节性特点,目的是为解决因季节需求差异而导致的总体库存偏高的问题。以某型被装为例,通过分析该被装的适用季节及往年数据,发现在3 月及10 月,订单需求会有较大的增加。因此,只需使用2日需求分析的方法将每月的库存策略区分处理即可。对库存策略按月区分规划,得到库存变化如图6 所示,仓库根据历史需求信息和季节变化调整库存策略,从而能够达到降低库存成本的目的[8]。
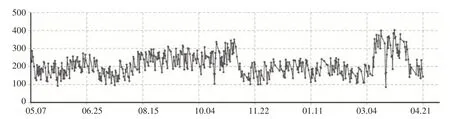
图6 军需仓库库存变化情况
2.3 工厂库存及生产策略设计
相比军需仓库,工厂的库存数量与被装产量有直接关系,因此还需要同步设计其生产策略。工厂的库存状态图设计如图7所示。
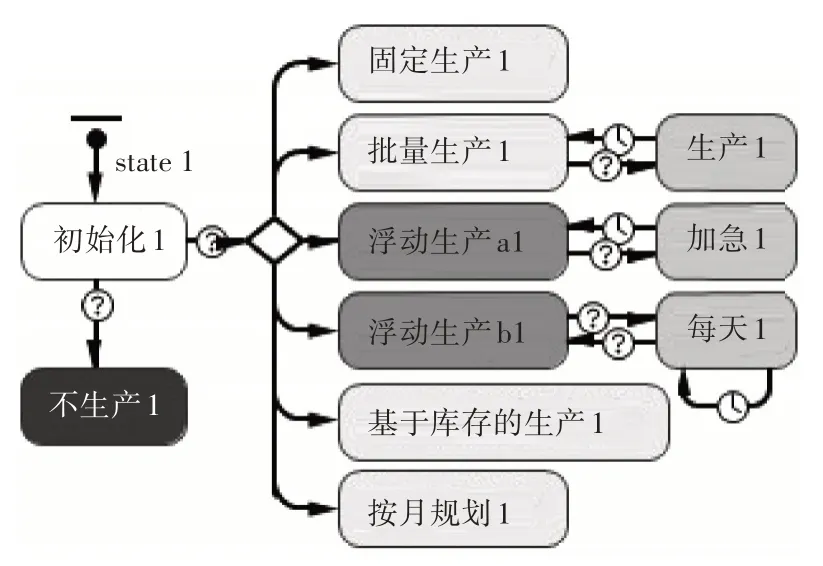
图7 工厂库存状态设计图
其库存及生产策略参数设计如下[9]:
1)每日生产R:每天生产固定数量的产品。
2)库存阈值S:当产品库存低于该数值时会进行加急生产。
3)生产批量P:加急生产的批量。
4)生产周期T:被装从生产、入库到最后出库的时间,单位为天。
通过模拟仿真,得到的直接数据如下:
1)fx:x天内产品需求统计数据集,x为整数,max(fx)表示在x天内最大的需求量。
2)Fx:从第1 天到第x天产品需求积累的情况,x为整数。
根据仿真系统计算出的多日需求统计数据,设计了以下几种生产策略。
2.3.1 固定生产策略
在该策略下工厂每天只生产固定数量的产品R,不进行加急生产,使得全年都可满足需求。所以为维持每年的总体需求,每日产量R 为,得出工厂库存变化曲线如图8所示。

图8 工厂库存变化情况
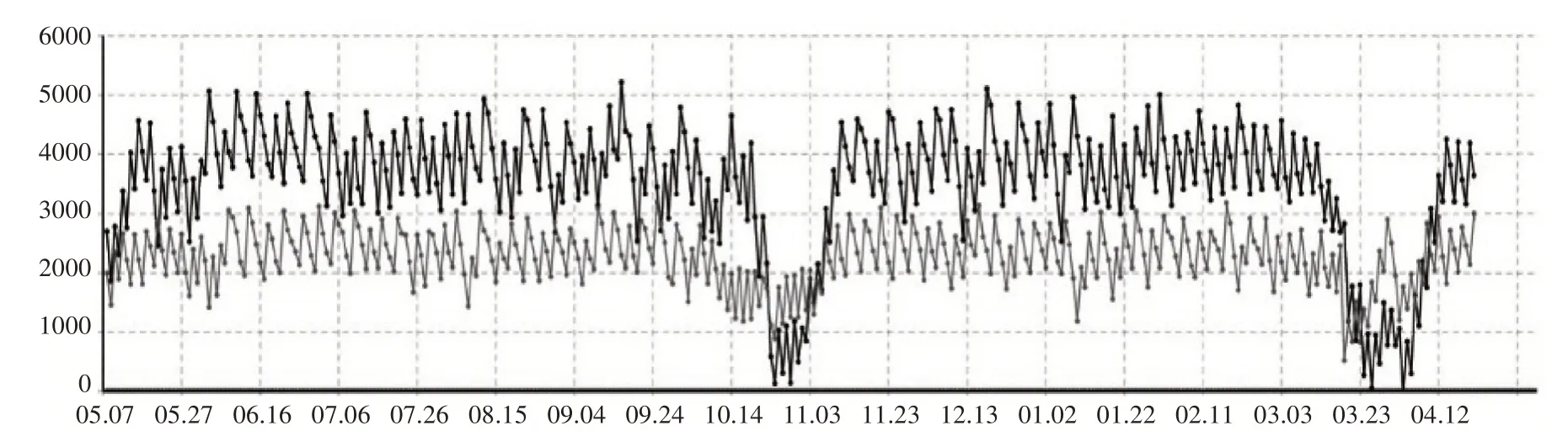
图9 工厂库存变化情况
由图8 可以看出,由于设定了较高的每日生产数量,库存水平会有一段时间的积压,维持在较高水平,且该策略需要比较合适的初始库存,不太符合实际情况。
2.3.2 批量生产策略
该策略类似于军需仓库库存策略的设计,在该策略中,每日固定生产量为0,当库存低于某一阈值时才开始生产。特点是工厂在低库存时生产固定的量后停工,但这种策略需要高库存水平以应对风险,且每日生产波动较大。
将参数带入仿真系统,得到工厂库存变化情况示意图如下所示:
2.3.3 二级生产策略
为了使每天生产数量波动变小,同时避免较高的库存水平,应结合2.3.1 节与2.3.2 节中的方案设计新的策略:工厂每天生产固定数量R 的产品,当库存低于某一阈值S 时,每天加急生产P 件产品,在生产时间T 天后交付。在这种生产策略下,生产批量分为两级:高库存时每天生产R 件产品,低库存时每天生产R+P 件产品。通过每日的固定生产满足部分需求,同时降低了高需求时的波动水平[10]。这种策略中的加急生产数量相对于前一种策略更少,生产波动更平缓,但会造成高水平库存的延迟,且生产时间越长,延迟增长越高。采用OptQuest Engine 智能优化引擎,进行500 次迭代,得到的库存变化曲线如图10所示。
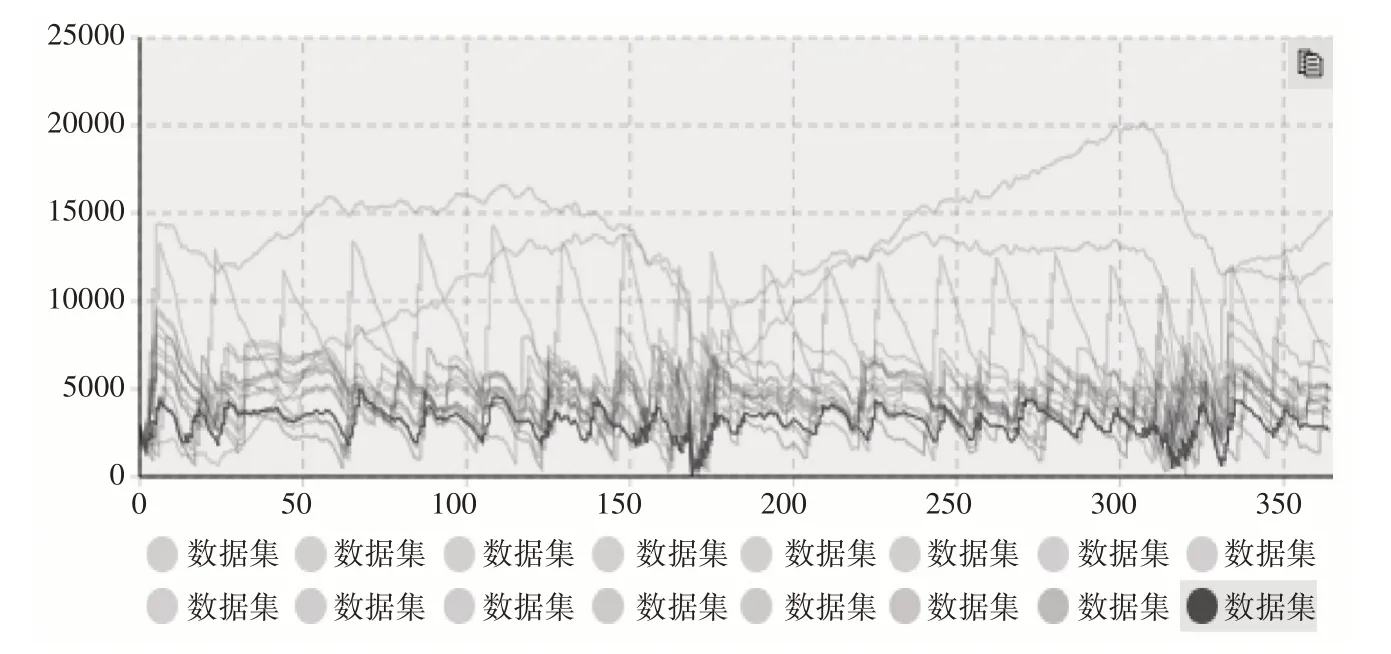
图10 库存变化情况
对比2.3.2 节中的数据,显然2.3.3 节中的策略生产数量的波动更小,且库存水平较低。对这种二级生产策略进行扩展,可以得到基于库存数量的生产策略,具体见2.3.4节。
2.3.4 基于库存数量的生产策略
在该策略下,输入数据为每日产品的需求量和生产时间,输出策略为生产数量关于产品需求量的表函数,也可以称之为多级库存控制策略,总体方法是将产品需求分布转换成生产数量与库存数量的关系[11]。设生产时间为T,每日产品需求量分布为f1。该策略的目标是使最低库存不下降到0 以下,且平均库存数量最低。在此策略下需要设计若干个控制点,其中横坐标为库存数量,纵坐标为该库存数量下应生产的产品数量,由此可以构建一个表函数,再使用插值计算[1],形成图像,将2.3.3节中的二级生产策略用这种方式表示如图11所示。
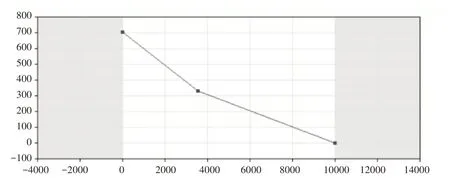
图11 改进后的生产策略
2.3.5 按月规划的生产策略
研究需求发现3月和10月订单数目会激增,可结合以上所有策略设计不同月份的库存策略参数。由于篇幅所限,在此不再展示仿真结果。
3 结语
被装精确申领模式是我军后勤保障历史上的一次重大突破,其质效直接关系到官兵的切身利益,意义重大,影响深远。本文针对申领模式供应链中存在的库存问题,提出相应的改进方法,并利用anylogic软件,对库存策略的效果进行模拟仿真,仿真结果表明,该方法对于提高效率和降低成本作用比较明显,可以为相关部门的策略制定提供一定的思路。
