由质子单粒子效应截面预测重离子单粒子效应截面方法研究

马 旭,韩金华,郭 刚,陈启明,刘建成,赵树勇,张 峥

(中国原子能科学研究院 国家原子能机构抗辐照应用技术创新中心,北京 102413)

航天器在空间中运行时,空间辐射粒子会引起航天器中的电子器件产生单粒子效应(SEE),威胁航天器的安全可靠运行。质子和重离子是引发器件产生SEE的主要辐射粒子[1]。重离子的电离能力强,在器件中直接电离出大量的电子-空穴对,在电场作用下被相应节点收集后产生SEE。中高能质子主要通过其与硅核反应产生的次级离子,如α、Mg、Al等的电离作用引发SEE[2]。质子和重离子SEE物理机理之间的关联为两种粒子的SEE截面相互预测提供了可能性。通常需要对航天器将要搭载的器件开展质子和重离子SEE实验来获取器件的SEE截面,再将SEE截面与空间轨道的辐射环境数据相结合计算得到器件在轨SEE错误率,以此评估器件抗辐射性能[3]。由于成本和加速器机时有限,可以使用一种粒子对器件进行辐照,然后根据实验结果和相互关系对另一种粒子引发的SEE截面进行预测。

由重离子SEE截面预测质子SEE截面的研究开展得较早,已经发展了多个计算模型[4],如Peterson[5]、BGR[6]、Edmonds[7]、Barak模型[8]等。另外,在重离子SEE实验数据的基础上建立器件的平行六面体(RPP)模型,然后进行蒙特卡罗仿真得到质子SEE截面也是一种重要的方法[9]。然而,使用重离子对器件进行辐照前需要将器件开盖,尤其是目前很多先进器件为倒装器件,它们在开盖后还需减薄衬底才能进行重离子SEE实验,这样做既会增加实验成本,也可能损坏器件;并且因为重离子在空气中的射程短,重离子SEE实验需要在真空环境中进行,所以使用重离子辐照前需要对辐照靶室抽真空,较为费时。使用质子进行SEE实验的优点为:由于中高能质子的穿透能力较强,所以使用中高能质子进行实验无需开盖减薄,避免损坏器件;质子辐照实验能在大气中进行,无需抽真空,节省时间。使用质子进行SEE实验不存在上述重离子SEE实验中出现的问题,因此,探索由质子SEE截面预测重离子SEE截面的方法、拓展重离子SEE截面获取途径对评估器件抗辐射性能具有重要价值。

由质子SEE实验截面预测重离子SEE截面的研究开展得较晚,研究成果相对较少。Wrobel等[10]根据重离子和质子入射后敏感节点收集的总电荷和瞬态电流的下降时间与发生SEE之间的关系,利用蒙特卡罗模拟软件MC-Oracle建立由质子SEE截面计算重离子SEE截面的方法。Caron等[11]基于质子SEE实验数据建立器件的RPP模型,并将RPP模型的临界能量和敏感体积的表面积结合Zebrev等[12]的集约模型计算重离子SEE截面,然而集约模型只适用于纳米器件。Barak模型[8]是由重离子SEE截面计算质子SEE截面的公式,将重离子SEE截面与质子核反应产生的次级粒子线性能量转移(LET)谱积分得到质子SEE截面。Galimov等[13]和Chen等[14]以Barak模型为基础建立了由质子SEE截面预测重离子SEE截面的方法,前者将重离子SEE截面随LET的变化关系设为一次函数,通过拟合得到重离子SEE截面,然而重离子SEE截面随LET变化呈一次函数的关系仅适用于纳米器件;后者以等效LET谱替代次级粒子LET谱,将等效LET谱结合质子SEE截面实验数据,计算得到重离子SEE截面随LET变化的Weibull函数。

本文推导由重离子SEE截面计算质子SEE截面的公式,然后利用该公式将由质子SEE截面预测重离子SEE截面的问题转化为解方程的问题,方程的未知数为表征重离子SEE截面随LET变化的Weibull函数的4个参数。根据3款静态随机存储器(SRAM)的质子单粒子翻转(SEU)截面的实验数据,建立质子和重离子SEE截面之间的方程,使用粒子群算法对其求解,获得Weibull函数的参数。

1 质子和重离子SEE截面之间的关系

重离子入射到微电子器件中,主要通过与硅的核外电子间的非弹性散射在器件中沉积能量,同时将能量传递给核外电子,使之电离,产生大量电子-空穴对[15],电子-空穴对会被敏感节点收集,当沉积的能量超过临界能量后,就导致器件产生SEE。质子的电离能力较弱,主要通过与半导体材料(主要是硅)的原子核发生核反应,产生质子、α粒子以及重离子,这些离子也会在器件中沉积能量,从而引发SEE。在文献[14,16]中,定义了等效LET,即:

(1)

其中:Edep为在敏感体积中沉积的能量;ρ为硅的密度;d为敏感体积的厚度。

通过等效LET将1个质子等效为1个的LET为LETeq的重离子,若其进入了敏感体积,则它们在敏感体积中沉积的能量相同。当有Nin个能量为E的质子入射器件时,在敏感体积中沉积的能量有一定的分布,因此在等效为重离子入射时,重离子的LET也存在一定的分布,定义等效LET谱为:

(2)

(3)

2 由质子SEE截面预测重离子SEE截面

若通过实验获得质子SEE截面以及通过蒙特卡罗模拟获得等效LET谱,就可利用式(3)计算重离子SEE截面。通常重离子的SEE截面σHI(L)随LET的变化遵循Weibull函数:

(4)

其中:σsat为SEE的饱和截面;Lth为LET阈值;W为宽度参数;S为形状参数。

由于Weibull函数有4个参数,若能从实验上获得不少于4组质子SEE截面σp(E),就能利用式(3)求出Weibull函数的4个参数,得到重离子SEE截面随LET变化的表达式,即得到重离子SEE截面。

本文选取Cypress公司的2款不同特征尺寸的双数据速率(DDR)-Ⅱ型SRAM[17-19]和文献[20]中的1款SRAM作为研究对象,由质子SEU截面的实验数据预测重离子SEU截面,并将其与重离子实验结果相比较。3款器件的基本信息及质子和重离子SEE实验数据来源列于表1。另外,在北京HI-13串列加速器上对器件B进行了重离子SEE实验,用到的粒子分别为Li、O、Al、Cl,能量分别为40、70、110、150 MeV,相应的LET分别为0.48、3.90、8.93、13.4 MeV·cm2/mg。

表1 本文选取的3款SRAM器件基本信息

2.1 器件RPP模型建立

上述3款器件的质子SEU截面通过实验得到,结果如图1所示。由于器件的实际结构未知,缺少计算等效LET谱的敏感体积厚度,因此使用蒙特卡罗程序Geant4模拟质子入射器件,建立器件的RPP模型,在RPP模型的基础上进行等效LET谱计算。

a——SRAM A;b——SRAM B;c——SRAM C

图2所示为RPP模型,该模型假定器件的敏感体积为处于器件中心的长方体,粒子入射器件并在其中沉积能量,只有在敏感体积中沉积能量且大于临界能量时才会引起器件产生SEE。假设器件全部由硅构成,无其他材料覆盖。根据器件的实际尺寸和存储单元数,将器件单元的尺寸设为10 μm×10 μm×10 μm。

图2 RPP模型

建立器件RPP模型需根据质子SEU截面实验数据假定敏感体积的几何尺寸和临界能量,具体做法为:设定敏感体积表面为正方形,由于约105个质子才能与硅发生1次可足以产生SEU的核反应[21],因此将敏感体积的表面积设为高能质子SEU截面的105倍,敏感体积的厚度和临界能量的初始值取相同特征尺寸器件的经验值[22-24],对于本文的3款器件,敏感体积的厚度经验值范围约为0.25～1 μm,临界能量的经验值范围约为11.25～45 keV。

使用Geant4模拟时使用的物理模型为QGSP_BIC_HP,其中包含电磁相互作用和强相互作用等与质子SEE相关的物理模型。为了缩短模拟时间、减小统计误差,将核反应截面增大2 000倍。模拟时每个能量下的入射质子数为106,在增大核反应截面后,引起的核反应数相当于2×109个质子入射所产生的效果。在Geant4中模拟不同能量的质子辐照,质子从器件表面随机入射,然后统计每个质子入射后在敏感体积中的沉积能量,判断其是否超过临界能量,若超过临界能量则发生SEU,并计算质子的SEU截面,质子SEU截面的计算公式为:

(5)

(6)

其中,N为实验数据点的数目。若MSE小于0.01,则将此时的参数作为器件对应的RPP模型参数,否则就调整RPP模型参数重新模拟质子辐照并计算质子SEU截面,直至MSE小于0.01。

在RPP模型中,临界能量越小,则沉积能量大于临界能量的粒子数目越多,SEU截面越大;敏感体积的表面积越大,进入敏感体积的粒子越多,SEU截面越大;敏感体积的厚度越大,在敏感体积中沉积的能量越多,沉积能量大于临界能量的粒子数目越多,SEU截面越大。因此根据上述原理调整RPP模型参数的过程为:调整临界能量,使质子SEU截面实验值和模拟值的MSE小于0.01,若临界能量不在经验值范围内,就调整RPP模型的表面积和厚度,重复上述过程,直至MSE小于0.01。

最终上述3款器件的质子SEU截面模拟值如图1所示,与实验值较为符合,MSE均小于0.01,其所对应的RPP模型参数列于表2。

表2 3款SRAM的RPP模型参数和MSE

2.2 等效LET谱计算

器件的RPP模型建立后,使用Geant4模拟不同能量的单能质子入射器件,统计敏感体积中的能量沉积,利用式(1)和(2)计算得到不同能量下质子辐照器件沉积能量的等效LET谱。由于质子辐照的是整个器件,产生重离子的位置应当覆盖敏感体积上方器件的整个剖面,因此使用如图3所示的敏感层结构,敏感层的厚度与RPP模型的敏感体积的厚度相同,面积和器件的面积相同。

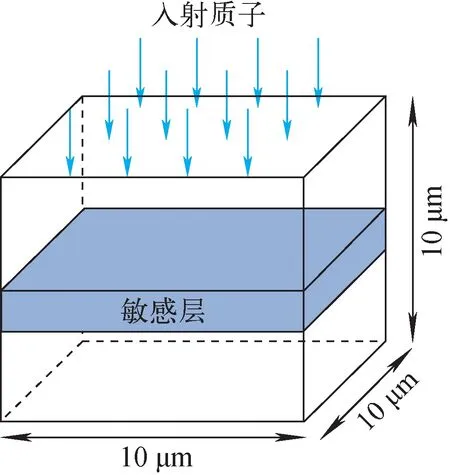
图3 用于计算等效LET谱的敏感层结构

模拟过程中每个能量下入射质子数均为107,并将质子核反应截面增加200倍。在统计过程中,仅统计由核反应产生的次级粒子的能量沉积。由于核反应截面增大,所以统计计数需除以核反应截面增大的倍数。图4为3款器件所对应的等效LET谱。

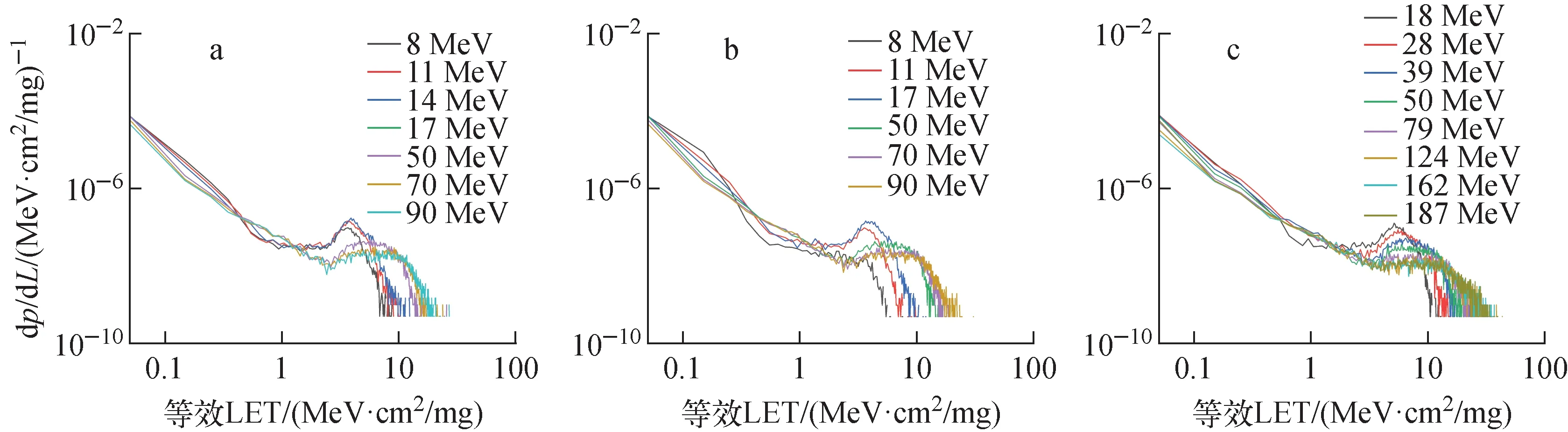
a——SRAM A;b——SRAM B;c——SRAM C

2.3 重离子SEE截面计算

F=∑(σexp(Ei)-σcal(Ei))2

(7)

F越小,质子SEE截面的实验值和计算值越接近,则重离子SEE截面σHI(L)就越接近真实情况。通过迭代算法可寻找F的最小值,当达到最大迭代次数或F小于预设的下限时则停止迭代,否则改变Weibull函数的参数,并按照上述过程重新计算F。停止迭代后得到的Weibull函数的参数即为方程的解,从而得到重离子SEE截面。上述过程将解方程的问题转化为最优化问题,可利用最优化方法求解。

本文采用粒子群算法求解最优化问题,该算法的基本思想是通过群体中个体之间的协作和信息共享来寻找最优解,其在优化函数、神经网络训练中有诸多应用[25-26]。利用粒子群算法求解Weibull函数参数的流程如图5所示。利用该算法计算Weibull函数的参数在初始阶段需要设置待求变量的取值范围。编写程序时,每个个体都代表1个可能的解,对应于空间中的一个坐标,所有个体组成1个群体,代表1组可能的解的集合。由于Weibull函数有4个参数,所以待求变量数为4,每个个体的位置以4维空间中的坐标来表示。

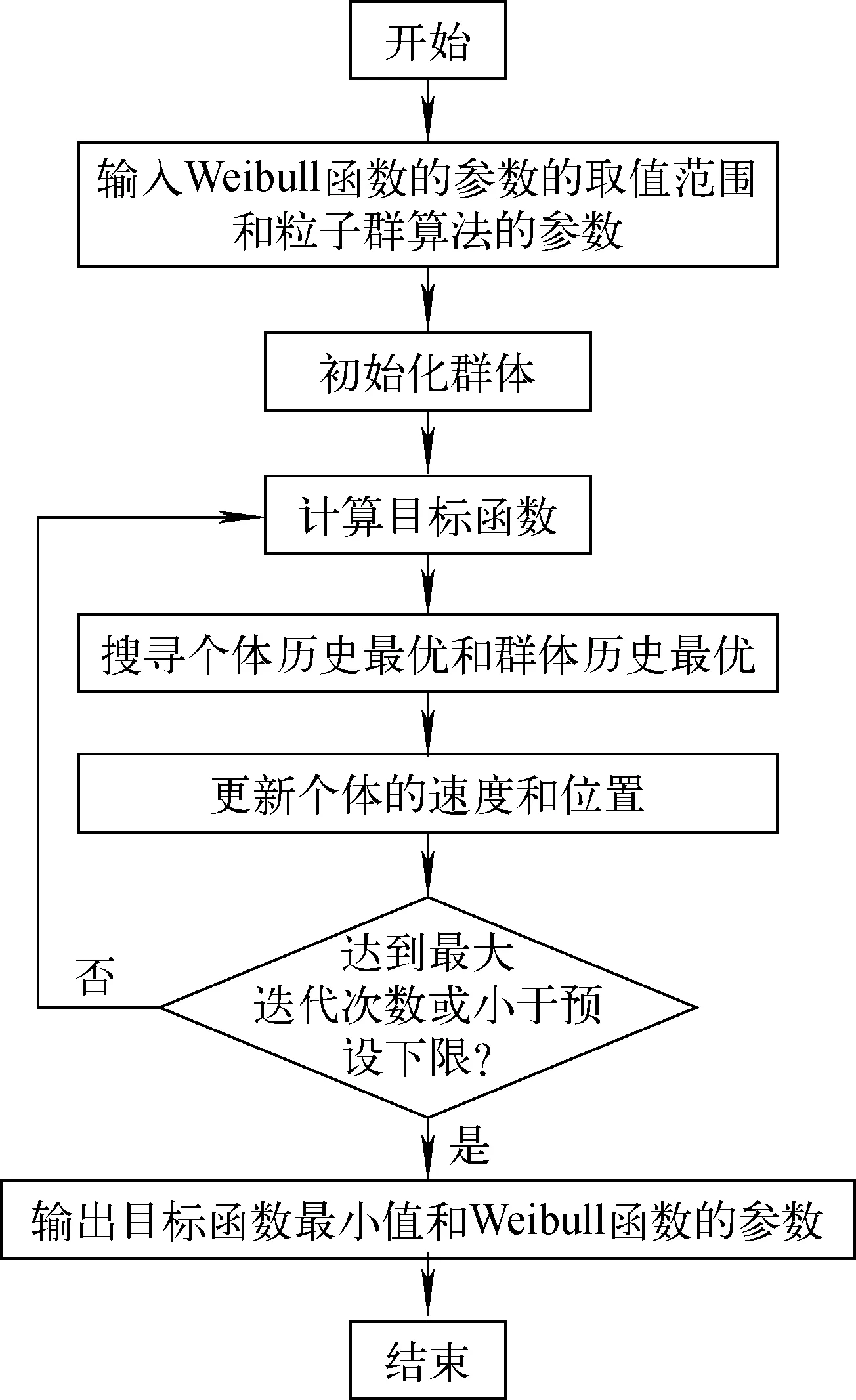
图5 粒子群算法求解Weibull函数参数的流程

根据文献[27]中的公式估算质子SEE截面:

σ(E)=2.4×10-6σsate-δ(E)Lth

(8)

δ(E)=0.134+9/E

(9)

由两个能量E1和E2下的质子SEE截面σ(E1)和σ(E2),联立式(8)、(9)可解出σsat和Lth。当有多个能量下的质子SEE截面时,可建立多组方程组,从而解出多组σsat和Lth。当LET阈值为负时,由于不符合物理实际,所以将Lth为负的这一组解舍弃。通过上述过程能得到多组解,将σsat所有解的最小值和最大值作为粒子群算法中σsat取值的下限和上限。由于质子与硅核反应产生的次级粒子的最大LET约为15 MeV·cm2/mg[28-29],所以将Lth的求解范围设置在[0,15]。W和S共同决定了Weibull函数的形状,根据文献中同类器件的经验值[30-35],将W的取值范围设为[5,50],S的取值范围设为[0.5,5]。在初始化群体的过程中,个体的初始坐标将在预设范围内随机选取。

粒子群算法还需设置算法的参数。将F设为目标函数,粒子群算法是通过迭代寻找F的最小值,并以F的大小作为判别每个个体位置的优劣程度。每个个体在迭代过程中所经历的最好位置和整个群体在迭代过程中所经历的最好位置都会被记录下来,用以后续迭代计算。个体的位置在一次迭代中的变化量称为移动速度,对于第i个个体,移动k步后,下一步的移动速度为:

(10)

(11)

其中,itermax为最大迭代次数,将其设为50。

式(10)等号右边的3项分别为惯性项、自我认知项和群体认知项,分别表示个体对先前自身运动状态的信任、个体本身的思考以及个体之间的信息共享与合作,在这3项共同作用下,实现了个体之间的协作与信息共享。在此速度的基础上,移动后新的位置为:

(12)

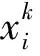
在初始化群体时,群体数量为5,群体之间相互独立,每个群体中有1 000个个体,目标函数的最小值取5个群体计算结果的最小值。计算结束后,输出目标函数F的最小值和对应的Weibull函数参数。3款器件的重离子SEU截面Weibull曲线的计算结果和实验结果如图6和表3所示。

a——SRAM A;b——SRAM B;c——SRAM C

表3 3款SRAM的重离子SEU截面实验值拟合与计算Weibull函数参数的比较

对于SRAM A,在LET为1.7 MeV·cm2/mg处重离子SEU截面计算值和实验值相对偏差为64%,在其余3个LET处的相对偏差均在21%以下;对于SRAM B,在LET为0.48 MeV·cm2/mg处的相对偏差为102%,在其余7个LET处的相对偏差均在22%范围内;对于SRAM C,在LET为0.24、0.30、0.51 MeV·cm2/mg处的相对偏差较大,最大可达1 339%,在其余3个LET处的相对偏差均在32%以下。偏差较大的点大多在低LET范围内,这是由于重离子SEE截面在低LET区间内变化幅度大。其他方法计算的重离子SEE截面和实验值通常也会有数量级的差异[10-13]。总体而言,本文的计算方法达到了较好的效果。

3 结论

本文以质子SEE和重离子SEE机理间的物理关联为基础,推导了由重离子SEE截面计算质子SEE截面的公式。根据该公式,建立了由质子SEE截面预测重离子SEE截面的方法,将由质子SEE截面计算重离子SEE截面的问题转化为解方程的问题。根据3款不同特征尺寸的SRAM器件的质子SEE截面实验数据,利用蒙特卡罗模拟建立了器件的RPP模型,并在RPP模型的基础上使用敏感层结构计算了等效LET谱。在建立RPP模型时根据质子实验数据对其参数进行约束,这样在RPP模型基础上计算的等效LET谱更为可靠。最后将等效LET谱和质子SEE截面实验数据相结合,利用粒子群算法计算表征器件的重离子SEE截面随LET变化的Weibull函数的4个参数,其结果与重离子实验结果一致性较好,验证了计算方法的有效性。

除了硅材料外,在器件中还可能存在原子序数较高的材料,如金属布线层中的钨和钛[36]。质子与硅核反应的最大LET值约为15 MeV·cm2/mg,而与高Z材料核反应产生的次级粒子LET会接近40 MeV·cm2/mg[37]。对于低LET阈值的器件,质子与硅发生核反应贡献了主要的SEE截面,而与高Z材料核反应对SEE的贡献可以忽略;对于高LET阈值的器件,质子与高Z材料核反应贡献了主要的SEE截面。由于本文的RPP模型中仅考虑了硅,所以只适用于计算低LET阈值器件的重离子SEE截面。若通过扫描电子显微镜获得器件的结构、材料等信息[14,36],并构建相应的RPP模型,则该方法将同时适用于高LET阈值的器件。