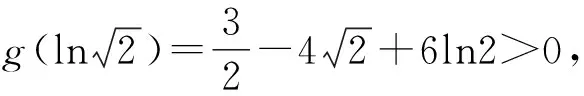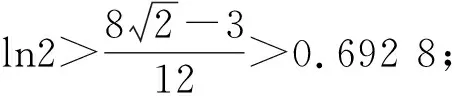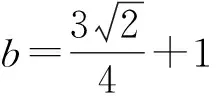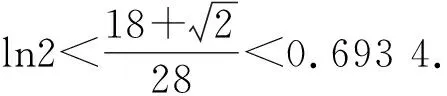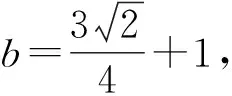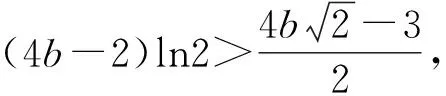基于数学运算素养下的近似值运算问题

晏 鸿

(新疆乌鲁木齐市新疆教育科学研究院,新疆 乌鲁木齐 830049)

《普通高中数学课程标准(2020年修订)》提出:数学运算是指在明晰运算对象的基础上,依据运算法则解决数学问题的素养.主要包括运算对象、运算法则、运算思路、运算方法、运算程序、运算结果六个关键指标[1].其中运算对象是条件,运算法则是规则,运算思路是方向,运算方法是工具,运算程序是蓝本,运算结果是目的. 本文结合高考真题,基于数学运算素养的视角,提出解决近似值运算问题的基本思路,以供参考.

1 理解运算对象,应用运算法则

为突显高考的核心功能,现在的高考卷有一种趋势,便是适当增加融入德智体美劳五育背景的题目.这种题都是以真实问题为情境,然后进行合理的描述,虽然这个情境学生本身不了解或者是超出了学生的能力范围,但题干中会直接给出独立的结论,仅要求在这个结论基础上进行解题.因此理解运算对象、用好独立的运算法则尤为重要.

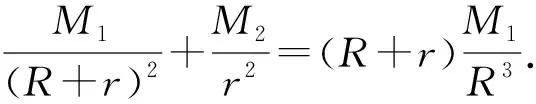
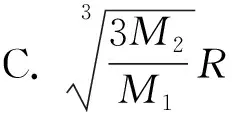
分析解决本题的关键在于能否冷静细致读题,正确理解题意与运算对象,将有关式子变形,建立关于α的等式,运用提供的近似计算结论求解．但由于题干较长,数学阅读理解能力要求较高,再加上考查了近似值运算,属于非常规考查,因此考查难度较大．

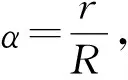
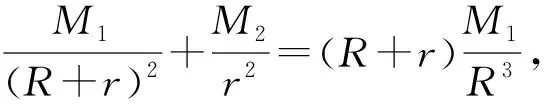
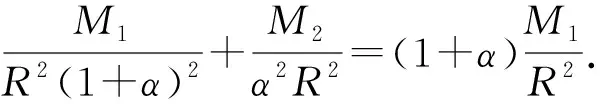
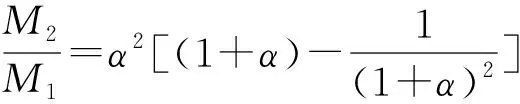
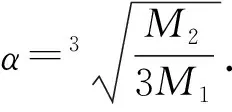
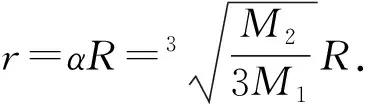
故选D.

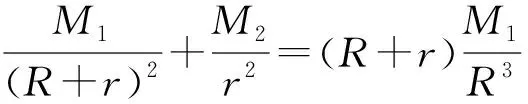
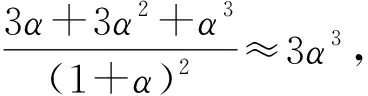
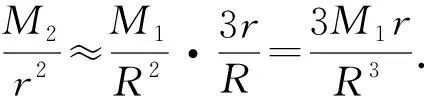
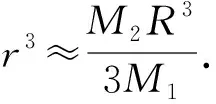
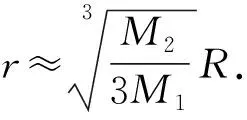
故选D.

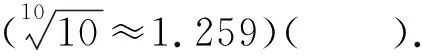
A.1.5 B.1.2 C.0.8 D.0.6

解析由L=5+lgV,得

lgV=L-5=4.9-5=-0.1.

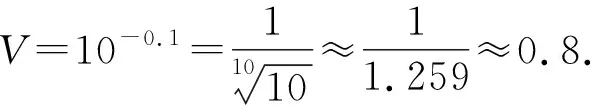
故选C.

评析这类题的解决重在不要被大段的文字所迷惑,本末倒置.要抓住运算对象,理解运算对象的数学问题本质,运用好题目中提供的运算法则.

2 探究运算思路,选择运算方法

代数运算是解决数学问题的基本方法,是数学运算素养的外部表征,是数学能力强弱的反映.提高运算能力更需要优化思维品质,结合感性与理性,关联已知与未知,将方向与方法融合,知识与经验贯通,从运算思路、运算方法入手,选择合理的解决办法.

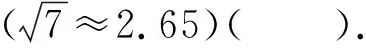
A. 1.0×109m3B. 1.2×109m3

C. 1.4×109m3D. 1.6×109m3

分析本题思维难度不大,只要求出棱台的高,利用棱台的体积公式就可解决,如果体积公式没记住,也可以选择把棱台补成棱锥的方法,此外还要把具体数字算对．

解析如图1,由已知棱台的高为MN=157.5-148.5=9(m),增加的水量为棱台的体积V．

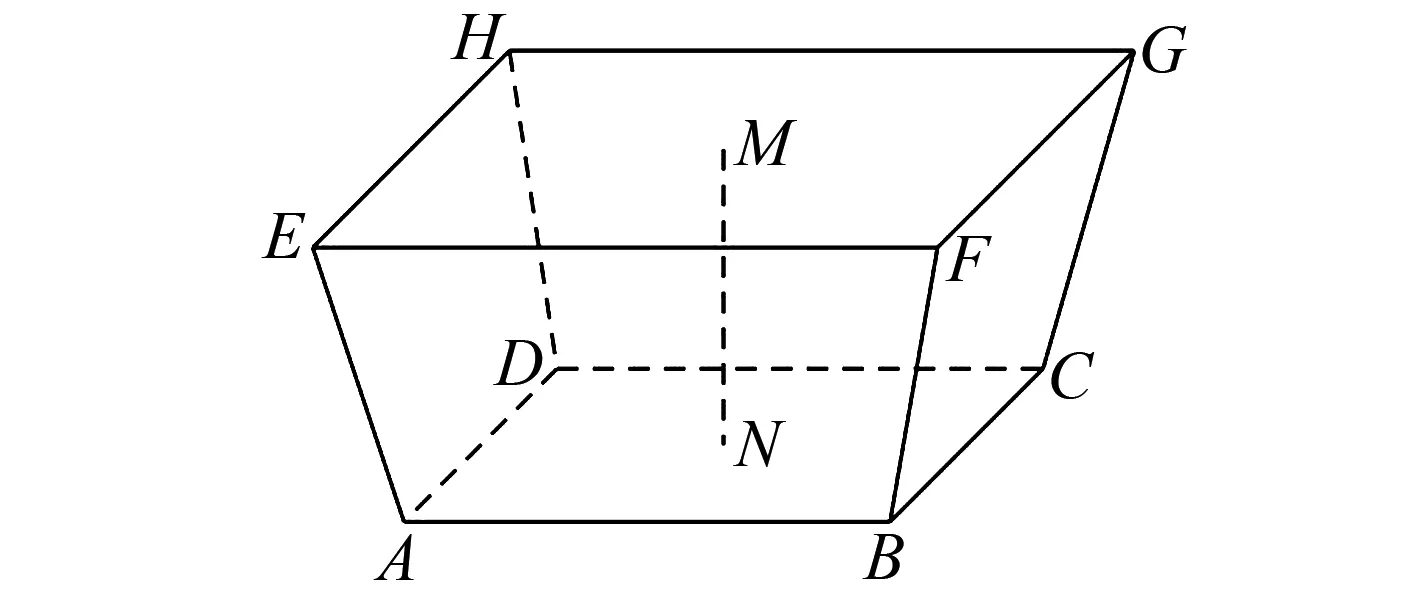
图1 2022年新高考全国Ⅰ卷理4

棱台上底面S=140.0(km2)=140×106(m2),

下底面积S′=180.0(km2)=180×106(m2),

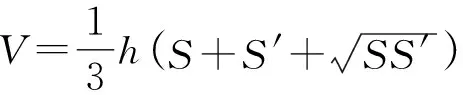
≈(96+18×2.65)×107

=1.437×109≈1.4×109(m3)．

故选C．

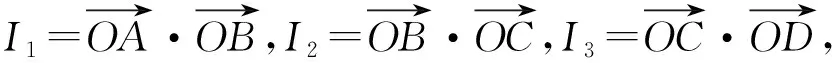
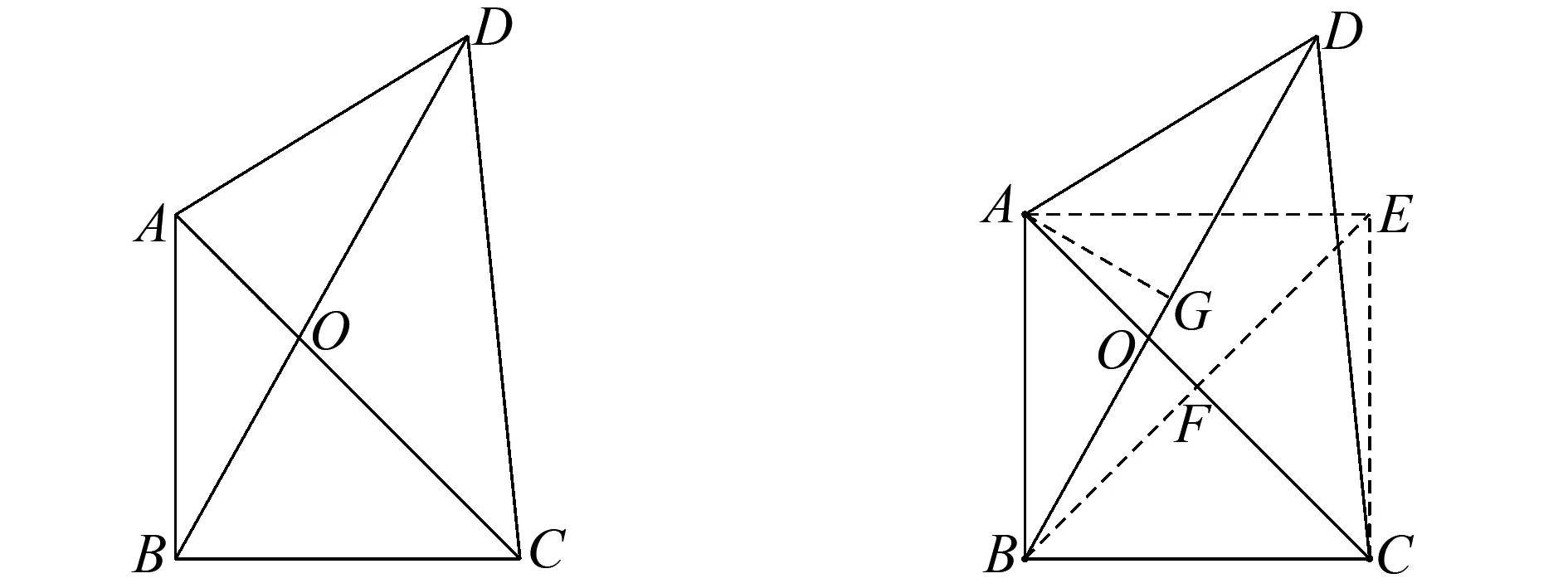
图2 例4题图 图3 例4解析图

A.I1

C.I2

解析如图3,作正方形ABCE,F为正方形的对角线的交点,则∠AFB=90°,∠BOC<90°,∠AOB=∠COD>90°.

又AB=BC,则OA

作AG⊥BD于点G,由AB=AD,

则OB

而cos∠AOB=cos∠COD<0,

所以I3

于是I3

故选D．

评析近几年的高考数学命题对标课程标准,创新考查思路,坚持反套路反刷题,引导中学教学改变机械死板、以练代讲的模式.如例2对棱台体积的考查,既在课程标准的内容范围内,又回避了各种教辅资料上常考的柱、锥和球,用不常规的考题,选拔出真正理解学科知识本质的学生,有利于创新型人才的培养,让高三几本教辅、几张试卷讲到底失效．

3 设计运算程序,求得运算结果

数学运算表面上看是一种数学规律的变化,运算过程只需要遵循运算法则就行,但深层次理解就会发现其中包含逻辑推理的素养,是“逻辑思维与数字计算”的混合体,是演绎推理的一种形式.因此依据逻辑推理,为近似值运算设计最简洁、最有效的运算程序,是运算成功的前提.

例5 (2014年全国Ⅱ卷·理21)已知函数f(x)=ex-e-x-2x.

(1)设g(x)=f(2x)-4bf(x),当x>0时,g(x)>0,求b的最大值;

解析(1)因为g(x)=f(2x)-4bf(x)

=e2x-e-2x-4x-4b(ex-e-x-2x),

所以当x>0时,

e2x-e-2x-4x-4b(ex-e-x-2x)>0.

又g′(x)=2[e2x+e-2x-2b(ex+e-x)+(4b-2)]=2(ex+e-x-2)[ex+e-x-(2b-2)],

2(ex+e-x-2)≥0.

①当b≤2时,g′(x)≥0,即x=0时等号成立. 此时g(x)在R上单调递增.

又g(0)=0,故对任意x>0,有g(x)>0.

综上可知,当b≤2时,对任意的x>0,有g(x)>0,故b的最大值为2.

(2)由(1)知,

所以ln2的近似值为0.693.

总之,对于近似值运算问题,还需要记住一些常见的数,例如:π≈3.141 5,ln2≈0.693 1,e≈2.718 3,sin1≈0.841 5,ln2≈1.099等,否则在近似值运算过程中就可能会找不到头绪.作为高考题,一般都会采用台阶式命题,只要抓住题中隐含的提示,合理运用逻辑推理、数学运算等素养,问题就会迎刃而解.