非导数背景下的函数不等式求解策略
2023-08-30武锦涛
武锦涛
(扬州大学数学科学学院,江苏 扬州 225002)
非导数背景是指在不涉及导数知识下的问题情境,在题目中不会出现明显的导数知识,在具体解题中无法使用或者可以使用但过程极其复杂的情形.在此背景下,函数不等式是函数基本性质中比较常见的考查形式,考查学生的构造能力,数形结合和特殊到一般的数学思想.在解这类问题时,有以下几个难点:第一,如何从题目条件中发现所要考查的知识点,这种不等式形式有何实际意义?第二,如何将这些知识点与题目和已拥有的知识相联系.
1 题目给出具体函数解析式
在高考试题和模拟试题中,一般给出的函数解析式不会复杂到超出认知范围,同时也不会特别简单,一般为几个初等函数的和、差或者乘积形式或者复合形式的运算.

分析这道题虽然给出了函数解析式,但这个函数解析式在进行求导运算时不好判断其性质,这就需要我们分开来看部分函数的性质

又f(x)是奇函数,因此f(x)在R上为减函数.
所以不等式f(2x2-10x)+f(x2-6x-12)<0可化为f(2x2-10x) 可得3x2-16x-12>0. 两式相加,得f(-x)+f(x)=4. 解法1(代数方法)由上述可得 f(-a)+f(a)=4. 由题目条件f(-a)+f(2a-3)>4, 所以f(-a)+f(2a-3)>f(-a)+f(a). 所以f(2a-3)>f(a). 所以a>3. 一些题目条件中给出一部分解析式,给出一些具体条件,但这些解析式通常不能直接用于解题,还需要对题目条件进行分析,找出在全部定义域的解析式或图象,必要时还需要运用构造的方法来建立函数模型. 因为f(x)为R上的增函数, 即ax2-2x+6≥0在x∈R恒成立. 所以f(x)为奇函数.所以f(-x)=-f(x). 所以g(x)为偶函数. 即g(x1) 因为g(x)为偶函数, 所以g(x)在(-∞,0)上单调递增. 因为f(3x)=3f(x),f(1)=1, 解得-3≤x<0或0 所以原不等式解集为[-3,0)∪(0,3]. 在一些题目中,有时完全没有给出解析式,相对于前两种题目来说忽略一些定量的运算转而多了一些定性分析,具有高度抽象性,不易解决,往往是难题. 例5 设f(x)是定义在R上的偶函数,且当x≥0时,f(x)=ax(a>1),若对任意的x∈[0,b+1],均有f(x+b)≥f2(x),则实数b的最大值为____. 分析这道题的条件只给出函数类型为指数函数,没有给出具体的值,蓦然一看不知该从何下手,在不知道具体值的同时还有另一个未知量在“捣乱”,但只要通过分析函数的奇偶性,是能使条件从无到有,甚至还可以求出具体的值,这就是这道题的神奇之处. 解析因为f(x)是定义在R上的偶函数,当x≥0时,f(x)=ax(a>1),所以f(x)=a|x|(a>1),且当x≥0时f(x)单调递增. 所以f2(x)=(a|x|)2=a|2x|=f(2x). 即|x+b|≥|2x|.即3x2-2bx-b2≤0对于任意的x∈[0,b+1]恒成立[3]. 即3(b+1)2-2b(b+1)-b2≤0,b+1>0. 例6 定义在R上的函数f(x)满足f(xy)=f(x)+f(y),当x>1时,f(x)<0,则函数f(x)的零点个数为____. 分析这道题的已知条件非常简单,只给了一个抽象函数的式子,一个局部函数不等式,关键的突破点就在于这个抽象函数不等式到底怎么用,所对的那个条件应该和前面的式子怎么结合起来成为解决这个问题的关键,一般这类抽象函数的问题通常采用的方法就是赋值,通过赋值找到题目关联条件然后得到答案. 解析令x=y=0可得f(0)=f(0)+f(0). 从而f(0)=0. 令x=y=1,得f(1)=f(1)+f(1).从而f(1)=0. 令x=y=-1,得f(1)=f(-1)+f(-1)=0. 令y=-1,可得f(-x)=f(x)+f(-1). 所以f(-x)=f(x),即f(x)为偶函数. 所以f(x)在(0,+∞)上单调递减,且只有x=1一个零点. 因为f(x)为偶函数, 所以f(x)在(-∞,0)上单调递增. 所以f(x)在(-∞,0)也只有一个零点x=-1. 故f(x)有3个零点. 函数不等式是高中数学知识里面较为重要的一部分,也是常考的经典题型,但近年的高考这类型题更加综合、抽象,同时伴随着较大的计算量,较复杂的分析过程,较为新颖的知识复合.因此在学生掌握这类解题技巧和思维方法的同时,将知识点与解题技巧进一步融合内化,为以后的高考函数不等式的问题打下坚实基础.
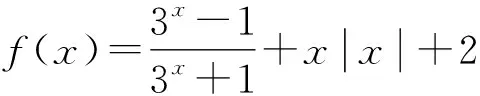
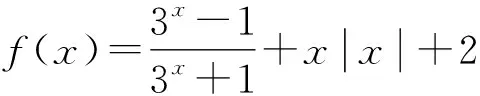


2 题目给出部分函数解析式

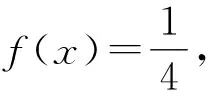





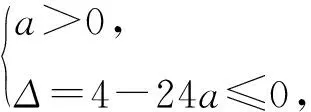



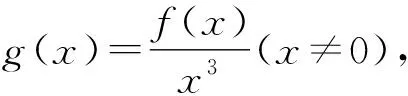



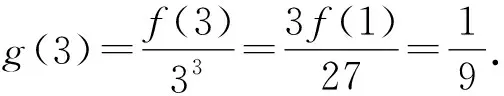
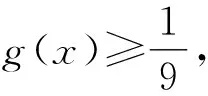
3 题目未给出具体解析式