基于Burgers向量提取与分析的改进PRD算法在位错环模拟中的应用
2023-08-29徐鑫铖聂宁明贺新福张纪林
徐鑫铖,聂宁明,王 瑾,贺新福,曾 艳,张纪林,王 珏,万 健,*
(1.杭州电子科技大学,浙江 杭州 310018;2.中国科学院 计算机网络信息中心,北京 100190;3.中国原子能科学研究院,北京 102413)
体心立方体(BCC)铁及其合金的辐照实验形成的各种位错环[1]及其演化过程,对于各种核能系统(如裂变和聚变反应堆)中使用的结构材料的力学性能(如辐照脆化、硬化、膨胀、蠕变等)有重大影响[2]。国内外针对这一热点问题已开展多年研究。Marian等[3]以及Xu等[4]采用传统分子动力学(MD)着重分析了〈100〉间隙环的形成和生长机制。Chen等[5]采用透射电子显微镜观察到了位错环的不同惯习面。Gao等[6]通过自研的自适应加速分子动力学(SAAMD)方法进行模拟,提出位错环惯习面在位错环转变过程中的一系列变化。
BCC铁及其合金在辐照后产生的主要位错环类型,分别是1/2〈111〉环和〈100〉环,且两者所占比例相当[3]。针对1/2〈111〉和〈100〉位错环能量的研究[3-6]显示,1/2〈111〉环在能量上会更加受到青睐。但是,实验中却发现同时存在一定数量的〈100〉环。经研究发现[7],对于小尺寸的〈100〉位错环来说,转变到1/2〈111〉位错环所需要跨越的势垒不是很高,通常在纳秒尺度就可以看到转变的现象。然而,考虑到大尺寸〈100〉环或者含有溶质元素的〈100〉环[6-8],其能量有可能低于同尺寸的1/2〈111〉位错环。基于这些原因,有关不同类型位错环的形成与转变过程目前还模糊不清,而不同类型的位错环可能会导致不同硬化现象,且〈100〉位错环由于不稳定,的确会发生转变为1/2〈111〉位错环的现象,因此研究1/2〈111〉和〈100〉位错环的转变十分重要。
加速分子动力学(AMD)是一种扩展分子动力学模拟时间尺度的方法[9],常见的AMD方法有并行副本复制法(PRD)[10]、温度加速法(TAD)[11]以及超动力学法(HD)[12]等。相对于MD模拟,AMD方法可以将模拟的时间尺度提高几个数量级,从而可以观察到更多重要的现象。
然而,AMD方法都具有一定局限性,在针对少数特定的模拟实验时,往往会由于加速原理与实验的物理特性不兼容,导致不能有效地在时间尺度上进行扩展,或者由于加速导致很多短暂的现象无法被捕捉。对〈100〉位错环以及1/2〈111〉位错环之间形成和转化机制的模拟实验就是一个例子。因此本文结合位错环转变时的一些机理特性[13],对PRD算法进行改进,使其加速效果能够适用于位错环转变的模拟。
本文对于PRD算法改进的核心思想在于:PRD算法对于模拟中状态改变事件的判定标准是否合理。Lammps[14]中实现的PRD算法只是单纯根据系统中原子的偏移量是否达到一个阈值来判断事件是否发生,然而由于在模拟位错环转变的实验中,位错环本身的扩散现象也会使原子不断发生偏移[15-16],而位错环的扩散对于观察到位错环转变这一现象来说是没有意义的。真正需要捕捉的现象是位错环的旋转而不是扩散[16],但PRD算法无法单靠原子的偏移量来区分扩散现象与旋转现象。因此,在使用PRD算法对位错环进行模拟的实验中,模拟的精确性受到很大程度的影响,严重影响了对于不同类型位错环形成和转变机制的研究。
本文通过分析位错环转变时的特征,注意到位错环的转变往往伴随惯习面的变化[17],而惯习面的方向与其对应的伯格斯(Burgers)向量有关[18-19]。这也就意味着如果提取并分析出位错环的Burgers向量在模拟中的变化情况,就可以把这种变化作为PRD算法判定一个事件是否发生的依据,以此来对PRD算法做出相应的改进,从而使其能够很好地对位错环模拟的实验进行时间尺度上的扩展。
1 PRD算法介绍
虽然目前MD借助并行计算可对一些系统进行有效处理[20],但对很多经典系统来说,它们的特点是在某个状态进行长期的停留,偶尔才会发生状态的跃迁[10],这就使得MD需要在这些长期停留的状态上计算大量时间步长,对MD算法和计算资源都提出了挑战。因此如何有效利用并行计算机的能力在时间尺度上对模拟实验进行高并行效率的扩展成为关键。PRD算法就是通过将系统复制成多个副本,每个副本使用不同的处理器分别进行模拟。根据过渡态理论(TST),并行运行多个独立的轨迹可以给出从一个状态到另一个状态的精确动力学演化[21-22]。因此PRD算法在针对小型罕见事件的系统动力学研究中,能够有效地将时间尺度进行大幅扩展。
1.1 PRD算法原理
考虑一个经典的分子动力学系统,该系统的某个状态可能有多种逃逸路线(nesc)跃迁到另一个状态。在发生状态跃迁后,系统将会有一段时间(tcorr)记住它是如何进入到新状态的,并且可能会有动态相关的表面交叉。但同样的,当超过tcorr,轨迹对其如何到达新状态没有记忆。从新状态中找到特定逃逸路径的概率是无偏的。而由于到下一次逃逸的等待时间远大于系统的记忆时间,因此在模拟过程中,许多的独立尝试跃迁都是为了找到逃逸路径,即单位时间内的成功概率是1个常数,形成了1个1阶过程。将ktot定义为从该状态寻找下一条逃逸路径的总速率常数,下一个事件发生前等待时间的概率分布P(t)为:
P(t)=ktotexp(-ktott)
(1)
式中,t为从当前状态到下一个事件发生前的等待时间。
系统的模拟可用以下方式总结[10]:假设自轨迹进入当前状态以来,已经经过了tcorr,因此由式(1)能给出下一次跃迁发生前的准确等待时间分布。当跃迁确实发生时,在主事件的瞬态时间tcorr期间,轨迹可能会执行与主事件相关的附加状态到状态转换,之后它会在某个状态下热化,并且循环再次以新状态的ktot开始。
为了充分利用并行计算机的性能,考虑在M个不同的处理器上模拟同一个系统的M个副本。每个副本在相同状态下开始,但轨迹的初始条件不同,因此副本在统计上是独立的。其中最为关键的一点是:这M个副本的作用与一个具有M×nesc逃逸路径的超级系统相同。修改式(1)以考虑逃逸路径数量的增加和新的总逃逸率(M×ktot),得到了该超级系统的逃逸时间概率分布,以处理器1上的等待时间t1为例,其概率分布Psuper(t1)为:
Psuper(t1)=M×ktotexp(-M×ktott1)
(2)
实际上这也是在任何处理器上发生下一个事件之前的等待时间概率分布。如果给定一个时间点,所有副本上轨迹的累计模拟时间tsum与t1之间的关系为:
tsum=M×t1
(3)
又根据积分性质:
(4)
将式(3)、(4)代入式(2)中,最终可以得到:
Psuper(tsum)=ktotexp(-ktottsum)
(5)
式(5)表明了由M个独立副本并行模拟的超级系统的等待时间概率分布。虽然每次发生转变之后,ktot都会发生变化,但在单个处理器上至少模拟tcorr后,将会得到新状态下的正确等待时间的概率分布。另外,并行化对不同可能逃逸路径的相对概率没有影响,因此以该种方法进行模拟的状态顺序以及发生转变的时间与使用单一副本模拟的结果是非常接近的。
1.2 PRD算法模拟过程
使用PRD算法对系统进行模拟的完整过程如图1所示。系统在每经过一个完整循环之后,时钟将会被提前为M×tevent+n×tcorr,其中:n为去相关的次数;tevent为系统在发生新的事件之前等待的时间。而实际经过的时间则为tevent+n×tcorr。由此可以发现如果tevent远大于tcorr,且每次转变之间的时钟比副本间的通信时间大得多,那么整个过程将会是高效并行的。

图1 PRD算法模拟的过程
最后考虑处理器速度在时间上不恒定的情况。由于式(5)以及1阶过程的特点,在尚未发生转换的任何时间点(tp),从tp测量的等待时间的未来概率分布与从t=0测量t时的归一化指数函数相同。所以PRD方法对于单个处理器速度的任意波动都是有效的。
2 Burgers向量
根据Frank[23]提出的理论,位错可以通过Burgers环路来识别,即给定闭合路径C,封闭位错缺陷的Burgers向量b定义为弹性位移场的线积分:
(6)
式中:Ue为该空间配置下的弹性位移矢量场;C为闭合路径,为该空间下原子到原子的路径;l为闭合路径C上的曲线。
2.1 Burgers向量与位错环惯习面的关系
根据位错环的一些特性以及模拟,当位错环发生转变时,位错环的惯习面往往也会伴随着一定的变化。位错环惯习面的研究指出[6-17],在〈100〉与1/2〈111〉环转变过程中,可能的惯习面方向有:{1 1 1}、{1 1 0}、{2 1 1}以及{1 0 0}。
Gao等[6]对不同尺寸的〈100〉环进行了模拟,其中5个间隙原子构成的〈100〉环,在250 K时进入中间状态,然后随着温度逐渐增加到约400 K,降低系统势能0.55 eV。而对于9个间隙原子构成的〈100〉环,在MD模拟中可发现,环改变了惯习面,从{1 0 0}到{1 1 1}并且对应的Burgers向量从〈100〉转变到了1/2〈111〉。因此,这些模拟结果可以证明,1个〈100〉位错环是可以通过间隙重排的方式,使得惯习面发生变化并导致Burgers向量转变,最终使整个位错环转为1个1/2〈111〉环。
2.2 Burgers向量的提取与位错识别
根据晶体界面中位错的自动识别和索引中提出的算法[24-25],要通过Burgers向量实现位错的自动识别,需要保证闭合路径C中刚好包括单个位错。此外,还需假设1个理想的完美晶格,令其原子到原子的理想路径为ΔX。构成实际Burgers向量的闭合路径C中原子到原子的路径设为Δx,需要将实际路径映射到理想路径,即完成Δx→ΔX的映射,从而显示出由位错引起的不兼容位移并确定其Burgers向量,最终达到自动识别位错的功能。

在确定每一个向量Δx后就需确定闭合路径C。通常缺陷晶体由1个或多个良好区域组成,其中嵌入了1个或多个不良区域。这些不良区域与晶体缺陷(位错和其他)的核心有关。如果两个Burgers环路位于同一个良好区域内,且其中1个环路可以连续转换为另一个环路而不破坏环路本身或使其穿过区域边界,则称其为等效的。两个等效的Burgers环路包含的位错是相同的。当且仅当环路的最短等效环路完全包含在良好区域和不良区域之间的边界内时,环路包含单个位错线。而本文采用的位错识别算法为了得到最精确的解,必须是针对于不可约的环路,从而确保算法能够识别出每个单独的位错段。
通过计算划分出晶体的良好区域与不良区域,并且保证上述两个条件均满足之后,可以得到合适的Burgers环路以及环路上的每一个不可再细分的向量Δx。该算法利用这些向量构成一个个三角网格面,然后沿着环路依次扫描网格面,并不断计算当前位错段。最后该算法将找到晶体中每一个不同的位错段,并将那些可以连接在一起的位错段进行整合,使其转换为1条连续的位错线。
3 PRD算法的改进
本文基于Lammps[14]中对于PRD算法的实现,整合OVITO[26]中位错的自动识别和索引的实现,利用PRD算法每隔一段时间检测当前位错环的Burgers向量是否发生变化,从而准确捕捉到位错环的每一次转变现象。
目前在Lammps中的PRD算法实现逻辑是:首先由用户指定PRD算法的检测间隔、去相关时间以及原子偏移量,接着PRD算法将会根据用户设定的参数,每隔固定的时间将整个系统中每个原子的位置坐标进行记录,并且与上一个事件发生时所记录的原子坐标做比较,如果此时系统中存在任意一个原子的偏移量超过用户所设定的阈值,则会被认为发生了事件。由于PRD算法是采用多个副本并行模拟的方式,因此在这些副本中,可能在同一时刻会有多个副本都检测到了事件的发生,那么此时PRD算法将会随机选中一个副本进行去相关,最后再循环整个过程。
然而,由于位错环的扩散现象,这种判定事件的方式在针对位错环模拟的实验中,会遇到如图2所示的问题。最终导致整个模拟在无意义的方向进行了大量时间尺度的扩展,而位错环的惯习面可能完全没有改变过,更不会出现位错环转变的现象。

图2 PRD算法在位错环转变模拟中遇到的问题
因此本文针对Lammps中PRD算法对于事件判定的逻辑做出改进。基于OVITO中提供的位错自动识别和索引的算法,重新定义了PRD算法检测事件是否发生的逻辑。具体流程如图3所示。其中在对四面体进行分类时,如果1个四面体的6条边都能完成原子实际路径到原子理想路径的映射,则被定义为1个良好四面体,否则认为是1个不良四面体。最后,在对由不良四面体构成的不良区域进行扫描时,为保证Burgers环路为包含单个位错的不可约环路,采用递归算法进行长度递增的选取方式。当计算出Burgers向量不为0时,即确定1个不可约的环路。在按照这种方式对所有不良区域完成扫描之后,就可以得到当前系统空间中的所有位错段。

图3 位错识别算法流程
为了更好地定义PRD算法判定事件的依据,根据不同时刻系统中存在的位错段类型,将系统状态划分为3个阶段:1) 系统只存在〈100〉位错环;2) 系统同时存在〈100〉与1/2〈111〉位错环;3) 系统只存在1/2〈111〉位错环。
上述3个阶段分别对应设置的FLAG的3个不同值。每当Lammps获得位错检索的结果后,会更新对应的FLAG,以此来一一对应上述3个阶段。在模拟实验刚开始时,系统的初始配置为只存在〈100〉位错环,此时FLAG=0。随着模拟的进行以及PRD算法定时地检测,当系统中出现了1/2〈111〉的Burgers向量时,将此时系统的FLAG设置为1,同时开始等待〈100〉位错环完全变成1/2〈111〉环现象的发生。最后当系统中的〈100〉环完全转变到1/2〈111〉环之后,FLAG将会被更新为2。
为了达到更好的加速效果,进一步使PRD算法每次检测的事件均有利于从〈100〉环转变到1/2〈111〉环。在FLAG=1阶段,对1/2〈111〉的Burgers向量占系统总Burgers向量的比例进行统计和分析,从而细化此阶段,如图4所示。在每次检测时,都会将本次副本中检测到的系统的1/2〈111〉Burgers向量所占比例与上一次事件发生时的比例进行对比。如果高于上一次的比例,说明此时系统中位错环惯习面发生旋转而改变的程度更大,因此可以被认为是更倾向于发生完全转变的状态。基于这点,将这种情况也作为PRD算法对于事件是否发生的一个判定依据,从而避免了模拟系统可能长时间停留在FLAG=1阶段,最终导致加速效果不理想的问题。
4 实验
为了评估改进PRD算法的模拟效果,本文针对25个和49个间隙原子构型以及含有Ni溶质元素的〈100〉位错环分别进行了数值模拟实验。实验中采用的Lammps版本为3Mar20。
4.1 25个间隙原子构型〈100〉环模拟实验
采用改进PRD算法对25个间隙原子构型的〈100〉位错环进行模拟转变实验。体系中的box尺寸为5.711 nm×5.711 nm×5.711 nm,原子总数为16 025。采用的势函数来源于文献[27],一种嵌入原子势形式的铁原子势函数。为了评估改进PRD的并行效率以及并行规模的可扩展性,分别在1 000 K的条件下,以10、30、50、70、100个副本进行数值模拟,且每个副本均采用32个进程处理。最终得到的实验结果列于表1,其中每个时间步长为0.01 ps。

表1 采用改进PRD算法的25个间隙原子构型〈100〉位错环的模拟结果
为了评估改进PRD算法的加速效果,使用MD在同样1 000 K条件下,对相同25个间隙原子构型的〈100〉位错环进行模拟转变实验。在使用不同的随机数对速度进行初始化并输出模拟结果后,发现在MD模拟下25个间隙原子构型的〈100〉位错环基本将会在400 000到600 000个时间步长发生转向1/2〈111〉位错环的现象。根据表1的结果,可以看到发生转变时所需的实际步数远小于MD模拟结果。并且随着副本数增加,系统所需要模拟的实际步数越来越少,这也就意味着加速效果随副本数的增加有所提高。因此可以认为改进PRD算法对25个间隙原子构型的〈100〉位错环转变模拟有明显的加速效果,且随着副本数增加,加速更加明显。
4.2 49个间隙原子构型〈100〉环模拟实验
采用改进PRD算法对49个间隙原子构型的〈100〉位错环在1 000 K下进行模拟转变实验。体系中的box尺寸为11.421 nm×11.421 nm×11.421 nm,原子总数为128 049。采用的势函数仍是文献[27]中的铁原子势函数。计算过程中体系自由能变化如图5所示,可以看到体系总能量随步数增加趋于稳定,证明整个计算是收敛的。

图5 49个间隙原子构型的位错环在模拟过程中自由能的变化
在模拟过程中,除与模拟小尺寸的位错环一样,依然保持较好的加速效率外,还看到一些在MD和原PRD算法模拟过程中无法观察到的现象。采用开源可视化工具OVITO的位错提取算法功能(DXA)进行可视化分析,得到的结果如图6所示。根据对实验输出的系统中原子的信息进行可视化分析,发现在转变过程中,会出现〈100〉位错段与1/2〈111〉位错段共同存在的现象。

图6 49个间隙原子构型的位错环中〈100〉与1/2〈111〉位错段共存
4.3 含有Ni元素〈100〉环模拟实验
对含有Ni溶质元素的〈100〉位错环在1 000 K下进行了模拟实验。所用的构型为:先以Ni原子随机分布为初始状态,然后进行蒙特卡罗方法模拟偏聚后得到的构型。体系中的box尺寸为5.711 nm×5.711 nm×5.711 nm,原子总数为16 025,Ni原子数为165,Fe原子数为15 860,Ni的含量为1.03%。初始构型如图7所示。采用的势函数来自于文献[28]的三元Fe-Cu-Ni多体势。

图7 含有Ni元素的〈100〉位错环初始构型
计算过程中自由能的变化如图8所示,随着步数增加体系总能量趋于稳定,因此证明整个计算过程是收敛的。此外,在实验过程中,除经常看到〈100〉位错段和1/2〈111〉位错段共同存在的现象,还多次观察到位错环完全转变到1/2〈111〉环,这在之前的实验中未观察到。采用OVITO的DXA功能对位错进行可视化分析,得到的结果如图9所示。
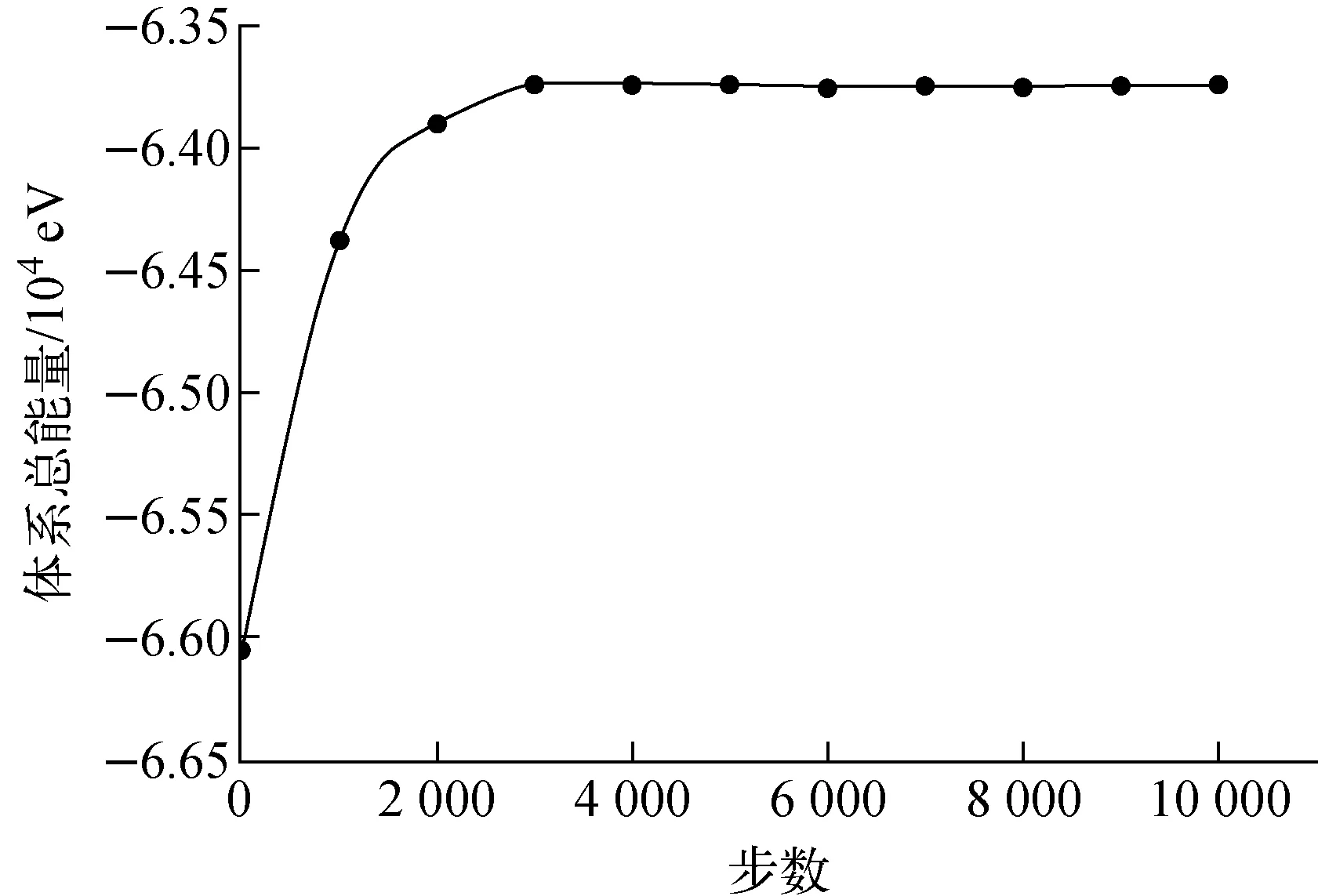
图8 含有Ni元素的位错环在模拟过程中自由能的变化

a——〈100〉与1/2〈111〉位错环共存;b——完全转变1/2〈111〉位错环
5 正确性验证与加速对比
为验证改进PRD算法的正确性,分析了采用MD对25个间隙原子构型的〈100〉位错环的模拟结果,对其在观察到转变时模拟的步数按照每一步时间步长代表0.01 ps进行换算,得到其转变时间在0.4~0.6 ns左右。根据表1对在不同副本下采用改进PRD算法观察到转变的加速步长进行同样的换算后,得到的物理时间和MD所需的物理时间十分接近,也符合小尺寸〈100〉位错环能够在较短时间内发生向1/2〈111〉位错环转变的机理特性,从而在一定程度上验证了改进PRD算法在模拟位错环转变实验中的可行性与有效性。
另外,相对于原PRD算法,本文改进的重点在于对事件的判定与捕捉。通过分析位错环的特性以及位错环在转变时惯习面等特征的变化,并以此来重新定义PRD对事件的判定,来实现PRD算法对每一个事件的捕捉都有利于整个位错环发生转变这一目的。考虑到PRD算法本身基于TST,Voter[10]针对Cu(100)表面空位扩散模拟实验证明了通过副本并行这一方式进行加速模拟的准确性,因此本文研究的改进PRD算法无论是在原理上还是在针对位错环模拟的实践性上都具有一定支撑。
对于加速以及并行效率方面的评估,由于MD以及原PRD算法在针对大尺寸或含有Ni溶质元素的〈100〉位错环的模拟实验中,无法看到一些重要现象,从而导致无法进行有效对比。因此,仍然以对25个间隙原子构型的〈100〉位错环的模拟实验来分析。
首先根据之前MD对25个间隙原子构型的〈100〉位错环的模拟结果,可确定在1 000 K的条件下,转变到1/2〈111〉位错环这一现象将会发生在0.4~0.6 ns左右。接着采用原PRD算法在相同条件下以10、30、50、70、100个副本进行加速模拟,同样每个副本均采用32个进程来处理,并且记录了系统在观察到转变时模拟的实际步长以及加速后的步长,结果列于表2,其中每一个时间步长为0.01 ps。
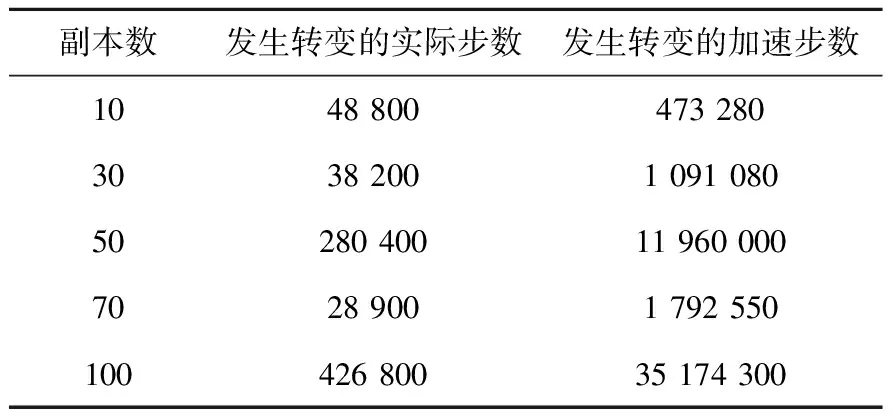
表2 采用原PRD算法的25个间隙原子构型〈100〉位错环的模拟结果
由表2可见:对于观察到转变所需的实际步数,在副本数很小的情况下所需实际步数与改进PRD算法相差不大;当副本数增加时,其所需实际步数非但没有减小,反而有明显的增加,而且还出现了非常不稳定的现象。这与PRD算法预期能够达到的加速效果相差甚远。
此外,当把每个副本下观察到转变所需的实际步数经过PRD算法在时间尺度上进行扩展之后,得到的加速后的实际步数按照每个实际步数代表的物理时间进行换算,发现除了副本数为10的情况,其余情况所需要模拟的物理时间远大于采用MD所需要的物理时间。这与在1 000 K温度下,小尺寸〈100〉位错环实际转变到1/2〈111〉位错环所表现出来的物理特性存在严重偏差,极大地影响了位错环模拟实验的准确性。
对比表1结果,可以看到改进PRD算法对本实验有明显的加速效果,且该加速效果会随着副本数增加变得更加明显。为了更好地对比原PRD和改进PRD算法在不同副本数下的并行效率,以25个间隙原子构型的〈100〉位错环实际转向1/2〈111〉位错环所需的平均最晚时间为标准(0.6 ns),重新对原PRD算法的加速后时间进行校准,并分别计算出两种方法相对于理想加速情况下的并行效率,结果列于表3。

表3 原PRD算法与改进PRD算法的并行效率
由表3可见,在相同副本数的情况下,原PRD算法相对于理想情况下的并行效率均小于改进PRD算法。随着副本数增加,原PRD算法的并行效率下降得非常明显,而改进PRD算法随着副本数增加,仍能保持较良好的并行效率,其中除100个副本的情况,其余并行效率在相对于理想情况时,均能维持在90%以上。这也证明了相较于原PRD算法,改进PRD算法除了能更加准确地加速位错环转变模拟实验之外,在并行性上也有很好的表现,可以应用于更大规模的并行计算上,从而在时间尺度的扩展上达到更明显的效果。
6 总结与展望
本文对PRD算法的原理和过程以及Burgers向量对于位错环的关系和如何提取进行了介绍。通过分析原PRD在模拟位错环转变实验中遇到的问题,结合位错环本身的机理特性,对PRD算法进行改进,并通过实验验证了改进的可行性与有效性。实验结果显示改进PRD算法在针对位错环转变实验具有明显的加速效果,以及在并行性上也具有良好的扩展性。此外,在针对大尺寸以及含有Ni溶质元素的〈100〉位错环模拟实验中,能够捕捉到一些持续时间很短但是同样具有重要意义的现象,帮助更好地理清不同类型位错环的形成与转变过程。
但改进PRD算法仍存在一些不足,因为只是模拟1/2〈111〉和〈100〉位错环转变,因此本文并未考虑位错环合并以及更复杂的演化。且由于采用的是在模拟过程中调用位错检测算法的方式同步分析Burgers向量的变化,对于计算性能有一定的消耗。在针对原子数量较多的大规模模拟系统中,由于计算机性能的限制,在时间尺度上的扩展将会有一定限度。为了更加高效地利用计算资源,对大规模系统也能有较好的表现,改进的PRD算法需在下一步工作中继续展开研究。
