基于分布估计算法优化极限学习机的干旱预测研究

周靖楠 徐敏 龚宇 刘振男 丁怀超

摘要：构建适用的干旱预测模型是保障用水安全与粮食安全的关键。针对极限学习机在干旱预测中存在稳定性差等问题，构建了分布估计算法优化极限学习机模型。基于海温指数优选出关键模型输入，以标准化降水蒸散发指数作为模型输出，对贵州省的干旱情势进行了预测。结果表明：标准化降水蒸散发指数是评价贵州省干旱的有效指数；海温指数是预测贵州省干旱的有效变量，且其具有良好的前兆指示作用，最大提前期长达15个月；同等条件下，分布估计算法优化极限学习机的预测效果优于遗传算法优化极限学习机，该模型可为贵州省的抗旱减灾工作提供技术支撑。

关键词：干旱预测； ELM； EDA； 贵州省

中图法分类号：TV124

文献标志码：A

DOI：10.15974/j.cnki.slsdkb.2023.07.001

文章编号：1006-0081（2023）07-0008-07

0 引 言

干旱是中国用水安全与粮食安全的主要威胁。众多专家学者围绕干旱问题展开了一系列研究工作，而在干旱预测研究方面，基于神经网络的干旱模型构建研究已成为当前热点［1］。极限学习机（Extreme learning machine，ELM）作为一种单隐层前馈神经网络，其主要贡献是解决了传统神经网络隐含层数目难以确定的难题，但其仍存在传统神经网络固有的不足，即初始权值与阈值采用随机方式生成，造成运行结果不稳定、鲁棒性差等问题［2-3］。为此，Han，王杰等［4-5］利用粒子群算法对极限学习机进行了优化改进，以提高模型的稳定性与鲁棒性；Zong 和Liu 等［6-7］分别提出基于加权方法的极限学习机与多核极限学习机，结果表明改进后的模型在性能上有所提升；王杰等［8］提出了一种基于小波核函数的极限学习机，同时为小波核极限学习机的实际应用提供了理论基础；同时，王杰等［9］还运用烟花算法优化了极限学习机，并成功应用于光伏发电输出功率的预测。其他诸如鱼群、自适应差分进化算法均被应用于极限学习机模型的改进工作当中，并且都取得了较好的预测效果，尤其是遗传算法优化极限学习机模型，其预测精度更佳［10-13］。分布估计算法（Estimation of distribution algorithm，EDA）作为一类新型的进化算法，其进化方式与遗传算法类似但又有所不同。相比于遗传算法的进化过程，分布估计算法放弃了交叉、变异等算子的操作，取而代之的是建立了相应的概率模型对解空间的分布进行描述，从宏观的角度对种群进行进化选优。

目前为止，应用分布估计算法对极限学习机进行优化的相关研究还较少，因此，本文尝试采用分布估计算法对极限学习机的初始参数进行优化，建立分布估计算法优化极限学习机模型（Estimation of Distribution Algorithm optimizes Extreme Learning Machine，EDA-ELM），应用其对贵州省干旱进行预测，并与在干旱预测当中表现优异的遗传算法优化极限学习机（Genetic Algorithm and Extreme Learning Machine，GA-ELM）模型进行比较分析，研究成果可为贵州省防旱抗旱工作提供技术支撑。

1 研究方法

1.1 极限学习机

Huang等［2］提出的ELM是一种单隐层前馈神经网络算法，学习速度快是这种算法的主要优点。ELM的初始权值与阈值在训练过程中依然是随机生成，根据ELM自身结构特点计算输出权值。

综上，ELM的主要实现过程可归纳如下：选定激励函数g（x）以及隐含层的个数l；随机生成α和d的值；根据规则得到输出权值β。

1.2 分布估计算法优化极限学习机

分布估计算法是一种基于统计学原理的随机进化算法，其进化过程类似于遗传算法却又有本质不同，两者的主要区别可以表述为遗传算法的进化过程是从微观层面进行的，而分布估计算法的进化过程是在宏观方面进行的。遗传算法的进化过程主要包括选择、交叉、变异，而分布估计算法的进化过程没有交叉、变异，而是建立了相应的概率模型对解空间的分布进行描述，进而对种群进行进化选优。变量无关分布估计算法的进化选優过程简述如下［14-15］：

令p（x）=（p（x1），p（x2），…，p（xn））为解空间分布的概率模型的一个概率向量，其中p（xi）（i=1，2，…，n）为第i个基因位置上取1的概率。因此，在算法进化的过程中，每一代的M个个体都是通过概率向量p（x）随机产生的，进而计算每一个个体的适应值，并从中选取最优的N（N<M）个个体来更新概率向量p（x），这里的更新规则采用Heb规则［16］。用pl（x）表示第l代的概率向量，xl1，xl2，…，xlN表示被选择中的N（N<M）个最优个体，则更新过程可以由下式表示：

pl+1（x）=（1－α）pl（x）+α1N∑Nk=1xklX1，…，Xn（6）

式中：α为学习速率。本文中分布估计算法优化极限学习机的初始权值及阈值的主要步骤如下：① 确定ELM的输入与输出样本集；② 采用二进制编码确定对ELM的初始权值及阈值的编码方式；③ 采用高斯概率模型确定解空间的概率模型；④ 采用蒙特卡洛方法确定随机采样产生下一代种群的方式；⑤ 选择升序排列计算每个个体的适应值，并排序选优；⑥ 更新产生下一代种群；⑦ 直至满足终止条件为止。EDA-ELM算法流程见图1。

2 研究区域概况

地处中国西南地区的贵州无平原地形，属亚热带湿润季风气候，地势西高东低，平均海拔达1 100 m。多年平均降水量为1 160.6 mm，但年内分布不均，降水多集中于5～10月，占全年降水的80%左右，常年的相对湿度达70%以上。进入21世纪以来，贵州省的干旱发生频率显著增加，2005～2006年、2009～2010年及2012～2013年均发生了不同程度的干旱，特别是2009～2010年发生的秋冬春三季连旱，给当地的经济社会带来了巨大损失，因此，对贵州省开展干旱预测研究对于当地的抗旱减灾工作有着重要的现实意义。

3 数据来源

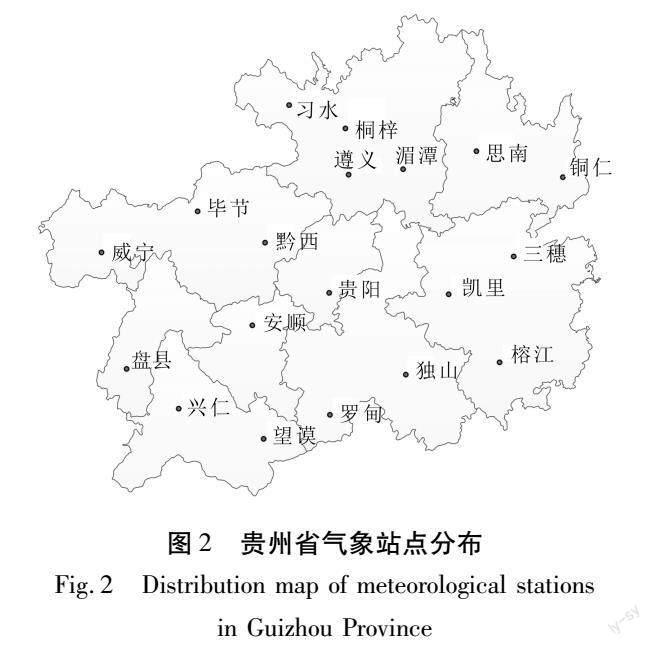
本文数据来源于中国气象数据共享服务网（http：∥data.cma.cn/）1970～2020年贵州省19个气象站点的逐月降水与气温数据。在数据发布之前，国家气候中心已经对数据进行了一致性检验，能够充分保证数据的质量，气象站信息如图2所示。1951～2020年的26项海温指数（Sea surface temperature index，SST）数据（表1）收集自中国气象局国家气候中心网站（https：∥cmdp.ncc-cma.net）。

4 模型计算

4.1 干旱指数计算及数据处理

大量研究表明多因素的干旱指数对干旱评价更为准确［17-19］，因此，本文采用能够同时反映降水与气温对干旱产生影响的标准化降水蒸发指数（Standardized Precipitation Evapotranspiration Index，SPEI）对贵州省干旱情势进行表征，SPEI的计算过程详见文献［18］。研究发现1901～2009年期间，西南地区发生12个月尺度的干旱事件共有33次，且年尺度干旱指数比季尺度和月尺度干旱指数更能准确反映降水和气温的累积效应对干旱的长期影响［20-21］。为此，本文基于12个月尺度标准化降水蒸发指数（SPEI-12）开展了贵州省的干旱预测研究工作，SPEI指数的干旱划分等级详见文献［22］。

为了检验SPEI-12在贵州省干旱评价的适用性，以水利部发布的《中国水旱灾害公报》与国家气候中心发布的中国旱涝监测数据为依据，对SPEI-12的干旱评价准确性与可靠性进行了分析，如表2所示。结果表明：基于SPEI-12的干旱评价结果与实际旱情基本相符，不但干旱历时反映准确，而且干旱强度也判定合理，说明SPEI-12是评价研究区干旱情势的有效指数。

4.2 模型输入因子筛选

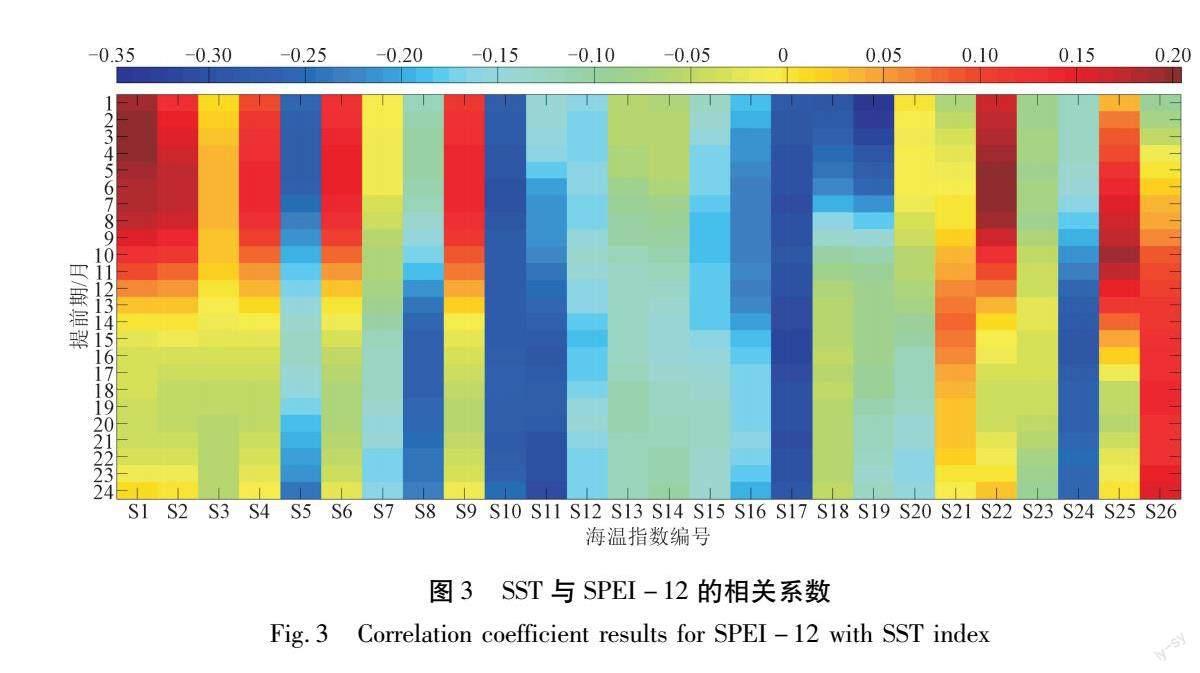
高质量的模型输入是提高干旱预测精度的关键［23］。曾小凡等［24］指出由于大尺度海陆系统的相互作用，导致海温、气压、大气环流指数等与流域径流等水文要素存在遥相关关系，这些遥相关气候因素非常适合作为中长期预报因子。同时，长期的预测实践证明了作为简化描述复杂环流场与天气系统的环流指数是一类可靠的水文预测前兆指示变量［25］。Nguyen等［21］运用SST作为模型输入，成功地对越南盖河流域的干旱进行了预测。因此，本文采用相关分析法对26项SST 与SPEI-12进行普遍相关性筛查，遴选出与SPEI-12间相关系数最大的SST作为模型输入。SST与SPEI-12之间的相关系数矩阵如图3所示。

由于1970～2020年的SST及SPEI-12的数据数目均大于500，所以，当显著性水平为0.001时，查表得到相关系数检验临界值为0.159。这表明大多数的SST与SPEI-12的相关性通过了显著性水平为0.001的检验。为了保证模型运行效率、简化模型输入，以相关系数小于-0.35或者大于0.35为标准，遴选了最终的模型输入变量，即S1715，S1716，S1717，S191，S192，S193，其中下标代表提前期。为了研究不同输入方案对预测精度的影响，基于相关系数由大到小的原则，分别设计了3种不同的输入方案，具体见表3。

4.3 结果分析

由于模型预测训练期一般要求至少30 a以上，故令1970～2012年为模型训练期，2013～2020年為模型测试期。采用均方根误差（Root Mean Square Error，RMSE）和相关系数（Correlation Coefficient，CORR）对预测结果进行评价，具体公式可参见文献［1］。根据ELM，GA-ELM及EDA-ELM原理，应用Python软件进行编程。

EDA-ELM与GA-ELM模型的参数设置主要包括两部分：① 神经网络ELM的参数设置；② 智能算法EDA与GA的参数设置。其中，ELM的隐含层神经元数目设置问题对预测结果的影响尤为显著。目前，通常采用“试错”分析，本文对每一个方案按照隐含层神经元数目从1到100进行了反复试错计算，依次记录评价指标RMSE与CORR的值，最终综合考虑确定ELM的隐含层神经元数目为40。

为了客观比较不同干旱模型的预测效果，EDA-ELM与GA-ELM模型的其他主要参数设置如下：‘sig’为激励函数；GA算法的参数设置为种群大小40，交叉概率为0.7，变异概率为0.01，代沟为0.9，最大进化代数为10 000；EDA算法的参数设置为种群大小40，学习率为0.01，最大进化代数为10 000。考虑到模型运行的随机性，故3种模型分别运行5次，然后求得平均的RMSE及CORR来评价预测性能。

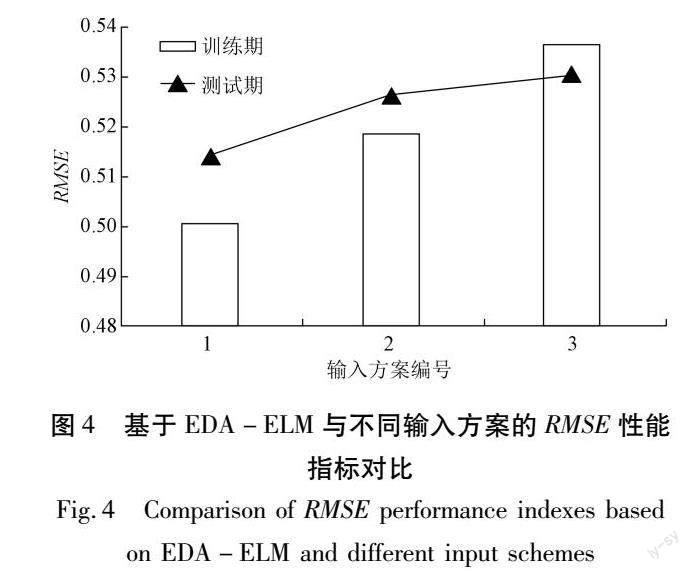
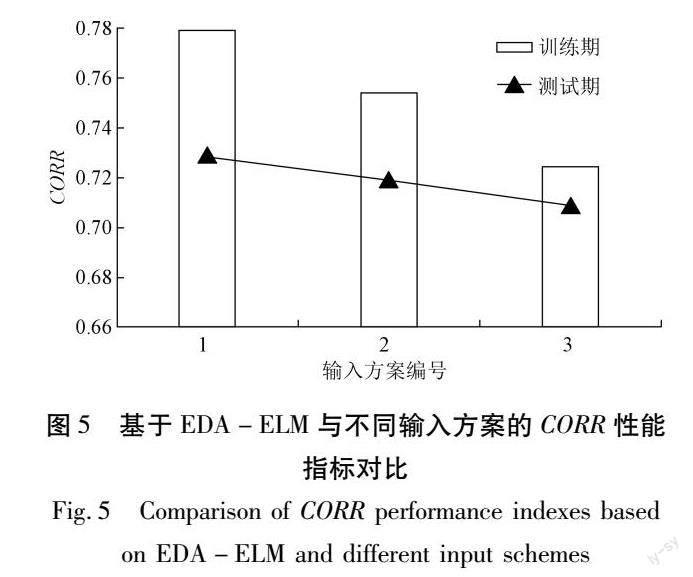
鉴于文章篇幅有限，仅给出了运用新建模型EDA-ELM结合3种不同输入方案对干旱进行预测的效果对比情况，如图4与图5所示。不同输入方案会对干旱预测结果产生一定的影响，具体表现如下：不论是训练期还是测试期，EDA-ELM模型采用输入方案1时干旱预测精度最高，其次是模型采用输入方案2，而模型采用输入方案3时预测精度相对较差，说明同模型条件下干旱预测精度与输入方案关系密切。在有效预测变量组成的输入方案中，输入方案提供的信息量越大，则预测精度越高。同时发现，指标RMSE与CORR在训练期与测试期间的变化态势一致，即RMSE（CORR）随着输入方案由1至3而逐步变大（变小），表明EDA-ELM模型具备良好的泛化能力［26］。

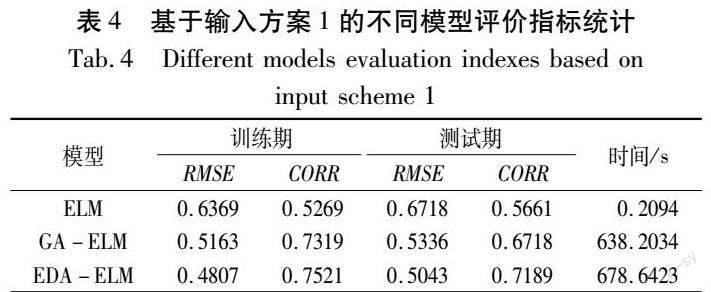
基于最优的输入方案1对比分析了ELM，EDA-ELM与GA-ELM模型在干旱预测时存在的性能差异（表4）。由表4可知，训练期间GA-ELM的RMSE与CORR较ELM分别提高了19.0%与18.7%，EDA-ELM的RMSE与CORR较GA-ELM分别提高了5.5%与7.0%，表明经智能算法调试、优化后的模型预测性能有了大幅度的提升，且同等

条件下分布估计算法优化参数的能力优于遗传算法。同时发现，EDA-ELM与GA-ELM模型的耗时远高于ELM模型，说明智能算法调参、优化模型结构占用了较多时间，EDA算法的进化选优主要依赖种群整体特征，需搭建相应的概率模型，而GA算法的进化选优更加注重种群个体特征、无需构建类似的总体分布模型，因此，EDA算法的耗时又高于GA算法。鉴于干旱预测的实际情况，两种算法的耗时均在可接受的范围之内。为了直观反映不同模型的预测效果，图6给出了不同模型预测干旱的最佳结果对比图。EDA-ELM模型的预测结果与实测值的变化趋势更加接近，能够更好地展现干旱未来发展态势，相较之下，更应该被优先推荐使用。

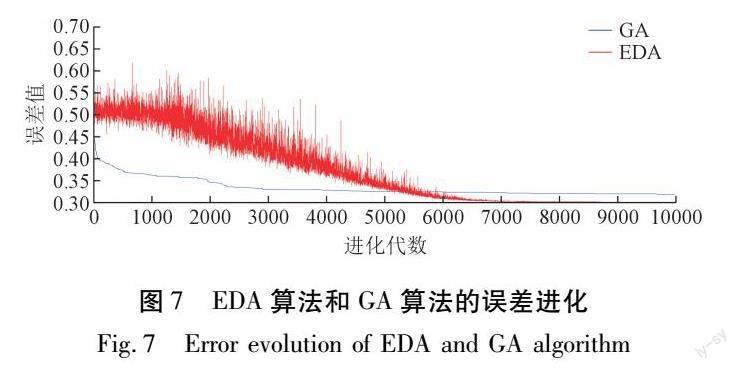
图7为EDA算法与GA算法的进化过程。可以看出，GA收敛始于200代，而EDA收敛始于5 000代，但自进化到5 400代后，EDA的收敛效果开始优于GA。原因是GA有较强的深度搜索能力，所以收敛速度较快，但容易陷入局部最优陷阱；而EDA的广度搜索能力更强，因此收敛速度较慢，但是收敛之后的全局寻优能力更加突出，从而使EDA-ELM模型的预测精度更高。

5 讨论与结论

由于贵州省地貌特征多变、局地气候环境复杂，致使其干旱机理研究难度呈指数级增加。为此，本文借鉴大数据技术研究手段，收集了长系列海温指数数据，计算了其与SPEI指数间的相关性，并遴選了适宜作为干旱预测的关键海温指数，同时构建了分布估计算法优化极限学习机预测模型，较好地完成了研究区的干旱预测任务，进一步提高了干旱预测精度，研究成果可为贵州省气象干旱监测提供技术参考。得到结论如下：

（1） SPEI的干旱评价结果与实际旱情基本相符，不但干旱历时反映准确，而且干旱强度也判定合理，说明SPEI是评价研究区干旱情势的有效指数。

（2） SST是贵州省干旱的有效预测变量，且具有较好的前兆指示作用，如S17的前兆指示期长达15个月，可考虑作为其他地区干旱预测候选因子。

（3） 相同条件下，不同模型的干旱预测精度由高到低依次为EDA-ELM，GA-ELM与ELM，因此，EDA-ELM更适合作为贵州省的干旱预测模型。

研究还有不足：首先，通过数据筛查证实了海温指数与SPEI之间存在良好的相关性，且作为模型输入能够有效对气象干旱进行预测，但海温指数与贵州气象干旱间的响应机理尚不明晰，后续可从气候学的角度展开系统研究工作，从而提高基于数据驱动预测模型的可解释性。其次，EDA具备较强的广度搜索能力，因此随着进化代数的增加，该算法的优化效果随之提高，而GA拥有较强的深度搜索能力，因此该算法的收敛速度更快，下一步可以结合两种算法的优点，开展进一步的深入研究。

参考文献：

［1］ 周靖楠，刘振男.基于自适应差分进化算法优化极限学习机的干旱预测方法［J］.水电能源科学，2018，36（6）：12-15.

［2］ HUANG G B，ZHU Q Y，SIEW C K.Extreme learning machine：theory and applications［J］.Neurocomputing，2006，70（1）：489-501.

［3］ 陈晓青，陆慧娟，郑文斌，等.自适应混沌粒子群算法对极限学习机参数的优化［J］.计算机应用，2016，36（11）：3123-3126.

［4］ HAN F，YAO H F，LING Q H.An improved extreme learning machine based on particle swarm optimization［C］∥International Conference on Intelligent Computing.Heidelberg：Springer，2011：699-704.

［5］ 王杰，毕浩洋.一种基于粒子群优化的极限学习机［J］.郑州大学学报（理学版），2013，45（1）：100-104.

［6］ ZONG W，HUANG G B，CHEN Y.Weighted extreme learning machine for imbalance learning［J］.Neurocomputing，2013，101：229-242.

［7］ LIU X，WANG L，HUANG G B，et al.Multiple kernel extreme learning machine［J］.Neurocomputing，2015，149：253-264.

［8］ 王杰，郭晨龙.小波核极限学习机分类器［J］.微电子学与计算机，2013，30（10）：73-76.

［9］ 王杰，苌群康，彭金柱.极限学习机优化及其拟合性分析［J］.郑州大学学报（工学版），2016，37（2）：20-24.

［10］ 周华平，袁月.改进鱼群算法优化的ELM在乳腺肿瘤辅助诊断中的应用研究［J］.计算机工程与科学，2017，39（11）：2145-2152.

［11］ 吕忠，周强，周琨，等.基于遗传算法改进极限学习机的变压器故障诊断［J］.高压电器，2015，51（8）：49-53.

［12］ CAO J，LIN Z，HUANG G B.Self-adaptive evolutionary extreme learning machine［J］.Neural Processing Letters，2012，36（3）：285-305.

［13］ 刘振男，杜尧，韩幸烨，等.基于遗传算法优化极限学习机模型的干旱预测——以云贵高原为例［J］.人民长江，2020，51（8）：13-18.

［14］ BALUJA S.Population-based incremental learning.a method for integrating genetic search based function optimization and competitive learning［R］.Pittsburgh：Carnegie Mellon University，1994.

［15］ BALUJA S.An Empirical Comparison of Seven Iterative and Evolutionary Function Optimization Heuristics［R］.Pittsburgh：Carnegie Mellon University，1995.

［16］ YEH I C.Modeling of strength of high-performance concrete using artificial neural networks［J］.Cement and Concrete Research，1998，28（12）：1797-1808.

［17］ 劉小龙，虞美秀.中国近60年干旱演变特征分析［J］.干旱区资源与环境，2015，29（12）：177-183.

［18］ 熊光洁，张博凯，李崇银，等.基于SPEI的中国西南地区1961-2012年干旱变化特征分析［J］.气候变化研究进展，2013，9（3）：192-198.

［19］ 王文，黄瑾，崔巍.云贵高原区干旱遥感监测中各干旱指数的应用对比［J］.农业工程学报，2018，34（19）：131-139.

［20］ 王林，陈文.近百年西南地区干旱的多时间尺度演变特征［J］.气象科技进展，2012，2（4）：21-26.

［21］ NGUYEN L B，LI Q F，NGOC T A，et al.Adaptive Neuro-Fuzzy inference system for drought forecasting in the Cai River Basin in Vietnam［J］.Journal of the Faculty of Agriculture Kyushu University，2015，60（2）：405-415.

［22］ BACANLI U G，FIRAT M，DIKBAS F.Adaptive Neuro-Fuzzy Inference System for drought forecasting［J］.Stochastic Environmental Research and Risk Assessment，2009，23（8）：1143-1154.

［23］ 赵铜铁钢，杨大文.神经网络径流预报模型中基于互信息的预报因子选择方法［J］.水力发电学报，2011，30（1）：24-30.

［24］ 曾小凡，周建中.长江流域年平均径流对气候变化的响应及预估［J］.人民长江，2010，41（12）：80-83.

［25］ 王世杰，刘柯莹，孟长青.基于SPEI的嘉陵江流域旱涝时空演变分析［J］.水利水电快报，2022，43（5）：12-19.

［26］ 魏海坤，徐嗣鑫，宋文忠.神经网络的泛化理论和泛化方法［J］.自动化学报，2001（6）：806-815.

（编辑：江 文）