基于减振性能的市域铁路弹性支承块轨道刚度匹配研究*

2023-08-28赵坪锐章元爱

城市轨道交通研究 2023年8期

谢甜赵坪锐章元爱

(1.西南交通大学土木工程学院,610036,成都; 2.中铁西南科学研究院有限公司,610036,成都∥第一作者,硕士研究生)

为降低振动对周边环境的影响,从轮轨振动的源头采取措施是较为有效的一种措施,如在轨道系统的扣件、轨枕或道床等位置采取减振措施等[1]。

轨道结构参数对轨道振动频域分布的影响具有明显的差异,可根据激振频率的分布特性以及减振参数对频率的敏感特性进行减振参数的合理匹配,以达到较好的减振效果[2]。本文建立车辆-轨道耦合动力学计算模型进行动力学仿真计算,研究不同扣件垂向刚度及弹性支承块垂向刚度组合下弹性支承块轨道结构的振动响应,进而确定弹性支承块轨道结构中轨下刚度(即扣件垂向刚度)和块下刚度的合理取值。

1 车辆-轨道耦合模型

车辆-轨道耦合模型是一种多刚体和柔性轨道相互作用的刚柔耦合模型。

市域铁路多采用CRH6型动车组。该动车组为8节编组,具有载客量大、列车起停频率髙及快速乘降能力强等特点,可在城际线路和既有客运专线上运行[3]。在车辆-轨道耦合模型中,CRH6型动车组的动力学参数如表1所示[3-4]。

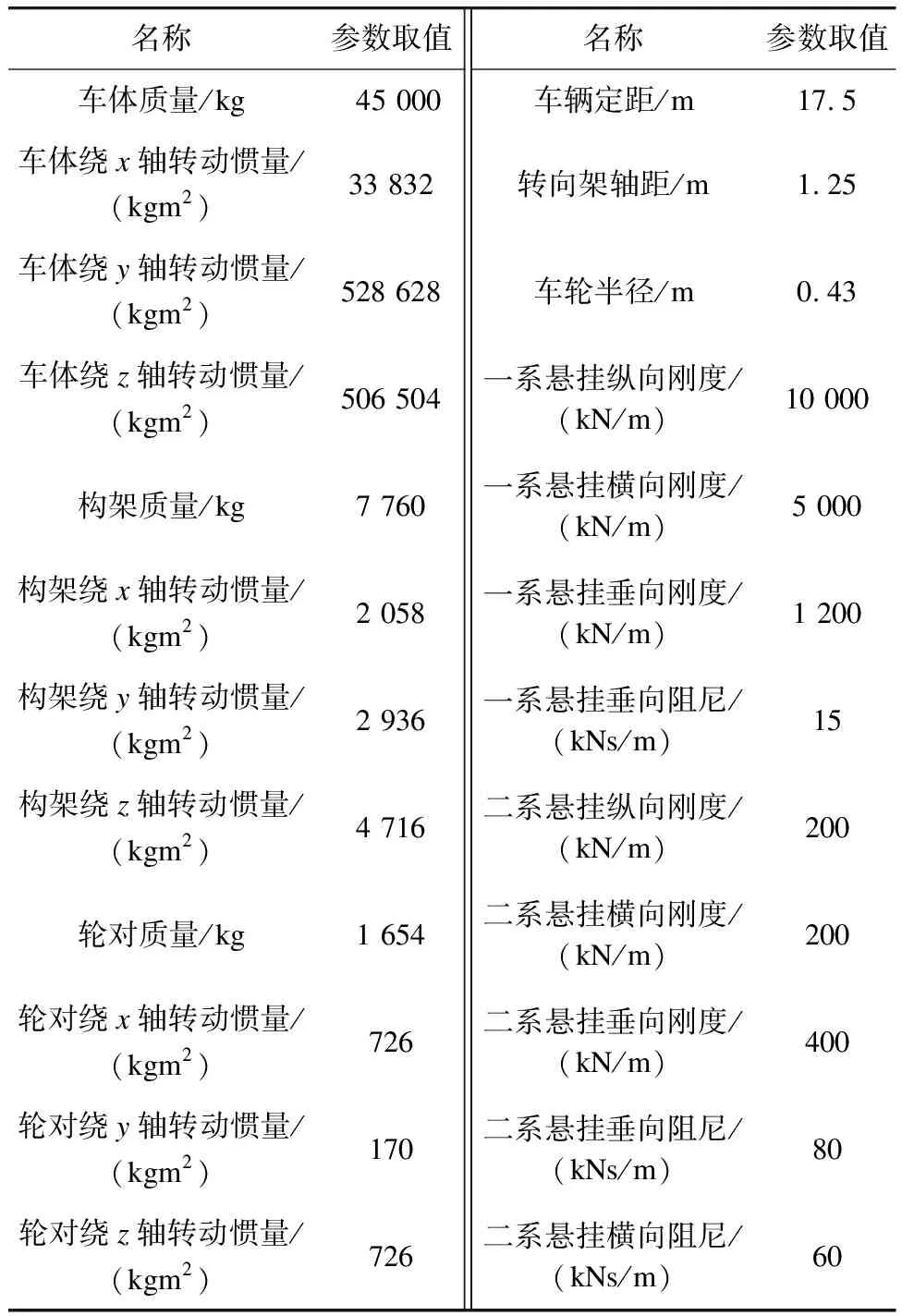
表1 CRH6型动车组的动力学参数

弹性支承块式轨道由钢轨、扣件、轨枕和枕下基础构成。在车辆-轨道耦合模型中:钢轨被视为铁木辛柯梁;扣件采用Bushing力元模拟;单个支承块可视为一个刚体,具有4个自由度;采用弹簧阻尼元件连接轨枕和道床板;道床板为弹性薄板[5];利用弹簧阻尼元件实现弹性支承块与下部基础的连接。车辆-轨道耦合模型见图1。

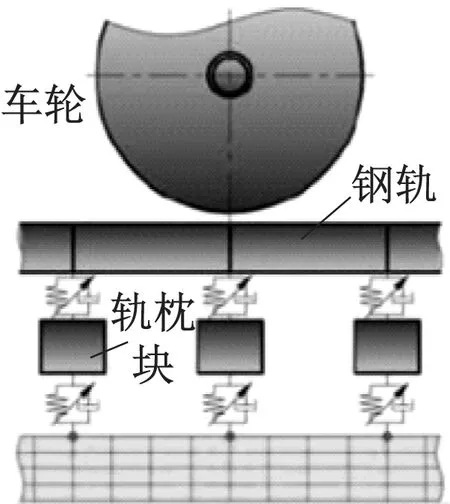
a) 模型纵向图

车辆-轨道耦合模型中,钢轨型号为CHN60N,道床板采用C40混凝土。弹性支承块轨道各部件的结构参数如表2所示。

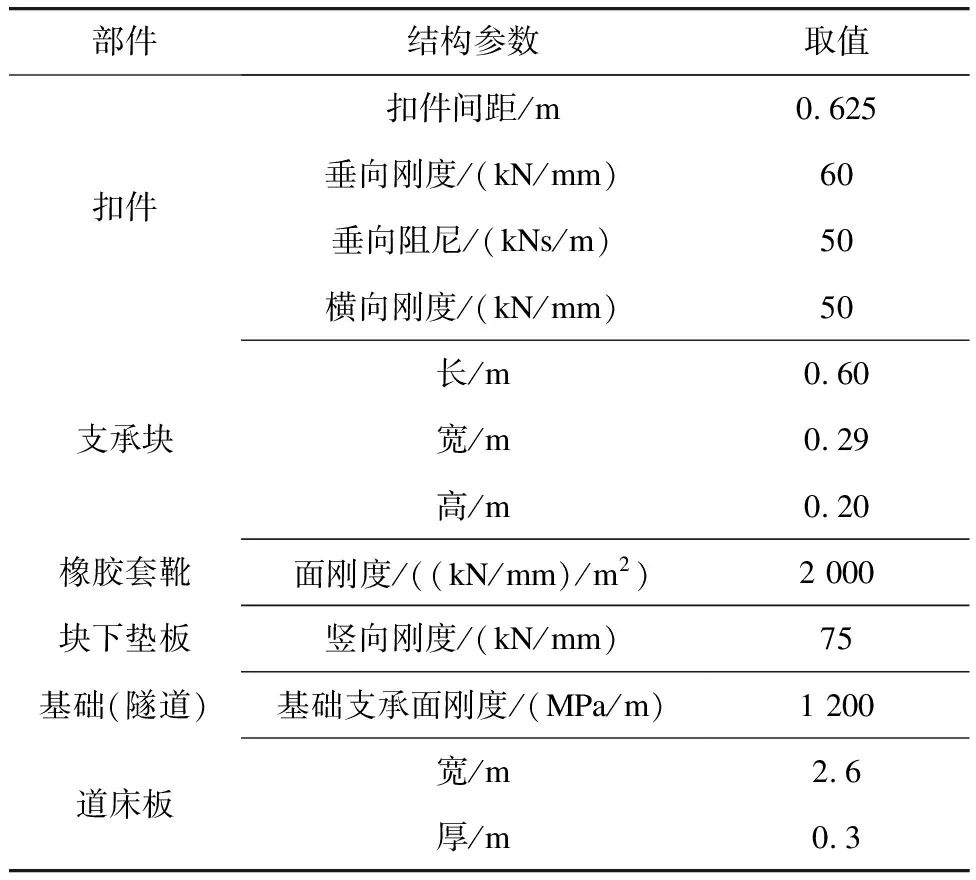
表2 弹性支承块轨道各部件的结构参数取值

在车辆-轨道耦合模型中,车辆与下部轨道结构的相互作用通过轮轨间的耦合关系实现,其中轮轨接触采用传统的Hertz非线性弹性接触模型来模拟。

在UM(多体动力学)仿真软件中,准确设置轮轨之间的相互作用关系,选择美国六级轨道谱作为轨道不平顺谱输入,选择Park求解方法,即可进行弹性支承块轨道减振的计算。车辆-轨道仿真模型如图2所示。

图2 车辆-轨道仿真模型

2 数据处理和评价方法

对振动进行评价时,由于振动有效值的变化范围通常高达数百万倍,这给振动描述带来不便,于是引入了振动级(或称振动水平)的概念来替代有效值描述振动大小,对于不同的物理量,振动级可以为加速度级、速度级和位移级[6]。本文采用Z振级进行评价。

评价环境振动的物理量是加速度振级LVA,单位为dB,其计算式为:

式中:

a——垂向振动加速度值;

a0——基准加速度值,取10-6m/s2。

将LVA按 ISO 2361/1:1997《机械振动与冲击人体处于全身振动的评价第1部分》中规定的全身振动Z计权因子修正后即得到垂向振动加速度级(以下简称“Z振级”),记作LV,单位为dB。

3 时域评价

图3为列车分别通过弹性支承块轨道道床段和无减振的普通整体道床段时,钢轨和道床板的垂向振动加速度时域图。由图3可见,对于同一测点的时域加速度值,两种道床(弹性支承块轨道道床和普通整体道床)的变化趋势基本相同,在时域内不能对振动结果准确评价[7],因此要从频域角度对刚度匹配进行分析。

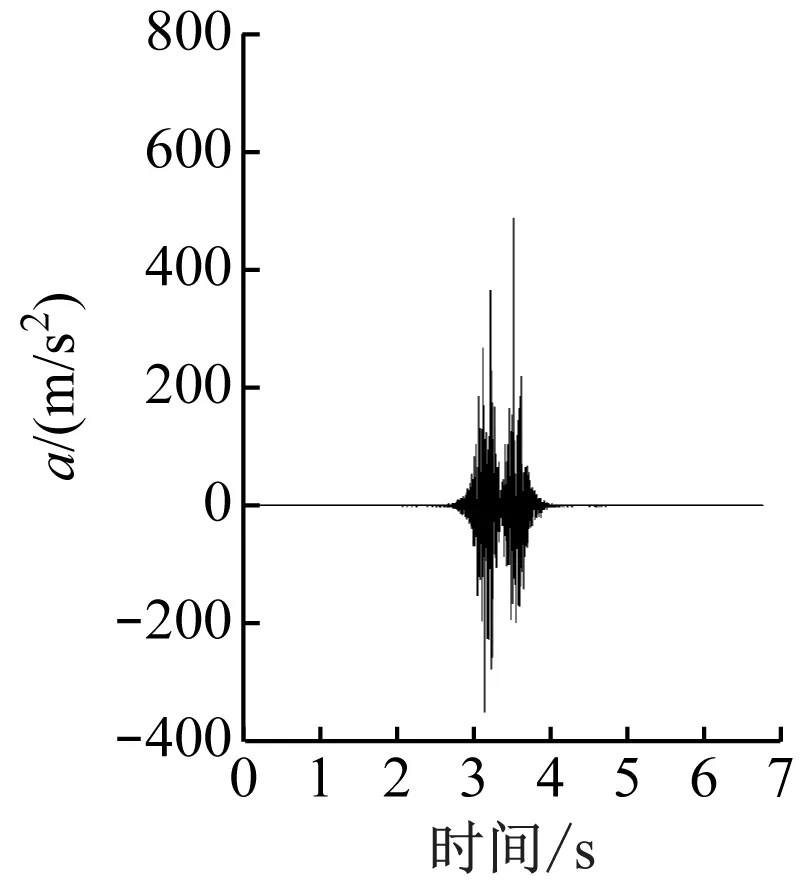
a) 弹性支承块轨道钢轨

4 刚度匹配分析

在不同轨下刚度和块下刚度组合情况下,由车辆-轨道耦合模型仿真得到弹性支承块轨道道床和整体道床的道床板动力响应;对加速度时程进行傅里叶变换[8],可得到两种道床的频响曲线;对振动加速度的时域数据进行1/3倍频程计算,可得到两种道床的分频振级曲线。

4.1 轨下刚度

保持其他参数不变,改变轨下刚度分析系统各项动力响应。轨下刚度分析范围为60～120 kN/mm,块下胶垫刚度为50 kN/mm,两种道床的分频振级曲线如图4所示。

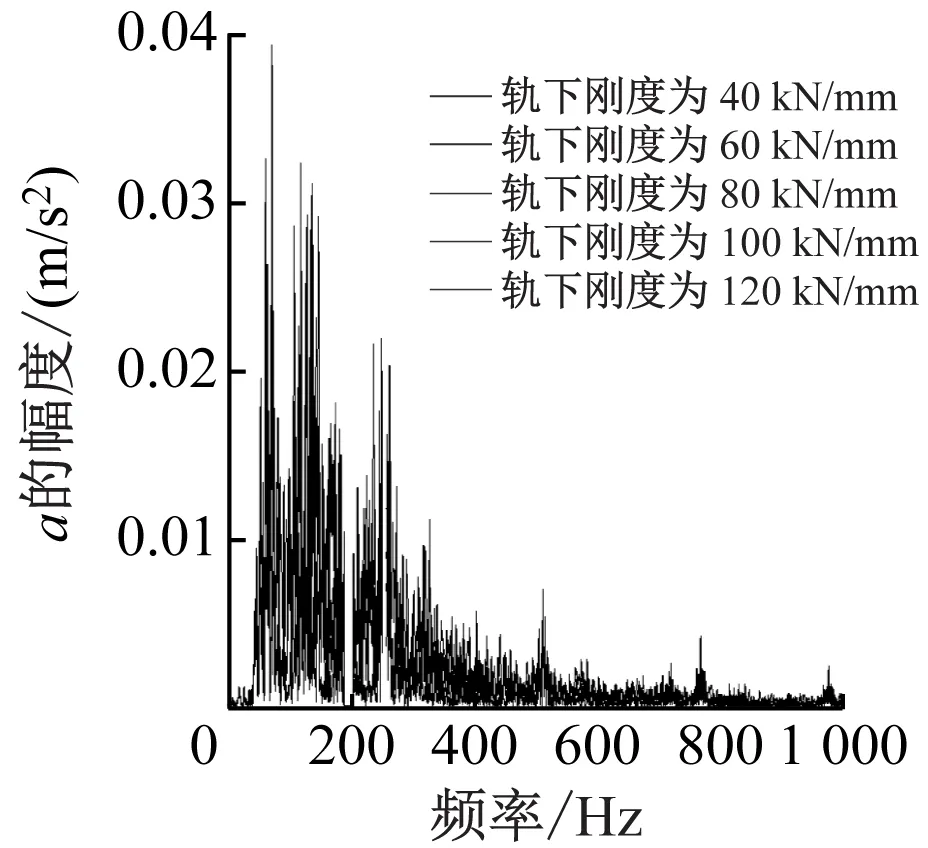
a) 弹性支承块道床板频响曲线

由图4可见:弹性支承块道床板的振动响应主要集中在0～300 Hz范围内;轨下刚度对道床板的振动响应在频域上的分布基本没有影响;道床板振动响应的峰值主要集中在中心频率为50～60 Hz及115～125 Hz范围内,其Z振级最大值为80.53 dB。

整体道床振动响应同样主要集中在0～300 Hz范围内,但轨下刚度对整体道床振动的峰值频率有较大影响,轨下刚度取40 kN/mm时,Z振级峰值主要集中在中心频率250～255 Hz范围内,最大值为81.31 dB,轨下刚度取60、80 kN/mm时,振动响应峰值主要集中在中心频率135～145 Hz范围内,最大值分别为82.83、86.52 dB;扣件垂向刚度为100、120 kN/mm时,Z振级峰值主要集中在中心频率65～70 Hz范围内,最大值分别为87.31、87.5 dB。

4.2 块下刚度分析

保持轨下刚度80 kN/mm不变,块下刚度分别取50、80、110、140及170 kN/mm时,两种道床的分频振级曲线如图5所示。

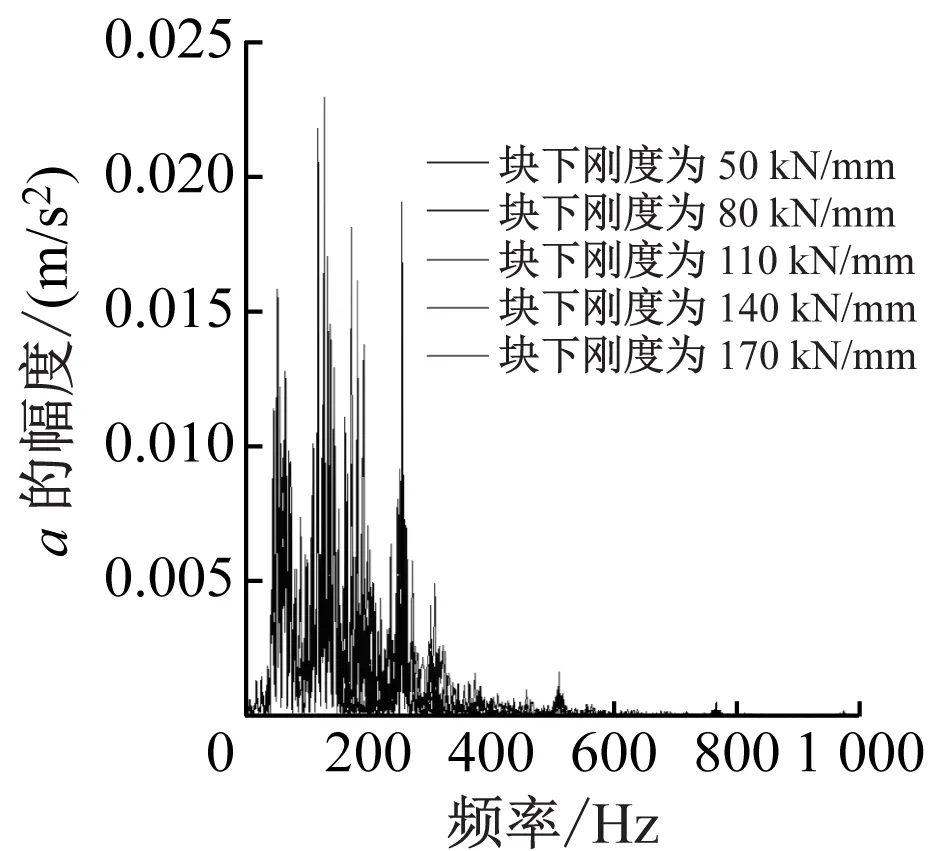
a) 弹性支承块道床板频响曲线

由图5可见,保持轨下刚度80 kN/mm不变,块下刚度分别取50、80及110 kN/mm时,道床板Z振级的峰值主要集中在中心频率为55～65 Hz及115～125 Hz的范围内,其Z振级最大值分别为78.52、79.03及79.31 dB。块下刚度取140、170 kN/mm时,道床板Z振级的峰值主要集中在中心频率为120～125 Hz的范围内,其Z振级最大值分别为82.0、82.5 dB。

4.3 Z振级

对不同轨下刚度和块下刚度下两种道床的1/3倍频程计算数据,乘以中心频率对应的全身振动Z计权因子,计算得到弹性支承块轨道板和普通整体道床的Z振级[9],如表3所示。

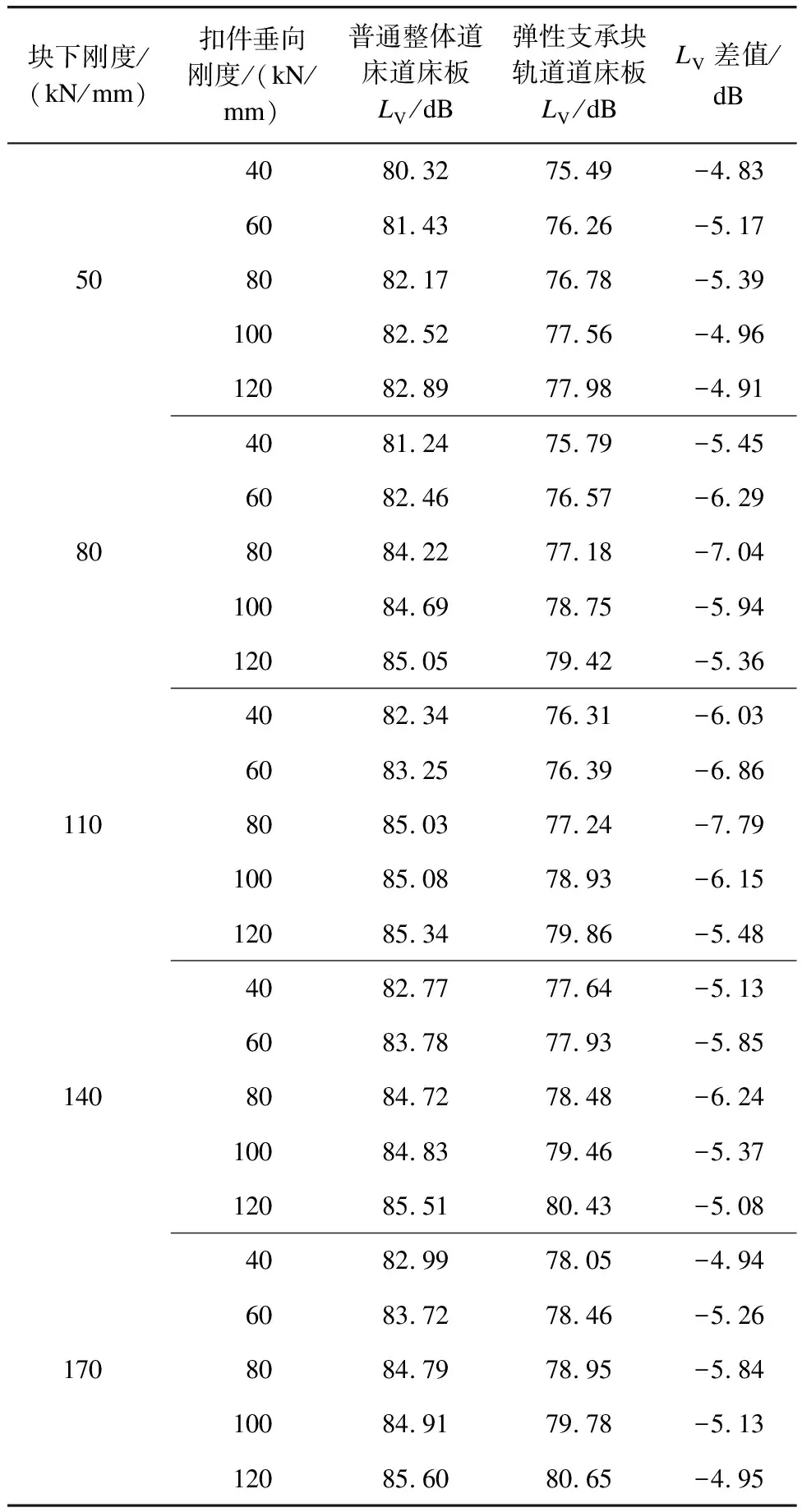
表3 弹性支承块轨道板和普通整体道床Z振级

由表3可知,块下刚度增大时,弹性支承块轨道道床板的Z振级随之增大;轨下刚度增大时,弹性支承块轨道道床板的Z振级随之增大,普通整体道床的Z振级也略有增大。由表3还可以看出,块下刚度为80～110 kN/mm时,弹性支承块轨道道床板和普通整体道床的振级差比较大,最大为7.79 dB,说明列车荷载作用下的振动响应从弹性支承块轨道传递到刚性基础的过程衰减较大,减振效果较好。轨下刚度从40～120 kN/mm范围内变化时,振级差从小到大再到小变化,轨下刚度在60～80 kN/mm时振级差较大,说明在此范围内减振效果比较好。