变截面三维机翼的气动性能及噪声研究

曹开强

（200093 上海市 上海理工大学 机械工程学院）

0 引言

机翼绕流的现象属于三维的湍流流动，并且是绕流现象中十分常见的问题。对于机翼绕流的研究不仅可用于航空航天业，而且可为风力机以及水利行业提供借鉴。研究机翼绕流对于提高翼型元件的气动性能、降低气动噪声等方面具有十分重要的意义。随着近些年来翼型元件的绕流速度越来越快、计算机技术水平的不断提高，其相关的数值研究也越来越被重视。对于翼型绕流的研究不仅局限于翼型的气动性能，也更多地关注到翼型的气动噪声方面。计算气动噪声的方法目前比较通用的是使用基于Lighthill 声类比模型[1]的Ffowcs Williams-Hawkings 方程[2]（FW-H 方程）。

大涡模拟作为CFD 中兼具精度性和经济性的数值模拟方案，在近些年来得到了广泛的应用和发展。2015 年，樊艳红[3]使用基于WALL 亚格子模型的大涡模拟方法对风力机翼型绕流进行数值模拟，并把模拟结果和实验结果进行对比，发现模拟结果能很好地吻合实验结果，说明使用WALL 亚格子模型的大涡模拟能准确模拟翼型绕流。本文使用ANSYS Fluent，采用基于WALL 亚格子模型[4]的大涡模拟（LES）方法对三维变截面机翼的气动特性机翼气动噪声进行数值模拟研究，旨在为三维变截面机翼绕流方向上的气动性能研究提供一些参考，使对于翼型气动特性和气动噪声的产生机理及现象做进一步的了解和认识。

1 数值模拟方法

1.1 湍流数值模拟方法

LES 是目前适用非常广泛的一种流场数值模拟方法，能根据网格的精密度而自由地调整数值模拟的精度。其相比于直接数值模拟（DNS）需要的网格分辨率和计算量都更少，能节约大量的计算资源，同时又能够获得比雷诺时均模拟（RANS）方法更多的湍流信息，例如大尺度涡流的速度和压强脉动等。因此LES 是结合目前计算机能力下非常具有应用价值的数值模拟方法，也是CFD 的一个热门领域。

LES 的基本思想是根据网格尺度把湍流分为大尺度湍流和小尺度湍流[5]，对大尺度的湍流直接使用N-S 方程进行求解计算。而小尺度的湍流因为其具有各向同性，并且小涡对大涡的影响在运动方程中体现为类似于雷诺应力的应力项，称之为亚格子雷诺应力，所以在LES 中利用了亚格子模型模拟小涡对大涡的影响，而不直接求解小尺度涡，以此节省大量计算，使求解变得可能。假设在流场中某瞬态变量为φ（x，t），对该变量采用滤波操作，如式（1）、式（2）[6]：

经过这个滤波操作后，瞬态变量φ（x，t）被分解为2 部分：，其中代表大尺度的变量，φ'（x，t）代表小尺度的变量。

本文使用ANSYS 软件，采用三维、不可压缩的非定常模拟方法进行仿真计算，控制方程的离散方法是有限体积法[7]。使用大涡模拟方法求解流场信息，LES 亚格子模型采用WALL 模型[4]，WALL的优点在于黏性系数不随计算网格而改变，也不受周围湍流情况的影响，目前已经得到越来越多的应用。速度和压力耦合方案选用SIMPLEC[8]，空间离散格式为2 阶中心差分格式，时间项离散格式为2 阶隐式计算格式。

1.2 FW-H 方程

气动噪声的产生和传播可直接通过求解N-S 方程得到，但是这就要求计算所使用的网格必须具有很高的精度，这意味着计算量大、耗时长。为了弥补这些缺点，在Fluent 里采用基于Lighthill 声学近似模型的FW-H 方程，该方法可将声音的产生和传播过程分开计算，相比直接求解N-S 方程减少了工作量，对计算机的要求也降低，使求解变得可能。

FW-H 方程是Ffowcs Williiams 和Hawkings 在1969 年引入广义函数根据N-S 方程推导出来的，在静止流体中运动物体发声的控制方程，表示为

在计算时，需要用到的流场变量通常包括速度分量、压强分布等信息，这些信息可以使用LES或者DES 等方法获得。在本文中使用LES 方法求解流场信息，结合FW-H方程求解流动的声场信息，设置机翼表面为声源面。

2 模型建立和网格划分

2.1 模型建立

本文是基于NACA 0018 对称翼型建立的三维变截面机翼模型，其中大弦长C1=100 mm，小弦长C2=95 mm，展向长度20 mm，建立模型如图1 所示。

图1 变截面三维机翼Fig.1 Variable section 3D wing

流体域建立时，将机翼的左右两侧面与流场模型的耦合边界完全贴合，即流体域的宽度等于翼型展向长度为20 mm。以机翼前缘点作为参考，流体域入口到前缘参考点的距离L1=200 mm，流体域进口设置为速度入口条件。流体域出口到前缘参考点的距离L2=400 mm，流体域上边界到前缘参考点的距离H1和流体域下边界到前缘参考点的距离H2均为130 mm，可认为上下壁面对翼型附近的流动不产生影响。机翼前缘参考点距流场出口的距离要大于距流场入口的距离，以消除可能存在的回流对于流场计算的影响。设置机翼的迎角为15 °。流体域模型的建立如图2 所示。

图2 三维流体域示意图Fig.2 Schematic diagram of 3D fluid domain

2.2 网格划分

网格划分必须根据所使用的湍流数值模拟方法进行，因为不同的湍流数值模拟方法对网格和边界层的要求不同。LES 对网格要求足够精细，网格分辨率要能满足计算所需捕捉的最小湍流的尺度。在LES 中，大于网格尺度的湍流将被直接求解，而小于网格尺度的湍流将使用亚格子模型表征其对大涡的影响，所以网格尺度体现了LES的计算精度。

不同的数值模拟方法对于边界层的要求也是不一样的，总体而言，边界层的处理方法包括壁面函数法和近壁面模型，本文LES 要求使用近壁面模型法。不同的边界层处理方法要求不同的y+值标准，y+作为边界层网格划分的衡量依据，其值直接和边界层的第1 层网格高度相关，是一个无量纲数，表达式为

式中：u*——近壁面摩擦速度；y——第1 层网格距离壁面的距离；ν——流体的运动粘度。

壁面函数法和近壁面模型对y+的要求是不同的，近壁面模型方法要求在近壁面内要分布足够细密的网格，通常要求y+在1 左右。

根据式（2），可大致推算出本文模型所需要的第1 层网格高度为0.013 mm，边界层设置15 层，增长率为1.2，能满足本文LES 的y+要求。其它网格尺度为1 mm，网格总数为460 万，网格质量全部在0.5 以上且大部分都在0.7 及以上，能满足本文模型对于网格的要求。网格划分详情如图3 所示。

图3 网格划分Fig.3 Mesh

3 Fluent 仿真计算

使用Fluent2021 R2 大涡模拟对模型进行瞬态仿真，亚网格尺度模型使用WALE 模型，声学模型使用FW-H 模型。Fluent 求解器类型设置为采用压力修正算法的压力基求解器，压力速度耦合算法使用SIMPLEC,空间离散格式为2 阶中心差分格式，时间项离散格式采用2 阶隐式算法，设置流场速度入口流速为40 m/s。设置时间步长为0.000 01 s，计算时间步数为10 000 步。

机翼模型中尺度最小的网格为边界层加密网格，其流向长度为0.5 mm，而流体流速为40 m/s，流体流过一个网格单元需要0.000 012 5 s，因此本文选取的0.000 01 s 能满足计算要求。机翼模型的大弦长为0.1 m，流体完整流过机翼需要0.002 5 s，即250 个时间步，因此本文计算所采用的时间步数均满足计算要求。求解具体设置如表1 所示。

表1 求解参数及设置Tab.1 Solving parameters and settings

4 非稳态流场

4.1 压力场

图4 给出翼型表面的压力云图、图5 为翼型中间截面的压力分布云图（z=10 mm），结合图4 和图5 可得翼型表面压力分布的大致规律。在上翼面靠近前缘位置处有一个压力的低峰值区，该区域的压力低峰值是气流在此处的高速流动造成的；在翼型下翼面靠近前缘位置处存在压力高峰值区，该压力高峰值区是由于驻点的存在。

图4 翼型表面压力云图Fig.4 Airfoil surface pressure cloud map

图5 截面压力云图Fig.5 Sectional pressure contour

图6 展示的是翼型表面的压力分布曲线，位于上方的曲线是翼型下半部分的压力分布曲线，位于下方的曲线是翼型下半部分的压力分布曲线。图6中压力最大的点就是位于翼型下表面的驻点位置。另外值得注意的是，由图6 可以明显看出翼型下表面的压力分布总体比较平稳，没有产生压力突变的情况，说明下表面的流动状态比较平稳。而翼型上表面的压力则有波动和突变的情况，这说明在翼型上表面产生了流动不稳定性，该流动不稳定性造成的压力波动势必会引发噪声的产生。

图6 翼型表面压力分布曲线Fig.6 Pressure distribution curve of airfoil surface

4.2 速度场

图7 给出了流场的速度分布云图，图7 中的a点和b 点分别对应压力场中的最大压力点和最小压力点。值得注意的是，从图7 可以明显看出翼型下表面的速度分布非常平稳，没有出现速度波动的情况，而翼型上表面则出现了速度波动，和压力场的分布情况类似。进一步说明在翼型的上表面存在流动不稳定。在翼型上表面中部可以看到间断小区域的速度波动区，在翼型尾缘附近出现更大范围的速度波动区，说明在翼型中部可能存在间断的分离泡，并且在翼型尾缘处发展成为更大范围的湍流现象，可以清晰看到尾缘处存在涡的脱落。

图7 速度分布云图Fig.7 Velocity distribution cloud map

图8 给出的是翼型附近的速度矢量图，从A点局部放大图可以看出,在翼型中部有断续的分离泡生成，分离泡在流向位置上不断地形成，这也解释了上文翼型上表面压力和速度的波动现象。B 局部放大图展示了在翼型尾缘存在更剧烈的湍流现象，并且形成了涡流。

图8 速度矢量图Fig.8 Speed vector

4.3 紊流

结合图9 涡量图和图10 涡旋强度图可以看出，流动在翼型的上表面和机翼尾缘附近都形成了涡流。因为机翼存在正迎角，所以机翼上表面存在逆压梯度，造成了机翼上表面发生流动分离以及涡流现象。由于逆压梯度的存在，在翼型上表面靠近前缘附近区域开始形成分离泡并产生流动不稳定性，在翼型上表面中部区域紊流强度并不高，沿着翼型表面向下游紊流强度越来越大。结合之前的速度矢量图可以知道流场最终在尾缘附近形成涡结构，并且从尾部脱落飘向下游，尾涡的脱落也会产生涡脱落噪声[9]。

图9 涡量图Fig.9 Vorticity

图10 涡旋强度Fig.10 Swirling strength

图11 和图12 是机翼表面部分流体的迹线图，这些迹线是流经机翼中间截面的部分流体的运动轨迹。可以很清晰地看到，具有逆压梯度的机翼上表面流动在某个位置之后开始呈现无序状态，并且在机翼的展向位置上具有很大的流动跨度。结合速度矢量图以及压力云图等可以看出，流动开始呈现无序状态的位置就是机翼上表面开始出现分离泡的位置。由于分离泡的出现，导致了流动开始出现不稳定性并且出现强烈的展向流动，使得流体在展向上具有很大的跨度，这种展向的流动进一步加剧了压力和速度的波动。而机翼下表面的流动则十分稳定，没有出现流动不稳定性以及在展向的流动。

图11 机翼上表面迹线图Fig.11 Traces on upper surface of the wing

图12 机翼下表面迹线图Fig.12 Traces on lower surface of the wing

5 声场

图13 是机翼壁面的声源强度分布图，可以明显看到在8 mm 和90～100 mm 这2 个区域存在2 个声源强度峰值区。第1 个峰值区的位置是流体在机翼上的驻点位置，流体理论上是在驻点位置和机翼相遇的，因此该峰值区的产生是由于流体在此处与机翼表面相撞所产生的偶极子噪声。可以看出该噪声占据了很大的声源强度比重。在机翼尾部90～100 mm 之间也有一个声源强度峰值区，该峰值区是由于机翼尾部具有湍流边界层后缘散射噪声和涡脱落噪声。

图13 壁面声源强度分布Fig.13 Intensity distribution of wall sound source

在距离前缘参考点380 mm 处布置一个信号接收点，具体坐标为（380，0，10）。根据LES 计算流场信息，可以得到声压的时间序列，经过FFT变换即可得到噪声的声压频谱图，如图14 所示。从图14 可以明显看出噪声的整体声压级水平维持在70 dB 左右且宽频噪声占主要，这说明后缘的散射噪声占据了重要的比例。

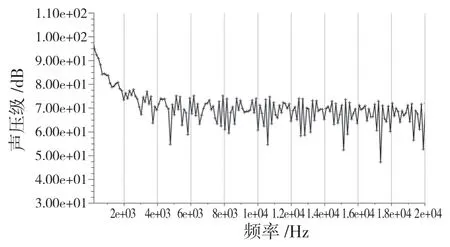
图14 声压级频谱图Fig.14 Sound pressure level spectrogram

6 结论

（1）本文变截面三维机翼在攻角为15°的情况下，上表面和下表面的流动状态具有很大的不同。由于逆压梯度的存在，机翼上表面在中部位置形成间断的分离泡，产生了流动不稳定性并且导致机翼上表面压力和速度的波动。机翼上表面的流动不稳定性在后缘位置得到放大，演变为尺度更大的涡流现象并且伴随后缘的涡脱落。而机翼下表面的流动则十分平稳，没有流动不稳定现象，也没有压力和速度的明显波动。

（2）在本文变截面三维机翼上表面的流体产生流动不稳定性后具有很大的展向跨度，这些流体在机翼展向上的流动会产生展向上的相互影响并且加剧流动不稳定性。在机翼下表面，由于流动比较稳定，所以没有产生展向流动。

（3）机翼驻点位置由于空气和机翼的撞击作用，导致驻点具有很高的声源强度；机翼表面的流动不稳定性造成压力和速度的波动等现象，也会造成机翼表面声源强度的波动。由于机翼尾缘具有湍流边界层后缘散射噪声和涡脱落噪声，因此在机翼尾缘处也具有较高的声源强度。噪声整体呈现宽频的特性，且基本维持在70 dB 左右。