基于改进人工势场法的多目标点路径规划

唐瑞东，游向荣

（430065 湖北省 武汉市 武汉科技大学 汽车与交通工程学院）

0 引言

路径规划在智能小车自主导航技术[1]中是一种关键性技术，传统的路径规划算法分为全局路径规划与局部路径规划。全局路径规划算法有BFS、Dijkstra 算法及A*算法[2]；局部路径算法有人工势场法（APF）、动态窗口法（DWA）。与其它算法比较，人工势场法具有计算量小、避障响应快、便于硬件实现等优势[3]。人工势场法是一种虚拟力法[4]，其基本思想是将机器人在环境中的运动抽象成为一种人造引力场中的运动，目标点对运动中的机器人产生“引力”作用，障碍物对机器人产生“斥力”作用，最后通过求合力来控制移动机器人的运动。应用人工势场法规划的路径一般比较平滑且安全，但是这种方法存在局部最优点问题以及目标点不可达问题，这是本文研究的核心内容。

1 传统的人工势场法及改进算法

1.1 传统的人工势能场算法及其缺陷

人工势场法的原理是机器人在移动过程中障碍物形成虚拟的“斥力”势场，目标物体形成虚拟的“引力”势场，在“引力”与“斥力”势场的共同作用下，物体逐渐避开障碍物的高势能场，到达目标点低势能场。如图1 所示。

图1 人工势场法原理图Fig.1 Schematic diagram of artificial potential field method

1.1.1 引力场

目标点对移动机器人形成的引力势能随着机器人与目标点之间距离的改变而变化，人工势场中引力势能与机器人与目标点之间距离的平方成正比[5]，即距离越远，目标点所产生的引力势能越大。

引力势场函数表示为

式中：Uatt（q）——目标点对机器人产生的引力场；ε——大于0 的引力势场增益函数；ρ（q,qgoal）——机器人当前位置与目标点之间的欧几里得距离。

1.1.2 斥力场

在人工势场中，机器人与障碍物之间的距离越远所受斥力越小，反之越大[6]。

斥力势场函数表示为

式中：Urep（q）——障碍物对机器人当前位置所形成的斥力势场；η——斥力势场增益函数；ρ（q,qobs）——障碍物与机器人当前位置的欧几里得距离；ρ0——障碍物的影响半径，即斥力势场的有效作用距离。当ρ（q,qobs）>ρ0时，障碍物对机器人不再产生斥力作用。

机器人当前所处位置周围有n 个障碍物时，机器人当前所处位置的势能为

传统的人工势能法指机器人在当前位置遍历多个方向，最后寻找势能最小的那个方向并移动一个步长，直至最后到达终点。其原理图如图2 所示。

图2 多障碍物人工势场法原理图Fig.2 Schematic diagram of multi-obstacle artificial potential field method

1.1.3 传统人工势场法存在的缺陷

（1）局部势能极小点问题。当障碍物在移动机器人与目标点之间零散排布时，存在局部势能极小值点问题，导致移动机器人在两点之间振荡。

（2）目标点不可达问题。当目标点周围障碍物过多时，移动机器人无法越过较大的斥力势场进而到达不了目标点。

1.2 改进的人工势场法

本文的机器人是一款智能小车，采用八方位遍历每个路径点最小势能的方法改进，即：从智能小车当前位姿出发，计算出正前方、东北方，西北方，正左方、正右方、东南方、西南方、正后方分别移动一个步长时各点的势能，并选择其中势能最小点作为下一步位姿。

针对几个障碍物零散排布在小车与目标点之间导致出现局部势能极小值点，从而使小车的行驶路径在两点之间反复振荡的情况，引入模拟退火算法[7]，使其跳出振荡点，从而脱离局部势能极小值点[8]；针对目标点周围障碍物过多，导致目标点不可达的问题，提出了一种基于碰撞预测及有效障碍物的算法来解决目标点不可达的问题。

1.2.1 模拟退火算法解决局部势能极小点

（1）算法流程

步骤1：记录智能小车每一步的位姿，并判断出下一步的位姿是否与上一步位姿为同一位置，若是，则转入步骤2；若否，则转入步骤3。

步骤2：启用模拟退火算法，该算法分为3 步。第1 步，若当前位姿的下一位姿与上一位姿处于同一位置，将当前所处位姿纪录为point，在point 附近选择随机点x（x 为以point 为圆心，1 个步长为半径的圆上的点）作为初始点，并计算该点势能xout；再在x 附近选择随机点y（y 是以x 为圆心,1个步长为半径的圆上的点），若y 移动到point 上则令其势能yout为无穷大；否则进行第2 步。第2步，计算出小车当前的势能yout，并将其与上一步的位姿比较。计算两者势能之差Δ=xout-yout。若Δ>0，令x=y，f（x）=f（y）。若Δ<0,则执行第3步。第3 步，理论概率为

当P>rand（0，1）时，令xout=yout，x=y，执行步骤3；否则，删除该随机点，重新执行步骤1。

步骤3：判断智能小车是否已经摆脱震荡点，即当前位姿的下一位置与上一位置处于不同位姿，否则，返回步骤1。

（2）仿真实验分析

为了验证文中所提出的模拟退火算法的有效性，利用MATLAB 工具分别对传统的人工势场法与改进的人工势场法进行仿真分析。

仿真参数设置为：引力势场增益系数katt=40；斥力势场增益系数krep=100；计算步长l=0.1；循环次数为200 次，障碍物的影响距离为2 m，小车的起始位姿为（0，0），目标点的位置为（6，8）；传统人工势场法的仿真图片如图3 所示。

图3 传统人工势场法小车路径Fig.3 Vehicle path of traditional artificial potential field method

由图3 可见，传统的人工势场法中当智能小车与目标点之间存在零散障碍物时，可能会出现局部势场极小值点而产生振荡的情况，导致小车无法逃脱该点，不能到达目标点的问题。

改进之后的人工势场法中仿真参数设置：退火算法中控制参数初值T0=20，衰减因子∂=0.99，步长为0.1，迭代次数为1 000 次。其余参数与传统人工势场法参数相同，改进后的仿真图片如图4 所示。

图4 退火算法小车路径Fig.4 Vehicle path with annealing algorithm

从图4 可以看出，加入模拟退火算法的人工势场法克服了局部势能极小值点的问题，成功规避了障碍物到达目标点。

1.2.2 碰撞预测算法判断障碍物失效解决目标点不可达问题

（1）行驶路径上障碍物过多

当智能小车与目标点之间存在密集的U 型或L型障碍物时，小车无法越过高斥力势能场进而到达目标点。此时这些障碍物会形成一个局部势能极小区域[9]而非局部势能极小值点，导致退火算法失去效果，如图5 所示。

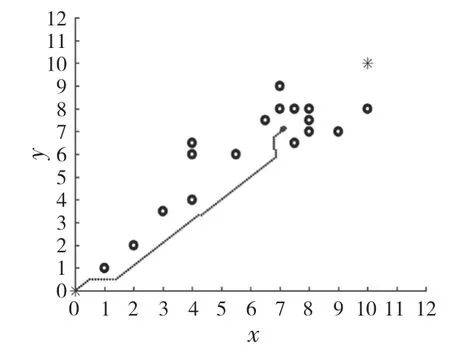
图5 加入退火算法的人工势场法Fig.5 Artificial potential field method with annealing algorithm

解决方法：实际工况下，陷入单个局部势能极小值点的情况较少，所以退火算法的作用次数一般较少，当退火算法使用次数>3 时，可能就陷入了局部势能最小区域，即障碍物密集区域，把退火算法使用次数counter=3 时作为一个临界点，设置一个计数器counter，令其初始值为0，每使用一次退火算法其值加1，当退火算法的使用次数>3 时，便执行碰撞预测算法[10]。

碰撞预测算法：设置一个预测距离[11]。当多个障碍物与小车距离小于该预测距离时，令小车以当前位置为圆心，选择一个半径和偏转角度，设置一个虚拟目标点逃脱该陷阱障碍物。算法流程：

第1 步：起点处或到达虚拟目标点后counter置为0，使用一次退火算法则counter+1，counter>3时执行第2 步，否则，执行第5 步。

第2 步：设置一个安全预测距离sfrep。计算各障碍物距小车的距离，并记录距离小于预测距离的障碍物，本文中将该类障碍物称为“陷阱障碍物”，由于最少4 个障碍物便可形成一个L 型障碍物，所以当陷阱障碍物个数≥4 时，执行第3 步。否则，执行第5 步。

第3 步：在陷阱障碍物中，以智能小车当前位置为圆心，小车到距离最远的陷阱障碍物的距离为半径，找到小车最右侧的陷阱障碍物，并以此障碍物为基准再向右偏转9°,设置虚拟目标点，若该虚拟目标点与障碍物重合，则再偏转3°设置障碍物，以此类推。

第4 步：智能小车向虚拟目标点移动。

第5 步：遍历8 个方向寻找势能最低点，作为下一位姿。执行第1 步。

仿真实验分析：为了验证本文提出的碰撞预测算法的可实施性，利用MATLAB 工具在U 型障碍物下分别对加入退火算法的人工势场法以及在此基础上再加入碰撞预测算法的人工势场法进行比较。

加入退火算法改进方法的仿真参数设置：引力势场增益系数katt=40；斥力势场增益系数krep=100；计算步长l=0.1；循环次数为200 次，障碍物的影响距离为2 m，小车的起始位置为（0，0），目标点的位置为（10，10）；退火算法中控制参数初值T0=20；衰减因子∂=0.99，步长为0.1，迭代次数为1 000 次。在U 型障碍物下，只加入退火算法的人工势场法的仿真结果如图5 所示。

在退火算法的基础上再加入碰撞预测算法的人工势场法的仿真参数为：安全预测距离为sfrep=1.5，陷阱障碍物最大个数danobs=4，其余参数配置跟加入退火算法的人工势场法一致，仿真结果如图6 所示。可见，加入退火算法的人工势场法在小车到达目标点之前有较多障碍物时，小车会绕一定区域振荡，即退火算法只能够应对局部势能最小值点问题，难以解决局部势能最小区域问题；加入碰撞预测算法后智能小车则创建了一个虚拟目标点，即图6 中三角区域，有效规避了U 型障碍物，具有较好的可实施性。

图6 在退火算法基础上加入碰撞预测算法的人工势场法Fig.6 Artificial potential field method with collision prediction algorithm added to annealing algorithm

（2）目标点周围障碍物过多

当障碍物不在小车到达目标点的路径上，而在目标点周围时，此时当小车接近目标点时会有较大的斥力势场，进而导致目标点不可达。

解决方法：计算小车当前位置与目标点间的距离dit 以及与障碍物间的距离dio，当dio>dit 时，则判断该障碍物失效，令其对小车产生的势能为0。

进行仿真以验证其有效性。传统仿真结果如图7 所示，加入失效障碍物后的仿真结果如图8 所示。图7、图8 起点为（1，1），目标点为（4.5，4.5）。结果表明，该方法有效解决了障碍物在目标点周围所形成势场过大导致目标点不可达的问题。

图7 传统的人工势场法目标点周围存在障碍物情况Fig.7 Obstacles existing around target point of traditional artificial potential field method

图8 加入失效障碍物后的人工势场法Fig.8 Artificial potential field method with failed obstacles

综合以上2 种方法，有效解决了人工势场法中因目标点周围障碍物以及路径上陷阱障碍物过多而导致的目标点不可达问题。

2 智能小车多目标点路径规划

2.1 智能小车移动模型的建立

实际工作中的移动机器人，例如物流机器人[12]往往途经多个需要停留作业的目标点，而不是单一目标点，因此本文根据上述改进的人工势场法提出一种多目标点的路径规划方法。

在智能小车的移动过程中，设定一个初始点以及多个目标点，以目标点横坐标为依据，每次从小到大选择一个有效目标点，且每次设置一个目标点后，其余目标点对小车所形成的引力势能都为0。当一个目标点到达后，此目标点作为下一目标点的起始点，以每次的起始点为圆心，以起始点到目标点的距离为半径绘制一个圆形区域，在区域内的障碍物则被认定为本次移动过程中的有效障碍物，如图9 所示，以此来简化移动过程中对障碍物的计算，同时还可以减少目标点周围的障碍物个数，消除部分造成目标点不可达的因素。

图9 智能小车移动模型Fig.9 Smart car moving model

图9 中，以从左往右第1 个三角形为起始点，其余2 个为目标点，小圆形则为障碍物。3 个圆弧形所包围的范围分别代表3 次移动过程中有效障碍物的范围。从图9 可以看出：从起点到第1 个目标点的过程中，该方法减少了移动过程中对小车不起作用的障碍物的计算；从第1 个目标点到第2 个目标点的过程中，该方法排除了目标点周围部分障碍物的影响，将改进的人工势场法运用到该模型上进行多目标点路径规划。规划策略流程如图10 所示。

图10 路径规划流程图Fig.10 Path planning flowchart

2.2 改进方法在小车移动模型上的仿真

为了验证改进的人工势场法在所建立的智能小车移动模型上是否适用，对其进行仿真分析，仿真参数设置为：引力势场增益系数katt=40；斥力势场增益系数krep=100；计算步长l=0.1；循环次数为200 次，障碍物的影响距离为2 m，小车的起始位姿为（0，0），目标点的位置分别为（3，5），（6，8），（7，7），（10，10）；退火算法中控制参数初值T0=20，衰减因子∂=0.99，步长为0.1，迭代次数为1 000 次。安全预测距离sfrep=1.5，陷阱障碍物最大个数danobs=4。在此基础上进一步完善障碍物失效条件，即dio>dit 时，障碍物对小车所产生的人工势能为0。仿真结果如图11 所示。

图11 基于改进人工势场法的多目标点路径规划Fig.11 Multi-objective point path planning based on improved artificial potential field method

仿真结果表明，在智能小车多目标点移动模型上，改进的人工势场法可以有效到达各目标点,在由坐标点（7，7）到（10，10）的过程中，通过产生虚拟目标点有效地逃出陷阱障碍物所组成的U形区；由坐标点（6，8）到（7，7）的过程成功越过了中间的障碍物；顺利地克服了目标点不可达的问题，且全程没有出现因局部势能极小值点而导致小车在两点间反复振荡的现象，说明该算法在多目标点模型上具有良好的适用性。

3 结论

传统的人工势场法存在局部势能极小值问题和目标点不可达问题，本文通过对传统的人工势场法进行改进解决了以下问题：

（1）引入了模拟退火算法（控制参数初值T0=20，衰减因子∂设置为0.99）解决了局部势能极小值问题；（2）引入碰撞预测算法（安全预测距离sfrep=1.5，陷阱障碍物最大个数danobs=4）解决了行驶路径上障碍物过多目标点不可达问题；（3）比较小车与障碍物的距离与小车与目标点间的距离，进一步完善了障碍物失效的条件，解决了目标点周围因障碍物过多不可达的问题。

将改进后的人工势场法引入到所建立的智能小车多目标点移动模型上，最后得到了理想的仿真结果。