基于数据驱动模型的季节性河流洪水预警研究

冯公伟 ，蒋东进

（1.昌吉水文勘测局，新疆 昌吉 831100；2.水利部南京水利水文自动化研究所，江苏 南京 210012）

0 引言

随着全世界范围内各种洪水灾害的愈加频繁与严重，各种洪水预警方法研究也在不断推进[1-2]。对洪水灾害进行及时有效的预警，提高全社会的抗洪水平，保证周边居住地区的防洪安全是建立河流洪水预警系统的主要目的。传统的河流洪水预警方法（以下简称传统预警方法）通常根据气象参数、气象报告、洪水特性、水文条件及河流径流量等实现预警，被广泛应用于水文预报业务中[3]。传统预警方法一般利用集中式[4]和分布式的水文预测模型[5]，通过对降雨量、河道汇流、下垫面渗透率的预测计算，模拟得到河流的渗流情况，进而推断出洪水出现时机及持续时间，实现季节性河流洪水预警。传统预警方法比较依赖水文站点的历史水文数据资料，虽然在一定程度上可以对洪水进行预警，但由于各地区水文条件的不同，降雨量和地表径流量通常具有多变性，难以精准预测和把握变化趋势，因此传统预警方法预测出的水位变幅值与实际值存在一定的差距[6]，导致预警精度下降。且传统预警方法需要利用大量的历史水文洪水数据进行统计分析，计算过程中涉及的参数较多，导致计算量较大，计算速度和模拟精度通常不高，计算过程中还容易受到不确定可变因素的影响，无法对季节性河流的洪水情况进行精准预测和预警，预估洪水等级时容易出错，进而影响防洪决策。

数据驱动模型通过建立非线性映射函数，可对洪水等级进行精准预估，提高预警准确率。因此为保证预警精度，将数据驱动模型应用于实际的季节性河流洪水预警方法设计中，提出一种基于数据驱动模型的季节性河流洪水预警方法（以下简称本研究预警方法），为流域预报等工作提供参考[7]。

1 本研究预警方法分析

1.1 河床汇流率计算

河床汇流指季节性河流在河床内部的集中过程[8]。河床汇流率是单位时间内通过河道某一截面的水量，受到降雨量、地貌、植被覆盖、土壤类型等因素的影响。在水文学中，河床汇流率是评估水资源利用、洪水预测和水文模型建立的重要指标之一。计算汇流率，可以掌握季节性河流的地表与地下径流情况，为洪水预警提供数据基础。利用径流曲线法（SCS 法）可计算洪水过程中的地表径流，其中降雨历时tp与洪水洪峰延时td之间的关系表达式如下：

一般情况下，汇水区在固定面积内因降水产生的地表径流的洪峰流量与延时之间的关系表达式为

式中：A为单位流域汇水面积；Qm为标准情况下的洪峰流量值；Cp为洪峰系数，一般取 0.85；ΔQ为始末出流量之间的差值；Am为河流的横截面面积。

根据 SCS 法，可以求出河流洪峰峰值与峰值时间之间的关系，具体关系表达式为

式中：V为河道容积；tz为峰值时间。tz可用固定面积内的降水历时与洪水的洪峰延时表示，具体表达式为

则河床汇流率Rp计算公式如下：

式中：i表示降雨时段。i=1 表示降雨时段第一时间点。

根据式（1）～（5）可求得季节性河流的河床汇流率，将该汇流率作为辅助函数，即可构建神经网络水文模型[9]。

1.2 预警模型构建

本研究以数据驱动模型为基础进行季节性河流洪水预警，数据驱动模型具体工作原理图如图1 所示。

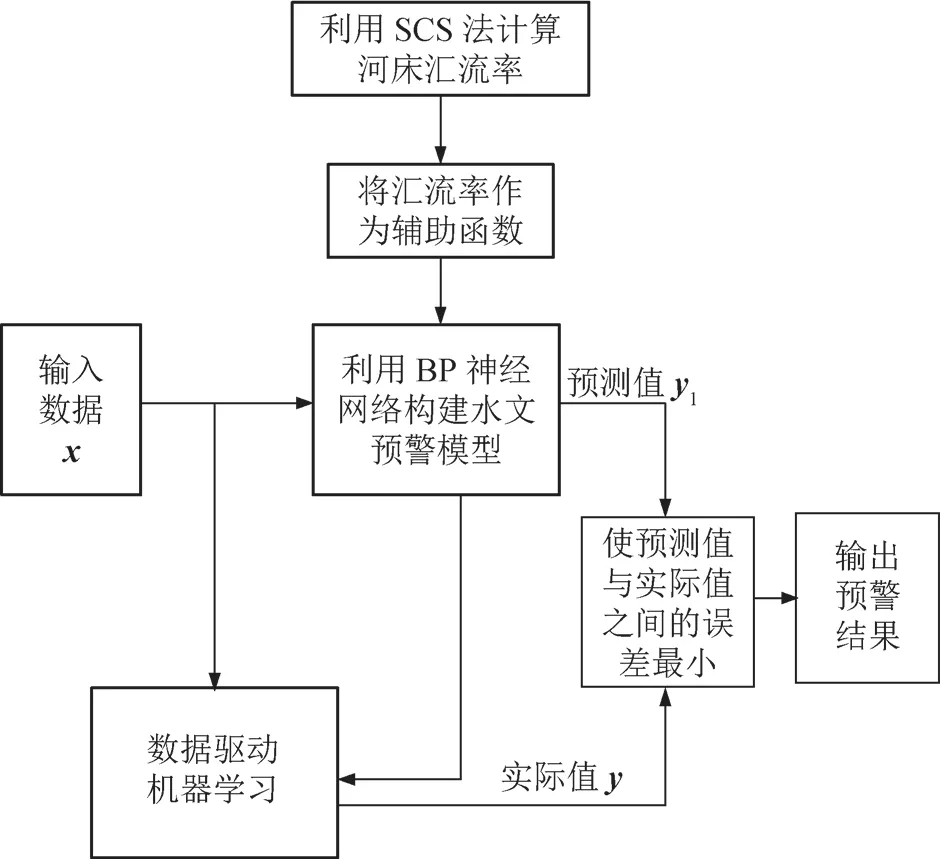
图1 数据驱动模型工作原理图

通过图1 工作原理可知，数据驱动模型通过数据驱动构建对应的模型，并通过机器学习不断减少实际值与预测值之间的误差，因此对于解决季节性河流洪水预测类的问题具有较大优势。BP 神经网络模型作为数据驱动模型中的一种，可广泛应用于洪水预警中。在利用数据驱动模型对季节性河流洪水进行预测之后，可利用 BP 神经网络构建水文预警模型[10]。

假设季节性河流洪水的时间序列输入向量为x，且满足x∈Rd（Rd表示河床汇流率d个参数集合），则 BP 神经网络输出层可用高斯函数激活，将河床汇流率作为辅助函数，具体公式如下：

式中：Ri（x）为神经元数量为i时的输出值；ci为高斯函数的稳定系数；a为激活次数。

对 BP 神经网络输出层进行加权求和，具体公式如下：

式中：h为隐藏节点的实际个数；wij为从隐藏层到输入层的参数权重；yj为输入节点个数为j时的输入值；q为隐藏节点的初始个数。

采用希尔特函数缩小误差，具体公式如下：

式中：σ为权重向量的方差；ymin为加权求和误差的最小值；E（yj）表示相对误差函数。

构建极限向量误差模型输出量oj，具体公式如下：

式中：j的取值范围为[1，m]，下标j和yj的下标j的取值范围一致；g（x）为激活函数；bi为神经元个数为i时的偏差值。

将偏差值作为目标函数，即可构建神经网络水文预警模型，具体公式如下：

式中：Q为洪水流量；Pr为季节性河流流域内的降雨量；Δtc代表不同时间段之间的间隔；x与y的取值范围为x∈[1，0]，y∈[1，0]；Ff为非线性激活映射函数。

根据式（6）～（10）可构建基于数据驱动的水文预警模型，对模型进行求解，计算季节性河流的预警值。为便于直观展示预警结果，需要设定洪水预警规则[11]。采用传统的洪水预警信号规则进行规划，用蓝、黄、红表示严重程度不同的洪水预警等级，其中：蓝色代表洪水等级最低，危害最小；红色代表洪水等级最高，危害程度最严重；黄色代表中度洪水等级。

将 3 种预警信号参数分别设置为[-3，-3，0]，[-1，0，1]，[0，3，3]，其中 0，1，3 分别表示利用构建的基于数据驱动的水文预警模型得到的预警值，预警值越高，预警等级越高。具体预警隶属效果图如图2 所示。

分析图2 可知，通过确定不同预警信号的隶属度，可得到相关的预警值，并及时输出预警结果，以保证季节性河流洪水预警的效率。至此，完成基于数据驱动模型的季节性河流洪水预警方法设计。

2 试验验证

为更好地说明本研究预警方法的实际应用效果，进行试验测试，对实际预警效果进行分析。

2.1 试验环境描述

本次试验以某市主干道河流右岸的一条支流为试验对象。该支流流向为东北到西南，发源于临市海拔 840 m 的高山，整条河流长度为 56 km，流域面积在 500 km2以上，沿岸有6条支流汇入。上游河谷较为狭窄，下游河谷较为宽阔，下游河口的深度为1.2 m，宽度为 18 m，自然落差为 800 m，属于大中型河流。同时受该市地理位置的影响，河流属于温带季风性气候，夏季温和多雨，冬季干燥少雨，河流流量呈季节性波动，流量特征符合季节性河流的特点，一般在汛期会出现洪峰，延迟时间一般在 25～45 min 内。每年的平均降雨量为 528.5 mm，汛期时的降雨量占全年降雨量的 65% 以上，属于典型的雨洪径流。

本次试验选取传统预警方法为对比对象。为提高试验结果的可靠性，选取该河流近 5 a 的水文数据，共 15 次双峰型洪水数据作为历史数据，统计每年降雨的开始及停止时间，记录水位的起涨时间、洪峰延时、平均降雨量、水位涨幅大小、洪峰持续时间及地表径流等水文数据，为 2 种洪水预警方法提供数据支持。通过对子流域水文参数的模拟设定对洪水进行预警，具体模拟参数如表1 所示。

表1 研究子流域水文参数

通过预测水位变幅，比较预测值与实际测量值之间的拟合程度，拟合效果越好代表预警方法的精度越高，季节性河流洪水预警效果越好。

2.2 试验结果

利用2种预警方法对表1中8个子流域进行季节性河流洪水预测，检验不同预警方法的预测值与实际测量值的拟合程度，试验结果如图3所示。

图3 预测值与实际测量值的拟合情况

根据实验结果可知，针对涨幅程度不同的洪水，不同预警方法预测出的水位变幅值与实际测量值的误差也有所不同。传统预警方法预测出的水位变幅值与实际测量值之间的平均误差一般为 23 mm，并且因洪水强度的不同存在较大差异。在对强度较大的洪水进行预警时，预测出的水位变幅值与实际测量值之间的差值也会上升，说明传统预警方法会受到实际洪水情况与水文条件变化的影响而产生不同程度的偏差，无法对季节性河流洪水进行精准预警。本研究预警方法预测出的水位变幅值与实际测量值的拟合效果明显优于传统预警方法，实际测量值与预测值之间的误差较小，保持在 100 mm 以内，并且本研究提出的季节性河流洪水预警方法不受洪水强度的影响，预警误差值不会随着洪水强度的增大而出现更大的偏差，说明本研究预警方法的稳定性较高，在预警精度上要优于传统预警方法。这是由于本研究预警方法与数据驱动模型进行了有效结合，通过数据驱动水文预警模型，提高了预测精度，因此可以保证对季节性河流洪水进行精准预警，可应用于实际的水文预报业务中，为洪水预警研究提供积极的帮助。

3 结语

本研究提出的季节性河流洪水预警方法与数据驱动模型理论进行了有效结合，选取数据驱动模型进行河流洪水预测，结合预测结果与 BP 神经网络构建数据驱动水文预警模型。试验结果表明，本研究预警方法预测的水位变幅值与实际测量值的拟合效果明显优于传统预警方法，实际测量值与预测值之间的误差较小，实际应用效果较好。本研究预警方法有利于对各种水文灾害进行实时监测，掌握河流的水文情况，提高对气象灾害的预测和防范水平，减少因气象灾害造成的经济损失。对研究同等类型的山洪、滑坡等气象灾害的预警和防范具有积极的借鉴意义，可为洪水风险评估提供技术上的帮助，对我国防震减灾工作的建设具有积极的推进作用。