考虑接触问题的多边形有限元重力坝抗震断裂研究

徐强 董金凯 陈健云 李静

摘要：

抗震断裂问题是混凝土重力坝的重要研究内容，数值模拟则是针对此类问题的主要研究方法，现有断裂算法存在计算效率较低，大多未考虑接触等问题。为此，构造了高效的平均值坐标插值多边形单元和接触薄层单元，并将二者耦合后用于结构裂缝扩展的数值模拟。该方法将具有奇异特性以及复杂几何区域网格自适应性强的多边形有限元方法与平均值坐标插值方法、局部多边形网格策略结合起来模拟裂缝扩展；通过等参子三角形方法进行数值积分，求解刚度矩阵；基于最大周向应力准则，采用混合断裂强度因子作为起裂判据；针对裂缝面间的接触问题，引入张剪状态下的黏聚力模型以及压剪状态下的光滑接触模型。基于上述方法，通过Matlab编程的方式开发出一套能模拟裂缝扩展的程序，并通过对含边裂缝的PMMA板试验和含预设裂缝的四点剪切梁试验的模拟，验证了程序的准确性与有效性。最后，以含有预设裂缝的柯伊纳混凝土重力坝为例，对其在是否考虑接触问题下裂纹扩展的情况进行了对比分析，结果表明该程序模拟裂缝真实准确，具有计算速度快、结果文件小等独特优势。

关 键 词：

混凝土重力坝； 平均值坐标插值多边形有限元； 裂缝扩展； 接触算法

中图法分类号： TV642.3；TV313

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2023.08.030

0 引 言

中国水能资源十分丰富，位居世界首位。水电具有循环再生、长期成本低、综合效益大等优点。重力坝是中国高坝建设的主要坝型，其多位于西南、西北等强震频发的地区，而地震则是造成其损伤断裂破坏的主要潜在危险。从大坝的断裂过程来看，结构损伤裂缝往往从坝体表面开始，在施工阶段已经形成。在地震作用下，表面裂缝很有可能继续发展，深入坝体。因此，大坝安全评价的首要问题是确定已有裂缝是否会扩展，预测在各种可能条件下的扩展路径以及危险程度，以便在它们进一步扩展前采取控制措施［1］。

由于重力坝具有体积大、受力情况复杂等特点，现阶段主要利用数值模拟的方法对其进行研究。近年来，很多学者针对混凝土重力坝断裂问题进行了多方面研究［2-4］。王超等［5］和Siva等［6］探讨了在地震作用下初始裂缝的位置以及深度对坝体的影响。在对结构进行损伤断裂数值模拟时，有限元方法作为一种重要手段，已经广泛应用于工程领域和学术研究中。二维有限元方法中使用的基本单元形状为三角形和四边形。三角形单元为常应变单元，而四边形单元对复杂几何区域离散比较困难，使得传统有限元对于一些特定的问题求解有明显的缺陷。将多边形单元用于有限元分析中能克服传统有限元的某些缺陷。Wachspress［7］首次在凸多边形单元上构造了有理多项式插值函数，用于在有限元分析中计算多边形单元的形函数；Floater［8］基于多边形单元的重心坐标提出平均值坐标法，适用于计算任意凸多边形和凹多边形的插值函数；Sukumar［9］基于最大熵方法推导了任意多边形单元更为一般的插值函数；多边形有限元各向异性的特点使它在解决裂缝扩展［10］、断裂［11］等方面更加方便有效。Tabarraei和Sukumar［12］将自然邻点形函数应用于扩展有限元（X-FEM）中以模拟裂缝的扩展；Manzini等［13］研究了各种凸多边形有限元以及凹多边形有限元的性能，使其能用于裂尖以及裂缝的扩展的模拟；Natarajan等［14］、Mousavi等［15］、Talischi和Paulino［16］对凸多边形有限元以及凹多边形有限元数值积分规则进行了许多研究，使之可以用于模拟裂缝两侧的单元积分；Ooi等［17-18］提出用基于多边形单元的比例边界有限元法模拟结构裂缝扩展；Spring［19］和Leon［20］等人将多边形有限元方法用于黏弹性动态断裂问题中。施明光等［21］采用多边形比例边界有限元，结合基于拓扑的局部网格重剖分方法，首次模拟了复合材料裂缝扩展。在裂缝扩展过程中，由于受力状态不同，如果不考虑裂缝面上的接触条件，则不能反映裂缝的真实开裂状态以及导致有限元分析时网格相互嵌入的问题。针对张剪状态，Fang等［22］和伍江飞［23］对黏聚裂缝模型进行了研究，并应用于混凝土断裂的模拟。针对压剪状态，薛冰寒等［24］提出了求解弹性摩擦接触问题的IGA-B可微方程组；Zhou等［25］和喻葭临等［26］基于扩展有限元方法，构造了与之相适应的接触算法；章鹏等［27］基于比例边界有限元，提出了一种在裂尖单元的裂缝面上采用边对边约束方法处理接触问题的方法。

由于常规单元在裂缝尖端不能反映裂尖的奇异性，而基于平均值坐标插值的多边形有限元具有1/4点的奇异性，同时平均值坐标插值的多边形有限元具有突出的几何拓扑性能，能更为准确地描述裂缝扩展路径。因而，平均值坐标插值多边形有限元常被用于模拟裂尖扩展。但是现阶段平均值坐标插值多边形有限元模拟裂尖仍存在以下问题：平均值坐标插值多边形函数复杂，应变矩阵计算复杂度高，刚度矩阵合成效率低；平均值坐标插值多边形单元，在模拟裂缝扩展时，大多没有考虑裂缝闭合的接触问题；裂缝扩展重剖分算法一般都比较复杂，计算效率较低。基于以上问题，本文采用等参元方法解决刚度矩阵合成效率低的问题；开发接触薄层单元并耦合平均值坐标插值多边形单元解决裂缝闭合的接触问题；使用一次裂缝跨越一个单元解决重剖分的几何复杂度的问题；最后通过Matlab编程实现了上述算法过程。

1 平均值坐标插值多边形有限元模型

1.1 多边形单元插值形函数的一般性质

4 数值算例验证

为验证上述裂缝扩展程序的合理性，本文选用文献［33］中所述的数值模拟中的两个算例进行对比分析，论证程序的正确性。

第一个算例为PMMA边缘裂缝板试验，其几何尺寸、边界条件、荷载条件如图7所示。材料弹性模量为3.86 GPa，泊松比为0.31，厚度为1 m，断裂韧度为1 MPa·m1/2。尺寸a=4 mm，c=5 mm，w=30 mm，h=45 mm。分别改变裂缝位置d=6，10 mm和14 mm，研究裂缝位置对裂缝路径的影响。假定为平面应变条件。本文所述程序模拟裂缝结果与文獻［33］模拟裂缝结果对比情况如图8所示。

第二個算例为含预制裂缝的四点剪切梁试验，该试验已成为验证混合型裂缝扩展模型的基准。材料弹性模量为24.8 GPa，泊松比为0.18，厚度为0.152 m，断裂韧度为1.65 MPa·m1/2。假定为平面应力状态。具体尺寸、荷载条件等情况如图9所示。应用本程序计算的裂缝路径及扩展情况与文献［33］所述情况对比如图10所示。

经过两个算例的对比分析可见，两个算例的裂缝路径以及开裂情况均与本文所用程序计算结果相吻合。因此，论证了该断裂程序搜索断裂路径的正确性与合理性。

5 重力坝裂缝扩展模拟

印度的柯伊纳混凝土重力坝是坝体在地震作用下遭受到破坏的典型实例之一，可在一定程度上反映坝体的裂缝扩展情况。国内外很多学者对柯伊纳混凝土重力坝在地震作用下的动力响应进行了深入研究。因此，本文选用该混凝土重力坝，利用本文方法编制的程序，对其进行裂缝扩展模拟的研究。

柯伊纳混凝土重力坝，坝高103 m，坝顶宽14.8 m，坝底宽70 m，坝高66.5 m处下游坝面出现折坡。为使计算结果具有较高的精度，采用在坝基与坝体边缘处加密的有限元模型，如图11所示。断裂分析过程需要设置初始裂缝，所以断裂过程就是裂缝扩展过程，初始裂缝设置在下游折坡处下，裂缝长度0.5 m。坝体混凝土材料的弹性模量为20 GPa，泊松比为0.167，密度为2 400 kg/m3，抗拉强度为2 MPa，断裂能为200 N/m，混凝土断裂韧度取为2.747 MPa·m1/2。

外荷载主要考虑重力、静水压力（静水压力水位为91.75 m），以及地震作用。地震采用柯伊纳地震实测波，考虑峰值加速度约为0.5g的水平方向地震动与峰值加速度约为0.3g的垂直方向地震动同时作用（见图12）。

5.1 基本步骤

基于平均值插值多边形有限元方法，考虑裂缝面接触问题，给出了工程实例在实测地震动作用下裂缝扩展模拟的情况，程序具体实施过程如下：

（1） 首先利用ANSYS建立坝体有限元模型，施加荷载，约束节点。求解后，读出单元属性信息，并导入Matlab中，通过Matlab编程对节点施加静力和动力荷载。

（2） 根据输入实测地震动进行时程计算，计算得到初始裂缝扩展角，转入动力裂缝求解程序，对裂缝单元重剖分，剖分为一个五边形单元、一个三边形单元加一个五边形单元，或者剖分为一个五边形单元与两个四边形单元。

（3） 动力裂缝求解过程中，考虑裂缝面间的接触问题，因此，利用接触算法求解附加刚度矩阵，与整体刚度矩阵叠加后进行迭代，计算真实开度。此算法既考虑了张开时的黏聚力影响，又防止出现闭合时单元相互嵌入的问题。

（4） 通过时程计算，利用动力裂缝求解程序，判断裂缝扩展方向，确定裂缝扩展路径，完成对裂缝扩展情况的模拟。

5.2 裂缝扩展模拟情况分析

由于开裂，将裂缝附近单元重新剖分为独立单元，在地震加载过程中，单元会存在相互嵌入的问题。因此本文采用前述接触算法应用于柯伊纳混凝土重力坝裂缝扩展模拟分析，成功解决了模拟过程中相互嵌入的问题（见图13）。

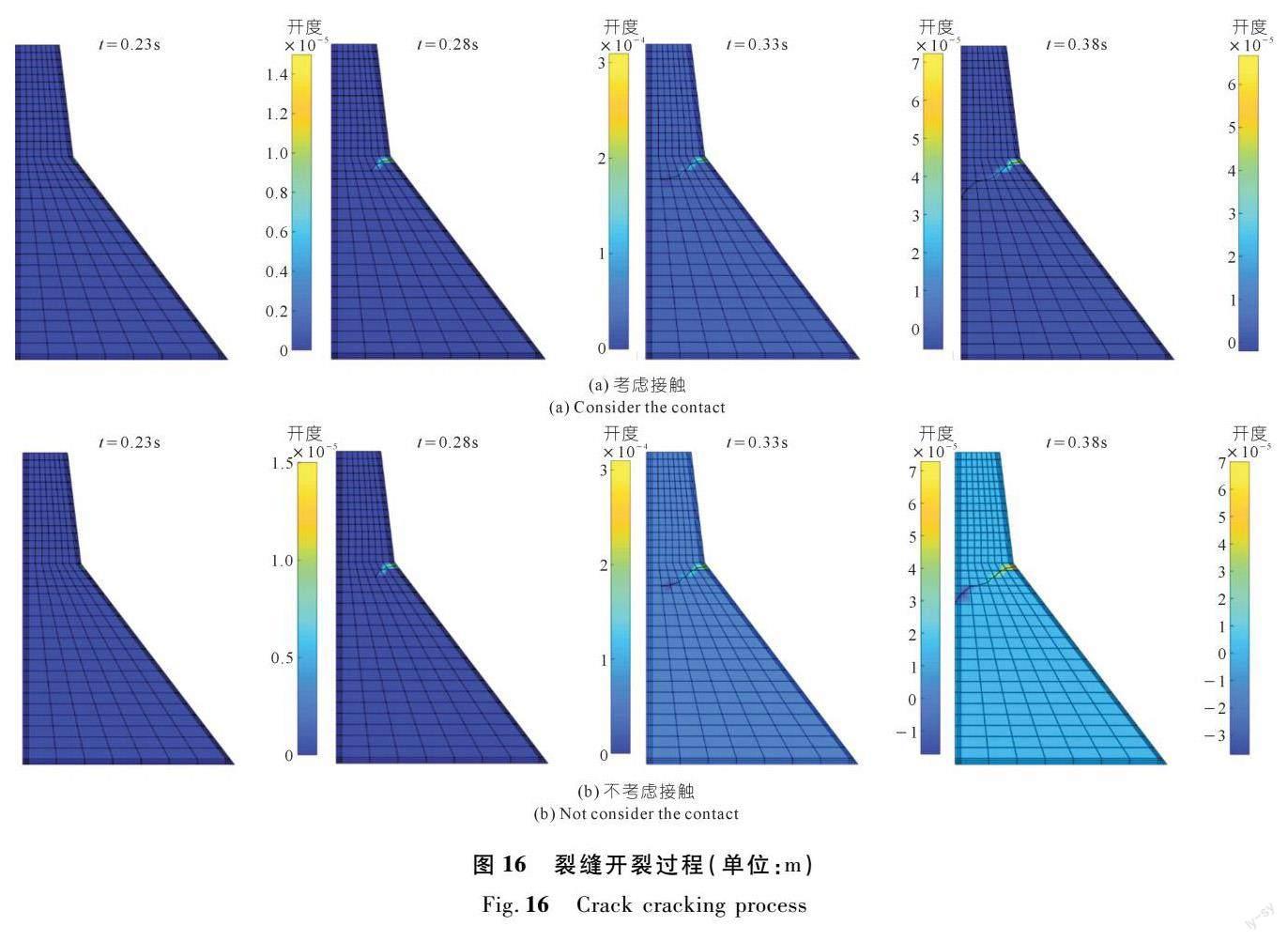
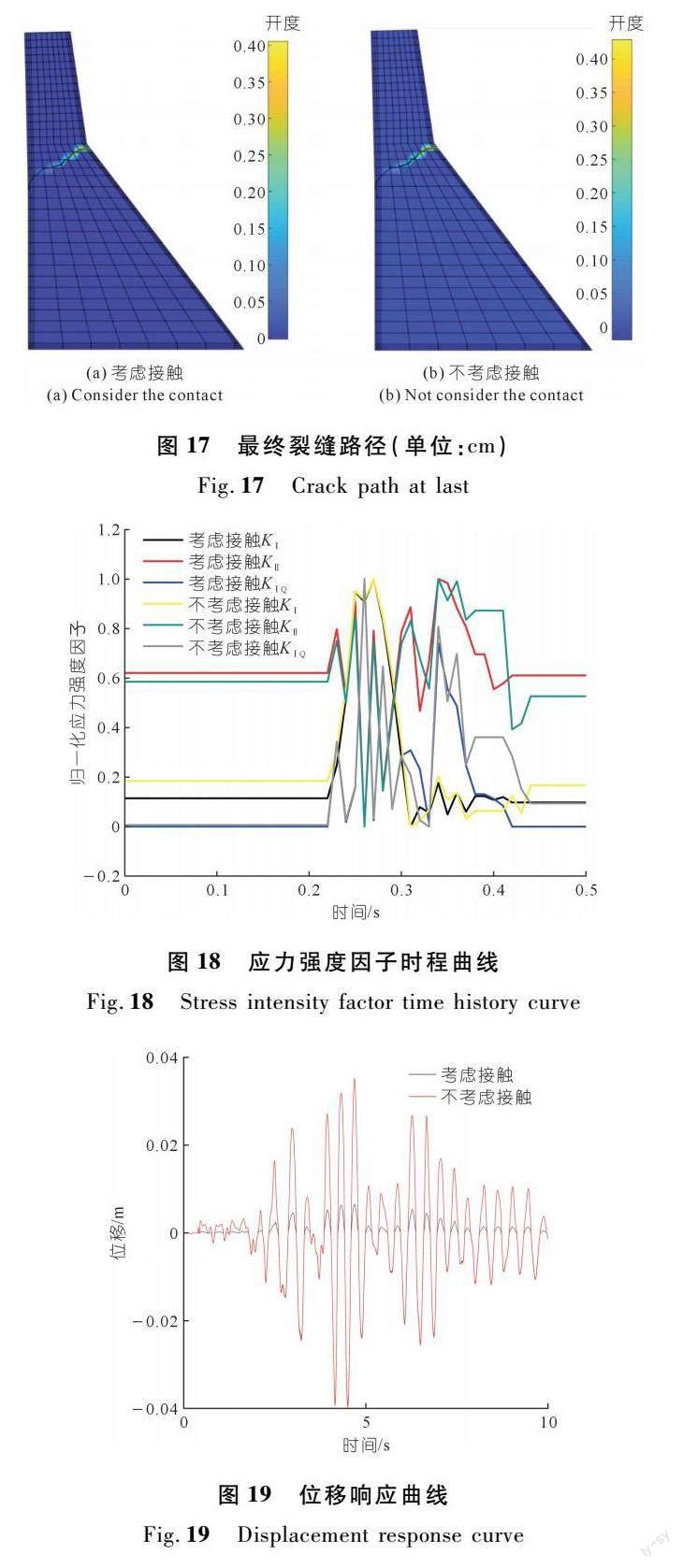
对是否考虑接触问题的裂缝扩展情况进行模拟分析，开裂过程取初始裂缝处为开度时程监测点，如图14所示，其缝面张开闭合时程曲线如图15所示。具体开裂过程如图16所示，最终裂缝路径如图17所示。可以看出，本文提出的接触算法，消除了地震过程中缝面的负开度，既解决了缝面间的嵌入问题，同时又提高了裂缝扩展模拟的准确性。

通过对应力强度因子时程曲线（见图18）进行分析，可以发现，裂缝均于0.22 s时开裂，裂缝扩展速度很快，均在0.5 s内开裂完成。开裂过程为Ⅰ型和Ⅱ型耦合作用。考虑接触情况下，开裂速度略快，等效应力强度因子峰值出现略晚且小于不考虑接触情况。

由于竖直方向位移响应非常微小，故仅对水平方向位移响应进行分析，如图19所示。可以发现，考虑接触的情况下，大大减小了x轴正向位移，也反映出接触算法的作用。

6 结 语

本文基于多边形有限元理论，考虑裂缝接触面模型，利用Matlab开发了裂缝扩展模拟的程序。并通过对PPMA边裂缝板试验以及含预设裂缝的四点剪切梁试验的裂缝扩展情况进行模拟，验证了该程序的正确性。随后，利用该程序对是否考虑接触问题情况下的柯伊纳混凝土重力坝裂缝扩展问题进行对比分析，研究考虑接触问题后如何解决单元相互嵌入的问题。

该程序采用平均值坐标插值多边形有限元在关心的复杂几何区域进行网格划分，具有网格自适应性强的优点；由于平均值坐标插值多边形有限元节点应力值为奇异解的特性，将其应用于坝体断裂分析具有较高的精度；采用等参元方法使平均值坐标插值多边形有限元的计算效率大幅提升；采用裂缝面不同状态下的接触算法，很好地模拟了接触界面上的粘结与分离，更真实地模拟了裂缝开裂情况。同时该程序还具有计算速度快、结果文件小、适用性强等优点。

参考文献：

［1］ 杜效鹄，段云岭，王光纶.重力坝断裂数值分析研究［J］.水利学报，2005（9）：1035-1042.

［2］ 卿龙邦，喻渴来，徐东强.基于扩展有限元法的混凝土重力坝宏细观断裂数值分析［J］.水力发电学报，2017，36（6）：94-102.

［3］ 暴艳利，钟红，林皋.基于多边形比例边界有限元的重力坝地震断裂模拟［J］.水电能源科学，2015，33（4）：72-75，42.

［4］ 钟红，牟昊，张文宣.基于有限断裂法和比例边界有限元法的裂纹扩展模拟［J］.计算力学学报，2017，34（2）：168-174.

［5］ 王超，张社荣，王高辉.初始裂缝对重力坝地震响应特性的影响［J］.天津大学学报（自然科学与工程技术版），2016，49（4）：392-399.

［6］ SIVA P，MAHESH M，RAJ K D，et al.Critical crack lengths of concrete gravity dam by using fracture mechanics［J］.Materials Today：Proceedings，2021，38（5）：3149-3159.

［7］ WACHSPRESS E L.A Rational finite element basis［J］.Journal of Lubrication Technology，1975，98（4）：635.

［8］ FLOATER M S.Mean value coordinates［J］.Computer Aided Geometric Design，2003，20（1）：19-27.

［9］ SUKUMAR N.Construction of polygonal interpolants：a maximum entropy approach［J］.International Journal for Numerical Methods in Engineering，2004，61（12）：2159-2181.

［10］ 張慧华，祝晶晶.复杂裂缝问题的多边形数值流形方法求解［J］.固体力学学报，2013，34（1）：38-46.

［11］ BISHOP J E.Simulating the pervasive fracture of materials and structures using randomly close packed Voronoi tessellations ［J］.Computational Mechanics，2009，44（4）：455-471.

［12］ SUKUMAR N，TABARRAEI A.Conforming polygonal finite elements［J］.International Journal for Numerical Methodsin Engineering，2004，61（12）：2045-2066.

［13］ GIANMARCO M，ALESSANDRO R，SUKUMAR N.New perspectives on polygonal and polyhedral finite element methods［J］.Mathematical Models and Methods in Applied Sciences，2014，24（8）：1665-1699.

［14］ NATARAJAN S，BORDAS S，MAHAPATRA D R.Numerical integration over arbitrary polygonal domains based on Schwarz-Christoffel conformal mapping［J］.International Journal for Numerical Methods in Engineering，2009，80（80）：103-134.

［15］ MOUSAVI S E，XIAO H，SUKUMAR N.Generalized Gaussian quadrature rules on arbitrary polygons［J］.International Journal for Numerical Methods in Engineering，2010，82（1）：99-113.

［16］ CAMERON T，GLAUCIO H P.Addressing integration error for polygonal finite elements through polynomial projections：A patch test connection［J］.Mathematical Models and Methods in Applied Sciences，2013，24（8）：1701-1727.

［17］ OOI E T，SONG C，TIN-LOI F，et al.Automatic modelling of cohesive crack propagation in concrete using polygon scaled boundary finite elements［J］.Engineering Fracture Mechanics，2012，93：13-33.

［18］ OOI E T，SONGC，TIN-LOI F，et al.Polygon scaled boundary finite elements for crack propagation modelling［J］.International Journal for Numerical Methods in Engineering，2012，91（3）：319-342.

［19］ SPRING D W，LEON S E，PAULINO G H.Unstructured polygonal meshes with adaptive refinement for the numerical simulation of dynamic cohesive fracture［J］.International Journal of Fracture，2014，189（1）：33-57.

［20］ LEON S E，SPRING D W，PAULINO G H.Reduction in mesh bias for dynamic fracture using adaptive splitting of polygonal finite elements［J］.International Journal for Numerical Methods in Engineering，2015，100（8）：555-576.

［21］ 施明光，徐艷杰，钟红，等.基于多边形比例边界有限元的复合材料裂缝扩展模拟［J］.工程力学，2014（7）：1-7.

［22］ FANG W H，WU J F，YU T T，et al.Simulation of cohesive crack growth by a variable-node XFEM［J］.Frontiers of Structural and Civil Engineering，2020，14（1）：215-228.

［23］ 伍江飞.基于黏聚裂缝模型的混凝土断裂过程扩展有限元法模拟［J］.水利水电技术，2019，50（4）：205-211.

［24］ 薛冰寒，林皋，胡志强等.求解摩擦接触问题的IGA-B可微方程组方法［J］.工程力学，2016，33（10）：35-43.

［25］ ZHOU X P，CHEN J W，BERTO F.XFEM based node scheme for the frictional contact crack problem［J］.Computers and Structures，2020，231：106221.

［26］ 喻葭临，于玉贞，张丙印，等.基于扩展有限元方法的界面接触算法［J］.工程力学，2011，28（4）：13-17.

［27］ 章鹏，杜成斌，江守燕.比例边界有限元法求解裂缝面接触问题［J］.力学学报，2017，49（6）：1335-1347.

［28］ 李术才，王兆清，李树忱.基于无理函数插值的多边形有限元方法［J］.山东大学学报（工学版），2008，38（2）：66-70.

［29］ HORMANN K.Barycentric coordinates for arbitrary polygons in the plane［R］.Clausthal-Zellerfeld：Institute of Computer Science，Clausthal University of Technology，2005.

［30］ KHOEI A R，YASBOLAGHI R，BIABANAKI S.A polygonal finite element method for modeling crack propagation with minimum remeshing［J］.International Journal of Fracture，2015，194（2）：123-148.

［31］ ERDOGA F，SIH G C.On the crack extension in plates under plane loading and transverse Shear［J］.Journal of Basic Engineering，1963，85：519-525.

［32］ 方修君，金峰，王进廷.用扩展有限元方法模拟混凝土的复合型开裂过程［J］.工程力学，2007（增1）：46-52.

［33］ YANG Z J.Fully automatic modelling of mixed-mode crack propagation using scaled boundary finite element method［J］.Engineering Fracture Mechanics，2006，73（12）：1711-1731.

（编辑：黄文晋）

Abstract：

Seismic fracture research is an important research content of concrete gravity dams.The numerical modeling is the main research method.Current fracture algorithms are inefficient and do not account the contact problems.In this paper，high efficiency polygonal finite element of mean value coordinate interpolation and contact thin layer element are constructed.The polygonal finite element method which is singularity and adapts well to complex geometries，is combined with the mean value coordinate interpolation method and the local polygonal mesh strategy to simulate the crack propagation.The stiffness matrix is solved by numerical integration using isoparametric sub-triangle method.Based on the maximum circumferential stress criterion，the hybrid fracture strength factor is employed as the crack initiation criteria.To address fracture surface contact，the cohesive force model in tension-shear and the smooth contact model in compression-shear are used.Based on the above methods，we use the Matlab to compile a program for simulating crack propagation.The program is validated by simulating PMMA plate tests with edge fractures and four-point shear beam tests with preset cracks.We present a comparative analysis of crack expansion with and without considering the contact problem for the Koyna concrete gravity dam in India，which has preset cracks.The conclusion is that the program has distinctive benefits such as realistic and accurate crack simulation，rapid calculating speed and small result files.

Key words：

concrete gravity dam；polygon finite element of mean value coordinate interpolation；crack propagation；contact algorithm