Cox 模型中几种变量选择方法对比研究

徐 习 赵鈺琳

（重庆工商大学数学与统计学院,重庆 400067）

Cox模型，也称为Cox比例风险回归模型，是一种用于分析生存数据的统计模型。它基于半参数模型，不需要对生存时间的概率分布做出假设，只需要假设风险函数的形式，从而可以对各种不同类型的生存数据进行建模和分析。在实际应用中，通常需要从大量的可能影响生存时间的变量中选择出对生存时间具有显著影响的变量，以便更准确地评估其对生存时间的影响。这就涉及Cox模型中的变量选择问题。对于变量选择，常常采用的方法是引入一些惩罚项来约束回归系数，从而达到减少变量数量、提高模型预测能力的目的。Cox模型中，常用的惩罚项有LASSO、Ridge、Elastic Net、SCAD等[1-3]。

变量选择在Cox模型的应用中具有重要意义，因为选取正确的变量可以更好地理解和预测生存时间，避免不必要的分析和浪费。然而，在实际应用中，由于变量间的相关性、数据质量等问题，变量选择也存在一些挑战。因此，选择适合的变量选择方法对于构建准确、稳定的Cox模型至关重要[4]。

本文分别使用SCAD、Adaptive Elastic Net、Adaptive Lasso和ADS惩罚方法对Cox模型进行变量选择，并使用交叉验证法进行参数调节，得到了四个模型；比较其变量选择结果和预测准确性；评估这些惩罚方法在平衡稀疏性、预测准确性、对共线性和异常值的鲁棒性、计算复杂度等方面的优劣。

1 变量选择方法及建模

1.1 变量选择方法

在医学领域的生存分析中，Cox模型是一种常用的模型，用于研究不同因素对患者生存时间的影响。为了提高模型的性能和预测准确性，除了传统的前向逐步回归和后向逐步回归，还应用了一些新的变量选择方法，如SCAD、ADS、Adaptive Lasso和Adaptive Elastic Net等。这些方法可以有效地降低模型的方差和偏差，提升模型的预测精度。

SCAD是一种基于L1范数惩罚的变量选择方法，它通过对L1范数进行平滑截断来解决Lasso方法在变量选择中存在的一些缺陷。SCAD方法的基本原理是在L1惩罚项的基础上增加一个二次惩罚项，以此在保持模型的稀疏性的同时，也能保持模型的预测准确性。在Cox模型中，SCAD方法可以用于对回归系数进行惩罚，达到变量选择的目的。相比于其他变量选择方法，SCAD方法能够有效地解决变量选择中的估计偏差和估计精度问题，因此在实际应用中广受欢迎[5-6]。

ADS（Adaptive Direction Shrinkage）是一种基于L1惩罚的变量选择方法。ADS方法的基本原理是通过对不同变量的调整方向和强度进行自适应调整，实现最优的变量选择和调整。在Cox模型中，ADS方法同样适用，可以用于对回归系数进行惩罚，以实现变量选择。相较于其他变量选择方法，ADS方法具有处理大规模数据集、高效、稳定和灵活的优点。在实际应用中，ADS方法被广泛应用于医学、金融、社会科学等领域，具有重要的理论和实践价值[5-7]。

Adaptive Elastic Net（AEN）是一种基于L1和L2范数惩罚的变量选择方法，它结合了L1和L2惩罚项，能够在保持模型的稀疏性的同时，也能保持模型的预测准确性。AEN方法的基本原理是通过自适应调整L1和L2惩罚项的权重，在不同的数据情况下实现最优的变量选择和调整，在Cox模型中同样适用。相较于其他变量选择方法，Adaptive Elastic Net方法可以同时考虑稀疏性和可解释性，能够处理变量间的相关性和噪声。该方法的特点是可以平衡不同惩罚因子的影响，具有较好的鲁棒性和预测精度，在实际中具有广泛的应用前景。

Adaptive Lasso是一种基于L1惩罚的变量选择方法，其可以自适应地调整不同变量的惩罚系数，从而实现最优的变量选择和调整。Adaptive Lasso方法的基本原理是对不同变量的惩罚系数进行自适应调整，使得影响较小的变量更容易被选择，而影响较大的变量更容易被保留。在Cox模型中，Adaptive Lasso方法同样适用，可以用于对回归系数进行惩罚，以达到变量选择的目的。相比于其他变量选择方法，Adaptive Lasso方法具有处理变量间相关性的能力，并且具有自适应性和稳健性。在实际应用中，Adaptive Lasso方法被广泛应用于生物医学、经济学和社会科学等领域，具有重要的理论和实践价值[8]。

1.2 构建模型

1.2.1 Cox比例风险模型

Cox比例风险模型的基本形式为

式（1）中，β1,β2,…,βp为自变量的偏回归系数，或者说是第j个预测因子的回归系数，它是需从样本数据作出估计的参数；X=(X1,X2,…,Xp) 是p维协变量向量；h 0(t)是当X向量为0时，h(t,X) 的基准危险率，它是有待于从样本数据作出估计的量。

式（1）可以转化为可以看出，比例风险假定各危险因素的作用不随时间的变化而变化，即不随时间的变化而变化。因此，式（1）又称为比例风险率模型（PH Model）。这一假定是建立Cox回归模型的前提条件，而且对数线性假定模型中的协变量应与对数风险比呈线性关系。其中，若Xj是非暴露组观察对象的各因素取值，Xi是暴露组观察对象的各因素取值，RR是相对危险度，即

似然比函数的值越大，说明模型的拟合程度和预测能力越好。在进行变量选择时，可以根据似然比函数的大小来评估预测因素的重要性，选择对模型性能有较大贡献的预测因素。

1.2.2 Cox-SCAD模型

Cox-SCAD模型是一种用于生存分析的统计模型，它是基于Cox比例风险模型和SCAD正则化方法的结合。Cox-SCAD模型可以用于处理高维数据集，同时能够选择重要的预测因子，减少模型的过拟合，其模型如下：

其中，pλ是SCAD惩罚函数，λ是惩罚强度，则有

1.2.3 Cox-ADS模型

Cox-ADS模型是一种用于生存分析的统计模型，它是基于加速失效时间模型（Accelerated Failure Time Model，AFT）与自适应组稀疏正则化（Adaptive Group Sparse Regularization，AGSR）的结合。ADS-Cox模型可以处理高维数据集，同时能够选择重要的预测因子，减少模型的过拟合，其模型如下：

其中，p为预测因子的数量，r为组数，λ是惩罚强度，Q是一个矩阵，mle表示最大似然估计，λωj是 Cox-ADS模型中的权重。

1.2.4 Cox-AEN模型

Cox-AEN模型是一种用于生存分析的统计模型，它是基于Cox比例风险模型和自适应弹性网络（Adaptive Elastic Net）正则化的结合。自适应弹性网络可以同时控制Lasso和Ridge惩罚的强度，因此可以更好地平衡模型的稳定性和准确性，其模型如下：

1.2.5 Cox-ALasso模型

Cox-ALasso模型是一种用于生存分析的统计模型，它是基于Cox比例风险模型与ALasso（Adaptive Lasso）正则化的结合。与传统的Lasso模型不同，自适应Lasso对于不同的预测因子可以赋予不同的惩罚系数，因此可以更好地处理高维数据集，其模型如下：

2 参数调节

参数调节是变量选择中的关键步骤，可帮助找到最优模型参数以提高准确性和性能。交叉验证是一种常用的评估模型性能的方法，将数据集分成多个子集进行训练和测试。本文采用5折和10折交叉验证法进行参数调节，结果表明使用5折交叉验证法效果更好，能更准确评估模型性能，提高泛化能力。

3 数值模拟

本文使用了基于惩罚项的变量选择方法，包括Cox-SCAD、Cox-ADS、Cox-AEN和Cox-ALasso 模型，对乳腺癌数据集进行生存分析。这些模型能够自动选择与生存时间相关的变量，降低维度并提高预测性能。此外，它们还具有Oracle性质，能够准确地识别真实的相关变量并将不相关的变量系数压缩为零，从而保证了模型的可解释性和稳定性。

该数据集包含569个样本和30个特征，是一个二分类问题。为了提高模型的训练效果，本文首先对数据进行了预处理。具体来说，使用了StandardScaler方法对数据进行标准化，将每个特征的值缩放到均值为0，标准差为1的范围内。随后将数据集划分为训练集和测试集，其中测试集占总数据集的30%，并设置随机种子为42，以保证每次运行结果的一致性。最终，得到了训练集和测试集的特征矩阵和目标向量。

在训练好的COX模型中，每个变量都会有一个对应的系数。这些系数可以用来解释变量对风险的影响。如果变量的系数为正数，表示该变量的增加与风险的增加有正相关关系；如果系数为负数，表示该变量的增加与风险的减少有负相关关系；如果系数接近于零，则说明该变量对风险的影响较小或不显著。训练结果如表1所示，这些系数可以用来进行特征选取和模型优化。

表1 系数估计值

根据表1的结果得出以下结论：

（1）在本模型中，假设变量X3和X4与其他变量存在共线性。通过使用四种基于惩罚项的变量选择方法，发现这些方法都没有将X3和X4选入模型。这说明以上四种方法都能够有效地处理共线性问题，并且能够自动选择与生存时间相关的变量，降低维度并提高预测性能。

（2）在COX模型的乳腺癌数据集中，使用不同的特征选择方法得到了不同的特征集合。具体来说，SCAD方法选择了18个特征，ADS方法选择了15个特征，Adaptive Elastic Net方法选择了25个特征，Adaptive Lasso方法选择了21个特征。这些结果说明，不同的特征选择方法会导致不同的特征集合，这可能是由于不同方法对特征的惩罚力度、结构偏好和相关性处理方式不同所导致的。

（3）在数据集中，使用Adaptive Elastic Net方法选择的特征最多，而ADS方法选择的特征最少，这可能是因为Adaptive Elastic Net方法可以保持稀疏性的同时，克服了Lasso方法在高相关性特征选择方面的一些问题，而ADS方法则没有考虑相关性。

根据表2和图1，对这四种模型进行比较，得出以下结果：

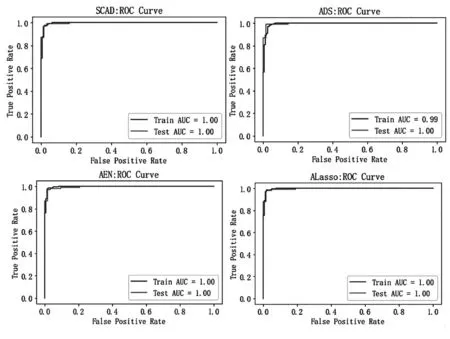
图1 四种模型的ROC Curve对比

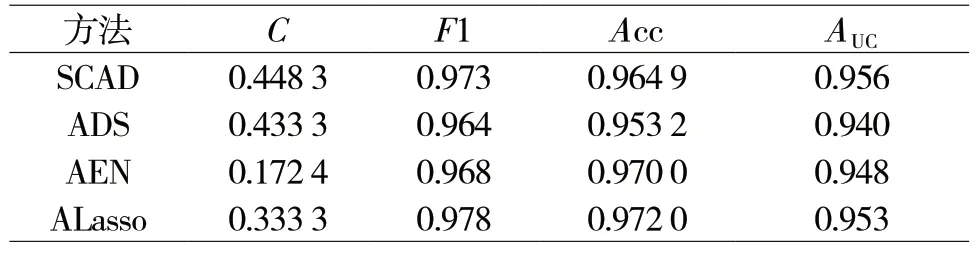
表2 四种方法不同指标的比较

（1）分类准确度（Acc）是一种常用的评估分类模型性能的指标，它的值介于0和1之间，越接近1表示模型的分类性能越好，而接近0则表示模型的分类性能较差。它提供了一个整体的性能评估指标，可以直观地了解模型对于所有类别的分类效果。这四种模型的Acc均较高，都在0.95以上。其中，AEnet方法的分类准确度最高，为0.97；其次是ALasso方法，为0.972；SCAD方法的分类准确度为0.964 9，稍低于前两者；ADS方法的分类准确度最低，为0.953 2。

（2）F1值是精确率（Precision）和召回率（Recall）的调和平均数，它综合衡量了分类器的准确性和覆盖能力。F1值在0到1之间，越接近1则表示分类器性能越好。它在处理类别不平衡问题时尤为重要，因为此时单一指标（如准确率）可能无法全面反映模型性能。F1值提供了一个综合指标，帮助评估分类器在精确率和召回率之间的权衡。表2中，四种模型的F1值均较高，其中ALasso方法的F1值最高，为0.978；其次是SCAD方法，为0.973；AEnet方法的F1值为0.968，略低于前两者；ADS方法的F1值最低，为0.964。

（3）ROC曲线是以真正例率（True Positive Rate，TPR）为纵轴，假正例率（False Positive Rate，FPR）为横轴，绘制的一条曲线。它可以帮助我们理解模型在不同阈值下的分类结果，以及灵敏度和特异度之间的权衡。这四种模型的ROC曲线下的面积（AUC）也都较高，均在0.94以上。其中，SCAD方法的AUC最高，为0.956；其次是ALasso方法，为0.953；AEnet方法的AUC为0.948，略低于前两者；ADS方法的AUC最低，为0.940。

（4）惩罚系数（C）值，用于控制模型对错误分类的惩罚程度和权衡损失函数与正则项的关系。合适的C值可以平衡模型的复杂度与容错能力，降低过拟合和欠拟合风险。选择最优C值是一个重要的调参过程，通常通过交叉验证等方法来实现。其中，AEN方法的惩罚系数最小，为0.172 4；其次是ALasso方法，为0.333 3；SCAD方法的惩罚系数为0.448 3，略高于前两者；ADS方法的惩罚系数最大，为0.433 3。

综合来看，这四种模型在分类准确度、F1值和AUC指标上表现都较好，但各有优劣。ALasso方法在分类准确度、F1值和AUC指标上表现良好，且惩罚系数较小；SCAD方法在AUC指标和F1值上表现较好，但惩罚系数较大；AEN方法在分类准确度、F1值和惩罚系数指标上表现最好；ADS方法在分类准确度和AUC指标上表现略低，但惩罚系数最大。

4 结论

本文通过对Cox比例风险模型中的多种变量选择方法的比较与应用研究，得出了以下结论：这四种方法都能够有效地处理共线性问题，并且能够自动选择与生存时间相关的变量，降低维度并提高预测性能。不同的特征选择方法会导致不同的特征集合，这可能是由于不同方法对特征的惩罚力度、结构偏好和相关性处理方式不同所导致的。其中，Adaptive Elastic Net方法选择的特征最多，而ADS方法选择的特征最少，这可能是因为Adaptive Elastic Net方法可以保持稀疏性的同时，克服了Lasso方法在高相关性特征选择方面的一些问题，而ADS方法则没有考虑相关性。在分类性能方面，这四种模型在分类准确度、F1值和AUC指标上表现相似，但是在预测阳性患者的召回率上，Adaptive Elastic Net方法表现最好，这说明在生存分析中，Adaptive Elastic Net方法可能更适合于对阳性患者进行筛查和预测。

综上所述，这四种基于惩罚项的变量选择方法可以有效地处理生存分析中的高维数据和共线性问题，提高预测性能和可解释性，但它们在选择特征和分类性能方面存在一定的差异，需要根据具体问题选择合适的方法。