直联式隧道通风机机械传动过程瞬态振动控制

姚 宇，方忠强

（华设设计集团股份有限公司 水下隧道智能设计、建造与养护技术与装备交通运输行业研发中心，南京 210014）

随着城市交通建设的推进，隧道挖掘工程也取得了高速的发展。直联式隧道通风机是服务于隧道挖掘工作的重要设备[1-2]，其工作过程中，通风机机械传动过程极易出现瞬态振动问题，从而影响直联式隧道通风机的正常运行。

为此，文献[3]通过磁流变弹体分析海上风机的工作原理，建立海上风机动力学模型，通过调谐质量阻尼器完成风机的传动控制。文献[4]中首先建立了传动系统动力学模型，然后分析系统固有振动特性，最后通过主从扭矩控制方法完成风机传动机械振动控制。文献[5]中首先通过流体动力特性建立模型，然后通过静态特性对噪声实行抑制，最后，完成对风机传动机械振动控制。但是在实际应用中发现，上述传统控制方法的控制效果还有很大的提升空间，在减小振动加速度等方面的效果仍不理想。

为了解决上述方法中存在的问题，本研究提出直联式隧道通风机机械传动过程瞬态振动控制。

1 构建直联式隧道通风机机械传动模型

本研究利用拉格朗日方程建立直联式隧道通风机机械传动系统的动力学模型。

直联式隧道通风机装置如图1（a）所示，其传动结构如图1（b）所示。直联式隧道通风机转速通常在一阶临界转速内，故可通过刚性系统描述通风机转子系统，其简化示意图如图1（c）所示。

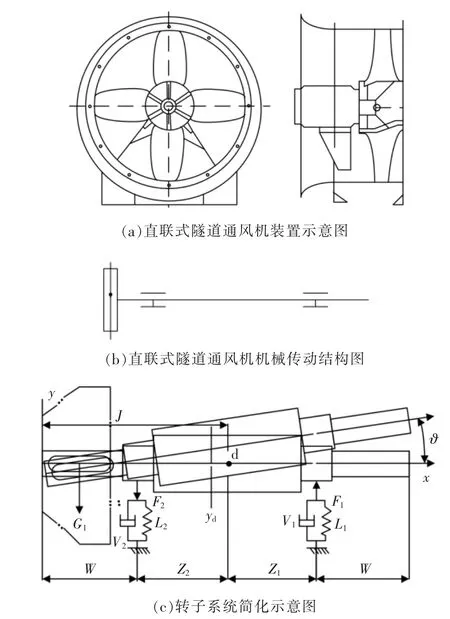
图1 直联式隧道通风机机械传动系统示意图Fig.1 Schematic diagram of mechanical transmission system for directly connected tunnel ventilation fan

图1 中，d 表示转子质心，yd表示质心位移，ϑ表示质心移动转角，J 表示转动惯量，l1、l2表示转子支撑刚度系数，G1表示叶轮重力，F1、F2表示支撑弹性力，Z1、Z2表示质心到支撑力距离，V1、V2表示转子支撑阻尼。

拉格朗日方程动力学公式表达如下：

式中：Wo表示第o 个广义坐标的广义力；R 表示系统动能；I 表示系统势能；wo表示第o 个广义坐标。

将支撑通风机主轴的两个弹性力看做外力，根据式（1），进一步推导出如下公式：

直联式隧道通风机机械传动系统动力学的广义坐标取质心转动度数ϑ 和质心位移yd，即q1=ϑ、q2=yd，推导出直联式隧道通风机机械传动系统动能R：

式中：Mp表示直联式隧道通风机主轴质量；Jd表示转动惯量。

进一步推导出直联式隧道通风机主轴支撑的两个弹性力F1、F2公式表达如下：

式中：l1、l2表示转子支撑刚度系数；Z1、Z2表示质心到支撑力距离[6-7]。

根据图1（c）中直联式隧道通风机转子系统示意图可知，通风机主轴在转动时受到不平衡量影响，用Wmt表示，计算通风机主轴的不平衡力Fu公式表达如下：

式中：α 表示通风机主轴转动角速度。

进一步推导出直联式隧道通风机机械传动系统动力学方程，其公式表达如下：

式中：t 表示时间。

将上述求得的直联式隧道通风机主轴支撑弹性力F1、F2和主轴受到的不平衡力带入到式（6），推导出直联式隧道通风机机械传动系统动力学公式表达如下：

因支撑主轴的两转子呈对称状态，故两支撑阻尼和刚度系数相等，即V1=V2、Z1=Z2。

2 线性FxLMS 算法

根据直联式隧道通风机机械传动系统动力学模型，使用线性FxLMS 算法实现直联式隧道通风机机械传动过程瞬态振动控制[8]。

FxLMS 算法是一种通过噪声抑制优化的最小均方算法，具有环境适应性强、方便实现、精度的误差鲁棒性好等优点。其控制系统如图2 所示。

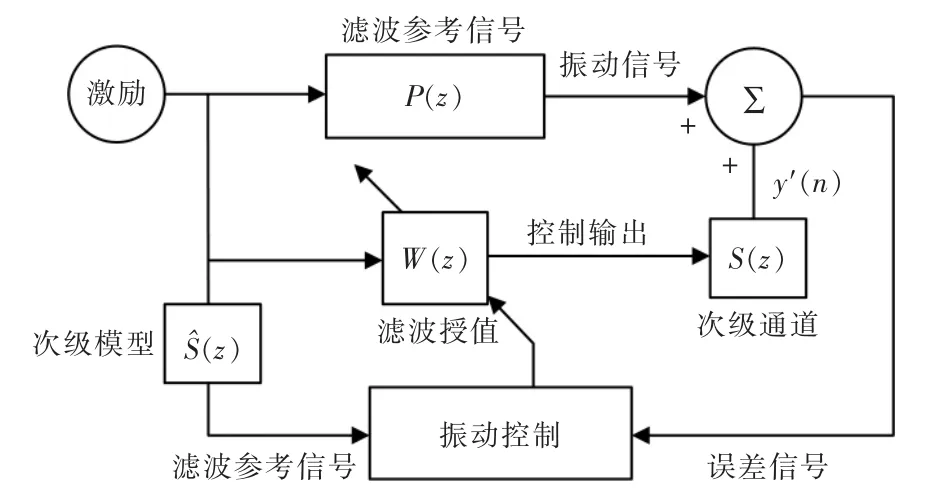
图2 线性FxLMS 算法控制Fig.2 Linear FxLMS algorithm control

引入滤波器对输入信号实行滤波处理，以保证FxLMS 算法的收敛性，控制器由控制信号输出和滤波器权值更新两部分组成。

当控制器次级通道处于理想状态时，用n 表示时间序列，原始信号与控制器反振动信号产生的传感器测量残余信号r（n）公式表达如下：

式中：f（n）表示振动源信号；u′（n）表示反振动信号；X（n）表示误差信号变量。

由此推导出E（n）公式表达如下：

式中：e 表示矩阵内的元素；n＝（0，1，2，…，l-1），表示第n 个向量。

参考信号量C（n）公式表达如下：

式中：Z 表示滤波器长度。

对次级通道实行滤波处理以消除次级通道的影响以确保LMS 算法的收敛性，滤波参考信号x′（n）公式表达如下：

通过最小均方值的最速下降法推导出控制滤波器的权值系数梯度下降算法W（n+1）公式表达如下：

式中：ν 表示迭代步长，影响控制器的收敛度及控制稳定性能；x′（n）表示参考信号。

进一步推导出滤波参考信号x′（n）公式表达如下：

基于此，通过线性FxLMS 算法完成通风机机械传动振动控制。

3 利用改进线性FxLMS 算法控制瞬态振动

由于线性FxLMS 算法在振动控制应用中受到野值、冲击噪声等干扰影响系统的稳定性，故通过跟踪滤波器和非线性变换函数对输入信号和误差信号实行优化处理，并通过新的准则更新优化FxLMS算法，完成最终的直联式隧道通风机机械传动瞬态振动控制[9-10]。

改进FxLMS 算法结构如图3 所示。

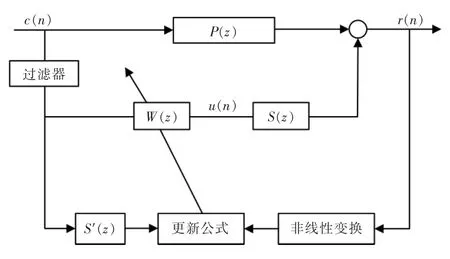
图3 改进FxLMS 算法结构Fig.3 Improved structure of FxLMS algorithm

跟踪（TD）滤波器用于剔除野值和消除噪声的跟踪微分器。假设c1（n）、c2（n）表示滤波器输出信号，c1（n）表示跟踪输入信号，c2（n）表示微分信号，跟踪滤波器公式表达如下：

式中：c（n）表示输入参考信号；j 表示步长；t、jo表示参数。增大时间参数t，可加快滤波器的速度，参数jo的最佳选择可获取滤波器的最佳性能，从而通过滤波器实现噪声去除。

误差信号同样影响初级通道信号更新的稳定性，故通过变换函数Γ（r（n））消除误差信号中的干扰，用μ 表示设定误差阈值，其公式表达如下：

式中：r（n）表示误差信号；l 表示可以决定消减速度的参数。

当误差小于等于设定误差阈值时，保持误差信号不变，当误差大于设定误差阈值时，则消减参考信号。

使用新的优化准则更新滤波器权值，其公式表达如下：

式中：σ 表示迭代步长；w（n）表示滤波器系数。

FxLMS 算法改进步骤如下：

步骤1：初始化滤波器参数t、jo、μ、l、w（n）；

步骤2：通过式（14）获取FxLMS 算法参考输入信号；

步骤3：通过式（15）对误差信号进行处理；

步骤4：通过式（16）更新FxLMS 算法滤波器系数；

步骤5：返回步骤（2），获取最终输入信号。

基于此，完成最终的直联式隧道通风机机械传动过程瞬态振动控制。

4 实验与分析

为了验证直联式隧道通风机机械传动过程瞬态振动控制方法的有效性，对其完成如下测试。

在Intel Corel i7-12700KF CPU、32 GB RAM、2.11 GHz 配置的计算机上使用bladed 软件，建立直联式隧道通风机机械传动系统。

为避免测试结果较为单一，将文献[3]方法、文献[4]方法作为对比，从风筒顶层位移响应时程、振动加速度幅值以及减震率3 个角度，与所提方法共同完成性能对比验证。

4.1 风筒顶层位移响应时程

采用所提方法、文献[3]方法、文献[4]方法完成直联式隧道通风机机械传动过程瞬态振动控制，其风筒顶层位移响应时程对比结果如图4 所示。

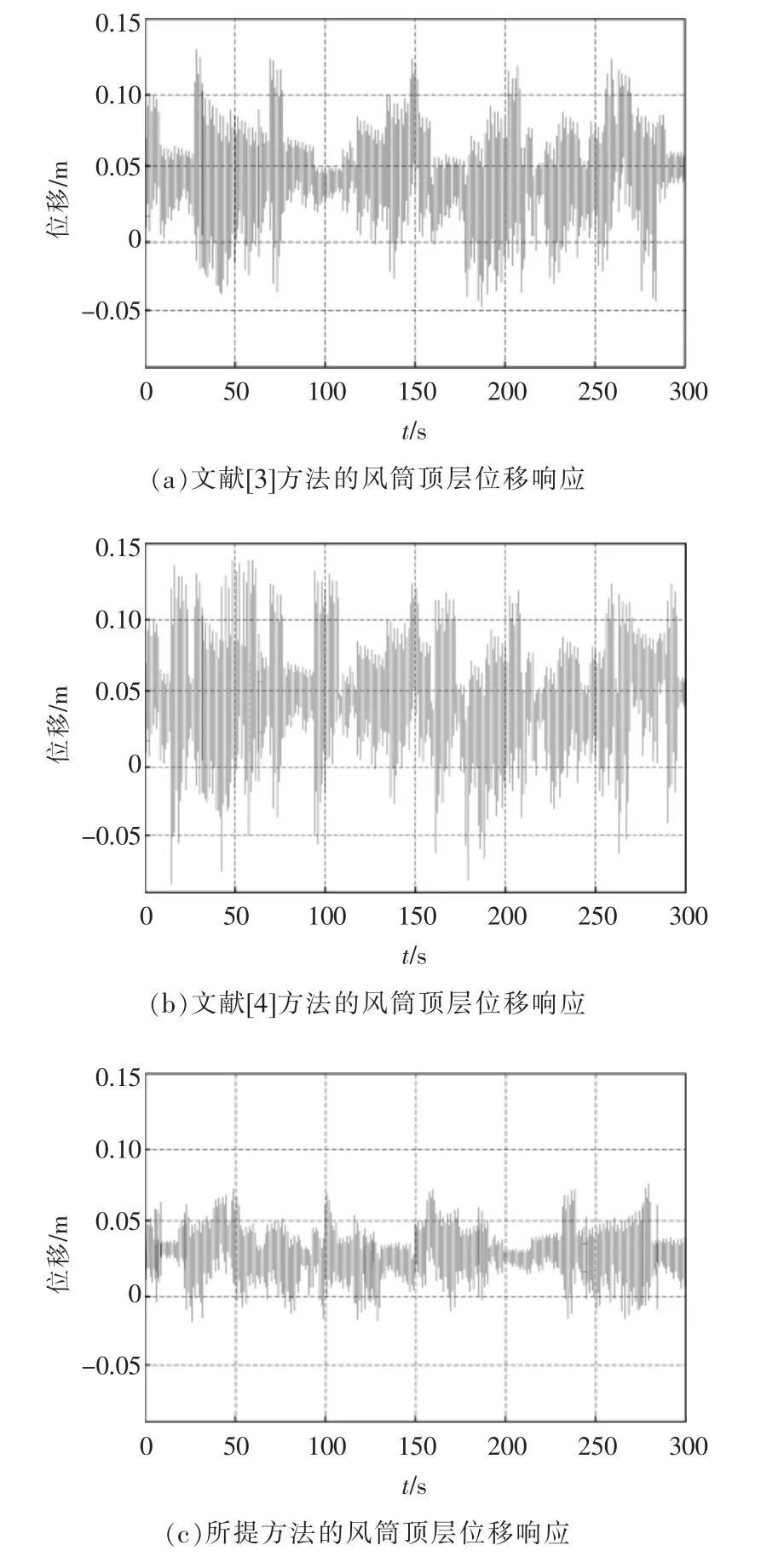
图4 三种方法的风筒顶层位移响应结果对比Fig.4 Comparison of displacement response results of the top layer of the air duct using three methods

分析图4 所示结果可知，相较于文献[3]方法、文献[4]方法，应用所提方法后，风筒顶层位移响应较小。位移响应值越小，振动控制效果越好，由此可以表明，所提方法对风机机械传动的控制效果更好。

4.2 加速度幅值

采用所提方法、文献[3]方法、文献[4]方法完成直联式隧道通风机机械传动过程瞬态振动控制，其加速度幅值对比结果如图5 所示。

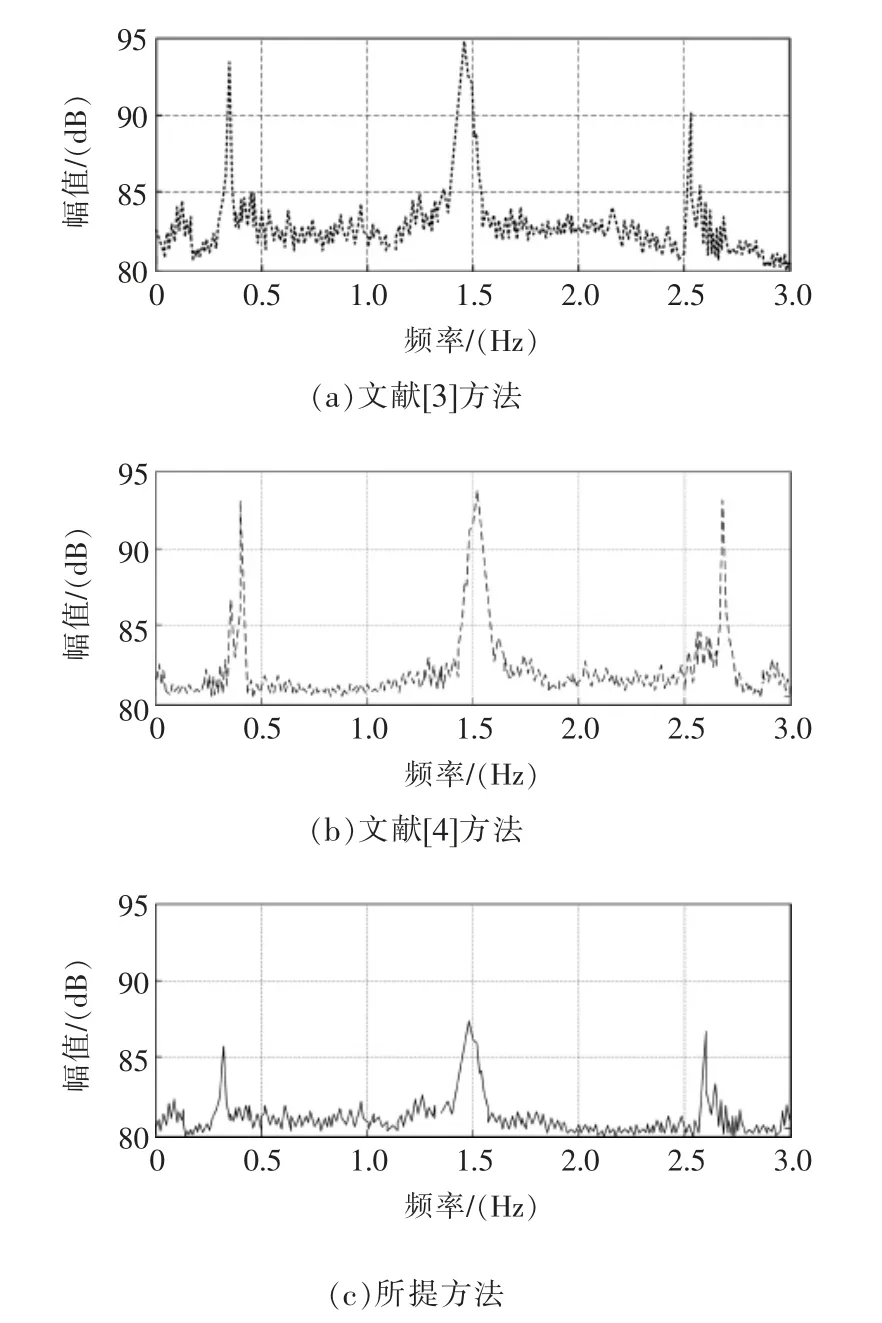
图5 三种方法的振动加速度幅值Fig.5 Vibration acceleration amplitude of three methods

分析图5 所示结果可知，采用所提方法后，通风机振动加速度幅值远低于文献[3]方法和文献[4]方法。振动加速度幅值越小，代表控制效果越高，由此可以表明，所提方法对瞬态振动的控制效果更好。

4.3 减振率

采用所提方法、文献[3]方法、文献[4]方法完成直联式隧道通风机机械传动过程瞬态振动控制，其减振率如表1 所示。

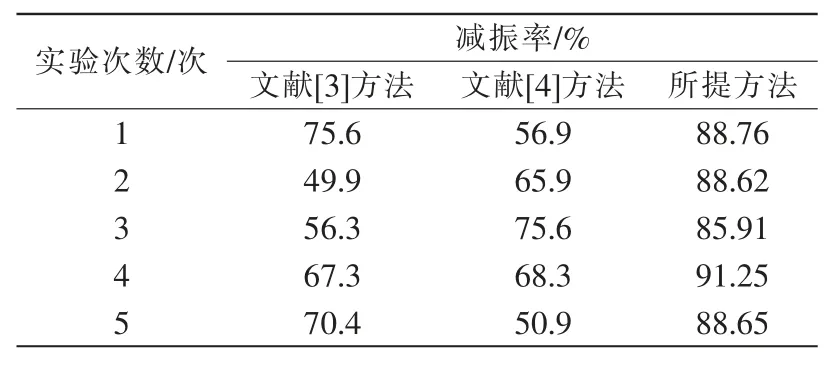
表1 三种方法的减振率Tab.1 Damping rate of three methods

分析表1 所示结果可知，所提方法的减振率始终高于文献[3]方法和文献[4]方法，始终保持在85%以上。减振率越大，表明控制稳定效果越好，由此可以表明，所提方法的控制稳定性更好。

通过上述实验可知，所提方法基于线性FxLMS算法的通风机机械传动振动控制，提高了通风机传动振动控制的效率，通过对线性FxLMS 算法的优化，提高了振动控制稳定性，获得了更好的通风机机械传动过程瞬态振动控制效果。

5 结语

直联式隧道通风机是用于隧道挖掘工作的重要工具之一，其传动系统振动控制是直联式隧道通风机正常工作的保障。目前的传动振动控制存在稳定性不佳等问题，因此，本研究提出了直联式隧道通风机机械传动过程瞬态振动控制方法。首先，建立通风机机械传动系统动力学模型，然后在初步控制的基础上，通过优化线性FxLMS 算法实现精准控制。该方法解决了传统方法中存在的问题，具有重要的现实应用意义。