圆形巷道围岩破坏机制解析及静动耦合响应力学行为

岳鹏威, 王继兵, 魏晓刚

(郑州航空工业管理学院土木建筑学院, 郑州 450046)

随着煤炭资源的开采,浅层的煤炭资源日益匮乏。为了满足高速的社会经济的发展,煤炭资源的开采逐渐向深部地下转移。然而,深部开采面临诸多问题,其中巷道围岩受到“三高一扰动”的影响,极易出现围岩变形大和破裂范围广等现象[1-3]。相关研究发现,围岩塑性区的逐步形成是导致围岩破坏的诱导因素,塑性区的形态和形成范围决定了巷道围岩的破坏程度[4]。在巷道开挖过程中,常遇到诸如地震、爆炸等动态载荷的作用,这些动态载荷作用会对塑性区形态和范围产生影响。因此,静动耦合作用下围岩塑性区以及力学响应是目前研究的热点。

关于巷道围岩塑性区理论,学者们利用Mohr-Coulomb、Hoek-Brown和Drucker-Prager等准则对塑性区的问题已经开展相关研究[5-7]。王卫军等[8-9]基于Mohr-Coulomb强度准则,研究了非等压圆形巷道围岩塑性区边界方程的近似解,并通过理论分析和数值模拟方法对围岩塑性区的形成和发展进行探究。朱影等[10]通过现场监测和数值模拟手段分析了围岩在采动过程中塑性区的变化,结果发现塑性区均小于工作面后方,且与巷道围岩的位移量有很好的一致性。赵洪宝等[11]利用理论分析和数值模拟方法对不同侧压力系数下的巷道围岩应力分布进行分析,同时进一步对围岩的塑性区和稳定性进行探究。王永红等[12]基于广义张-朱强度(generalized Zhang-Zhu strength criterion, GZZ)准则对深埋隧道的围岩塑性以及变形展开分析,结果发现,采用GZZ强度准则,围岩的塑性半径显著减小,应力逐渐增大。孙中华等[13]通过非线性解析方式对考虑地下渗流情况下围岩的应力场以及塑性区的半径展开理论研究。尹光志等[14-15]基于平面应变理论,研究了不同钻孔半径下的围岩塑性区特性,并分析了中间主应力对塑性区范围的影响。郭晓菲等[16]发现圆形巷道在不同的围压状态下表现出圆形、椭圆形和蝶形状态,并通过塑性区边界隐形方程判别塑性区形态特征。

上述研究主要针对单一静态载荷作用下巷道围岩塑性区,然而针对动静耦合下围岩塑性区的变化规律以及破坏特征尚不明晰。实际工程围岩多受采动应力、地应力等多场静动荷载耦合作用,围岩变形破坏问题突出,给工程活动的安全进行带来极大威胁。因此,现首先利用理论分析的方法探究围岩塑性区变化规律,基于ANSYS数值模拟平台对不同侧压工况下围岩应力场分布特征进行分析,定量分析侧压系数对围岩不均匀变形行为的影响,探究静动耦合作用下围岩力学响应行为特征。

1 理论分析

1.1 围岩应力场分布解析

巷道围岩破坏与围岩的应力状态密切相关。由于巷道围岩的应力状态的复杂性和多变性,目前针对围岩受力状态的分析基于多种本构关系下进行的,很难利用统一的本构关系进行分析。建立的巷道围岩力学模型如图1所示。

pk为水平方向应力;Rp为塑性区半径图1 巷道围岩力学模型Fig.1 Mechanical model of surrounding rock of roadway

针对巷道围岩塑性区的分析至今没有给出精确的解析解。目前,中外学者仍根据弹性理论来求解弹塑性边界线[8]。在巷道的非等压应力场中,围岩上任意一点的径向应力、切向应力和剪切应力分别[17]为

(1)

我国婚姻法保护婚姻关系，保障一夫一妻制的家庭结构遭受挑战、“第三人”理应为其非理性行为承担相应的责任。无权利则无救济，第三人干扰婚姻关系使得无过错配偶遭受侵权，无过错配偶诉请“第三人”以法律责任。第三人干扰婚姻关系是侵权行为，同样也应当存在被侵权的客体一配偶权。

(2)

(1-k)sin2θ

(3)

式中:r为围岩上一单元到巷道圆心间的距离;R0为巷道半径;σr为径向应力;σθ为切向应力;τrθ为剪切应力;k为侧压力系数;θ为围岩上单元与水平方向的夹角;p为竖直方向应力。

假设巷道围岩是连续的过渡到理想塑性状态,且围岩破坏遵循Mohr-Coulomb准则。图2为最大剪应力准则示意图。根据内摩擦角φ和黏聚力c,求得塑性条件为

图2 最大剪应力准则示意图Fig.2 Schematic diagram of maximum shear stress criterion

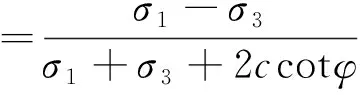
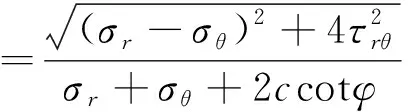
(4)

式(4)中:σ1、σ3分别为最大、最小主应力。

联立式(1)～式(3)代入式(4)中,可以得到非等压圆形巷道围岩塑性区边界方程[8]为

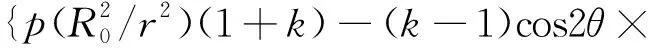
-4c2}(1-cos2φ)/2-4c2-2csin2φ×

(5)

当f(r,θ)=0时,式(5)表示的是巷道围岩塑性区边界方程。

1.2 围岩塑性区分布特征

为了研究不同侧压系数k[18]对巷道围岩塑性区范围的影响,根据实际工况的条件,将压力p=15 MPa、巷道半径R0=1 m、黏聚力c=4 MPa和摩擦角φ=24°代入式(5),得到不同侧压系数k下围岩塑性区的分布特征,并将不同侧压系数k下的围岩塑性分布区绘制在图3中。

图3 不同侧压系数下的围岩塑性分布区Fig.3 Plastic distribution zone of surrounding rock under different lateral pressure coefficients

从图3中可以发现,在侧压系数k=1时,巷道围岩塑性区与巷道圆形呈近似同心圆分布,同心圆的半径大约为1.4 m。随着侧压系数k的逐渐增大,塑性区范围从圆形分布逐渐变为椭圆形分布,并最终变为“蝶形”分布。巷道顶板塑性区的半径随着侧压系数k增加而逐渐增加,但两帮塑性区半径随着侧压系数的增加而减小。侧压系数k的增加会造成巷道两肩角相对圆形巷道有突出现象。且侧压系数k越大,两肩角突出现象越显著。

2 静动耦合数值模拟

2.1 数值模拟方案

横断山区东北部某矿区,地表高差较大,地表土层薄。矿区某工作面倾斜长108.0～198.6 m,平均走向长200～290 m,回采面积约6.5×104m2,开采区域内可采煤层累计厚度6 m,煤层埋深350～410 m,处于16号向斜两翼;其中,32、33-1、36号煤层已部分回采,待采工作面7363位于井田+1220水平七采区+1230～1286区段,此区段赋存围岩岩性以砂岩、砂砾岩、泥岩为主,分级为中等偏硬岩,煤层倾角16°～23°[19]。围岩受自重应力、构造应力影响较为明显,开采过程中,在采动应力、地应力场的耦合作用下,围岩稳定性控制是重要的问题。

在巷道开挖工程中,ANSYS软件作为一个比较成熟的数值模拟平台被广泛地应用到巷道围岩变形破坏分析上。利用ANSYS平台建立的巷道数值模型如图4所示。岩体的数值模型尺寸为10 m×10 m,在岩体上开挖直径为1 m的巷道,并沿着轴向方向取一延米进行计算。巷道的单元为三维实体单元,网格单元总数为614 304个,网格划分尺寸为20 mm,网格划分方法为映射划分。施加初始竖直方向应力场40 MPa和水平方向应力场,其中巷道的侧压系数分别设置为1、1.25、1.5、1.75、2和2.25;然后使用dynian文件法,施加正弦应力波动态荷载作用,其实现方法是通过*DEFINE_CURVE_TITLE命令将动态荷载施加到已承受静力作用后的模型,从而实现静动耦合荷载作用。模型四周设置约束边界。计算步长为100 μs,整个静动耦合响应过程通过75个步长来实现。岩体的计算模型采用HJC模型(*MAT_JOHNSON_HOLMQUIST_CONCRETE),详细参数如表1[20]所示。

表1 围岩物理性能参数表Table 1 Physical property parameters of surrounding rock

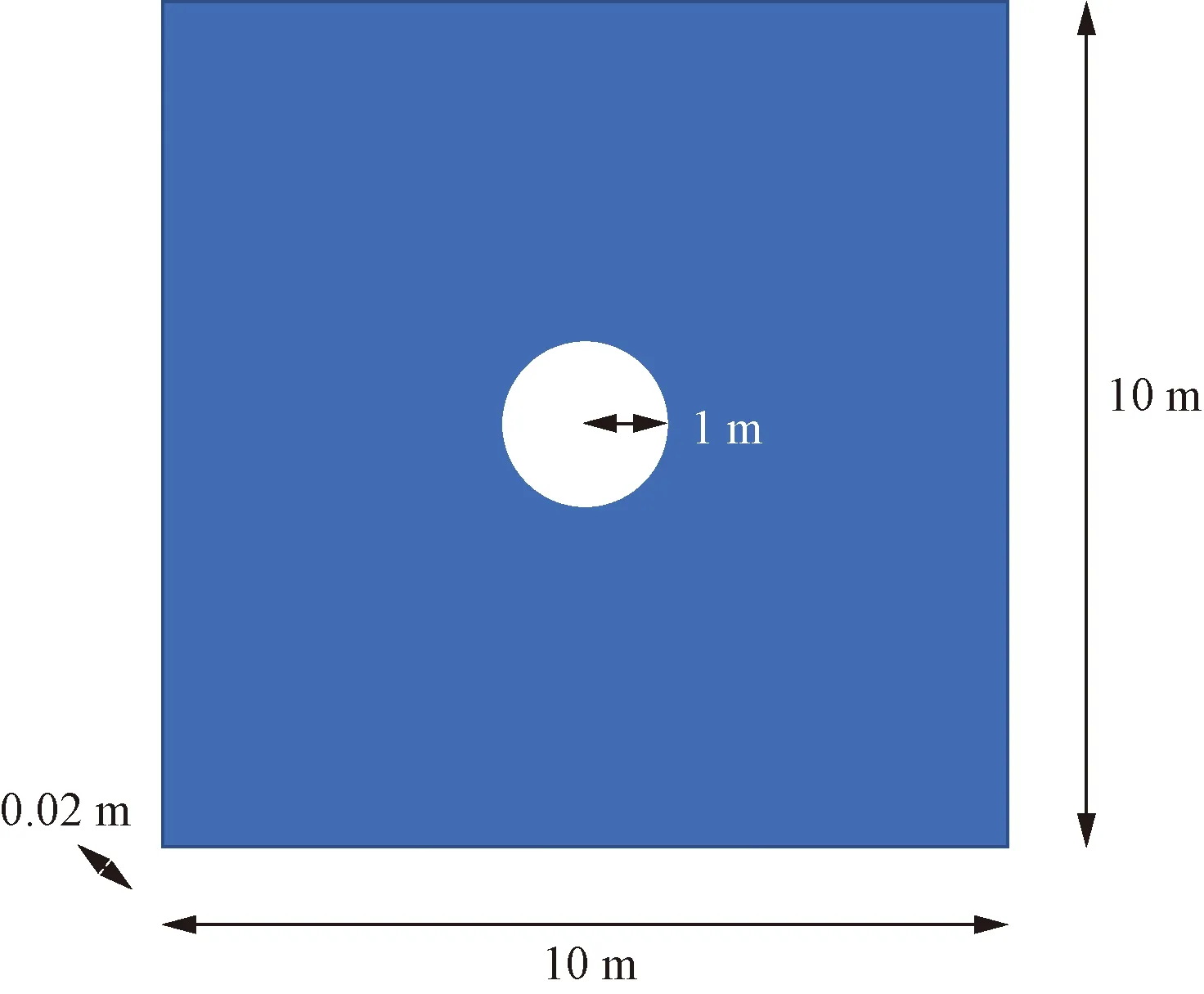
图4 巷道数值模型示意图Fig.4 Schematic diagram of numerical model of roadway

2.2 静动耦合响应分析

2.2.1 静态荷载作用时围岩力学行为

静态荷载下的有效应力云图如图5所示。当侧压系数k=1时,有效应力云图沿着巷道周边呈明显的圆形分布。有效应力的峰值在图5(a)中围成闭合的圆形,最大值为30.62 MPa;当k=1.25时,有效应力云图变成巷道顶部凸起而两帮略向内凹陷,沿着巷道周边呈椭圆形分布,塑性区形态为椭圆形。值得注意的是有效应力峰值沿着巷道不再是闭合的椭圆形分布,在巷道上顶面和下地面呈月牙形,最大值为35.20 MPa;当k分别为1.5、1.75和2.0时,巷道两帮有效应力分布向内凹陷程度逐渐加剧,上顶面和下顶面凸起愈加明显,有效应力最大值分别为47.01、52.84、61.57 MPa;当k=2.25时,有效应力云图在巷道两侧出现明显的肩角现象,呈现出蝶形分布,这与塑性区分布区域吻合。以上分析可得,侧压力系数的增加,导致有效应力分布发生明显的变化。有效应力峰值随着侧压力系数的增大逐渐增大。6组不同侧压力系数下的有效应力分布区域与塑性区的理论计算值有一定的吻合性。

图5 静态荷载下作用巷道围岩有效应力云图Fig.5 Effective stress cloud diagram of roadway surrounding rock under static load

不同侧压力系数下有效应力变化如图6所示,分别取距离巷道中心的距离r=1.0、1.5、2.0和2.5处的有效应力进行分析。从图6可以发现,当k=1时,相同距离处的有效应力值基本相同,呈类圆形分布,有效应力随着r增大呈逐渐减小的趋势。当k=1.25时,r=1.0处的有效应力最大值明显增大,但其他区域的有效应力最大值无明显变化的趋势,有效应力在整体上呈椭圆形分布。当k=1.5时,距离巷道中心不同位置处的有效应力最大值相对于k=1.25情况无明显变化,但在r=1.0处的巷道两帮的有效应力值相对其他巷道部位较小。当k=1.75、2.0和2.25时,半径r=1.0处的有效应力最大值基本相等,但同一侧压力系数下的巷道两帮处围岩有效应力相对其他部分减小程度较大。对比不同侧压力系数下r=1.5、2.0和2.5处的有效应力变化,有效应力随着侧压力系数的增大有明显的增大趋势,且两帮处的有效应力值也会受到明显影响。综上分析可知,较小的侧压力系数(1≤k≤1.25)对距离巷道较近(r=1.0)的围岩区域产生显著影响,但对距离巷道较远(r>1.0)的区域无明显影响;相反,较大的侧压力系数(k>1.25),对距离巷道较远(r>1.0)的围岩区域产生显著影响,但对距离巷道较近(r=1.0)的区域无明显影响。

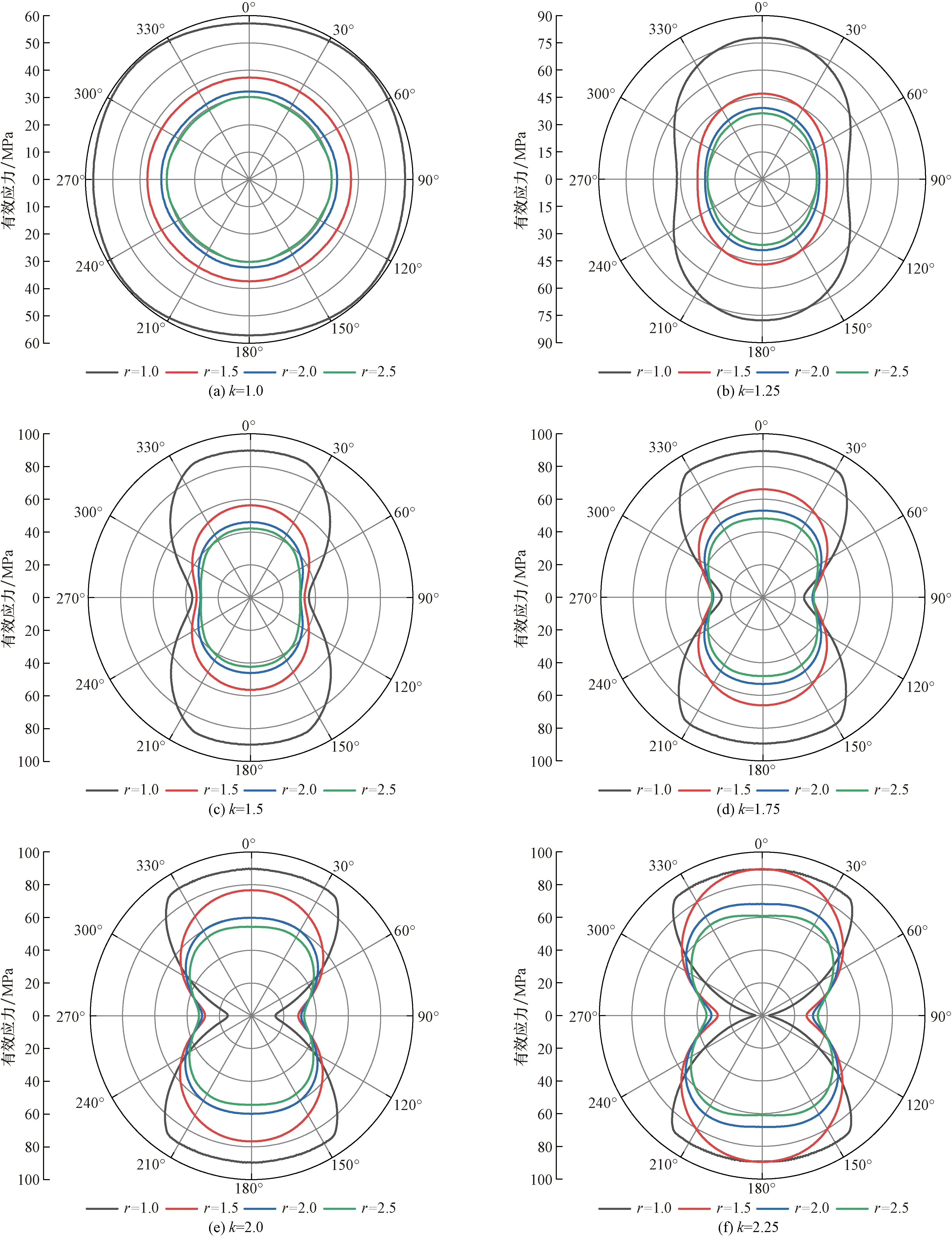
图6 不同侧压系数围岩有效应力变化Fig.6 Variation of effective stress of surrounding rock with different lateral pressure coefficients

2.2.2 围岩位移变化

围岩相对于巷道中心的位移如图7所示。由图7可知,侧压系数k=1.0时,即巷道承受等压应力场作用时,巷道围岩在应力作用下发生的位移值大小不随方位的变化而变化。当承受非等压应力场作用时,巷道围岩的变形呈现较大的变化。围岩不同方位处的位移值所形成的包络线由k=1.0时的圆形分布变化为k=1.25、1.50、1.75、2.0、2.25的非圆形分布。此时,在非等压应力场作用下,围岩位移值包络线由k=1.25类椭圆逐渐过渡到k=2.25的双圆形分布。这表明,在不同侧压系数的应力场作用时,巷道围岩的变形情况具有显著的差异性。随着侧压系数的增大,围岩发生较大的非均匀性变形,由此伴生的围岩内部应力集中程度加剧、应变能高水平集聚等结果将对围岩的稳定性带来明显影响。这尤其表现在实际非等压应力场赋存巷道中,围岩由于局部大变形破坏而诱发动力灾害,如围岩左右帮的片帮、顶底板的冒顶底鼓等事故的发生。

图7 围岩与巷道中心的相对位移Fig.7 Relative displacement of surrounding rock and roadway center

不同侧压系数下,巷道围岩左右帮、顶底板位移如图8所示。k=1.0时,由于围岩在不同方位发生相同程度变形,因此位移值相同。随着侧压系数增大,巷道左右帮及顶底板位移呈现差异化的变化趋势,其中,左右帮围岩发生的位移值呈现较大的增长,k=2.25时,左右帮的位移达到13.5 mm,顶底板的位移值相对于左右帮而言越来越小。由于侧压系数的增大,巷道围岩承受非等压应力场作用,顶底板受到一定的夹制作用,围岩承受以压应力为主导的应力场作用,在左右帮,则以拉应力为主导的应力场作用下发生较大位移。

图8 围岩位移与侧压系数的关系Fig.8 Relationship between surrounding rock displacement and lateral pressure coefficient

2.2.3 围岩静动耦合力学响应分析

静动荷载下围岩的破坏区域如图9所示。从图9中可以发现,当k=1时,围岩的破坏区域呈圆环分布;当k=1.25时,围岩两帮的破坏区域向巷道内略有凹陷,整个破坏区域近似椭圆形;当k=1.5时,由于侧向压力增大,巷道围岩两帮附近的破坏区域明显变窄,但围岩顶板和底板破坏区域明显变宽。随着侧压力系数的进一步增大(k=1.75和2.0),围岩的破坏区域分布也不尽相同,整体上顶板和底板附近的破坏面积显著大于两帮围岩的破坏面积。当k=2.25时,巷道两侧出现肩角破坏现象,且两帮围岩破坏区域明显缩小。

图9 静动荷载下围岩破坏区域Fig.9 Failure area of surrounding rock under static and dynamic load

巷道围岩在静态应力场作用下,形成以图5所示的不同特征的应力场分布情况,此时在承受动态荷载的作用后,围岩将在静动荷载耦合作用下发生如图9所示的失效破坏现象。具体到实际工况中的冲击地压诱发冒顶、片帮等围岩失稳动力灾害事故而言,围岩往往由于承受长期静力场的作用积累一定的弹性能,在动态扰动时,便极易无序性、随机性的释放。

在静动耦合应力场作用时,围岩内部的应力分布较为复杂,但根据经典的岩石力学理论而言,围岩的最终破坏由破坏面形成初期的剪应力主导,在等压应力场作用时,围岩中的最大剪应力[8]为

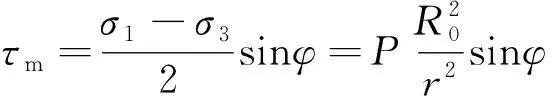
(6)

由此可知,围岩中的最大剪应力的等值包络线与巷道同圆心分布,因此,围岩的破坏区域呈现圆环状分布。

当围岩承受非等压应力场作用时,围岩中的最大剪应力超过极限剪应力时,可形成塑性破坏区,此时的破坏范围为

(7)

式(7)中:ξ为围岩形成的破裂面与最大主应力之间的夹角;α为破坏边界取极限平衡状态时的屈服点方向的夹角,其值与岩性及应力状态有关。

因此可知,当围岩承受非等压应力场作用时,围岩的破坏将可能首先在角度为π/4+φ/2所在的面发生,形成图9中不同形状的破坏区域。

3 结论

(1)基于Mohr-Coulomb破坏准则计算得到的塑性区的边界方程对围岩破坏机制研究有一定的参考价值。不同侧压工况下,围岩破坏区域理论解对工程活动中围岩稳定性控制分析与支护方案设计等问题有一定的指导作用。

(2)侧压系数对静态荷载下的有效应力分布影响显著,有效应力分布与塑性区的边界方程有很强的吻合性。较小的侧压系数(1≤k≤1.25)对距离巷道较近(r=1.0)的围岩区域产生显著影响,但对距离巷道较远(r>1.0)的区域无明显影响;相反,较大的侧压系数(k>1.25),对距离巷道较远(r>1.0)的围岩区域产生显著影响,但对距离巷道较近(r=1.0)的区域无明显影响。

(3)在不同侧压系数的应力场作用时,巷道围岩的变形情况具有显著的差异性。随着侧压系数的增大,围岩发生较大的非均匀性变形。巷道顶板和底板的位移随着侧压系数的增大呈逐渐减小的趋势。然而,巷道左右两帮的位移随着侧压系数的增大逐渐增大。

(4)在静动耦合作用下,随着侧压系数的增大,顶板和底板的围岩破坏区域显著增加,但两帮围岩的破坏面积有减小的趋势,破坏区域由圆形分布过渡到非规则形态。