高速飞行器集群通信拓扑自适应控制方法

白成超，王会霞，郭继峰，路坤锋

(1. 哈尔滨工业大学航天学院，哈尔滨 150001；2. 北京航天自动控制研究所，北京 100854；3. 宇航智能控制技术国家级重点实验室，北京 100854)

0 引 言

近年来,随着高速无人飞行器技术的快速发展,高速飞行器集群已经成为了一种重要的协同任务执行平台。高速飞行器集群具有许多优点,如大规模、多功能、高灵活性、低成本等[1],这使得高速飞行器集群在协同搜索、协同抗干扰和协同打击等领域得到了广泛的应用[2]。

在高速飞行器集群执行协同任务时,通信是集群的基础之一。集群飞行器之间的通信可以实现状态和载荷信息的交换,提高协同任务的效率和可靠性。然而,由于飞行器集群的特殊性,其具有大规模、多任务、速度快、时空关系变化频繁和信息传递即时突发等特点[3],这些特点为集群通信的稳定性和鲁棒性带来了较大的挑战性。通信拓扑结构是指在集群飞行器之间建立起来的通信连接模式,是高速飞行器组网设计的核心内容之一,合适的拓扑网络结构可以减少通信数据量,提高上层任务执行的效率和可靠性。在设计通信拓扑结构时,需要考虑飞行器之间的位置关系、飞行器的通信能力、飞行器的能量消耗情况以及对于上层任务的执行效率等因素[4]。

目前,飞行器集群常用的通信拓扑结构有星形拓扑、树形拓扑和网状拓扑等[5]。星形拓扑常用于集中式组网通信,即所有节点向一个中心节点连接,中心节点负责维护整个网络的通信,适用于节点数量较少的情况;树形拓扑常用于分层式组网通信,即节点之间按照一定的规则连接,形成一棵树状结构,适用于有中央协调单元的情况;网状拓扑常用于分布式组网通信,即节点之间任意连接,形成一个类似于网状的结构,适用于节点数量较多的情况。预先设计的通信拓扑网络的应用有一定的局限性,因此有学者对其加以改进。例如,文献[6]针对无人机集群中由于外界干扰引起的通信可靠性下降导致飞行器定位精度变低的问题设计了一种分层式协同通信算法来适应集群成员的异步更新。但是,在飞行器集群的动态环境下,通信拓扑结构可能会受到外界因素的影响,导致通信效率下降或通信中断,因此有许多学者对自适应通信拓扑网络进行了研究[7-8]。例如文献[9]受自然界中鸽群、椋鸟群的通信拓扑形式启发,设计了一种仿生自适应通信拓扑网络来消除集群控制抖振,提高编队的稳定性。文献[10]提出了一种自组织系统的群体控制方法,可以自适应固定和切换通信拓扑,实现智能单元的聚集和分散。

也有许多学者通过集群网络的拓扑重构来间接实现拓扑网络的环境自适应[11],主要的拓扑重构方法包括基于功率控制的拓扑重构方法[12],基于节点移动的拓扑重构方法[13],基于分簇的拓扑重构方法[14]。此外,人工智能技术可以作为一种有效的拓扑网络设计手段,例如,文献[15]提出了一种基于深度强化学习(Deep reinforcement learning,DRL)的通信网络拓扑设计方法,采用带有精英策略的学习算法能够实时生成低功耗、抗毁性强的自适应网络拓扑结构,但这些网络都是三连通的,通信量较大。

然而,目前研究中仍存在一些问题,例如对于如何在飞行器集群的高动态,多任务环境中实现快速有效的通信拓扑结构自适应,在降低网络通信量的同时提高集群鲁棒性的问题还鲜有研究。为了解决上述问题,本文提出了一种基于深度强化学习的自适应集群通信拓扑实时变构方法,通过与任务环境的不断交互可以学习到鲁棒的集群控制策略以及具备自主调整能力的集群通信策略,可通过改变集群个体与周围邻居的通信个数的方式自适应地调整通信拓扑网络。

1 问题定义

本节给出了高速飞行器的运动学模型以及定义了本文所研究的集群控制问题。

1.1 运动学模型

(1)

式中:V为高速飞行器的速度;γ为飞行路径角;ψ为航向角;RE为地心距;θ为地心经度;φ为地心纬度;g为重力加速度。

1.2 集群控制问题

集群控制的目标是建立一种集群控制器使得高速飞行器ui满足以下条件:

1)高速飞行器集群在飞行过程中尽可能保持初始队形;

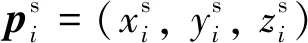
3)每个高速飞行器能够躲避环境中的威胁区。

因此,该问题可以表达为以下优化问题:

(2)

2 基于DRL的集群通信控制策略设计

在集群系统研究中,常假设任一个体可以获取集群内所有其他个体的状态信息,在对抗环境中,通信存在被干扰的可能,本文提出的基于DRL的集群控制策略通过观测空间、奖励函数和网络结构的设计,在保证集群编队队形保持、威胁区规避和目标打击能力的前提下优化通信策略,采用自适应的通信机制降低对通信的依赖。

2.1 基于强化学习的集群策略学习方法

如图1所示,基于柔性动作-评价(SAC)[16]的集群通信策略学习采用基于强化学习(RL)的数据驱动方法,在搭建的高速飞行器集群数值仿真环境中,与环境交互得到训练数据,利用数据不断优化集群控制策略。

图1 高速飞行器集群学习交互原理

设集群编队中每个飞行器的观测状态空间为S,输出动作为集群控制指令a∈A,A为动作空间。集群控制智能体从初始状态s0～p(s0)出发,根据策略分布at～π(·|st)采样输出一个控制指令at作用于集群环境,集群按输入的指令更新状态,得到一个奖励反馈r(st,at)并根据集群环境模型st+1～p(·|st,at)转移到一个新的状态st+1,一直循环此过程直到满足停止条件。一个循环过程称为回合(Episode)。定义一个回合的累积奖励

(3)

式中:γ∈[0, 1]是折扣率,γ→1使得学习到的策略更关注长期回报;T表示一个回合中智能体与环境交互的总步数。训练目标就是改进策略π,使得Gt最大化。

SAC是一种基于随机策略的RL框架,通过调整交叉熵来平衡学习过程中的探索和利用的关系,并且采用了双值函数网络、延迟更新和目标网络平滑等技巧,训练过程稳定波动小,是一种成熟的RL算法框架,因此本文选择其作为高速飞行器集群控制策略训练框架。算法流程包括以下步骤:

1) 初始化集群控制策略网络参数θ,集群控制策略值函数网络参数φ1和φ2及经验池D;

2) 设置值函数目标网络参数φtarg,1,φtarg,2分别与参数φ1,φ2相同:φtarg,1←φ1,φtarg,2←φ2;

3) 重复步骤4)～步骤14):

4) 观测集群仿真环境状态s,根据控制策略输出集群控制指令a～πθ(·|s);

5) 在集群仿真环境中执行控制指令a;

6) 观测下一状态s′和反馈的奖励r和回合结束标志位d;

7) 将经验组(s,a,r,s′,d)存到经验池D中;

8) 如果回合结束则重置环境状态;

9) 如果到达更新周期则执行步骤11～步骤14;

10) 从经验池D中随机采样一组经验B={(s,a,r,s′,d)};

11) 通过下式计算值函数的真值估计:

(4)

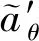
12) 通过梯度下降更新值函数网络:

(5)

13) 通过梯度上升更新集群控制策略:

(6)

14) 更新目标网络:

φtarg,i←ρφtarg,i+(1-ρ)φi,i=1,2

(7)

上述学习过程主要分为值函数学习和策略学习两部分:

(1)值函数学习

给定经验池D={(s,a,r,s′,d)},构造值函数网络Qφi的损失函数

(8)

式中:y(r,s′,d)为Qφi的值函数目标,即

(9)

式中:a′～πθ(·|s′)。SAC利用了Clipped Q-learning的技巧,计算值函数目标时取两个Q网络的最小值,避免对动作值函数的过估计。

(2)策略学习

策略学习根据值函数对高速飞行器集群给定飞行状态下输出的控制指令好坏评判,更新控制策略使未来的累计回报与交叉熵的和最大化,即

(10)

策略网络的输出a采用了重参数化(Reparameteri-zation)的技巧,即

(11)

式中:ξ～N(0,1)为标准高斯分布;μθ(s)和σθ(s)分别是策略网络输出的控制指令分布的均值和方差。基于SAC的集群编队、威胁规避和目标打击学习的是随机策略,输出控制指令按参数μθ(s)和σθ(s)采样后,再经过激活函数将控制指令输出限制到约束范围内。

在更新策略时采用同值函数更新一样的Clipped Q-Learning技巧,即

(12)

这样策略优化目标最终写成

(13)

可通过从经验池中采样的数据利用梯度上升法实现以上策略的优化。

2.2 观测空间

为了实现高速飞行器集群的编队、威胁区域的规避和对目标点的打击,需要在观测向量中包含这3部分信息,从而使集群控制策略能从观测中准确判别集群的当前飞行状况。

1)集群编队观测

① 相对队形信息

队形保持的目标是使得集群在飞行过程中高速飞行器之间的相对位置与初始时刻保持一致。设计观测信息为当前飞行器与邻近飞行器相对位置相比于初始相对位置的偏差量。首先对邻近飞行器i=1,2,…,m,计算当前相对位置

(14)

式中:RE为当前飞行器的地心距;θi,φi,hi为第i个飞行器当前时刻的经纬高;θ,φ,h为当前飞行器在当前时刻的经纬高。同理计算初始时刻飞行器i与当前飞行器的相对位置

(15)

式中:θi0,φi0,hi0和θ0,φ0,h0分别为第i个飞行器和当前飞行器在初始化时的经纬高。转换到当前飞行器当前时刻的速度系下

(16)

(17)

根据上述相对位置可得当前飞行器与邻近飞行器i的相对位置偏差

(18)

注意到式(16)中旋转矩阵均为当前时刻北天东坐标系到速度系的方向余弦矩阵,因此集群队形是在惯性系下定义的,若要队形在速度系下定义,将式(16)改为如下形式即可

(19)

(20)

式中:Rfmt为距离缩放因子,使观测向量中各维度处于同一量级。

②相对速度信息

相对运动信息的观测用于描述高速飞行器与集群整体运动趋势的一致性,因此选择个体与集群整体运动速度的偏差作为观测量。首先计算当前飞行器附近其他飞行器的平均运动速度

(21)

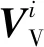
(22)

(23)

式中:Vi,γi,ψi分别为第i个飞行器的速度大小、飞行路径角和航向角,由于集群内飞行器间距相比地球半径很小,因此忽略飞行器i所在位置与当前飞行器所在位置北天东坐标系之间的转换。式(21)中wi为第i个飞行器速度所占权重,计算方式如下

(24)

(25)

(26)

从而相对速度的观测向量形式为

(27)

式中:Vfmt为速度缩放因子。

综上得到保持集群编队的观测向量如下所示

(28)

2)威胁区规避观测

(29)

(30)

转换到速度坐标系下

(31)

从而排斥向量为

(32)

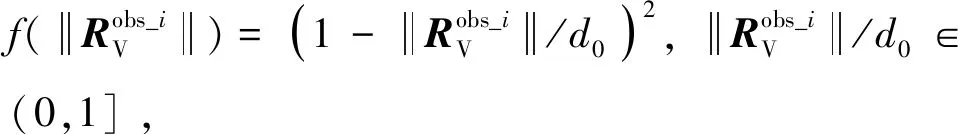
sost=eexc

(33)

3)目标打击

目标打击是高速飞行器集群的主要目标,即高速飞行器集群需最终命中目标点,在观测向量中需要包含与目标点的相对位置关系和相对运动关系。

首先计算目标与集群内任一飞行器的相对位置关系,根据目标点的经纬高[θtgt,φtgt,htgt],得到目标点相对于当前飞行器的位置矢量在当前飞行器所在位置北天东坐标下的分量

(34)

转换到速度系下

(35)

归一化为

(36)

(37)

综上,和目标打击相关的观测向量为

(38)

式中:Rtgt和Vtgt为缩放因子,使观测向量中各维度处于同一量级;stgt包含目标所在方位矢量,与目标相对距离信息,当前飞行器的飞行速度大小,以及当前飞行器当前运动状态下克服重力所需的过载。

综合上述观测向量,拼接得到总的观测向量为

s=[stgt,sost,sfmt]

(39)

2.3 动作空间

高速飞行器集群环境的动作a包含过载指令和通信指令,过载指令输入到1.1节的运动方程中完成集群相对运动状态的递推,通信指令用于确定与飞行器通信的最近的个体数量,调整集群通信拓扑结构,详细设计在2.5节网络结构设计中介绍。

2.4 奖励函数

奖励函数的设计与优化目标保持一致,基本原则为奖励好的状态和行为,惩罚与优化目标相反的状态和行为。与观测设计相对应,奖励函数设计也包含集群编队、威胁区域规避和目标打击3个来源。

1) 集群编队奖励

① 相对队形奖励

奖励函数是对智能体表现好坏的客观评价,因此在计算时可以获取集群内任意飞行器的状态而不受通信的限制。衡量集群相对队形的最直观信息是个体飞行器相对于“领机”的相对位置,在本文中以集群内所有飞行器位置加权计算一个虚拟的“领机”位置

(40)

式中:N为集群内飞行器总数。计算“领机”相对于当前飞行器位置矢量

(41)

同理初始时刻“领机”相对于当前飞行器位置矢量

(42)

式中:θld0,φld0,hld0为“领机”在初始化时的经纬高。从而相对于“领机”的位置的偏差表示为

(43)

此外在“领机”队形偏差基础上加入与邻近飞行器的队形偏差作为相对队形补充信息

(44)

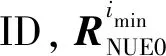
综上得到队形保持的奖励信息

(45)

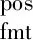
②相对速度奖励

集群内飞行器相对速度越小则运动速度一致性越高,因此设计飞行器个体与集群相对运动速度的奖励

(46)

2)威胁区规避奖励

威胁区规避的奖励函数设计为如下形式

rost=

(47)

3)目标打击奖励

目标打击的优劣准则是飞行器是否向目标点运动,因此通过飞行器的运动速度与目标方向的一致性来判断:

(48)

从而设计奖励函数

(49)

式中:ρ为一个正的系数。为了给智能体提供额外的提示,辅助训练收敛,在上述奖励的基础上添加位置奖励和距离变化奖励,当与目标距离在阈值Rtgt内时得到额外的奖励

(50)

式中:κ为一个正的奖励系数。

距离变化奖励是飞行器向目标点运动的奖励,通过计算每一仿真步长飞行器与目标点的距离变化得到

(51)

综上,总的奖励函数为

(52)

2.5 网络结构

根据前述算法原理,需要设计值函数网络和策略网络。值函数网络如图2所示,首先将集群编队信息、威胁区规避信息和目标打击信息拼接为观测向量,之后,观测向量和控制指令拼接后输入值函数网络,随后经过两层128节点的全连接网络,激活函数采用ReLU,最后经节点数为1的输出层得到值函数输出。

策略网络如图3,和值函数网络结构类似,首先输入层为拼接得到的观测向量,同样经过两层中间层,之后分4路,其中两路为2节点网络层,激活函数分别为Linear和Tanh,得到过载指令的均值和方差,另两路为单节点网络层,得到通信控制指令的均值和方差,两路信号分别按均值和方差经过高斯采样后经Tanh激活函数得到控制策略输出。

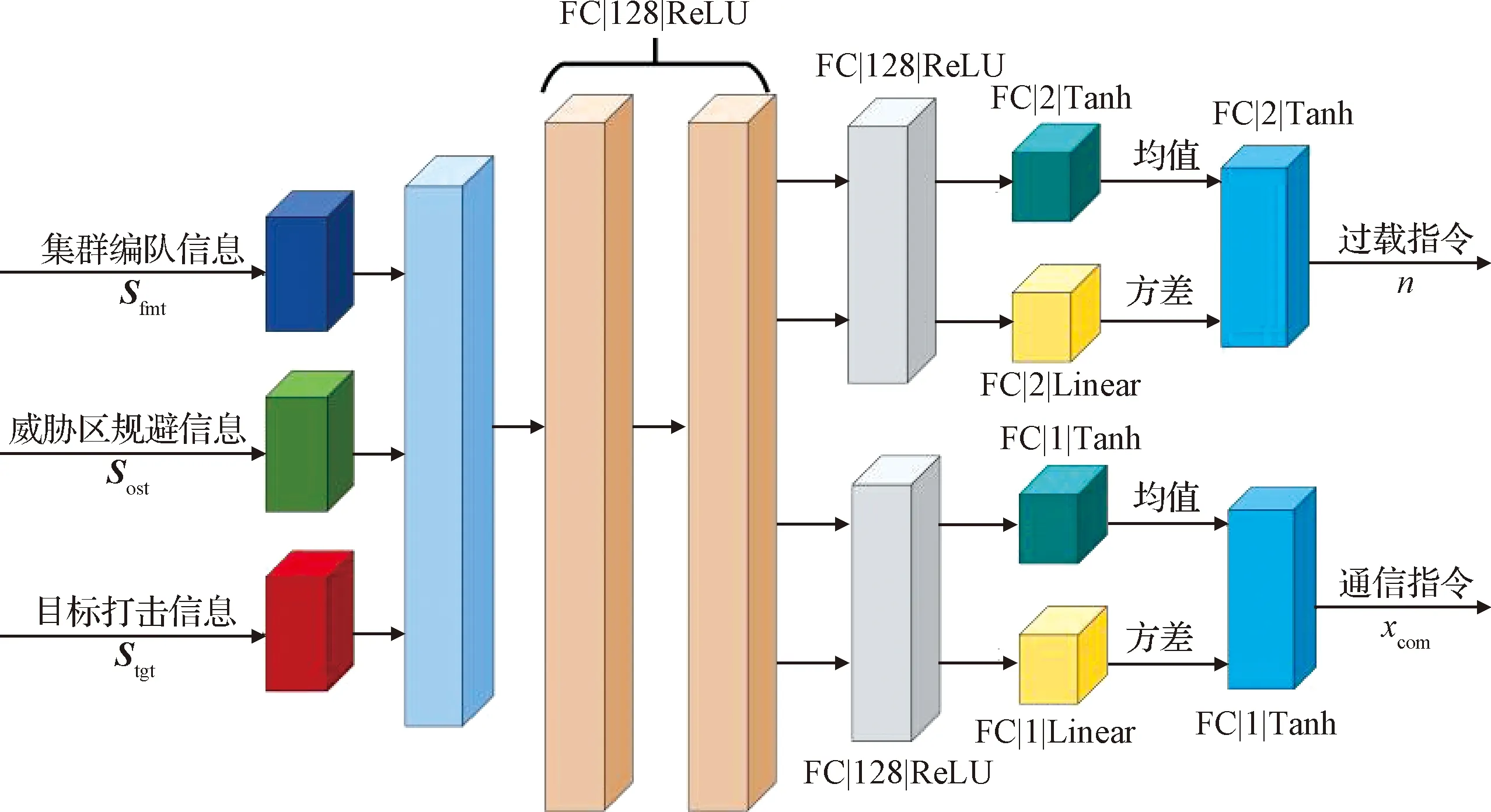
图3 策略神经网络架构

由于上述策略网络的输出是连续的实数域,而集群个体间通信数是整数,因此需要将网络输出作一定转换。由于策略网络在通信量的输出层激活函数为Tanh,取值范围(-1,1),设最大通信数量nmax,在每一个仿真步,设策略网络输出通信变量xcom,经过如下变换得到通信数量式中:策略网络的输出经nmax(xcom+1)/2取值范围变换为(0,nmax); ceil(·)为向上取整函数,将实数域转化为[1,2,…,nmax]的有限整数集合,从而得到通信的邻近飞行器数量。

(53)

3 仿真校验

3.1 仿真场景及算法参数设置

本文使用数值仿真的方法对所提的算法进行校验分析。其中,采用Python语言构建高速飞行器集群仿真环境。如图4所示,仿真环境中按照圆形形状均匀分布着9个大小相同的威胁区域,每个威胁区域以半径为10 km的半球形区域表示,且每个威胁区域中心距离分布圆形中心的距离为60 km。在每次训练开始时,将飞行器集群中的1号飞行器的初始位置设置在该圆形中心,其余飞行器按照设定的队形设置各自的初始位置。此外,在每次训练开始阶段,随机选择飞行器集群目标点的位置,其中随机设置飞行器集群中心与目标点的连线与坐标轴X轴的夹角,并且将飞行器集群初始位置到目标点的距离设置为130 km,以此产生随机且具有较高质量的训练场景。训练过程中使用10个飞行器组成的飞行器编队训练集群控制策略,每个飞行器的初始速度大小设置为1 km/s,初始高度设置为10 km。

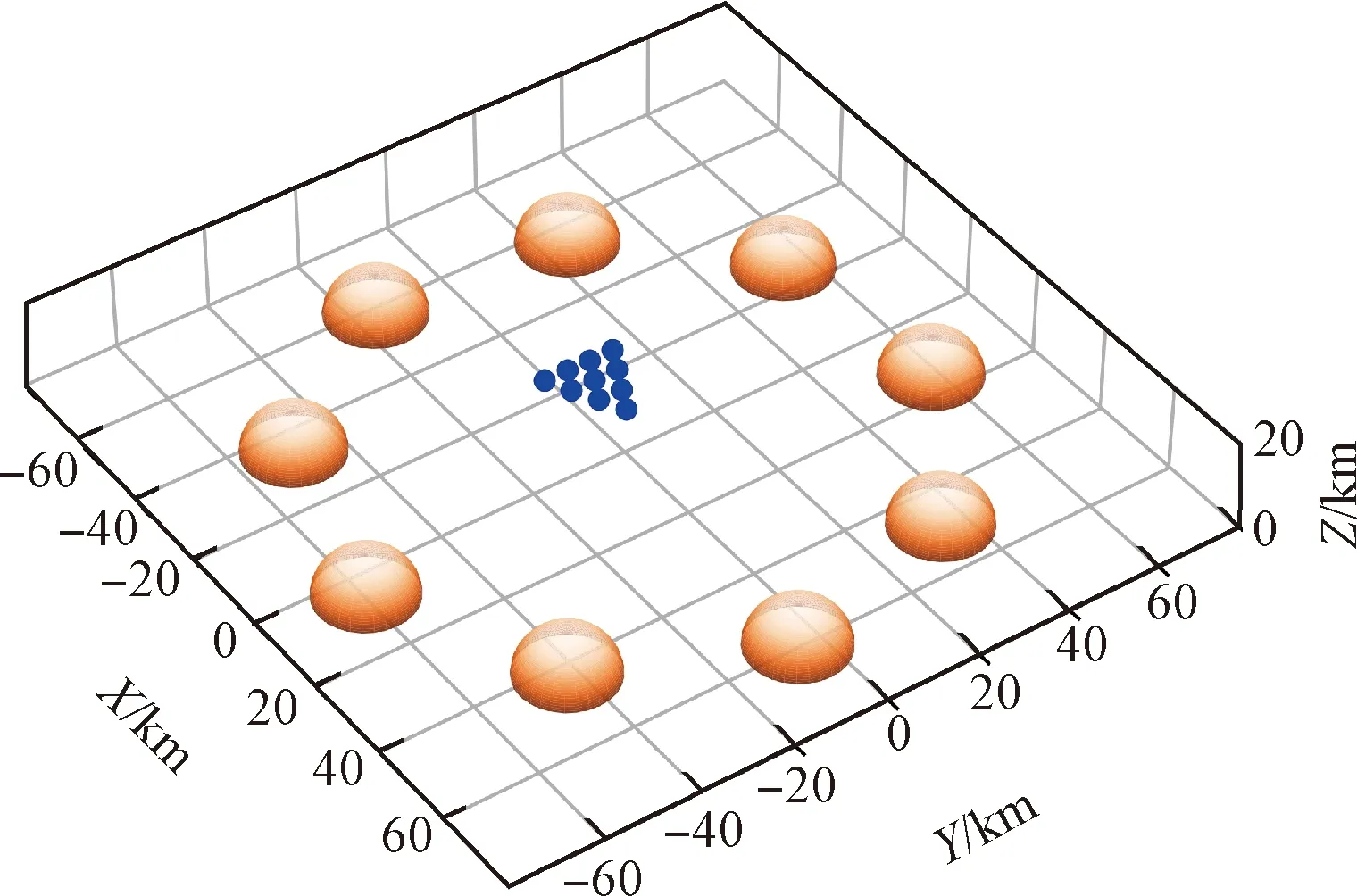
图4 仿真场景

其次,本文所提算法中的相关参数设置如表1所示,包括SAC算法参数、奖励系数、距离和速度缩放因子等。

表1 算法参数

3.2 训练结果

图5所示为不同通信机制下的集群控制策略在训练过程中所获得的奖励值曲线。图中所示曲线为每100个邻近训练周期中各集群控制策略所获得的奖励值平均值与方差,其中,曲线表示奖励值平均值,曲线对应的底色表示奖励值的方差。图中,在集中式通信机制下,1号飞行器为“领机”,其余飞行器为“从机”,所有“从机”飞行器只与“领机”飞行器通信,“从机”飞行器之间没有通信。在分层式通信机制下所有飞行器被自上而下分成多个层次,每一层指定一个“领机”飞行器,而这一层的所有飞行器都只接收该层“领机”飞行器的通信信息,其通信拓扑图如图6所示。在分布式通信机制下,所有飞行器与其周围的6个飞行器进行通信交互。在图5所示的4种通信机制下,集群控制策略的输入状态因通信机制的不同而不同,但是各集群控制策略的设计方式与第2节所述的设计方式一致。因此,影响各集群控制策略优劣的主要因素为各自的通信方式。

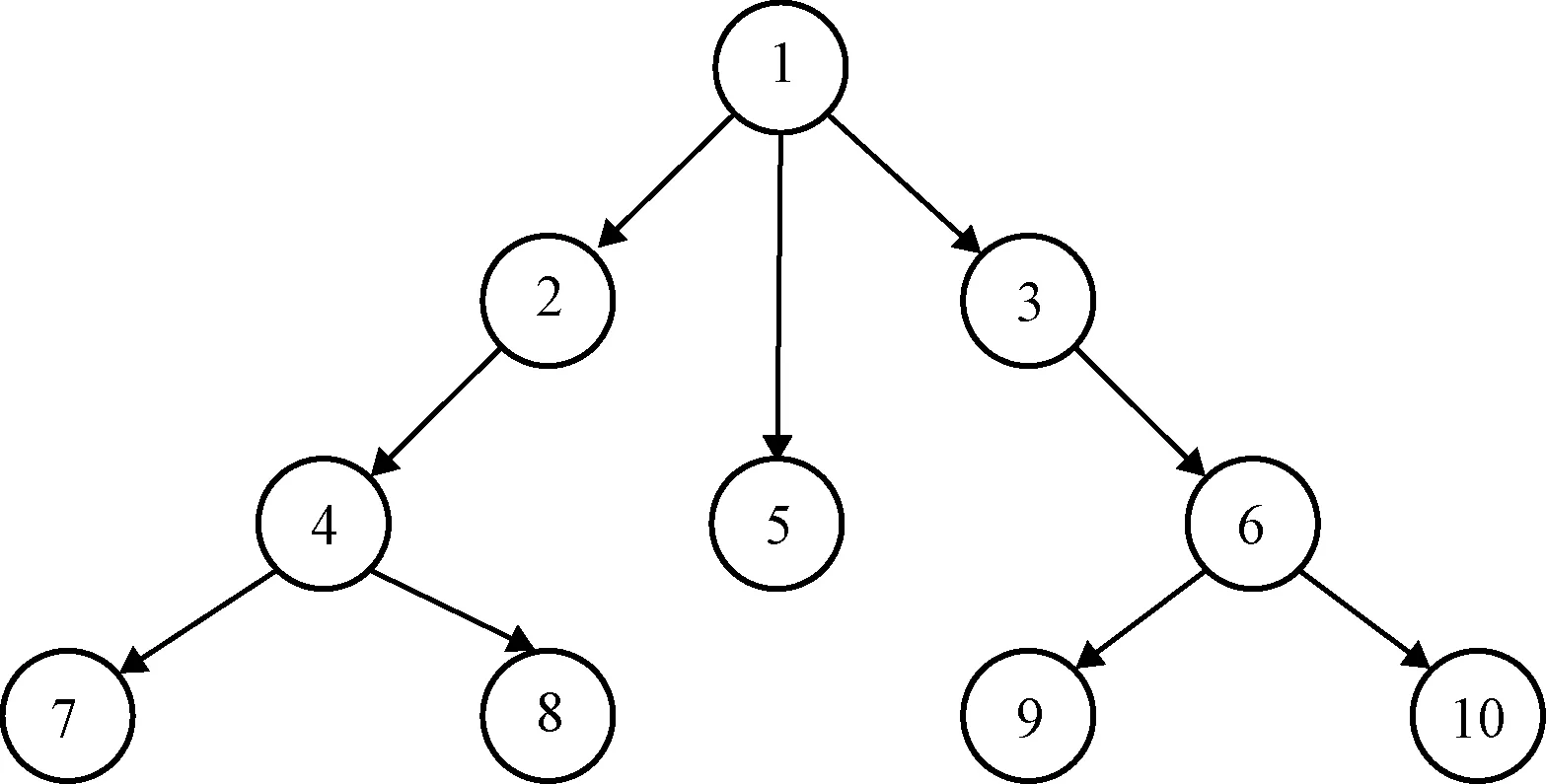
图6 分层式通信机制通信拓扑图

如图5所示,集群控制策略的训练共经历了2 000个训练周期,对于在以上4种通信机制下的集群控制策略,在训练了500次之后,其每回合接收到的累积奖励值基本保持稳定,表明集群控制策略的训练逐步收敛。在训练1 600次之后,可以看出自适应通信机制下的集群控制策略可以获得最高的奖励值,而集中式通信机制下的集群控制策略获得的奖励值最小,这部分地反映出自适应通信机制下的集群控制策略好于其他集群控制策略。为了全面准确地判断出以上4种通信机制下各集群控制策略的优劣,以下通过多种指标评价上述训练出的集群控制策略的性能。

3.3 对比结果

本文构建的集群控制策略的目标是控制高速飞行器集群在避免与威胁区发生碰撞的前提下尽可能地保持初始队形并且尽快到达目标点,并且在这一过程中自适应地调整通信拓扑,以适应较为复杂的集群飞行环境。因此,本文以队形保持精度Facc、目标点到达及时性Tg、威胁区避碰成功率Sta以及集群通信量Cf这4项指标评价各通信机制下集群控制策略的性能。

其中队形保持精度Facc定义为飞行器集群在由初始位置向目标点位置飞行过程中,其队形相对于初始队形的保持精度,即

(54)

目标点到达及时性Tg定义为飞行器集群由初始位置飞向目标点位置所用的时间T与设定的最大时长Tmax的比值,即

(55)

威胁区避碰成功率Sta定义为飞行器集群由初始位置飞向目标点位置的过程中,集群中的飞行器是否与环境中的威胁区发生碰撞,若没有发生碰撞,则Sta=1,反之Sta=0。

(56)

本文通过100次随机仿真实验计算以上4种指标在不同通信机制下的值,其中设置最大时长Tmax=200 s,最大通信数量nmax=6。计算的各指标数值如表2所示。

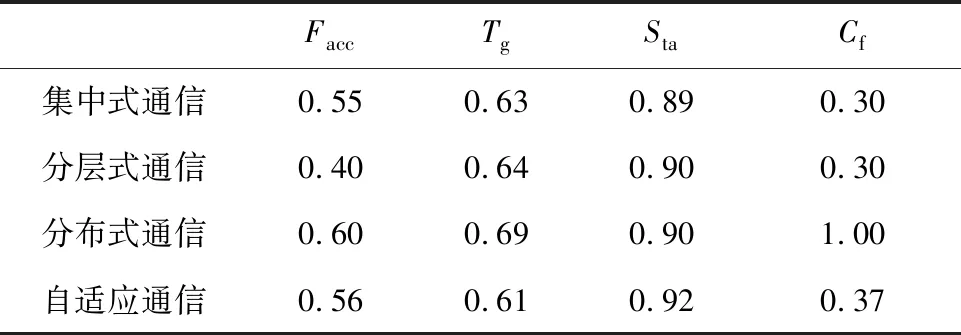
表2 不同通信机制下的评价指标数值

如表2所示,分布式通信机制具有最高的队形保持精度指标Facc,说明在本文所述的分布式通信机制下,对应的集群控制策略可以在飞行器集群飞行过程中较好地保持其初始队形。相对于分布式通信机制,自适应通信机制和集中式通信机制具有较差的队形保持能力,分层式通信机制具有最差的队形保持能力。这说明与周围个体通信的数量对队形保持能力具有一定的影响,从表2中的结果中可以看出,通信量越多,队形保持能力越强。相对于集中式通信机制,分层式通信机制的集群通信量虽然与之一样,但是由于分层式通信机制的分层控制机制,其队形控制能力弱于集中式通信机制。

对于目标点到达及时性指标Tg,自适应通信机制具有最低的指标值,表明其对应的集群控制策略可以控制飞行器集群快速地到达目标点,而分布式通信机制具有最高的指标值,说明其集群控制策略的及时性最差。影响分布式通信机制及时性指标的一个主要因素是保持较高的队形控制精度需要花费更长的时间。对于威胁区避碰成功率Sta,各通信机制下的指标值没有明显的区别,这主要是因为通信机制并不会影响飞行器集群对威胁区的观测状态。

对于集群通信量指标Cf,相比于分布式通信机制,自适应通信机制的集群通信量有了很大的降低,这说明本文提出的算法可以在保持队形控制精度与分布式通信机制相近的前提下尽可能地减小集群通信量。其次,虽然集中式通信机制与分层式通信机制具有最低的集群通信量,然而这两种通信机制中“领机”飞行器具有较大的通信压力,而且一旦“领机”飞行器出现故障,整个飞行器集群将无法继续完成任务,即集中式通信机制与分层式通信机制的鲁棒性远低于自适应通信机制的鲁棒性。因此,综合上述4项指标的对比分析可知,本文提出的自适应通信机制相对于其他3种通信机制具有更好的集群控制性能。

图7为以上4种不同通信机制下的飞行器集群飞行轨迹。由图可知,在所有4种通信机制下,当飞行器集群遇到威胁区时,其将自动调整队形,使得队形变得更加密集,以此规避遇到的威胁区。由图7(b)可知,相对于其他3种通信机制,在分层式通信机制下,飞行器集群在遇到威胁区之后其队形变的最为紧密,且在远离威胁区之后,飞行器集群没有恢复初始队形的趋势,因此其具有最低的队形保持精度。此外,由图7(d)可知,自适应通信机制下的集群控制策略可以在飞行器集群远离威胁区之后控制飞行器集群逐步恢复到初始队形,这说明其具有较好的队形保持能力。以上结果表明本文提出的自适应通信机制可以自主地调整飞行器集群的通信拓扑,在保证安全快速地完成既定任务的同时,尽可能地降低集群的通信量。

图7 不同通信机制下的飞行器集群飞行轨迹

4 结 论

针对高速飞行器集群的编队控制问题,本文基于深度强化学习框架提出了一种可自主调节通信数量的集群控制策略。其中,集群中的每个飞行器共享一个相同的控制策略,且集群控制策略的输出包含控制飞行器运动的过载指令以及其与邻居飞行器的通信数量。按照这种方式设计的集群控制策略更为灵活鲁棒,可在较低的集群通信量下安全快速地控制飞行器集群到达目标点并且较好地保持编队队形。数值仿真结果说明了本文所提算法的有效性。