配电网分布式电源和储能协调控制方法研究
2023-08-22车紫莹
车紫莹
(国网福建省电力有限公司 泉州供电公司,福建 泉州 362000)
0 引 言
能源的清洁高效利用离不开高水平的电气化,技术进步和成本下降必然会导致大规模的分布式电源并网,然而分布式电源由于其自身的特性,会对电网的稳定性造成影响[1-4]。针对这些问题,提出了一种新的基于分解的多目标优化算法,基于算法对多目标协调控制策略进行求解,最后在MATLAB 平台上验证了本研究的可行性和有效性[5-8]。
1 基于模糊理论的分布式电源出力
本研究中考虑的是风电模型,其模型表示为
式中:Pw,random为随机调度模型;Pw,fuzy为模糊调度模型。
Pw,random的大小主要受风速影响,风速密度均值函数可以表示为
式中:s为尺度系数;v为实际的风速大小;k为用来描述f(v)形状的值,一般在[1.8,2.8]内取值。Pw,random的具体表达式为
式中:vi、vo、vr为切入、切出与额定风速;Pr为额定输出功率。
在调度周期内,Pw,fuzy相对应的隶属度函数可以表示为
隶属度函数的形状由隶属度参数Pw1~Pw4决定,而参数Pw1~Pw4的取值公式为
式中:wk为比例系数,大小取决于风电出力的历史数据;Pfc为风电出力的预测值。梯形模糊参数可被表示为
2 储能充放电模型
充电过程为
放电过程为
式中:SOC(t)和SOC(t+Δt)分别为t、t+Δt时刻所储存的电量;Δt为时间间隔;ε为系统的剩余损失电量率;SOCchg(t+Δt)和SOCdis(t+Δt)为电池储能系统(Battery Energy Storage System,BESS)在t+Δt时刻的充放电功率,效率分别由α和β决定;SOCe为系统储能容量。
3 储能控制策略
本研究的储能设备选定为钠硫电池,并且考虑峰谷分时电价,储能控制策略的流程主要针对2种情况:(1)负荷大于分布式电源出力;(2)负荷小于分布式电源出力。当负荷大于分布式电源出力时,需要分布式电源和配电网同时提供电能;当负荷小于分布式电源出力时,仅需要分布式电源提供电能。
4 多目标协调控制策略
4.1 日成本
储能调度成本为
式中:KESS为系统单位调度成本;和为t时段内第m个系统的充放电功率。
风电发电成本为
弃风惩罚成本为
式中:Pwf(t)为系统被消纳的发电总量;ec(t)为风电上网电价。
微燃机发电成本为
式中:NG为总机组数;机组启停状态由h1,t确定;为l机组在t时刻的有功输出;同l机组的燃耗系数由a1、b1和c1共同确定。
微燃机启动停止成本为
式中:B1,t为当前l机组的启动停止成本。
4.2 日效益
电价效益为
式中:ed(t)、ew(t)分别为用户分时电价和风电补贴电价;Pe(t)、Pd(t)、Pw(t)分别为系统上网功率、用户负荷功率以及风机出力。
环境效益为
式中:m为风电总个数;n污染物的种类个数;HsCP、HsMG,j分别为火电机组第s项污染物排放总额和第j个风电第s项污染物的排放总额;Ve,s为第s项污染物减排价值。
节能效益为
式中:Mc为共消耗煤炭总额;pc为单价;Pw,j为第j个系统发电总量。
4.3 目标函数
本研究基于模糊理论提出了一种新的多目标协调控制策略,控制目标如下:目标函数定义为日净利润PPRO的最大化函数,综合前面的日成本和日收益,PPRO最大值为
5 多目标协同控制策略求解算法
MOEA/D 算法的流程如图1 所示。为了克服最优前沿形状的不确定性,本研究基于切比雪夫分解法分解多目标优化问题[9,10],其数学表达式为
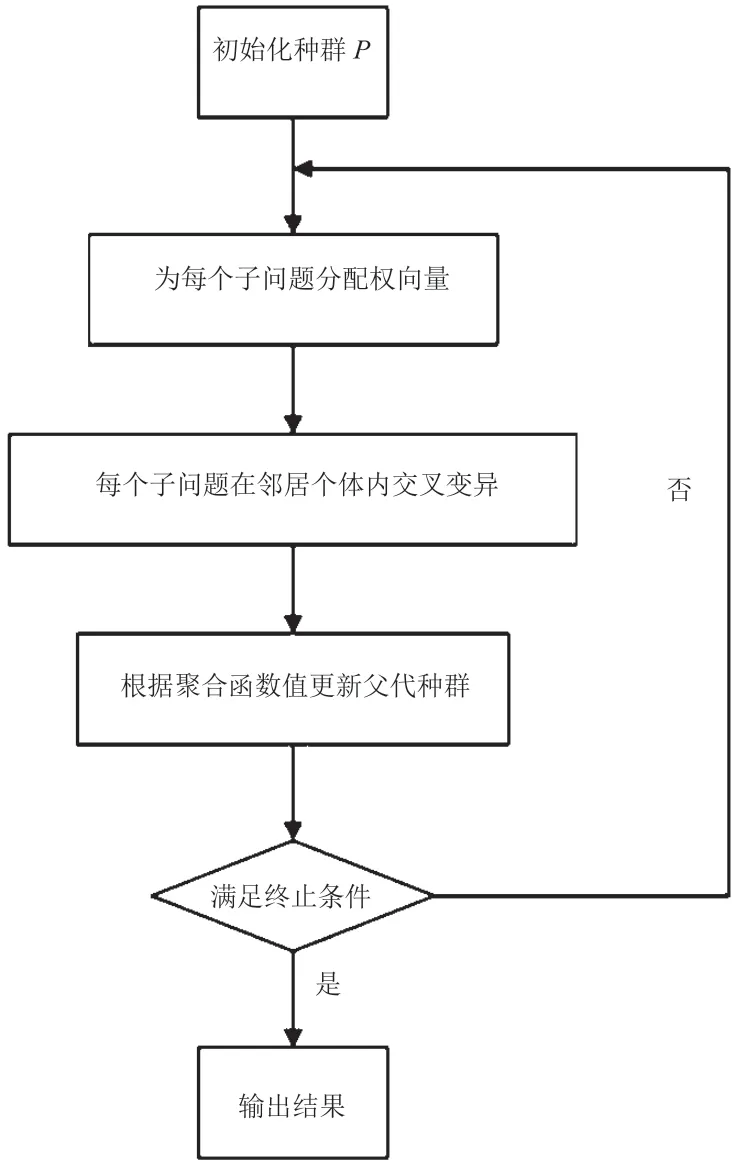
图1 MOEA/D 算法的基本流程
式中:m为目标函数数目;z*={z1*,…,zm*}T为参考点;λ={λ1,…,λm}为权重向量。
6 仿真验证
文章选择改进后的IEEE33 节点电力系统作为研究对象,如图2 所示。
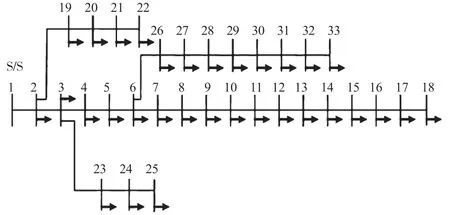
图2 IEEE33 节点配单网系统
仿真后得到的并网前后负荷需求对比如图3所示,可以清晰地看到,并网后负荷的需求、波动、峰谷差相较并网前都有明显降低,并且有良好的削峰效果。另外,储能并网改变了负荷峰值出现的时间,降低了配电网的备用容量。以上手段能够降低负荷的波动性,提高经济效益。
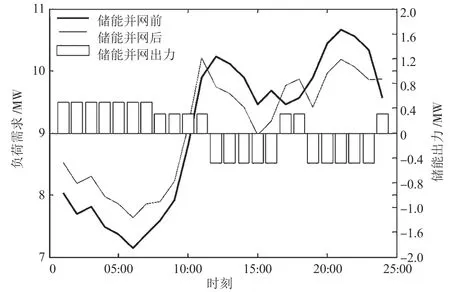
图3 储能并网前后的负荷需求
7 结 论
本研究的研究对象为风力分布式电源,将电源处理作为模糊变量并建立了相应的可信性分布函数及隶属度函数;提出系统充放电模型并制订了相应的储能控制策略。另外,基于所给出的IEEE33 节点电力系统,在MATLAB 平台上进行策略有效性验证。
