Hopfield神经网络的同步性控制

李 蕾

(淮北师范大学 数学科学学院, 安徽 淮北 235000)

Hopfield神经网络在过去的二十年中,由于在建模复杂动力学方面的潜在应用,已经成为一个活跃的研究领域,成功地应用于解决各种线性和非线性规划问题,引起了人们的广泛关注[1-6].近年来,由于实际系统中存在不确定性,随机系统的同步性一直是研究的热点问题,随机建模在科学和工业的许多分支中起着重要的作用.一个真实的系统通常受到外部扰动的影响,而外部扰动在许多情况下具有很大的不确定性,因此可以被视为随机的.因此,考虑随机效应对Hopfield神经网络稳定性的影响是非常重要的.

由于现实世界的网络通常有大量的节点,通过在所有节点上添加控制器来控制复杂网络通常是困难的.为了减少控制器的数量,一种自然的方法是通过牵引住部分节点来控制网络.事实上,许多实际系统经常突然受到外部干扰,使系统在很短的时间内改变轨迹.因此,具有脉冲效应的动态网络的研究对于理解最真实世界的网络的动态行为具有重要意义.[7]Liu采用牵引控制技术,研究了非线性耦合网络的固定同步问题,包括递归连接神经网络、细胞神经网络、Hodgkin-Huxley模型、Lorenz混沌振荡器等.[8]Liu利用反应-扩散耦合:空间耦合设计了一种新的分布式耦合协议,研究了具有时变时滞和反应-扩散项的线性耦合神经网络的非周期性间歇牵引控制的完全同步问题.[9]Sanchez利用递归高阶神经网络进行辨识,提出了一种对未知耦合强度变化的复杂网络进行牵引控制的新方案,以实现同步.

由于其具有适当自适应律的自动调节功能,能够保证更好的性能和提供用户期望的结果,自适应控制器已成为研究人员中最好的实时控制器之一.[10]Chen通过一种周期性间歇牵引自适应控制策略,利用时滞积分不等式方法来克服随机扰动、中立项和时变时滞共存所引起的障碍,研究了具有时变时滞的中性随机耦合神经网络.[11]Zhou针对非线性多节点神经网络参数未知的问题,提出了响应系统权值的更新规律和自适应控制器的增益,实现了延迟多节点神经网络的同步.[12]Wang基于Lyapunov方法和Kirchhoff矩阵树定理以及微分不等式技术,对所考虑的模型推导出新的同步条件.[13]Li利用自适应控制技术,构造了一个新的Lyapunov泛函,设计了自适应更新律,导出了具有时变时滞的忆阻神经网络的两个同步准则.

在上述讨论的基础上,本文创新点如下:

1)设计合适的自适应控制器以及构造合适的Lyapunov-Krasovskii泛函(LKF),保证Hopfield神经网络主-从系统的同步,给出了Hopfield神经网络的自适应控制同步性的充分条件.

2)设计合适的牵引脉冲控制器以及结合李雅普诺夫稳定性理论、LaSalle不变准则和一些分析技术,得到了Hopfield神经网络的牵引控制同步性的充分条件.

1 预备知识

考虑如下形式的Hopfield神经网络:

(1)

其中:i=1,2,…,n;ai为连接权重;Tij表示第i个神经元与第j个神经元之间的强度;f(x(t))=(f(x1(t)),f(x2(t)),…,f(xn(t)))为神经元的激活函数.

相较于主系统(1),设计如下形式的从系统:

(2)

其中:ui(t)为待设计控制器,令x(t)=(x1(t),x2(t),xn(t))T,y(t)=(y1(t),y2(t),yn(t))T,ei(t)=yi(t)-xi(t),则误差系统的动态方程为:

de(t)=[-Ae(t)+T⊗F(e(t-τ(t)))+u(t)]dt

定义1 系统的主-从系统实现同步,若满足

假设1 存在正常数Fi,使得对一切s∈R有

|fi(s1)-fi(s2)|≤Fi|s1-s2|

为了实现Hopfield神经网络的自适应同步性,设计如下形式的控制器:

u(t)=k(In⊗F)e(t)

当考虑系统的牵引控制同步性问题时,考虑形式如下的误差系统动态方程:

为了网络全局指数稳定,设计如下形式的牵引脉冲控制器,控制的节点数l≪n:

LV(x,y,t)≤β(t)-w1(x)+w2(x),(x,y,t)

∈Rn×Rn×R+,

w1(x)E>w2(x),∀x≠0,

引理2[16]对于任意的p,xi,yi,δi>0,有

引理3[15]令X,Y为任意的n维实向量,为正定矩阵,以及P∈Rn×n,则有以下矩阵不等式成立:

2XTPY≤XTR-1PTX+YTRY

若x,y为实向量,则存在Q,使得

成立.

破解派遣员工管理困局 着力提升窗口服务质量（凌彩虹） ............................................................................3-24

2 同步性判断依据

定理1 在上述假设和引理2成立条件下,Hopfield神经网络的主-从系统可以实现自适应同步性,若有不等式

-2AP+δTFP-2Pκ<0

证明：

则

由LaSalle不变准则可知,在上述控制器下的主-从误差系统可达到同步状态.

[r2(n-1)g1+g2f]<0

恒成立,其中:

g1=max{|Tij|,j≠i},g2=max{|Tii|},r1=λmin(R),r2=λmax(R),f=max{|Fi|},a=min{ai}.

证明：

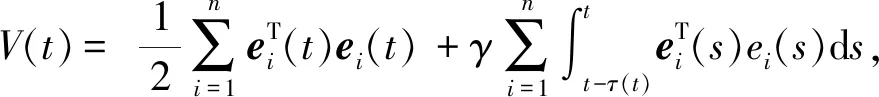
综上所述,可得

当t=tk时,

可得∀t≥t0,V(t)≤V(t0).定义V(t)如下形式的水平集

3 数值例子

考虑如下形式的Hopfield误差神经网络

de(t)=[-Ae(t)+Tg(e(t-τ(t)))]dt

当n=2,主-从系统矩阵定义为

从而可以得到

-2AP+δTFP-2Pκ<0

符合定理条件,所以由定理3.1可知,Hopfield神经网络的主-从系统可以实现同步性.

图1 主-从系统同步状态

根据主-从系统同步状态图可知,误差系统可达到同步状态.

4 结 语

本文通过设计合适的自适应控制器以及牵引脉冲控制器来处理Hopfield型神经网络的全局同步问题,利用李雅普诺夫稳定性理论、LaSalle不变准则和一些分析技术得出了系统同步的充分条件,与现有方案相比,它更适用于许多重要的实际领域,如自动控制系统的分析和人工神经网络的设计,因此具有广泛的应用前景.