瞬态流体激励下离心泵转子振动特性研究

任映霖 李 帅 王 威 李启行

（北京化工大学 高端机械装备健康监控与自愈化北京市重点实验室）

离心泵是一种以叶轮为核心部件的旋转式流体机械，是石油化工、航空航天及船舶等领域的重要组成设备。离心泵运行时产生振动的原因有多种，其中不平衡质量和流体激励是引起泵转子与壳体振动的主要因素。

在离心泵运行过程中，其非定常流动时刻存在，其中在叶轮与蜗壳之间的动静交界面处压力波动比较剧烈，易出现干涉现象，影响了内部压力脉动瞬态特性［1］，进而引发泵体的结构振动［2］。叶轮和导叶的匹配特性往往对压力脉动起主导作用，针对不同导叶型式的离心泵，在变流量和变转速实验中，可以验证离心泵内的压力脉动、作用在叶轮上的流体激振力、蜗壳内的压力值与泵轴的振动位移之间的相关性［3］。实验和仿真表明流体激振力主要来自叶轮表面的径向力。针对径向力产生的原因，黄思和吴玉林对单级蜗壳式离心泵全三维流场进行了数值计算，发现叶轮各通道的流量、流速及压力分布等表现出明显的非对称性，由于非对称的存在导致了较大的径向力［4］。JIANG W等对带导叶离心泵进行数值模拟和实验研究，得到作用在离心泵叶轮上呈周期性变化的流体激振力，结果表明，导叶越靠近蜗壳隔舌，叶轮上流体激振力越大［5］。在对激振力进行简化时，BARRIO R等通过仿真及实验验证了离心泵在非设计工况运行时，作用在叶轮上的流体激振力非定常分量约占平均量的40%～70%［6］。

而较大的激振力会导致泵转子及其蜗壳的振动，在流场非定常计算过程中，对于低比转速泵，一般将叶轮所受时域脉动压力通过FFT转换到频谱并以之作为泵组结构的振动激励源，采用隐式有限元方法进行泵组结构振动响应的计算［7］。高速泵在运行过程中，不平衡质量与流体激励是导致转子系统振动过大及其轴心轨迹紊乱的主要原因，并且在脉动激振力作用下，泵转子振动响应谱图中出现了脉动激振力的频率及其谐波频率［8］。叶轮上流体激振力通常以集中力与集中力矩的形式加载到转子上，该方法能够同时有效计算出离心泵运转过程中转子的响应和流体激励所诱发的基座振动值［9］。同时单级泵转子的不同位置在流体激振力与不平衡质量作用下表现出不同的特性，在不考虑转子上不平衡质量时，叶轮位置横向振动幅值最大，在考虑转子上不平衡质量影响时，转轴中部横向振动幅值最大［10］。对于多级泵，可以结合CFX与SAMCEF转子动力学分析软件，计算不同工况下高速井泵的转子的临界转速和振型，并对该转子系统进行瞬态分析，得到泵转子各级叶轮位置的响应曲线［11］。刘栋等利用COMSOL软件对比了单、双蜗壳模型泵转子的振动特性，计算了双蜗壳模型泵转子的振动位移、轴心轨迹［12］。

目前，与泵转子瞬态动力学分析相关的研究，通常只考虑了额定工况或单一工况。笔者以离心泵非定常CFD数值模型和泵转子有限元动力学模型为研究对象，将流体激励以时变载荷的形式施加在泵转子动力学模型上，采用Newmark-β隐式算法计算瞬态响应。研究离心泵转子在不同工况下不平衡质量力与非稳态流体激振力共同作用下的振动特性，同时对比不同工况下转子不同位置的动力学响应，得出不同工况下不同方向的响应规律，相关研究将有助于分析泵转子运行稳定性。

1 数值模拟

1.1 流场计算模型

以一台IS型单级单吸离心泵为研究对象，模型以CFturbo软件进行设计，UG软件进行装配，如图1所示。采用FLUENT软件基于有限体积法进行非定常计算。计算域包括进口段、叶轮、蜗壳和出口段。对比了ANSYS Mesh和FLUENT Meshing网格划分，FLUENT Meshing划分出的网格数量少，并且网格的整体质量更高，故采用FLUENT Meshing模块进行网格划分。由于叶轮流道较复杂，采用多面体核心网格进行划分，边界层取5层，数值计算网格数量具体为进口段20 896、叶轮589 443、蜗壳及出口段290 707，共计901 046个网格。

图1 流体域装配

1.2 控制方程及湍流模型

针对湍流问题，在CFD中有不同湍流模型，其中应用较多的是基于雷诺时均方程的统计模型，并联立相关的脉动耗散率及湍动能方程，形成完备的模型方程组。在进行泵内部流场的CFD分析中，多数采用RNG k-ε湍流模型和SST k-ω湍流模型［13］。在近壁区，SST k-ω湍流模型要比RNG k-ε湍流模型更加准确。非定常计算以定常计算为初始值，同时对初始值较为敏感，因此在稳态计算时，先后对比了RNG k-ε湍流模型和SST k-ω湍流模型算法，在额定工况下，利用SST k-ω湍流模型监测得出的扬程与理想扬程误差小于5%，故文中选择SST k-ω湍流模型。

1.3 边界条件及求解

离心泵进口边界按设计点质量流量设置，出口边界为压力设置，采用无滑移固壁条件，并使用标准壁面函数确定固壁附近流动。叶轮旋转速度为1 450 r/min，其中叶轮流体域与蜗壳流体域以interface界面连接。

叶片转角在2～3°时离心泵瞬态流场较稳定，以2°为一个时间步，取非定常数值模拟时间步长为2.3×10-4s。根据文献［14］可知，叶轮在旋转6～8圈之后达到稳定，故本次设置叶轮旋转周数为12圈。计算中对各控制方程进行二阶中心差分，收敛标准为各参数平均残差值小于1×10-5，同时以监测进出口压力、扬程作为收敛依据。不同工况下的边界条件见表1。

表1 不同工况下的边界条件

1.4 非稳态流体激振力

离心泵转子在流体作用下产生振动位移的直接原因是作用在叶轮上的径向流体激振力。这种流体激振力是由作用在叶轮各叶片和前后盖板表面上的流体压力和流体粘性力合成，在CFD软件后处理中对以上分散的力在叶轮表面进行积分［15］：

叶轮所受径向力向量为叶轮旋转位置或时间的函数，如：

基于仿真所得非定常流场，得到叶轮空间上3个坐标轴方向随时间变化的流体激振力，其中叶轮各表面沿旋转轴x轴积分得到轴向力Fx，沿y和z两个方向积分得到互相垂直的径向力Fy和Fz。通过改变离心泵进口的流量，获得5种不同流量下叶轮所受到的径向力激振力。尽管离心泵在设计工况下的理想径向力合力要求为0，但在实际运行过程中，径向力不会完全消失。以不同工况下的径向力作为流体激振力，图2、3分别为不同流量下非稳态流体激振力的时域分析和频域分析。由于离心泵隔舌和蜗壳的存在，导致泵结构不对称，两个方向的径向力大小存在一定差异，整体上y方向的径向力大于z方向的。叶轮的转速为1 450 r/min，故转频F=24.17 Hz，叶片数Z=6，则一倍叶频T=145.02 Hz，不同工况下的叶轮径向力在一个周期内均呈现6个峰值，峰值数与叶片数保持一致且具有周期性。从频域图中可以得到，流体激振力由多个频率成分组成，其中主要成分为一倍叶频（145 Hz）、二倍叶频（290 Hz）、三倍叶频（435 Hz）等，随着偏离设计工况点，激振力逐渐增大。

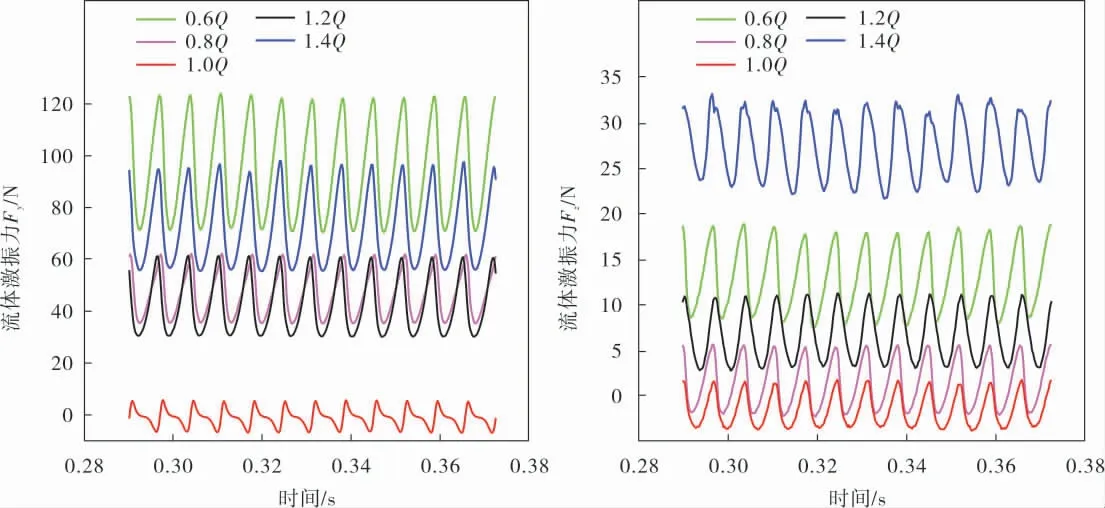
图2 不同工况下瞬态流体激振力时域

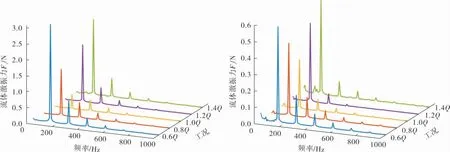
图3 不同工况下瞬态流体激振力频域

2 泵转子分析

2.1 转子有限元模型

离心泵转子三维模型如图4所示，二维有限元模型如图5所示，与在ANSYS软件中进行实体建模相比，此方法更简洁且计算时间大幅度减小，对此类旋转机械转子动力学特性有较好的模拟效果。

图4 泵转子三维模型

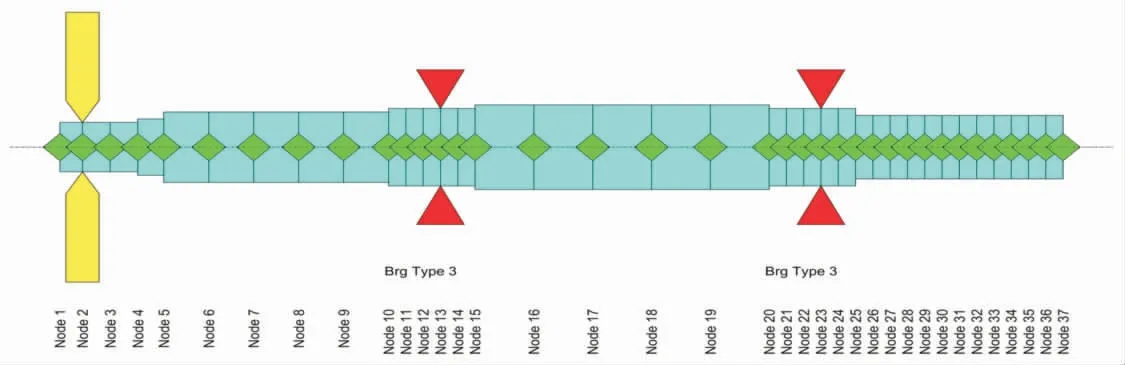
图5 泵转子二维模型

泵轴材料为40Cr，弹性模量为200 GPa，泊松比为0.27，密度为7 870 kg/m3，质量为8.697 kg，直径转动惯量为0.073 75 kg·m2，极转动惯量为0.04 kg·m2。泵转子为卧式结构，共36个单元，37个节点，其中叶轮位于节点2处，节点13与节点23处为滚动轴承。

2.2 不平衡质量与流体激振力作用下转子瞬态响应分析

取叶轮在旋转第8～11圈中的周期激振力，通过激振力延拓的方式对转子模型重复加载。同时，转子不平衡质量施加在两个轴承的中间节点（17号节点）处。采用Matlab编译的Newmark-β隐式算法对存在不平衡质量与非稳态流体激振力的转子进行瞬态响应求解。

当转子系统在激励载荷作用下运行时，将不平衡激振力与流体激振力的合力记为Ft，载荷Ft是与时间t相关的函数，在t时刻转子系统运动微分方程表示为：

该方法通过逐步积分求解，具有较好的稳定性。Newmark-β法基本假设表示为：

将式（6）改写为：

将式（7）代入式（5）得：

t+Δt时刻动力学方程表示为：

将式（7）、（8）代入式（9）得：

其中：

图6为不同工况下泵转子叶轮的位移响应。叶轮处振动主要受叶轮流体激振力影响，叶轮振动规律与径向力的分布规律相关，在一个周期内呈现出6个峰值，同样与叶轮叶片数相对应。

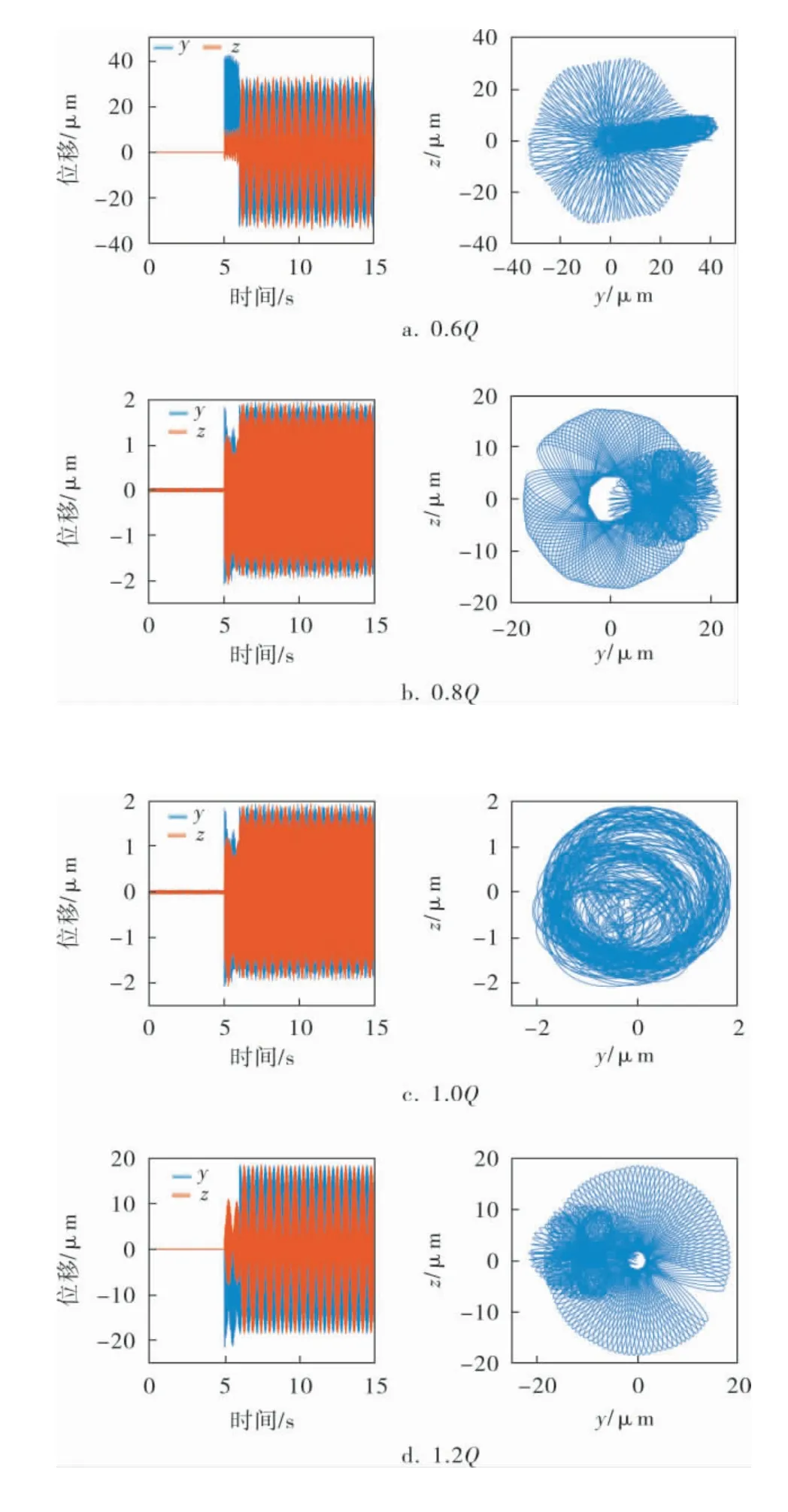
图6 不同工况叶轮处位移响应及轴心轨迹

由图6可见，0～5 s为泵转子在只有不平衡质量作用下的响应。流体激振力在第5 s开始加载到转子上，有流体激振力作用时，位移响应迅速增大。工况从0.6Q到1.4Q变化时，叶轮处振动位移差别明显。设计工况下两个径向位移幅值较接近，由表2可见，y向的振动峰峰值为0.004 0 mm，z向振动峰峰值为0.004 1 mm，与泵转子理想状态接近。0.6Q工况下叶轮所受y向径向力最大，故在该工况下的位移响应最大，最大值为0.042 7 mm，振动峰峰值为0.076 0 mm。由于径向力的作用，不同工况下y方向的振动峰峰值均大于z方向的，随着偏离设计点，径向振动位移增大，峰峰值也逐渐增大。

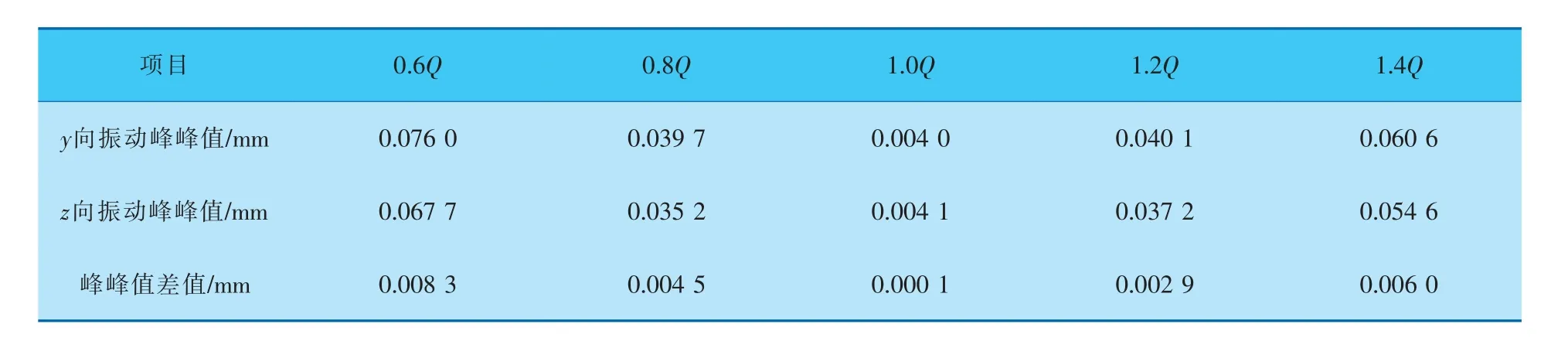
表2 不同工况下叶轮振动峰峰值

在泵转子无流体激励力的情况下，只存在不平衡质量，转子的轴心轨迹较规律，而在有流体激励力的情况下，转子轴心轨迹较混乱，轴心轨迹规律性不明显。对比其他工况，由于0.6Q工况下叶轮承受的径向力较大且分布不规则，导致轴承处的偏心明显，出现转子-轴承系统运行不稳定的现象。轴心轨迹在设计工况下最稳定，偏离设计工况越多，轴心轨迹越不稳定。当工况从1.0Q到0.6Q变化时，轴心向右偏移，而工况从1.0Q到1.4Q变化时，轴心轨迹逐渐向左偏移。

不同工况下，转子系统在轴承处的位移响应如图7所示。

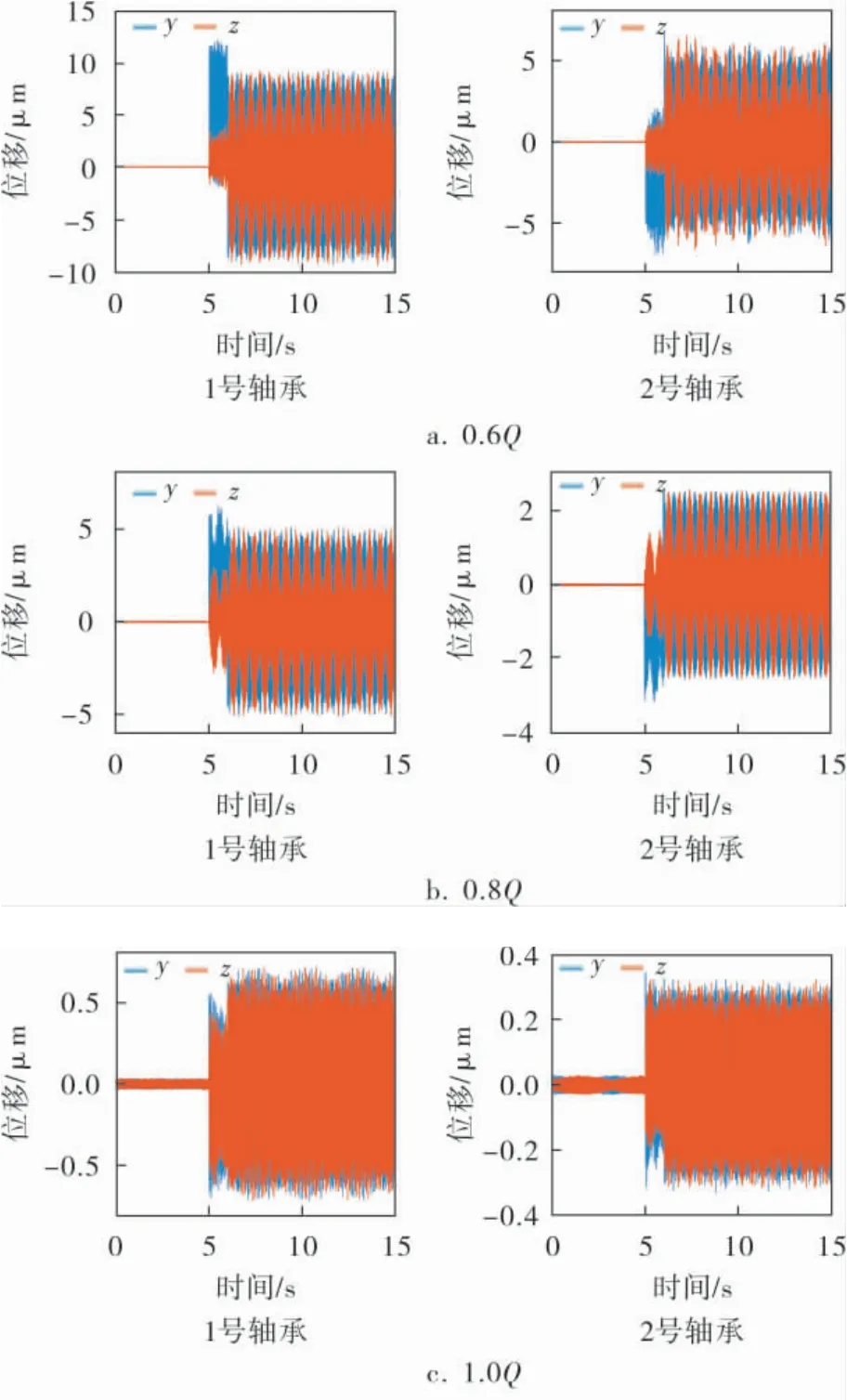
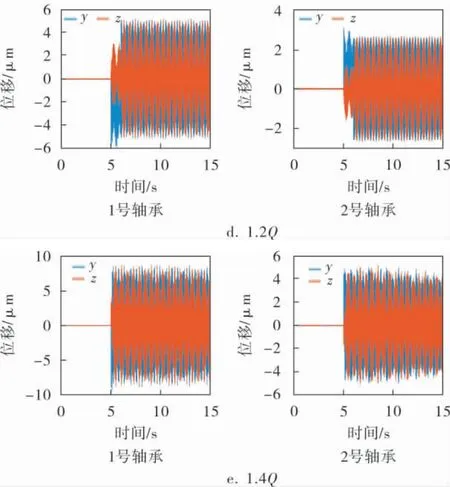
图7 轴承处位移响应

由 表3、4可 见，1 号 轴 承 与2 号 轴 承 都 是 在0.6Q工况下振动位移值最大。1号轴承y与z两个方向振动峰峰值分别为0.021 6、0.018 8 mm；2号轴承在y与z两个方向振动峰峰值分别为0.013 6、0.013 1 mm。对比1号和2号轴承y和z两个方向振动峰峰值可知，1号轴承的峰峰值明显大于2号轴承的峰峰值，其原因是2号轴承远离叶轮，受流体激振力影响较小。设计工况下1号轴承与2号轴承振动幅值较为接近。随着偏离设计工况，轴承处振动峰峰值增加，由此可见，振动峰峰值的大小与流体激振力密切相关。

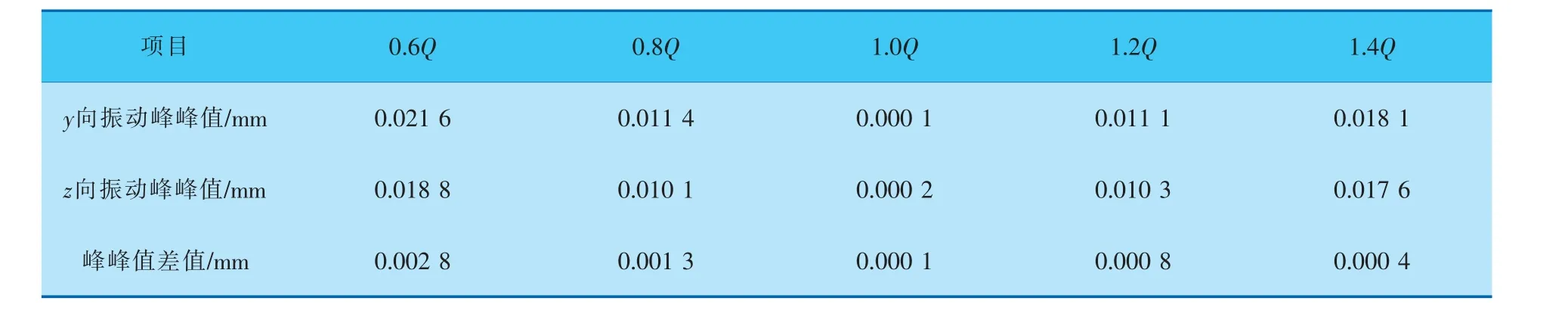
表3 不同工况下1号轴承振动峰峰值

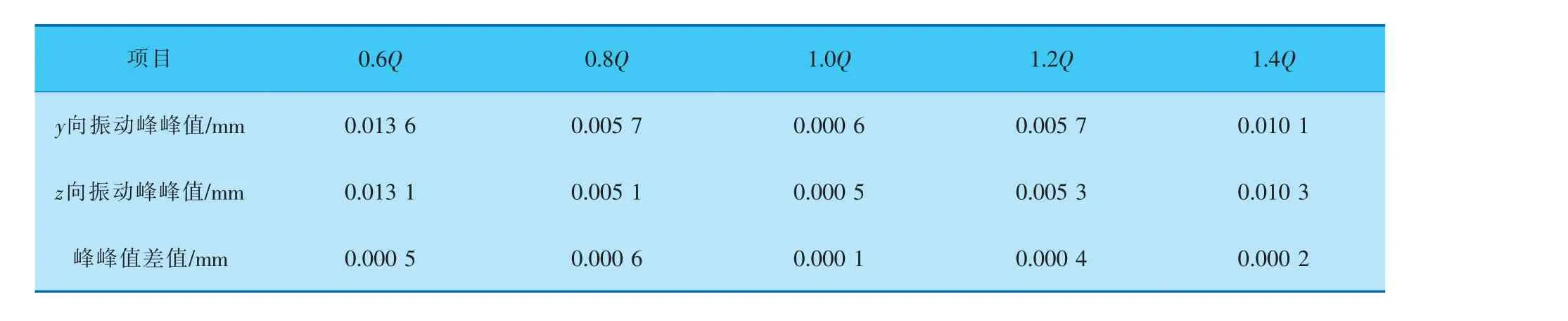
表4 不同工况下2号轴承振动峰峰值

对比表2与表3、4可以看出，叶轮处转子在不平衡力与非稳态流体激振力作用下的振动幅值最大，其次为轴承处。

3 结论

3.1 对泵叶轮所受到的力进行快速傅里叶变换，发现其所受到的流体激振力主要为一倍叶频、二倍叶频及其倍频。

3.2 泵转子的峰峰值和振动位移的最大值均随着运行工况偏离设计工况点的增加而增大。

3.3 当泵的运行工况偏离设计工况时，小流量工况（0.6Q）相较于大流量工况（1.4Q），泵转子的振动幅值更大。

3.4 当考虑转轴中部存在不平衡质量时，叶轮处在流体激振力作用下的振动幅值最大，其次为1号轴承、2号轴承。