高速铁路动检车检测数据里程偏差修正算法研究

张宝美，岑敏仪，张同刚，黄 亿，江来伟

(1.西南交通大学地球科学与环境工程学院,成都 610031; 2.广深铁路股份有限公司广州南高铁工务段,广州 511495)

引言

拥有高精度里程信息的轨道检测数据,是评估轨道几何状态的关键基础[1]。动检车由于受到轮轨之间的相对蠕滑、车轮磨损、GPS信号不稳定等因素影响,导致其所检测的里程信息往往和实际线路里程信息不符[2-3]。这种不符的存在不仅影响轨道病害位置的准确定位,延误轨道病害区段的维修工作,还使得动检车在不同时期检测的轨道不平顺数据存在里程偏移,不具备可对比性,直接影响轨道不平顺状态评定、预测结果和养护维修计划的有效性。

对于轨道不平顺数据存在里程偏差,国内外学者提出许多减少里程偏差的方法,主要分为两大类:提高传感器硬件精度和用数学算法修正里程误差。如在动检车上安置全球定位系统GPS[4]和差分定位系统DGPS[5]在线实时自动修正里程偏差,该技术已广泛用于我国GJ-4、GJ-5、GJ-6等类型动检车[4]。刘小磊和郭迎分别提出采用射频识别技术[6]和近距离无线通信技术[7],在轨道线路和车体上安置带有里程编码的发射器和接收机,从源头上控制里程偏差。美国国家仪器有限公司设计开发“My RIO-1900”型控制器,在传统里程计数器系统基础上,增加超声波、红外传感器,通过均值滤波与修正,精确测量平台的姿态,并周期性将累计误差清零,达到消除累计误差的目的[8]。在利用数学算法修正里程误差方面,徐鹏提出根据线路上的关键设备信息来修正轨检历史数据里程偏差的思想[9]。秦航远先以台账曲线里程信息为基准进行一次修正,再以速度变化率为依据对轨检数据分段,基于相关系数最大值原则逐点平移滑动匹配进行二次里程偏差修正[10]。汪鑫以平曲线的主点为校正点,基于相关系数和二次插值建立局部波形匹配的里程误差修正算法[11]。与之相似的,还有基于最小二乘匹配算法[12-13]、灰色关联分析技术[14]等修正算法。马萨诸塞大学O’Brien博士根据两次轨检数据的轨距具有高相关性的特点,以范本数据和测量数据之间的互相关函数峰值位置作为基准,利用自回归综合移动平均值时间序列模型和统计线性卡尔曼滤波器等数学原理,建立轨检历史数据里程偏差修正模型[15]。XU[16]提出基于动态时间规划原理(Dynamic Time Warping,DTW),以欧式距离为距离度量指标进行里程偏差修正。

然而,这两类里程误差修正方法尚有不足。(1)在线路中埋设仪器成本高,易损坏。(2)将轨检数据分段,基于相关系数、最小二乘、灰色关联性等原理,以误差为常数逐区段修正里程偏差,但实际上里程误差是一个随机量[17]。经秦航远验证里程误差修正只能控制在3 m左右,修正精度不高[10]。(3)DTW算法存在畸形匹配,会过度拉伸或压缩波形,导致波形失真,而轨道不平顺除幅值外,其波长、波形等特征也是评定轨道平顺状态、诊断轨道病害的重要指标[18]。(4)对于修正效果没有量化评价指标,仅以可视化绘图对比显示。

为提高以超高主点为基准的里程误差修正精度,以波形吻合度最高的两主点区段进行端点对齐,并在此基础上,提出相关性插值优化匹配算法(Correlation Interpolation Optimal Matching Method, CIOM),设置分段数和边界可移量2个尺度参数,动态地移动分段边界,实现点对点的波形匹配,进一步修正区段内采样点随机误差的同时,保留原有波形。最后,针对现有修正算法仅以绘图显示修正效果,无量化评价指标的不足,引入精度因子、形状因子和综合因子作为里程修正结果的量化评价指标,从修正精度、修正前后波形的变化给出评价,完善现有算法评价体系。

1 里程偏差修正算法

为高精度地修正动检数据在里程上的偏差,修正算法共分为两步:(1)基于超高主点的端点对齐;(2)相关性插值优化匹配(Correlation interpolation optimization matching, CIOM)。

1.1 基于超高主点的端点对齐

动检车检测的各项轨道几何参数共用一套里程系统,在空间位置上保持同步。其中,超高数据具有明显的数字折线,其转折点代表特殊形位信息(直缓点、缓圆点、圆缓点、缓直点)[9,12]。因此,可以超高数据的四大主点为里程偏差修正的校正点,实现里程偏差的初略修正。关于特征点的辨识,最为经典的就是道格拉斯普朗克(Dougals-Peucher,DP)算法[19],该算法简单高效,只需找出垂距的最大值便可获得超高主点位置,故本文选取DP算法提取主点里程。

获取主点信息之后,以主点为中心划定波形匹配段,将待修正区段在范本数据相对应的主点附近逐点滑动寻找波形最吻合的位置,如图1所示。以轨向和高低系数之和最大值处滑动的相对距离为里程修正值,进行主点里程修正。

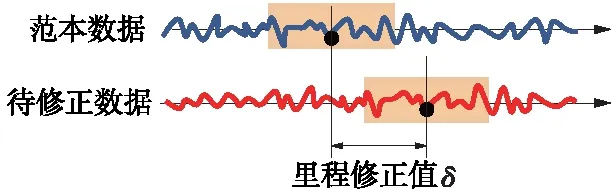
图1 主点里程偏差修正

经验证,以主点区段为基准修正里程误差,仅在主点附近得到精确修正,其他区域仍有较大误差。因此,在主点修正基础上还需进行二次修正,以减小区段内其他采样点的里程误差。

1.2 相关性插值优化匹配算法

假设有2组数据(范本数据X,待修正数据Y),其数据量可不相等。经过主点修正过程,其两端点处已被对齐。范本数据和待修正数据被切分为S段。图2中红色方括号为分段边界。

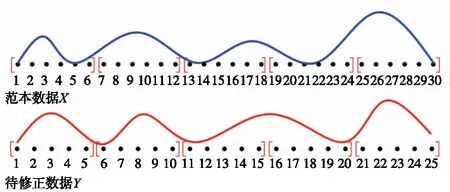
图2 范本数据波形和待修正数据波形

从图2中波形的相对关系来看,待修正区段和相对应的范本区段仅有3种关系。

(1)范本区段的波形较长,包含待修正区段波形特征。

(2)两者的波形特征相对相同。

(3)范本区段的波形较短,被待修正区段波形所包含。

此外,波形相匹配区段之间的数据量可能不相等。图2序号为1～5的待修正区段应该和序号为1～4的范本区段相匹配,但数据量不同,无法计算相关系数,导致与之匹配度最高的为序号1～5的范本区段,间接造成1个采样点的匹配错误,且其具有累积效应,随着匹配区段数增多,匹配错误点越多。

鉴于波形匹配的相对关系和数据量不相等这两个问题,CIOM修正过程主要包含3个步骤:首先将范本数据和待修正数据分段,其次遍历移动分段边界,以至于两者间的波形相对一致;最后分别进行相关性计算,寻找波形的最佳匹配区段。当待修正区段和相对应的范本区段数据量不一致时,对待修正区段进行插值重采样使之与范本区段数据量一致。

图3详细展示图2第1区段的CIOM修正过程。在该例中,范本数据和待修正数据被划分为5段,分段边界的可移动量预设为k∈{-1,0,1},k值为负值表示左移k格,同理,k值为正时,则向右移k格;其次,进行插值以使待修正区段和相应范本区段具有相同数量的数据点;找出两者的最大相关系数Δs(k)

图3 CIOM算法示意(红色为待修正区段,蓝色为范本区段)

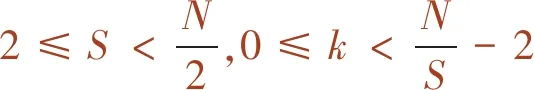
(1)

式中,s表示第s段;ρs(k)为待修正数据的第s段分段边界移动k格情况下的相关系数;Ys为待修正数据第s个区段;Xs+k为边界移动后的范本数据区段;N为待修正数据的数据量;Cov为协方差计算;var为方差计算。

同理,依次从第1区段向后推进同步匹配轨向和高低波形来修正里程偏差。

2 自适应调参

由式(1)可知,除范本数据X和待修正数据Y外,CIOM算法还涉及分段数S和分段边界可移动量k。不断穷举变量以获取最高相关系数的参数组合(S,k)是相当耗时的。因此,有必要探索加速搜索最佳参数组合的方法。

基于某期动检里程数据,计算不同参数组合下修正前后的相关系数,其相关系数的变化趋势如图4所示。不同颜色代表不同的分段数,当分段数S固定时,随着k不断增长,相关系数先提高后趋于恒定,每个分段数变量在k取最大值处取得相关系数最大;分段区段找到最佳吻合位置后,再增加k,相关系数不变。根据这一特点,设计自适应调参过程:首先将预设参数依次排列于网格中,如图5所示,每个网格交点为一组参数组合;然后计算出各分段数在最大可移量行kmax下相应的相关系数,找出最大相关系数所处的分段数Si;在Si列中,计算k由大到小下的相关系数ρ(Si,kj),若计算的后一个相关系数ρ(Si,kj-1)比前一个ρ(Si,kj)小,则停止计算,最佳参数组合便是(Si,kj)。

图4 不同参数组合下的相关性响应

图5 自适应调参示意

如图5所示,设置S∈[10,110],k∈[0,25],根据穷举法需计算2 626次,才能找出最佳参数,而经自适应调参过程最多只需126次,其搜索效率提高95%。

3 评价指标

里程偏差修正的总体目标是使动检数据与范本数据相对齐,同时还保留原有波形特征。因此,偏差修正的评价既要包含对齐的精度,也要包含波形的变化情况。许多学者使用可视化技术绘制里程修正前后的波形叠加图[1,5,10,12,16],该方式操作容易且直观明了。此外,还有利用标准差[17]和相关系数[20]来量化修正前后的效果,但既有指标均未考虑修正前后波形变化情况。丹麦学者Skov提出简易因子和峰值因子,被广泛应用于评估数据集的对齐精度和对齐数据集的形状变化大小[21-23],可作为里程偏差修正评价的量化指标。

(1)精度因子[21]

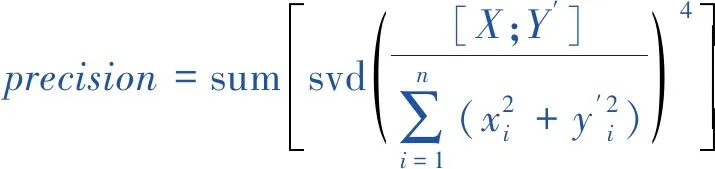
(2)

式中,X为范本数据集;Y′为修正后的数据集;svd为奇异值分解;sum表示对奇异值分解得到的特征值进行加和。精度因子的取值范围为[0,1],其值越大表示对齐的精度越高。

(2)形状因子[21]

(3)

(3)综合因子[21]

综合因子既要包含里程修正的精度评价指标,又要包含修正前后波形的变化大小。因此,综合因子可由精度因子和形状因子加和组成。

(4)

综合因子的取值范围为[0,2],其值越大表示对齐的效果越理想。

4 算法验证及分析

4.1 仿真实验

为验证CIOM算法和评价指标的可靠性和优越性,设置已知误差真值的仿真数据。仿真实验以某期高速铁路实测数据为范本数据,向其中添加已知误差以模拟待修正数据,再分别利用CIOM算法、最小二乘匹配LSM[15]、动态时间规划DTW[19]作偏差修正对比实验,各算法修正前后的波形如图6所示,将3种算法在波峰(波谷)特征点处的里程修正值与已知误差真值作差,统计差值的平均值AVG,并绘制里程残余误差图,见图7。

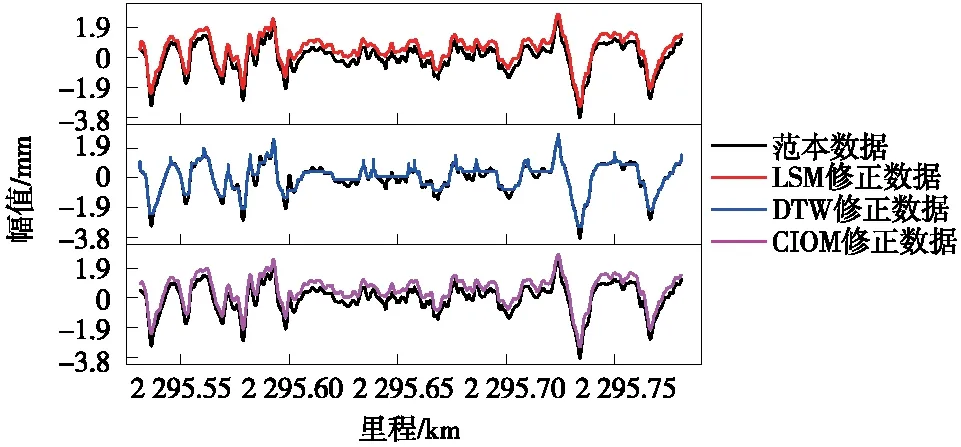
图6 各算法修正后的波形对比

图7 里程残余误差

图7显示DTW、CIOM、LSM三种算法修正后残余里程误差,其平均值分别为0.03,0.07,0.19 m,DTW修正精度最高,随后依次是CIOM、LSM。但图6从可看出:DTW算法过度拉伸或压缩了原有波形,导致波形不光滑,而CIOM和LSM则保留原有波形的特征。基于式(2)和式(3)计算3种修正结果的评价指标,其结果见表1,DTW的精度因子最高,为0.975,但其形状因子最低,为0.70;CIOM的精度和形状因子均优于LSM。评价指标和绘图显示的结果相一致,既反映了评价指标的有效性,又证明了CIOM的优越性。

表1 3种修正算法的评价指标

4.2 工程检验

以某高速铁路2019年1月7日的检测数据为范本数据,用来修正其他时期动检数据的里程偏差。对各期动检数据依次进行主点对齐一次修正和CIOM二次修正。图8给出相邻两主点之间的一次修正和二次修正的修正效果对比,基于主点进行里程修正,其里程误差仅在主点附近区域得到精确控制。两主点之间仍存在较大误差,里程差可达到4.75m。经过CIOM修正,其精度因子由0.63提高到0.97,两者波形高度对齐,证实了CIOM算法能有效消除两主点间域的里程误差。

图8 CIOM修正效果对比

图9绘制CIOM修正前后的高低、轨向局部波形对比图,为定量评估修正效果,统计了不同日期不同区段的修正数据与范本数据差值的标准差、相关系数,各评价指标取平均值,见表2。图9和表2可知:经CIOM修正后,同里程范围内的各期检测数据波形相对齐;各期的精度和形状因子均可达到0.9左右;较差标准差较之前降低了,相关系数可达到0.9,修正后波形高度吻合,说明对于不同时间不同区段的里程误差修正,CIOM也是行之有效的。

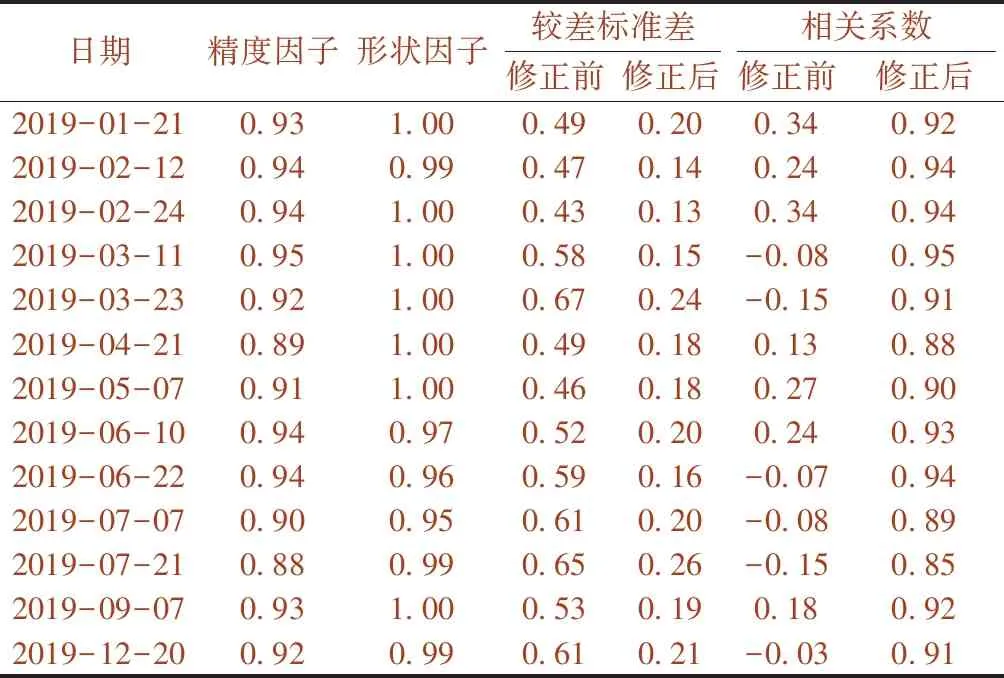
表2 不同日期的CIOM修正结果统计分析

图9 不同日期的CIOM修正效果

为对比3种算法的性能,基于式(2)、式(3)、式(4)计算2019年1月21日各算法的每公里修正指标,其结果见图10。无论高低或轨向,DTW修正后的精度因子均最高,平均值可达到0.98;其次是CIOM,其精度因子平均值为0.90;LSM最低。但在形状因子方面,DTW远低于CIOM、LSM,CIOM和LSM的形状因子均接近于1。

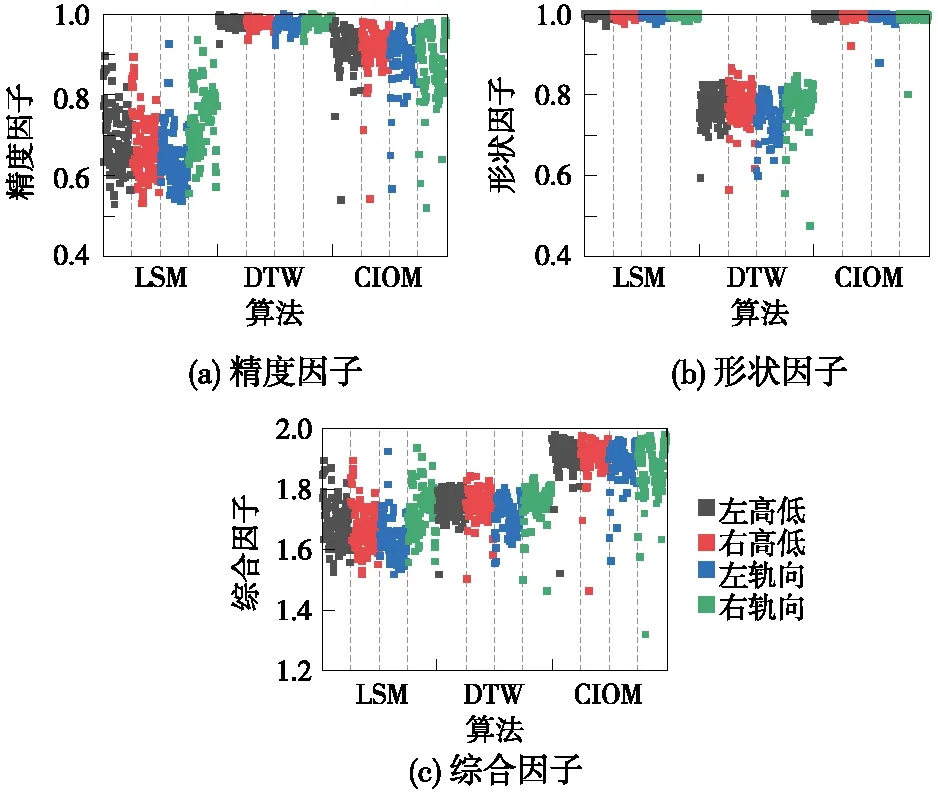
图10 各算法的评价指标对比

综上所述,CIOM算法优于DTW和LSM,其可弥补LSM修正精度不足和DTW会改变原有波形的缺点。

5 结论

针对动检数据之间存在里程偏差问题,考虑到误差的随机性并尽量保留原有波形,提出CIOM算法,在精确修正里程误差的同时,保留原有数据的波形,并引入精度因子、形状因子、综合因子作为里程偏差修正评价指标,完善里程误差修正的评价体系。经与现有的LSM和DTW算法对比实验,主要结论如下。

(1)CIOM算法里程偏差修正后,不仅两主点间的里程误差得到精确控制,波形的吻合度也得到提高,CIOM可将里程残差控制在0.07 m左右。

(2)CIOM算法不仅精确修正了里程误差,还保留了原有波形特征,其精度因子和形状因子均可达到0.9左右。此外,CIOM算法弥补了LSM修正精度不足和DTW会改变原有波形的缺点。

(3)精度因子可反映两期轨检数据的对齐精度,形状因子可弥补现有评价指标无法评估波形变化情况的不足。