强激光场驱动的原子里德堡态激发及电离(特邀)
2023-08-21赵勇周月明
赵勇,周月明
(华中科技大学 物理学院,武汉 430074)
0 引言
超快超强激光技术最近几十年发展迅速。目前已得到的最短激光脉宽已经在50 阿秒(Attosecond, as,10-18s)以下[1],得到的激光聚焦后峰值强度能达到1022W/cm2以上[2]。在微观世界中,分子的转动在皮秒(Picosecond, ps, 10-12s)量级,原子核的振动在飞秒(Femtosecond, fs, 10−15s)量级,而电子的运动在阿秒量级。超快超强激光技术为探索原子分子微观结构乃至内部电子的运动规律、操控电子行为提供了一种重要手段。在强激光的作用下,原子分子会被电离,进而诱导许多有趣的非线性物理过程,比如阈上电离(Above Threshold Ionization, ATI)[3-9]、非次序双电离(Non-sequential Double Ionization, NSDI)[10-12]和高次谐波产生(High-order Harmonic Generation,HHG)[13-16]等。在过去几十年中,这些强场过程引起了人们的广泛关注。
强激光场驱动的原子分子电离是强场物理中的许多超快现象的第一步,也是许多研究关注的重点。随着激光强度和激光波长的变化,原子发生电离的机制也各不相同。如图1 所示,原子在激光场中的电离机制大致可分为单光子电离(Single-Photon Ionization, SPI)、多光子电离(Multi-Photon Ionization, MPI)、隧穿电离(Tunneling Ionization, TI)和越垒电离(Over-Barrier Ionization, OBI)[17]。在强场电离中,人们通常使用Keldysh 参数[18](也叫绝热参数)来区分占主导的电离机制,其中,Ip表示电离势,Up=F2/4ω2表示电子在激光场中的有质动能,ω和F分别表示激光的频率和电场振幅。当γ≫1 时,原子主要发生多光子电离,此时激光强度较小,电子通过吸收多个光子跃迁到连续态而电离。当γ≪1 时,隧穿电离占主导,此时激光强度较大且激光频率较小,被激光场压低的势垒相对静止,电子主要通过隧穿到连续态而发生电离。而当γ~1 时,电子处于多光子电离和隧穿电离的过渡区,两种电离机制同时存在,目前实验室的激光条件大多处于这个区域。特别地,当激光强度大于越垒电离的电离阈值,且激光频率足够小时,原子将主要发生越垒电离。Keldysh 参数只是区分主导的电离机制的一个大致参考参数,在实际情况中,上述的电离机制之间并没有绝对明确的界限。

图1 原子在强场中的电离机制示意图Fig.1 Schematic diagram of the ionization mechanisms of atom in strong laser field
原子与强激光场作用,除了发生上述电离,实验还观测到相当大一部分电子布居到激发态上,形成中性里德堡态原子[19-23]。里德堡态原子具有诸多特殊性质,比如极大的轨道半径和超长的寿命等,因此,里德堡态原子在物理学和信息学上的很多方面有着广泛的应用,例如超快精密测量[24]、量子非线性动力学[25]、长程多体相互作用[26-27]和量子信息操纵[28-29]等等;除此之外,被强激光场驱动的里德堡态原子还能被人们用来研究中性粒子加速[30-34]、探究多光子拉比振荡(Rabi oscillation)[35-38]、理解光电子谱特征[39-40]和产生近阈值谐波[41-42]等等。但是,里德堡态原子在强场中的激发和电离过程中还存在许多尚未解决的问题,例如里德堡态激发机制及其对激光参数的依赖,里德堡态上的电子波包的干涉,里德堡态原子在圆偏光中电离的圆二色性等。人们对此展开了大量研究,对这些问题都有了较深刻的认识。本文将介绍这些方面的最新研究进展。
如无特别说明,全文均使用原子单位制(Atomic units, a.u.)。该单位制下,电子质量和电荷量me=|e|=1,普朗克常数h=2π。
1 里德堡态原子的强场激发机制
与强场中的电离机制相似,在强场里德堡态激发中,人们也提出了两种完全不同的激发机制。如图2所示是两种不同激发机制的示意图。图2(a)是多光子共振激发[43-50],基态能级和能移后的高激发态能级的能量相差整数倍光子能量,基态电子通过能级间的Freeman 共振[51-53]跃迁到里德堡态上;图2(b)是相干重捕获激发,也被称为受挫隧穿电离(Frustrated Tunneling Ionization, FTI)[54-55]。在隧穿区域,一部分隧穿电子在电场中未获得足够大的能量,在返回原子或者分子核附近时被核的库仑势捕获到里德堡态轨道上,形成里德堡态原子[56-65]或者分子[66-72]。虽然这两种强场激发机制提供的物理图像和相关推论已经各自在理论和实验上得到了验证,但是里德堡态激发究竟是通过多光子共振还是FTI 机制,仍然是一个充满争议的问题。
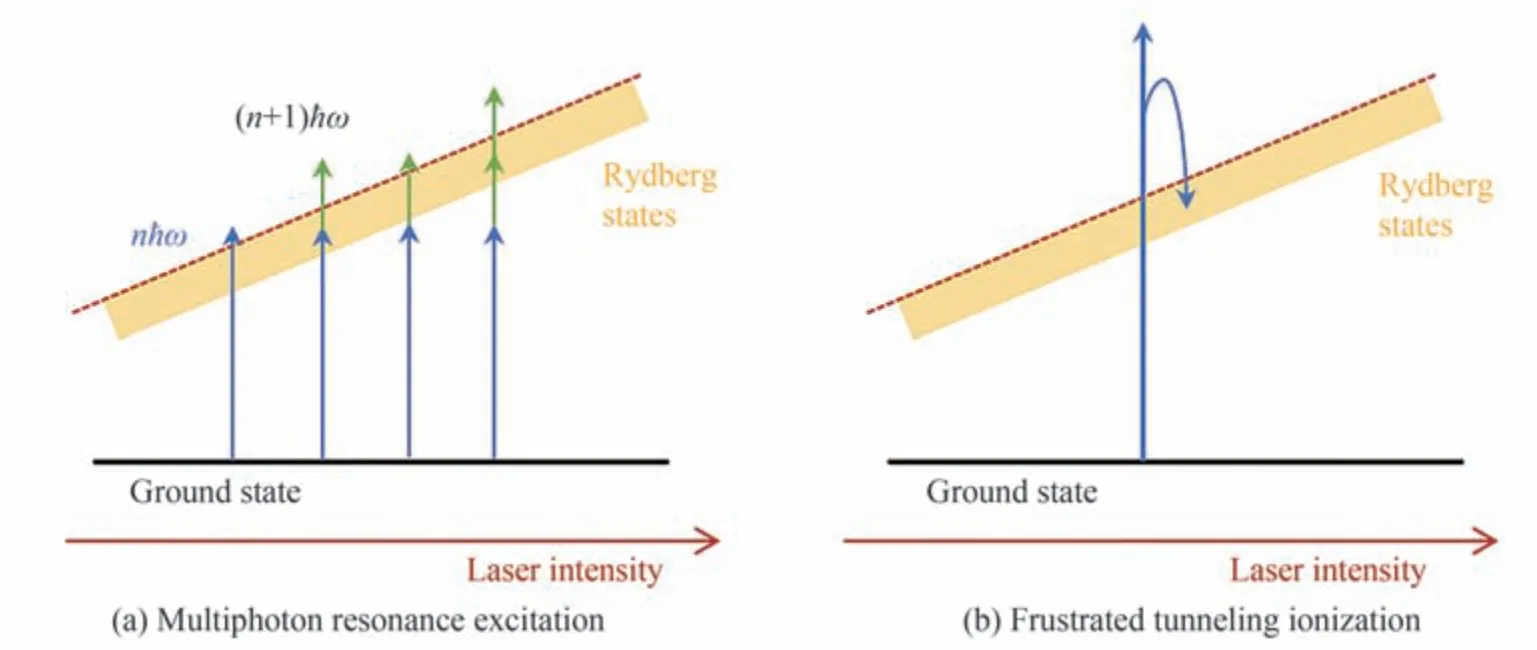
图2 里德堡态原子的两种强场激发机制示意图Fig.2 Schematic diagram of two strong-field Rydberg state excitation mechanisms
1.1 多光子共振激发
在多光子共振激发的研究中,早在1992 年,DE BOER M P 和MULLER H G 在实验上观测到大量电子在激光结束后存活在里德堡态上[19],与之前研究看法不同,他们认为,多光子电离中激发和电离是分两步进行的,基态电子首先通过Freeman 共振跃迁到能移后的里德堡态上,然后在接下来的脉冲时间内,里德堡态电子被持续电离到连续态。因为高里德堡态对电离具有很强的稳定性,不容易被电离,因此,在脉冲结束后,仍有大量的电子留在里德堡态上,实验上对光电子谱共振峰的测量也证实了这一点。
随后,JONES R R 等研究Kr 和Xe 在强场中的多光子电离时[20],也发现了大量的中性里德堡态原子,以及带电的里德堡态离子,他们认为这些里德堡态粒子来自于基态电子与ac-Stark 能移后的中间态的共振,研究发现,即使在饱和电离的光强下,这些高里德堡态粒子仍然很难被电离,证明里德堡态电子在强场中有很强的电离稳定性。之后,大量的研究在实验和理论上进一步探究了强场粒子的里德堡态激发过程[73-74]。
2014 年,LI Q 等通过数值求解含时薛定谔方程(Time-Dependent Schrödinger Equation, TDSE),在理论上深入研究了氢原子的多光子电离与激发过程[44]。如图3(a)所示,电离率和激发率随光强的变化曲线呈现出周期性的振荡,其振荡周期的光强间隔为一个光子能量,这明显是多光子电离通道关闭(channel closing)的特征,因此,他们认为激发是由于能级间的多光子共振导致的。另一个证据是在光电子能谱上,随着光强增大,ATI 峰会向能量更小的方向移动,表现为图3(b)所示的斜条纹,而斜条纹与水平轴的交点,正好是ac-Stark 能移效应预测的多光子电离通道关闭的光强阈值,如图中黑色箭头标记。当ATI 峰被移动到电离阈值之下时,基态与高里德堡态发生共振,激发率上出现峰值,同时,能谱上出现共振峰。此外,研究还发现,角量子数越大的里德堡态,在强场中越稳定,越难被电离。随后人们对强场多光子激发展开了进一步的研究[45-48,75-77]。ZHANG W 等2019 年在实验上证实了在400 nm 激光场中,H2分子强场电离中产生的里德堡态碎片是通过多光子共振路径产生[47]。

图3 电离率、激发率和光电子能谱随激光强度的变化[44]Fig.3 The ionization, excitation probabilities and photoelectron energy spectrum as a function of the laser intensity[44]
2020 年,CHETTY D 等在实验上进一步测量了Ar 原子在30 fs 和6 fs 激光脉冲下,电离率和里德堡态产率随光强的变化[78],如图4 所示,结果显示,里德堡态产率随光强增大确实表现出周期为一个光子能量间隔的振荡,但是产率增强并不是之前所说的通道关闭效应导致的,而是来自于基态和能移后的高激发态之间的Freeman 共振。因此,脉宽越大时,基态与高激发态的共振就越强,振荡则越明显,在6 fs 的短脉冲下,振荡几乎消失。多光子共振激发机制的研究中仍然存在一些问题和谜团,这有待人们更加深入地研究和探索[49-50]。

图4 Ar 原子的单电离产率与里德堡态产率随光强的变化[78]Fig.4 Yields of singly ionized and excited Ar atoms as a function of laser intensity [78]
1.2 受挫隧穿电离激发
在相干再捕获激发机制的研究中,WANG B B 等很早就意识到,在深隧穿区域的里德堡态激发,可能是由于隧穿电子被核的库仑势捕获到里德堡态上导致的[54]。2008 年,NUBBEMEYER T 等在实验上测量到了800 nm 光驱作用下产生的氦原子里德堡态产率极其随椭偏率的变化,并提出了受挫隧穿电离(FTI)机制[55]。该激发机制的物理图像与重散射中的三步模型类似,分别是:第一步,电子隧穿通过被电场压低的势垒,到达连续态形成自由电子;第二步,隧穿出去的一部分电子在激光场的作用下被拉回母核离子附近;第三步,返回母核离子附近的一部分电子被母核的库仑势捕获到激发态的轨道上,形成中性里德堡态原子。NUBBEMEYER T 等利用改进后的飞行时间质谱仪,直接测量了里德堡态原子的产率,如图5(a)所示,在隧穿区域,实验测量的里德堡态原子产率要比理论计算结果高几个数量级,因此必然还存在额外的激发通道,也就是FTI 激发通道。为了证明该机制的正确性,他们在实验上测量了He+离子和He*里德堡态原子的产率随激光椭偏率的变化,如图5(b)所示,随着椭偏率的增大,里德堡态原子的产率比单电离率更快下降到零,这正是重捕获模型所预计的特征,实验结果强有力地支持了FTI模型。在理论计算中,利用FTI模型计算出的里德堡态原子主量子数n分布,也与量子模型的结果一致,峰值都在n=6~10附近,理论结果再次证明了FTI模型的正确性。

图5 He 原子的电离率和里德堡态原子产率随光强和椭偏率的变化[55]Fig.5 The yield of ionized and excited He atoms as a function of the laser intensity and ellipticity[55]
FTI 模型在重构里德堡态原子的主量子数n分布等方面取得了巨大的成功,也吸引人们对里德堡态原子展开了大量的研究[79-81],例如中性里德堡态原子在激光场中的加速、电离稳定化等。而且FTI 的经典轨迹模型,在揭示和理解激发过程的动力学细节上起到了很大的作用。2012 年,LIU Yunquan 等[40]发现FTI过程中的重散射步骤不再是必要的,电子可以直接发射到里德堡态轨道上,同时里德堡态原子具有很强的局部稳定性;而且实验测量和理论计算都发现,FTI通道的存在会导致光电子动量谱上的低能电子部分产率降低。
里德堡态原子在强激光场中能够表现出很强的电离稳定性。2013 年,EICHMANN U 等对里德堡态原子的稳定化进行了进一步的研究[57],实验显示,被第一束脉冲激发的里德堡态He 原子,在加入第二束脉冲激光后,仍然有大部分电子留在里德堡态上而未被电离,只有靠近核附近的、能量较小的一小部分里德堡态电子被电离,同时大量的里德堡态电子被重新布居到离核更远、能量和角动量更大的激发态轨道上,而这部分里德堡态电子在强场中具有非常强的电离稳定性。
2015 年,ZIMMERMANN H 等通过改进质谱仪,在气体束与激光相互作用区上下加入一对高压铜极板,对里德堡态原子进行逐步静电场越垒电离和直接探测,在实验上测量并重构出了He*原子的主量子数n分布,如图6 所示[58]。此外,该实验对He 原子的自旋状态高度敏感,在无外电场情况下(铜极板上的电压在脉冲结束后打开),高l激发态(l>2)的三重态和单重态互相混合,偶极近似和LS 耦合并不严格有效,因此,基态电子被激发到混合态上后,除了大部分通过自发辐射回到单重态的基态上(1s2),还有少部分电子会衰退到三重态的亚稳态上(1s2s),该亚稳态非常稳定,其寿命大于毫秒量级,且激发能大于微通道板(Microchannel Plate, MCP)的功率阈值5 eV,因此这部分亚稳态的He*(1s2s)原子可以直接被MCP 探测到,而且探测效率非常高。而在外电场一直存在时(铜极板上的电压在脉冲前打开),单重态和三重态会分离,单重态基态电子激发后不能衰退到三重态亚稳态上,因此探测效率大大降低,大约只有1%。该工作为研究原子自旋耦合提供了新的思路。前文已经提到,里德堡态原子在静电场中的越垒电离阈值为FOBI=1/3n5,因此,通过在铜极板上逐步施加对应n值的电压,即可测量出剩余里德堡态原子的产率,然后重构出主量子数n的分布,结果如图6(b)所示,实验数据和理论计算的n分布的峰值都在n=9 附近,两者符合得非常好,这再次证明了FTI模型的正确性。该研究为在实验上探测里德堡态原子的能量分布提供了新的方法和思路。
1.3 从多光子激发到FTI 的过渡
强场里德堡态激发的两种机制各有实验数据支持。2017 年,ZIMMERMANN H 等在实验上测量了Ar和Ne 原子的里德堡态产率随光强的变化[82],这是首次在实验上跨越如此大的光强范围,光强从多光子电离区一直增强到隧穿电离区。如图7 所示,分别展示了400 nm 和800 nm 激光脉冲下的结果,实验结果和TDSE 结果符合得很好。在400 nm 激光下,Ar 原子的激发率在6 光子电离通道关闭的光强附近出现一个明显的台阶结构,激发率迅速上升;在Ne 的多光子通道关闭光强附近也出现明显的振荡结构,研究发现该激发增强现象是由于基态与高激发态之间的强共振导致的,而且该台阶状结构与激发模型无关,因此有望成为一种校准光强的方法。随着光强增大,激发过渡到隧穿区域,光强平均效应导致产率振荡消失。在800 nm激光下,由于聚焦空间平均效应和脉冲能量的抖动,产率的振荡被抹去,激发态产率平滑上升。本工作首次研究了原子从多光子激发到FTI 激发的过渡。
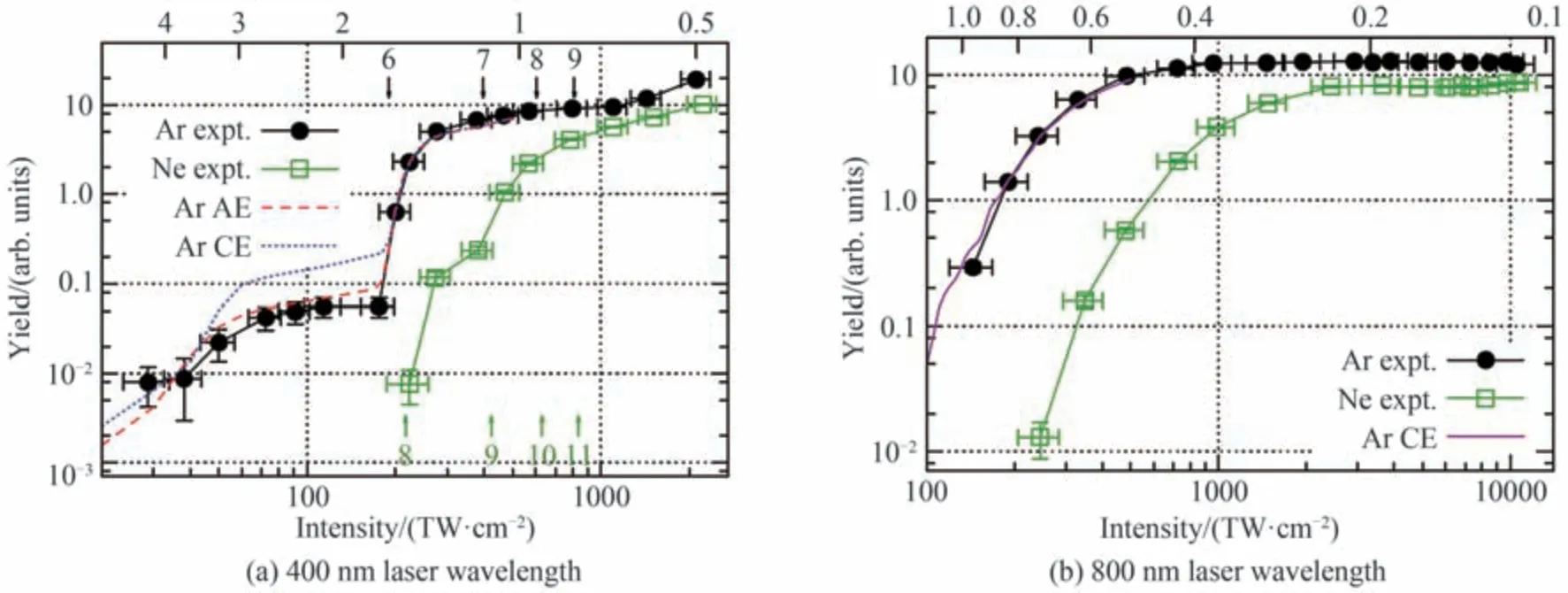
图7 Ar 和Ne 的里德堡态产率随激光强度的变化,上轴是Keldysh 参数[82]Fig.7 Yield of strong-field excited Ar and Ne atoms as a function of the laser intensity. The Keldysh γ parameter for argon is shown on the upper x axis[82]
最近,XU S 等在前人的研究基础上,实验上更加精密地测量了Ar 的里德堡态产率和电离率随激光强度的变化[83],如图8 所示,分别展示了400 nm 和800 nm 激光脉冲下的结果。通过改进实验技术,他们降低了测量光强的误差,得到了光强间隔更小、更精确的实验数据。在400 nm 激光下,里德堡态产率出现两个台阶装结构,6 光子电离通道关闭处的里德堡态产率和电离率同时上升,在7 光子电离通道关闭处激发态产率的极大值却对应于电离率的极小值。在800 nm 激光下,里德堡态产率与电离率表现出相位相反的连续振荡,电离率的极大值对应激发率的极小值,通过一种带相位的强场近似模型计算,表明该振荡是由于不同激光周期隧穿的FTI 电子之间的干涉引起的,该计算表明反相位振荡对应FTI 激发机制,而400 nm 下的同时上升对应于多光子共振激发机制。该研究揭示了强场激发机制从多光子共振激发到FTI 激发机制的过渡,提供了更加完整的强场激发图像。
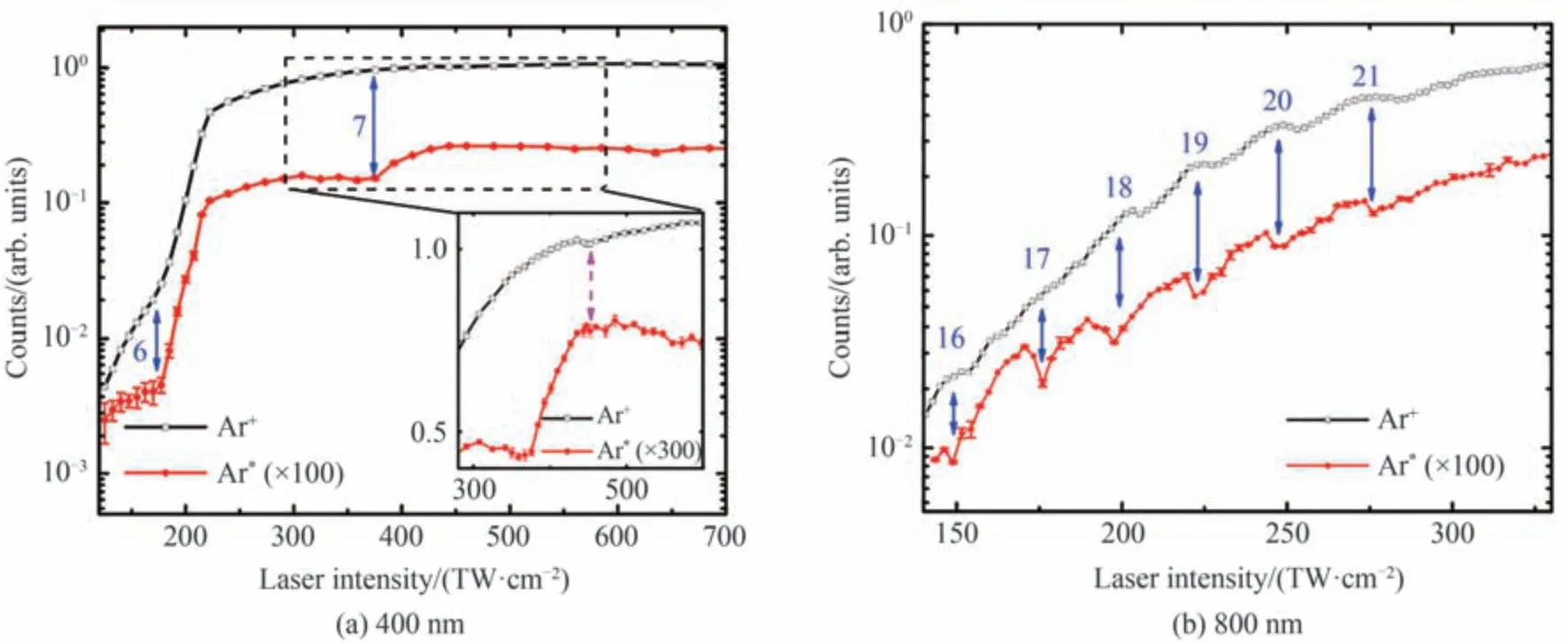
图8 实验测得的Ar+离子和激发态原子Ar*的产率随激光强度的变化,激光波长分别为400 nm 和800 nm[83]Fig.8 The measured intensity dependence of the yields of ions Ar+ and excited atoms Ar∗and the laser wavelengths are 400 nm and 800 nm, respectively[83]
2 激光脉冲对激发过程的调控
激发到里德堡态上的电子会布居到不同的激发态能级上,形成不同的产率分布和量子数分布,这些特征分布对理解激发过程、电离稳定化、电离通道关闭和激光场的空间梯度影响都有着重要作用,而里德堡态原子的产率和量子数分布受到激光脉冲参数的显著影响,最近几年,大量研究探索了激光脉冲对激发过程的调控,并取得突出进展。
2.1 里德堡态产率对激光椭偏率的依赖
在FTI 中,激发被描述为电子隧穿再捕获的过程,因此,里德堡态产率对激光椭偏率有很强的依赖,即激发率会随着椭偏率的增大而急剧下降。首次提出FTI 机制的NUBBEMEYER T 小组在实验上直接测量了He 原子的单电离率和激发率随激光椭偏率的变化曲线[55],如图5(b)所示,随着椭偏率的增大,He 的激发率比电离率更快地下降到零,该实验数据说明隧穿区的激发过程确实是一种重散射过程,从而证明了强场激发里德堡态的机制是FTI。
FTI 图像描述的是隧穿电子主要在电场力作用下的运动过程,因此,FTI 过程非常适合用经典轨迹模型来进行描述。忽略库仑势的作用,LANDSMAN A S 小组基于SFA 模型推导出了强场里德堡态的产率公式[84],公式显示,激发率只与激光的光强、波长以及粒子的电离势有关。如图9 所示,根据公式画出的里德堡态产率随椭偏率的变化和实验结果符合得很好。因为在推导过程中,忽略了库仑势都对电子运动轨迹的影响, 因此结果只适用光强远大于库仑势的情况。
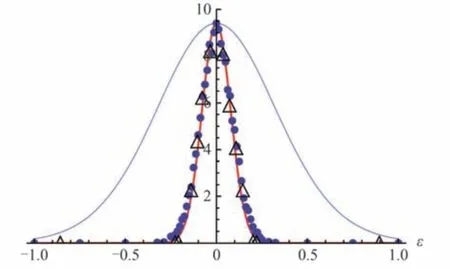
图9 解析曲线(红色曲线)、模拟计算结果(蓝色圆)和实验数据(黑色三角)得到的氦原子里德堡态产率随椭偏率的变化,蓝色曲线表示He+的总电离率[84]Fig.9 Analytic curve(red line), simulations(●) and experimental data(△)for the Rydberg yield of Ar as a function of the ellipticity, and total ion yield of He+ is shown on the same plot (blue line)[84]
对于低光强下的情况,库仑势的作用将不可忽略。FU Libin 小组通过求解三维经典方程,并考虑到库仑势的作用,模拟计算了不同激光参数和目标气体的FTI 过程[85]。计算发现,Mg 原子在光强为I=0.04 PW/cm2时,里德堡态产率随椭偏率的变化曲线不再是之前的单峰高斯分布,而是变为双峰分布,即激发率在小椭偏率下出现一个极大值,如图10(a)所示。而且,FTI 电子在初始隧穿时间和初始横向速度窗口中的分布形状对初始条件十分敏感,比如初始位置r0,会显著影响里德堡态产率对激光椭偏率的依赖关系,如图10(e)所示,当电子的初始位置在离核更近的地方时,里德堡态产率曲线上的双峰现象更加明显。

图10 Mg*产率随椭偏率的变化曲线,及其在初始条件平面内的分布[85]Fig.10 The dependence of Mg* yield on ellipticity, and the distribution in initial tunneling coordinates[85]
FTI 电子在初始条件坐标系内的分布形状决定了里德堡态产率随椭偏率的变化趋势,因此,可以通过控制激光参数,改变FTI 电子在初始条件平面内的分布形状,进而调控里德堡态原子的产率。如图11 所示,利用经典轨迹蒙特卡洛系宗模型,计算了不同激光强度与波长下,Ar 原子FTI 过程中里德堡态产率随椭偏率的变化曲线[86]。计算结果表明,当波长为800 nm,光强为8×1013W/cm2时(曲线a),Ar 原子的里德堡态产率对椭偏率表现出反常依赖,即在椭偏率为0.2 附近出现一个极大值,而不是以往研究中的单调下降,反而和FU Libin 小组发现的Mg 原子激发率对椭偏率的依赖关系比较相似,这种产率的反常增强现象在其他两组激光条件下却没有出现。对FTI 电子轨迹的追踪发现,正是因为FTI 电子在初始条件坐标系内的半圆环状分布导致了其产率对激光椭偏率的反常依赖。进一步的计算表明,FTI 电子的分布形状与激光脉冲的波长、光强和脉宽均有关系。因此,通过改变上述激光参数,可以实现对里德堡态原子产率的调控。
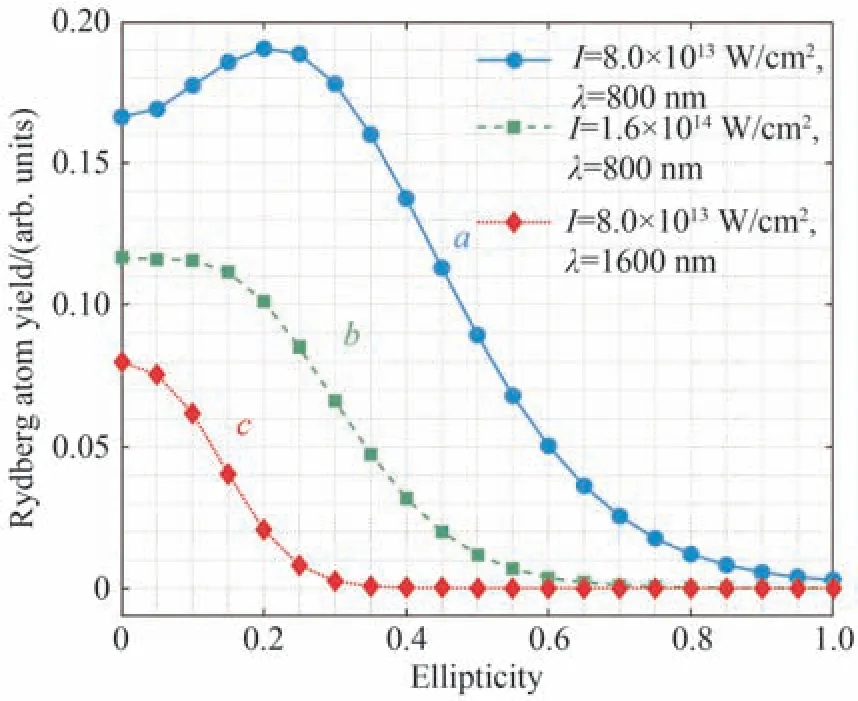
图11 里德堡态原子的产率随着椭偏率的变化[86]Fig.11 The yields of excited atoms as a function of the ellipticity of the laser pulses[86]
人们通常认为,里德堡态原子的产量对激光椭偏率的依赖关系是判断里德堡态原子的产生机制是多光子共振激发还是受挫隧穿电离的依据。但是,这种判断并不可靠。对于多光子共振激发,里德堡态原子的产率也会随着椭偏率的增加而迅速减少。而在非绝热隧穿电离区域,受挫隧穿电离得到的里德堡态原子产量,随着椭偏率的增加,并不一定迅速下降,反而可能出现反常的产率增加现象。这两种机制并没有明显的界限。
经典轨迹方法总是存在一定的局限性,它在某些激光参数范围内的结果将不再准确。PAULY T 小组随后使用了单电子近似(Single Electron Approximation,SAE)的含时薛定谔方程(Time-Dependent Schrödinger Equation,TDSE)方法和含时R矩阵全电子重头算方法(RMT)来验证和比较以前研究中的里德堡态产率随椭偏率的变化曲线,结果如图12 所示,SAE 的结果介于LANDSMAN A S 的结果和ZHAO Y 的结果之间,但并没有发现ZHAO Y 等预测的在椭偏率为0.2 附近的极大值;但同时发现,4 s 态的产率在椭偏率为0.1 附近出现了极大值。上述结果说明,不同近似方法和模型计算出的里德堡态产率存在差异,在某些激光参数范围,某些模型将不再适用。但是,目前还没有实验结果表明,Ar 原子的激发率不存在对椭偏率的反常依赖,这有待进一步的实验来验证。

图12 不同理论方法计算得到的激发率随椭偏率的变化曲线[63]Fig.12 Variation curves of the excitation yield with ellipticity calculated by different theoretical methods[63]
2.2 激光脉宽对主量子数的调控
之前的研究表明,增大激光脉冲的脉宽,激光与原子相互作用时间变长,电离率自然会上升,导致里德堡态原子的产率下降。在隧穿区域,利用激光脉宽可以实现对里德堡态产率和主量子分布的调控。ORTMANN L 小组利用CTMC 模型研究了激光脉宽对FTI 的影响[87],结果表明,随着激光脉宽的增大,里德堡态原子的总产率急剧减小,同时,主量子数n分布的峰值将向能量增大的方向移动。图13 是FTI 电子在初始条件坐标系内的主量子数n分布随激光脉宽的变化,可以看到,n分布呈环状分布,随着脉冲周期数的增加,FTI 电子从内环开始消失,也就是从n较小的区域开始减少。通过对FTI 电子轨迹的分析发现,不同n值电子的轨道周期不同,因此绕核一圈返回核附近的时间不同,n值较大的电子轨道周期时间更长;如果电子在返回核附近时激光脉冲还未结束,那么电子将在库仑势和激光场的共同作用下电离,因此,随着激光脉宽的增加,里德堡态电子将从n值较小的部分开始电离。因此,利用激光脉冲的脉宽,可以对里德堡态原子的主量子数n分布进行调控。
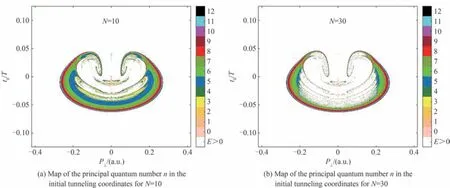
图13 FTI 电子的主量子数n 分布对电离时间t0和初始横向动量P⊥的依赖关系,N 表示激光脉冲包含的光周期数Fig.13 Map of the principal quantum number n depending on the ionization time t0 and the initial transverse momentum P⊥ which the pulse duration is given by the number of cycles N
2.3 激光光强、波长以及相位的影响
在强场实验中,光强是一个相对容易控制的参数,光强对激发与电离调控的研究比较丰富。根据ac-Stark 能移效应,在激光电场中,原子的电离阈值和能级将随着激光包络一起移动,因此,随着光强增大,多光子电离通道将周期性的被移动到电离阈值之下,导致电离率随光强出现周期性振荡,这就是众所周知的channel-closing 效应,据此可以在实验上校准光强。同时,激发态能级由于能移,也会与基态周期性产生共振,随着光强增大,能级上移,更低的能级被移动到共振位置,因此,随着光强增大,里德堡态原子的主量子数分布的峰值将会向低能方向移动,如图14 所示,里德堡态原子的n分布随光强增大表现出斜向下的条纹。利用光强,可以实现对里德堡态原子产率和能量分布的调控。

图14 氢原子激发率、电离率和n 分布随光强的变化;垂直虚线表示多光子通道关闭的光强,旁边的数字表示电离所需的最少光子数Fig.14 The ionization yield, excitation yield and n distribution as a function of the laser intensity. The vertical dashed lines indicate the intensities at which the ionization channel closes. The numbers near the vertical dashed lines indicate the minimum photon number required for multiphoton ionization of H
同理,激光频率决定了光子的能量,改变激光频率将影响能级间的共振,共振能级上的布居将被增强,因此,通过改变波长可以调控里德堡态原子的主量子数分布。同时,利用特殊频率的两种正交场,可以控制电子波包的干涉,进而提取出电离过程的一些高精度信息,为探测原子内部结构及电子运动提供工具。
3 里德堡态中的干涉
干涉现象在量子力学主导世界中,是普遍存在的。在强激光场与原子分子相互作用过程中,电子波包之间的干涉是探测电离动力学过程的重要方法,人们通过各种各样的干涉图案来提取电离动态过程。人们在强场电离的研究中发现,干涉除了广泛存在于电离电子的动量谱中,在原子的里德堡态上也存在大量的干涉现象。这些干涉现象通常表现为产率随激光强度产生周期性振荡。根据振荡周期的光强间隔对应的能移大小,我们将干涉分为三类。
3.1 振荡周期ΔUp=ℏω 的干涉
在很早以前,人们就在强场多光子电离中发现,电离率会随着激光强度的增加发生周期性振荡,其振荡周期的光强间隔对应的能移正好为一个光子能量(ΔUp=ℏω),根据ac-Stark能移效应,人们将该振荡理解为电离阈值移动引起的多光子电离通道关闭[82-83,88-89]。后来,人们在里德堡态激发中也发现了这种振荡。在多光子区域,人们一开始认为该激发率的振荡是由于ATI峰随光强增大,移动到电离阈值之下导致的,如图3(b)所示[44]。最近,CHETTY D 等在实验上证实了里德堡态产率上的振荡峰不是由于channel closing 导致的,而是由于ac-Stark 能移导致的基态电子与高激发态的Freeman 共振导致的,周期性的共振导致了这种周期性的振荡[78]。如图5(b)所示,通过增大激光脉宽,可以使频谱变窄,共振增强,里德堡态产率上的振荡峰则更加明显,如图中脉宽为30 fs 的曲线所示。
但在隧穿电离区,FTI 半经典模型并不能很好地解释这种里德堡态产率随光强的周期性振荡,而TDSE量子模型虽然包含了所有的量子效应,但不能很好地帮助人们理解激发过程的细节。2019 年,HU Shilin 等提出了一种基于强场近似的量子轨迹模型[90],如图15(a)所示,该模型很好地解释了里德堡态产率随光强振荡的问题。图中灰色虚线表示激光电场,价电子在某一个光学半周期通过隧穿发射出去,被捕获到里德堡态上的电子具有不同的相位差,它们之间相互干涉导致光强依赖的产率振荡,同一方向的轨迹的干涉周期为ΔUp=ℏω,不同方向的电子轨迹的干涉导致的振荡峰间隔为ΔUp=2ℏω。该量子模型很好地复现了TDSE 中的所有特征和结果。同时,其与实验上测得的Xe 原子里德堡态产率随光强的振荡也符合得很好。该模型在隧穿区域提出了带相位的量子轨迹模型,同时具备经典轨迹的激发细节和量子模型的干涉效应。

图15 基于强场近似的量子模型(QM)的示意图,以及里德堡态原子产率随激光强度的变化[90]Fig.15 The schematic picture of the Quantum Model (QM) and the Rydberg-state population as a function of the laser intensity[90]
3.2 振荡周期ΔUp ≫ℏω 的干涉
在2017 年,PIRAUX B 等在研究H 原子的强场电离与激发动力学过程时,发现在长波长激光脉冲下(1 800 nm),H 原子里德堡态产率随激光强度出现一种明显的周期性振荡[91],如图16 所示,其振荡周期的光强间隔为ΔI=50 TW/cm2,这远远大于channel closing 效应预测的一个光子能量的间隔ΔI=2.2 TW/cm2,显然不是channel closing 效应引起的,他们推测这是一种拉曼过程,但遗憾的是,TDSE 并不能帮助他们得到清晰的物理图像和细节。同时,半经典FTI 轨迹模型不能复现这种振荡结构,激发率只会随着光强平滑地变化,这说明该现象明显超出了半经典图像的理解范围。因此,一种考虑到电子与核之间的库仑相互作用的量子轨迹模型,对于在长波长条件下理解这种振荡背后的物理机制是十分必要的。
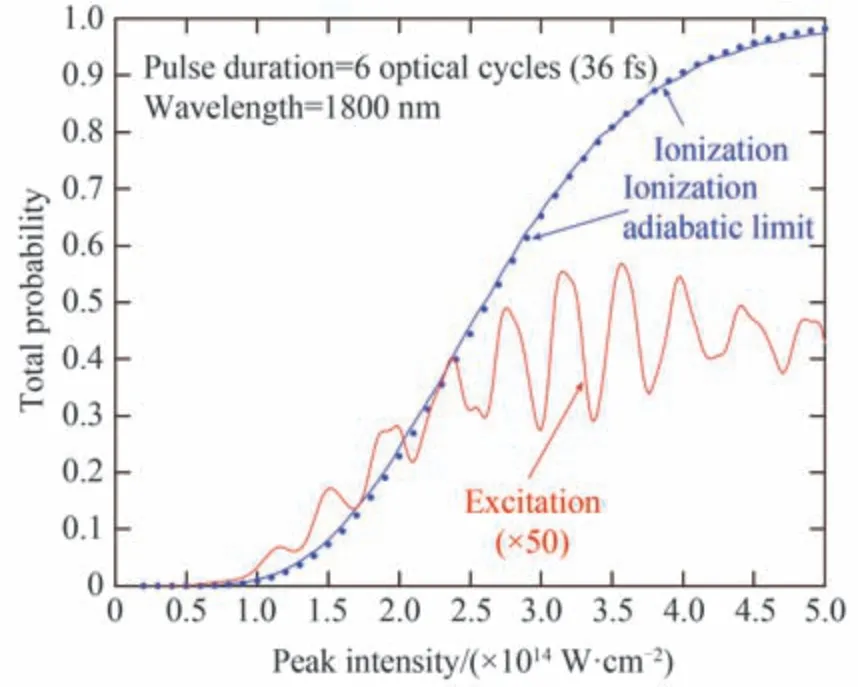
图16 H 原子电离率和里德堡态产率随激光强度的变化[91]Fig.16 Total probability of ionization and excitation of atomic hydrogen as a function of the peak intensity[91]
最近,LIU Mingqing 等在2019 年提出的量子轨迹模型基础上,加入重散射项来描述电子与核之间的库仑相互作用,将强场里德堡态激发理解为一个相干散射重捕获的过程[92]。如图17 所示,计算结果很好的复现了TDSE 的结果,里德堡态的产率随激光强度出现一个周期为ΔI=50 TW/cm2的振荡结构,并且进行聚焦光强平均处理后的结果与实验数据也符合的非常好。该模型描述了这样一种物理图像,当隧穿电子在不同时刻返回核附近时,在核库仑作用下发生前向散射,从而改变电子的运动轨迹,同时导致光电子谱上的低能结构(Low-Energy Structure, LES)。此外,部分散射电子会被重新捕获到里德堡态上,这些不同返回时刻的电子轨迹之间的干涉,导致里德堡态产率随光强出现振荡,其振荡周期远大于一个光子能量。进一步地,他们还推导了干涉振荡周期与波长的关系,振荡周期与λ-1.2成正比。对于800 nm 波长,因为振荡周期太大而被其他振荡所掩盖,所以在实验上无法测量。

图17 考虑散射的量子轨迹模型的计算结果[92]Fig.17 Calculated results of the quantum trajectory model considering scattering [92]
3.3 振荡周期ΔUp<ℏω 的干涉
除了上述两种干涉,人们还在强场激发和电离中发现了一种新的时域双缝干涉,被称为动态干涉[93-106],具体表现为电离率或者里德堡态产率随光强增大出现的周期远小于一个光子能量(ΔUp<ℏω)的振荡。动态干涉是激光脉冲包络引起的ac-Stark 能移导致的,其示意图如图18(a)所示,高激发态能级和连续态会随着脉冲包络一起移动,基态电子将在某个时刻和能移后的高激发态产生共振,根据包络形状,满足共振条件的时刻有两个,对称分布在脉冲包络的上升沿和下降沿,由于相位不同,这两个通道发射的波包之间会相互干涉,这相当于一种时域双缝干涉。动态干涉将导致激发率和电离率随光强产生周期性振荡,其振荡周期对应的光强间隔小于一个光子。动态干涉也叫Stückelberg 振荡[107],早在一个世纪前就被提出,后来被人们广泛研究[51,108-114]。
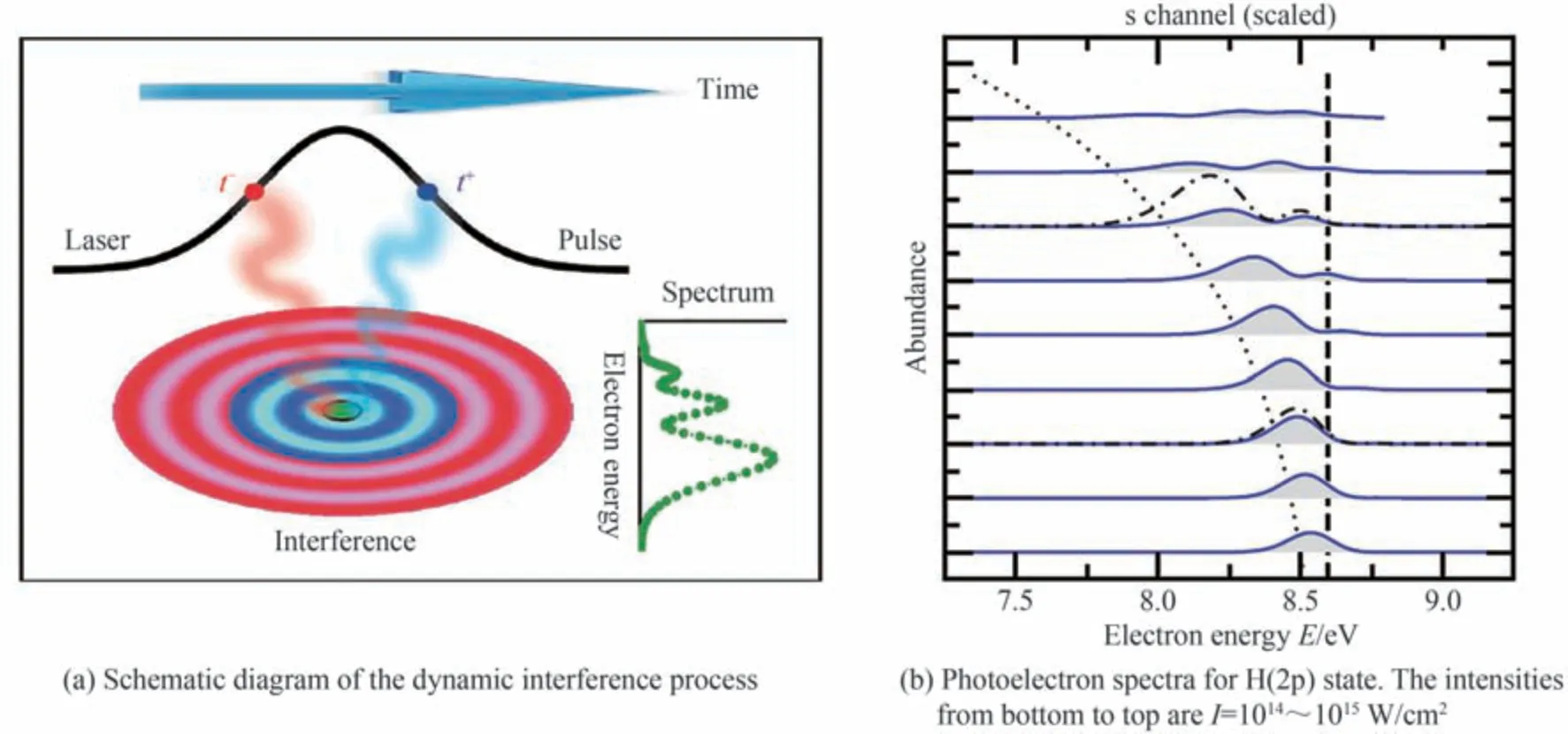
图18 动态干涉过程示意图[97]以及H 原子2d 态的电离能谱[102]Fig.18 Schematic diagram of the dynamic interference process[97], and the photoelectron spectrum for H(2p) state[102]
1995 年,JONES R R 等首次在实验上观测到电离信号上的动态干涉振荡现象[115],他们利用未聚焦的激光脉冲电离Na 原子束,在不同光强位置探测离子产率,从而避免了光强平均效应的影响。如果考虑光强平均效应,电离信号上的振荡将被抹平。JONES R R 等测量多光子共振的电离信号,间接证明了里德堡态上也存在动态干涉。
随着XUV 激光技术的发展,人们发现,在单光子电离的能谱上也存在动态干涉现象[93-94,97],如图18 所示,传统ATI 能谱上的单峰被多峰结构所代替。DEMEKHIN P V 等在2012 年首次提出动态干涉的名称和概念[97],但他们的推导并没有考虑到初态的电离耗尽效应。如果光强过大,初态将在脉冲达到峰值前被电离耗尽,下降沿上的电离通道将会被关闭,动态干涉也就不会出现。BAGHERY M 等2017 年推导了动态干涉的必要条件[102],加入了电离耗尽效应的影响,并预测H 的2p 激发态将出现动态干涉,如图18(b)所示。与此同时,原子的稳定化会阻碍初态的电离耗尽,使得基态原子在高光强下出现动态干涉成为可能[116]。在过去十几年,动态干涉引起了人们的广泛研究[103-106,117-126],但在实验上的直接测量仍未实现。
直到2022 年,BENGS U 等通过一种全光测量的方法,在实验上直接观测到Ar 原子里德堡态上的动态干涉现象,如图19 所示,被激发到里德堡态上的电子会发生自发辐射放出荧光,通过测量荧光的光谱和对应的光强,便可以得到相应里德堡态上的产率,图19(a)是三个里德堡态衰变放出的荧光强度随激光强度的变化,可以看到其随光强出现明显的振荡结构,实验结果与TDSE 和双能级模型的计算结果完全吻合,证明了该全光测量方法的可行性,但是该方法受到衍射光栅和通光孔径的限制。该工作表明,动态干涉振荡可以作为一种灵敏的测量工具来观测里德堡态上的动力学过程。
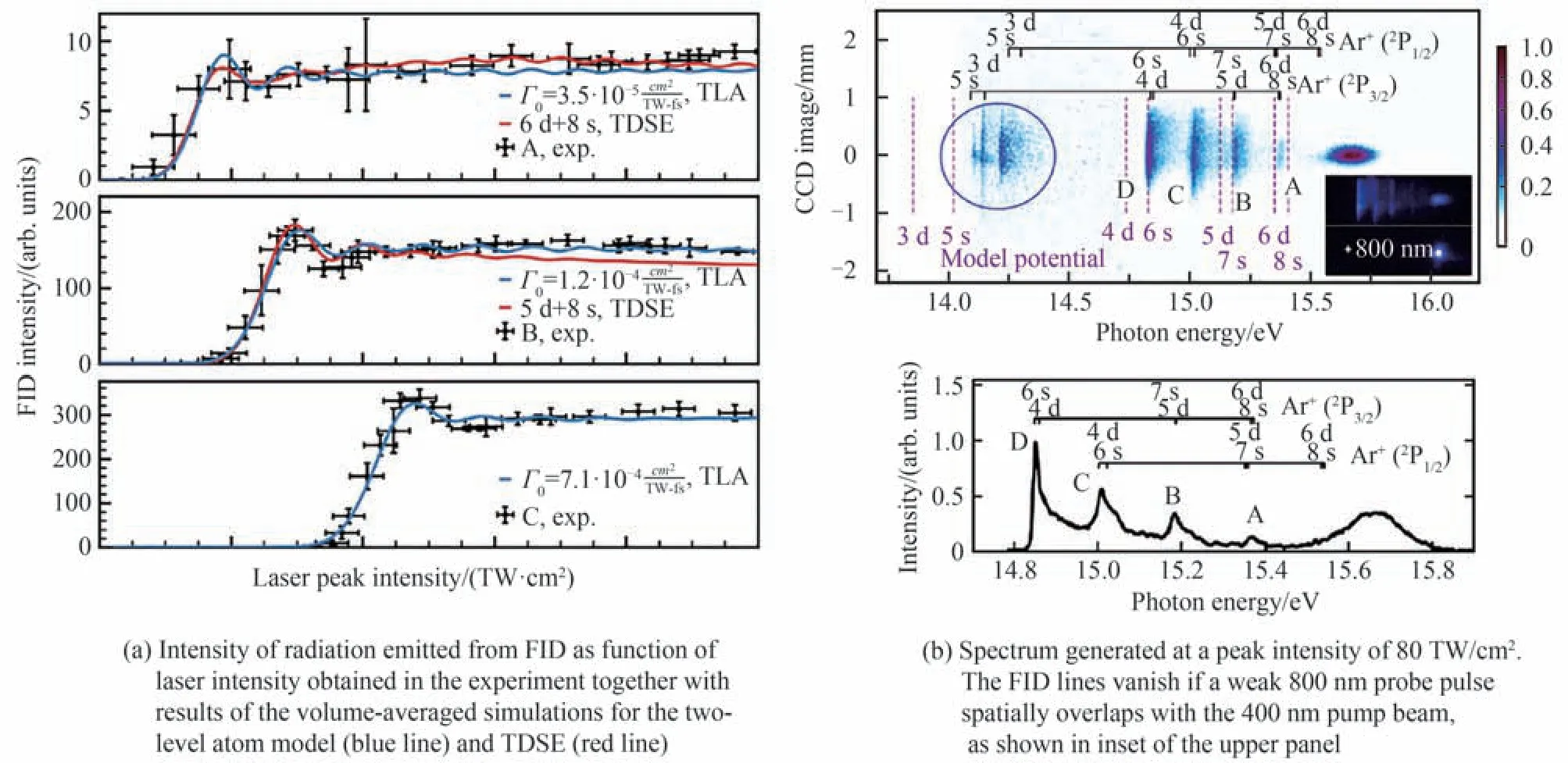
图19 实验测得的里德堡态产率和荧光光谱[127]Fig.19 Intensity of radiation emitted from FID as function of laser intensity obtained in experiment [127]
在长波长区域,高光强引起的巨大ac-Stark 能移允许激光脉冲包络的上升沿上能存在多条激发通道。通过数值求解三维含时薛定谔方程,我们研究了氢原子强场多光子激发中里德堡态的动态干涉。在400 nm激光脉冲下,计算发现,当光强增大到八光子电离区域时,干涉振荡周期突然变大。经分析,由于电离耗尽效应,高光强下初态会在脉冲达到峰值前就被电离完全耗尽,脉冲下降沿上的激发通道被关闭;但巨大的ac-Stark 能移使上升沿上能容纳更多的激发通道,它们之间仍能产生干涉。干涉通道的改变导致了振荡周期突然变大;同时,奇偶宇称通道的同时存在将导致光电子动量谱沿激光偏振方向表现出明显的上下不对称性。利用里德堡态的动态干涉,观测到光强增大时初态的耗尽以及激发通道的变化。
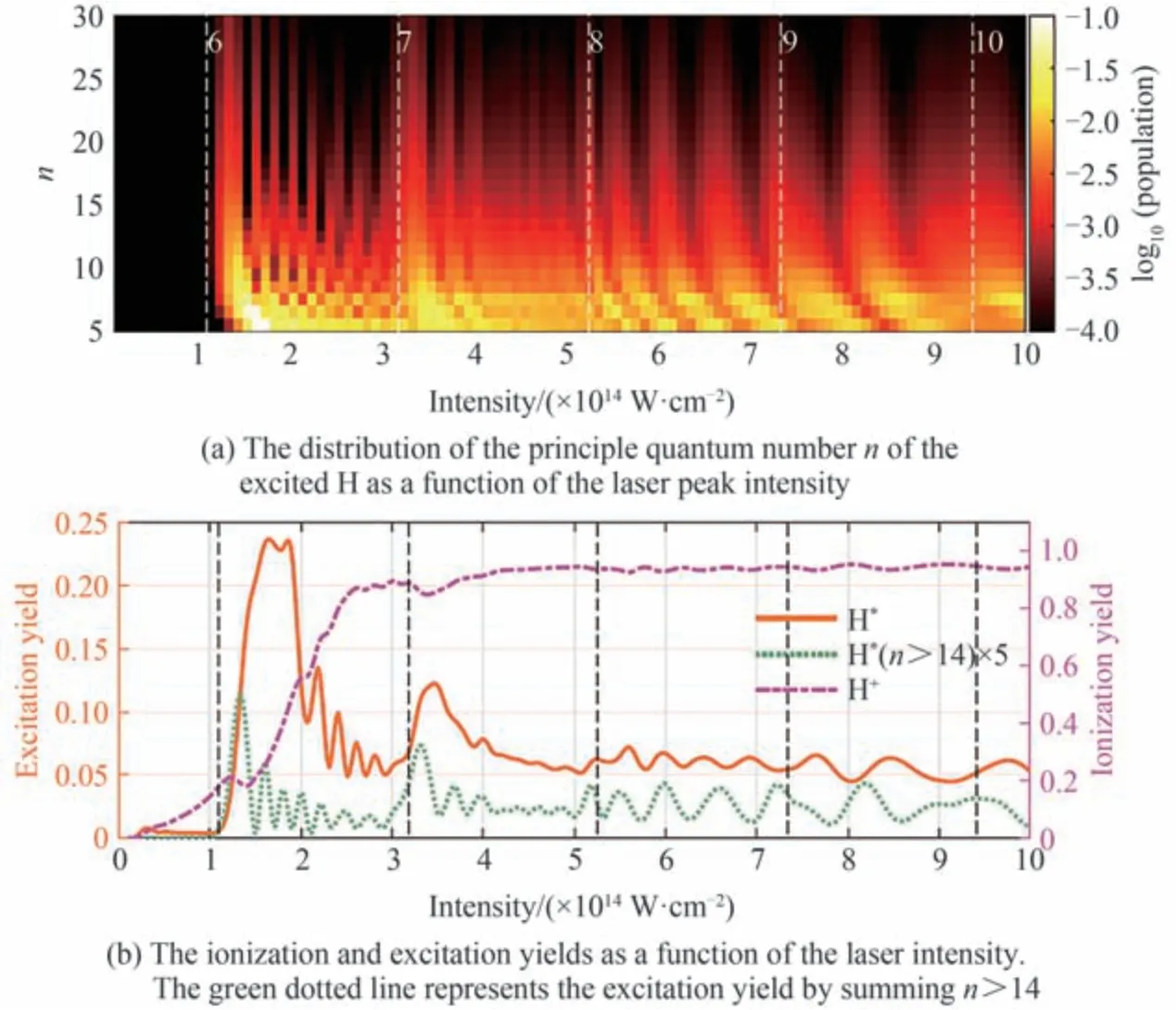
图20 里德堡态氢原子的主量子数n 分布、激发率和电离率随光强的变化 [128]Fig.20 The distribution of the principle quantum number n, excitation yield and ionization yield as a function of the laser peak intensity[128]
4 里德堡态原子强场电离的圆二色性
里德堡态原子在强激光场中表现出很强的电离稳定性[129-130],因此,被激发到高能级的电子在后续激光脉冲中很难被电离,在激光脉冲结束后能存活在里德堡态上,从而被观测到。里德堡态原子的电离稳定化在过去十几年引起了人们的广泛关注[57,131],研究发现,能量越大、能级越高、角动量越大的里德堡态原子越容易出现电离稳定化,越难被激光脉冲电离。
圆偏光存在手性,其中一个特征就是其在与物质相互作用时会导致镜像对称性破缺,这种有趣的现象也被称为圆二色性(Circular Dichroism, CD),它的表现之一是在定向排列的双原子分子甚至是基态原子的单光子电离中,吸收相反螺旋性的光子导致的光电子角分布(Photoelectron Angular Distributions, PADs)的差异。然而,对于非手性目标粒子,吸收相反螺旋性的光子仅仅会导致它们是彼此的镜像(忽略宇称破坏效应)。因此,只有当目标粒子也拥有手性时,这种镜像对称性才会被破坏。手性分子,即不能与它们自己的镜像重叠的分子,是一种典型的不对称目标粒子;即使是随机取向的分子,它们在强场中吸收单光子或多光子的电离过程也可以表现出明显的圆二色不对称性。这种不对称的光反应具有深远的意义,有助于解决长期以来与地球生命相关的氨基酸和糖类分子的同手性之谜。
原子并不具有严格意义上的手性,但当其轨道角动量的沿光束传播方向极化时,也就是说磁量子数m≠0,结合外部的圆偏激光场和光子的自旋,整个系统也能表现出手性,这种系统手性也被称为“外部手性”。原子结合圆偏光作为最简单的手性系统,非常适合用来理解手性光与手性物质相互作用的不对称性。对于偶极跃迁,吸收一个左旋或者右旋的光子,会使磁量子数增大1 或者减小1,因此,极化原子电离的手性依赖可以理解为末态不同分波的叠加和干涉,从而导致最终电离率和PADs 的不对称性。尽管光电子能谱上的圆二色性移动非常小,但它对理解缀饰态原子的内部结构、提取原子环流态的特征具有重要意义。
近年来大量研究报道了圆里德堡态原子在圆偏激光中电离的圆二色性,圆里德堡态指m取最大值的激发态,为了方便描述,本文把价电子环流方向与圆偏光电场旋转方向相同的情况叫做同向旋转,反之则叫做反向旋转,本章节研究的正是同向与反向旋转情况下里德堡态原子电离的圆二色性,也叫做电离对磁量子数符号依赖的研究。
众所周知,在多光子电离区域,同向旋转的电子比反向旋转的电子电离得更快,这在很多教材上都被提及,对于圆里德堡态在圆偏微波场中的电离,情况也类似,同向旋转的情况下电离率更大,特别是当电子轨道的角速度与激光场的角速度大小相同时,电离率达到最大值。但是,在非绝热隧穿区域,情况则完全相反,与电场反向旋转的电子更容易发生隧穿,从而被圆偏光更有效地电离,如图21 所示,展示了Kr 原子p±轨道上的电子在右旋圆偏光中发生非绝热隧穿电离的情况,可以看到,在非绝热隧穿区域,相当大光强范围内,p-轨道电子的电离率更大,变化激光频率,参数越靠近非绝热隧穿条件,两者的电离率差异越大,圆二色性越明显;在光电子能谱上,p-轨道电子的电离峰更高,而且电离峰更靠近低能方向。该工作首次在理论上证明了非绝热隧穿电离过程中的圆二色性。
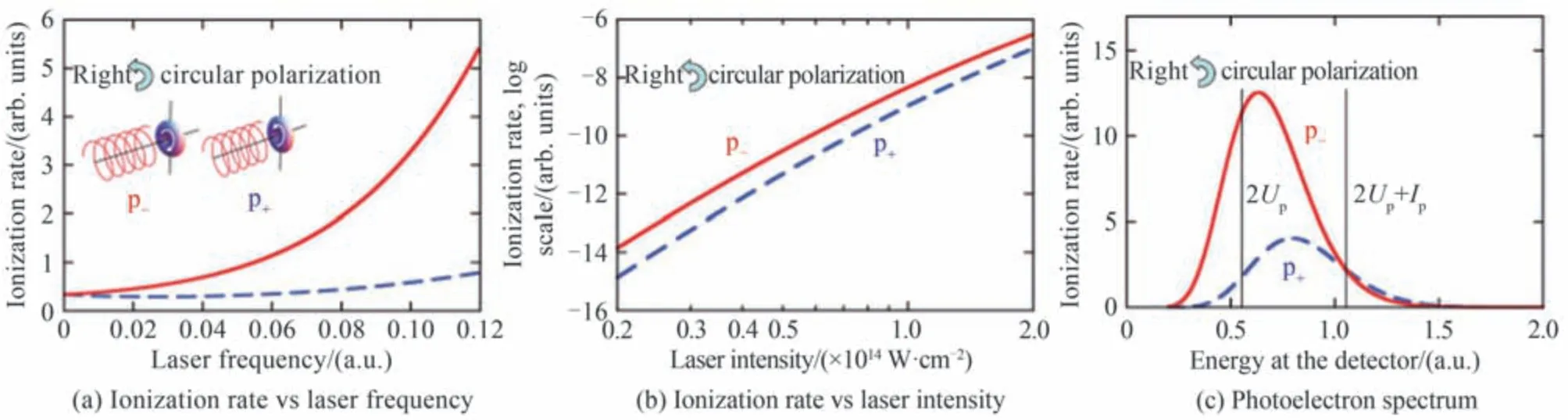
图21 Kr 的p±轨道在右旋圆偏光下的电离率[132]Fig.21 Ionization rate for p± orbitals in right circular polarization laser field[132]
2012 年,HERATH T 等首次在实验上观测到隧穿区域同向与反向旋转电子的电离率存在差异[133],但是无法区分到底是哪种情况下的电子电离率更大。之后,大量关于强场电离的圆二色性的实验与理论研究被报道。直到2018 年,ECKART S 等通过泵浦探测技术与高分辨动量测量,在飞秒尺度上制备了单原子环流态,并测量了环流态在非绝热隧穿电离过程中的圆二色性[134]。环流态的电离率和光电子动量谱对磁量子数m的符号表现出明显的依赖性,其能谱和PADs 表现出明显的不对称性,实验结果与理论计算结果一致。
在MPI 区域,大量的研究显示圆二色性与光强有很大关系,同时ac-Stark 能移引起的Freeman 共振会导致电离被选择性增强,这使得MPI 区域的圆二色性特征更加复杂。ILCHEN M 等在2017 年用近红外光(Near-Infrared, NIR)加极紫外光(Extreme Ultra-Violet, XUV)的双色光实验证明[135],He+(3p)在MPI 中同向旋转电子的电离率更大,如图22(a)所示,此外,圆二色性(表征为CD=(P+-P-)/(P++P-),P+表示同向旋转电离率,P-表示反向旋转电离率)会随着NIR 光强的增大而逐渐减小并变号,他们将CD 的下降解释为NIR 光强增大引起的旋向依赖的He+(3p)态的ac-Stark 能移,从而导致同向旋转的电离率P+的下降,但是这种解释并不完全正确。2019 年,GRUM-GRZHIMAILO A N 等通过求解TDSE,在理论上重新研究了这种圆二色性的变化[136],他们发现,同向旋转情况下增强的NIR 光破坏了XUV 光对He+(3p)态的泵浦激发,从而导致电离率迅速下降,于是圆二色性在小光强范围内迅速变化,共振在多光子电离过程中扮演了十分重要的角色。

图22 原子少光子电离示意图[137]Fig.22 Scheme for sequential ionization of few-photon ionization[137]
在2021 年,DE SILVA A H N C 等在实验上采用一种近共振的全光激光原子阱(All-optical laser atom trap, AOT)技术,避免了里德堡态制备被破坏,将Li 原子的泵浦激发效率提高到了93%[137],而且泵浦光与探测光存在一定的时间延迟,这样避免了以前工作中探测光对泵浦激发过程的破坏,从而大大提高了实验的信号强度与探测精度。如图22(b)所示,除了测量到Li 原子的强圆二色性外,他们还发现,当探测光频率接近共振频率时,共振导致的旋向依赖的AT 分裂(Autler-Townes splitting)也能在能谱上被分辨出来。该研究有助于在飞秒时间尺度和极小能量分辨率(meV)上利用可逆开关产生自旋极化电子脉冲。
在研究氢原子在圆偏光中电离的圆二色性随激光频率的变化过程中,我们发现,对于圆里德堡态原子的单光子电离,当激光频率在初态能级与低能级共振附近时,同向旋转情况下的电离率曲线上会出现新奇的电离增强和电离抑制现象[138-139],如图23 所示。分析表明,由于偶极选择定则,同向旋转电子和低能级发生近共振时导致电离增强;而在中心共振频率,初态能级与低能级之间会产生拉比振荡,抑制里德堡态原子的电离。因此,通过改变激光频率,我们可以实现对里德堡态原子电离圆二色性的调控,但单单改变激光频率对圆二色的调节范围始终有限。进一步,通过在共振频率调节光强和脉宽,我们实现了对圆二色性的大范围调控,如图24 所示,随着光强增大,CD 大幅下降并变号,该方法为制备自旋极化脉冲提供了一种思路。
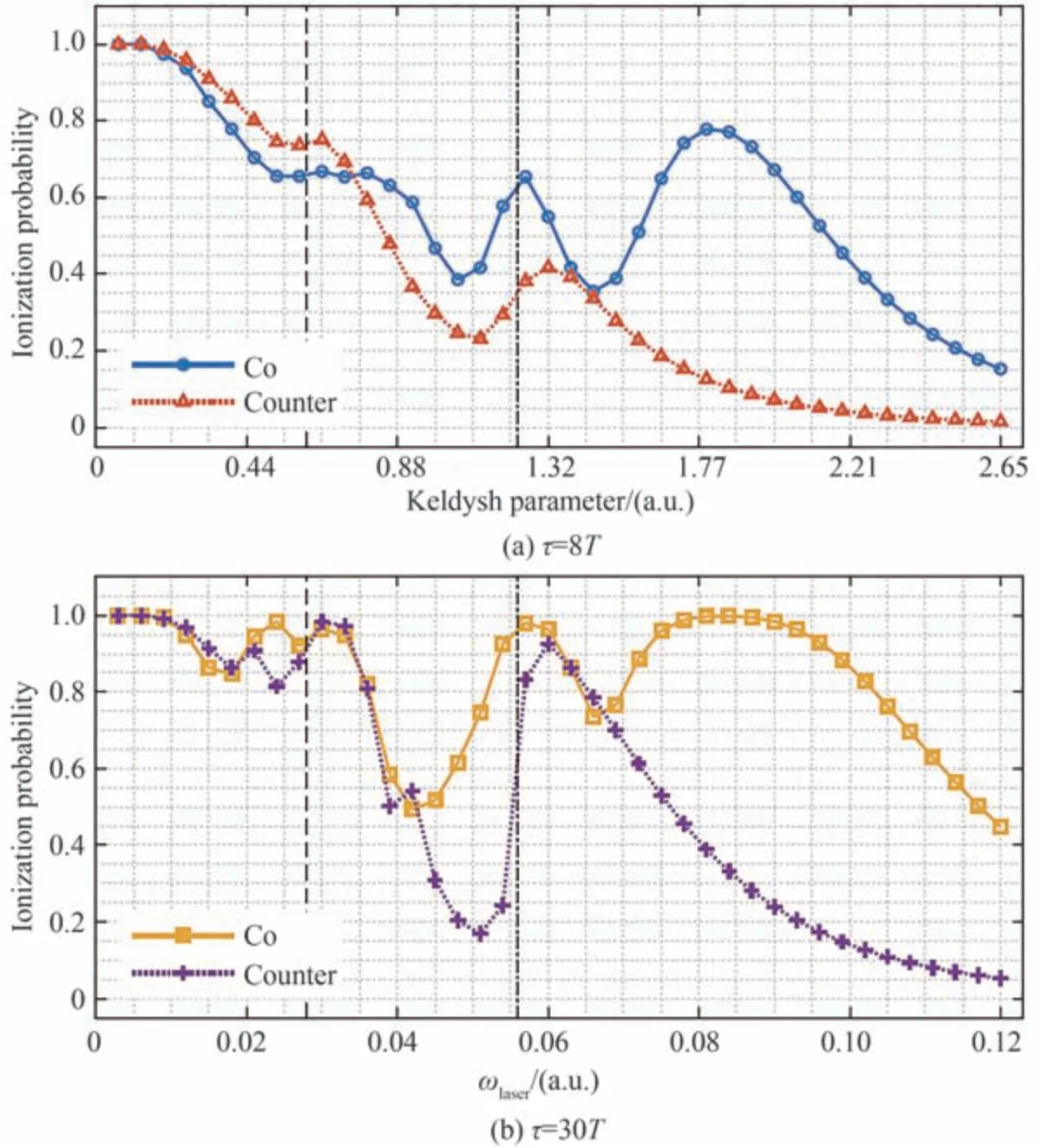
图23 两种初态氢原子的电离率随激光频率的变化,垂直虚线和点划线分别表示双光子和单光子电离的电离阈值,激光强度均为8×1012 W/cm2[139]Fig.23 The ionization probabilities of two initial states of hydrogen atoms as a function of the laser frequency. The vertical dashed and dashed-dotted lines indicate the two- and one-photon ionization thresholds, respectively. The laser intensity is 8×1012 W/cm2 [139]

图24 里德堡态氢原子电离圆二色性随光强的变化,激光脉冲处于共振频率ω=0.066 a.u.Fig.24 The ionization probabilities of H Rydberg states as a function of laser intensity. The frequency of laser is ω=0.066 a.u.
5 结论
本文介绍了近年来超快超强激光脉冲驱动的原子里德堡态激发及电离的最新研究进展。强场里德堡态激发有两种机制,一种是多光子共振激发,基态电子通过多光子共振被激发到里德堡态上;另一种是FTI激发,隧穿电离的电子在返回核附近时被库仑势捕获,形成里德堡态原子。通常认为里德堡态原子的产量对激光椭偏率的依赖关系是判断里德堡态原子的产生机制是多光子共振激发还是受挫隧穿电离的重要依据。但是,这种判断并不可靠。对于多光子共振激发,里德堡态原子的产率也会随着椭偏率的增加而迅速减少。而在非绝热隧穿电离区域,受挫隧穿电离得到的里德堡态原子产量,随着椭偏率的增加,并不一定迅速下降,反而可能出现反常的产率增加现象。这两种机制并没有明显的界限。最近的实验,通过测量里德堡态原子的产量和单电离的离子产量随激光强度的变化,观察到了激发机制从多光子到FTI 的过渡。
近期的实验观察到了强场里德堡态原子产生中的干涉现象,表现为里德堡态原子产量随着激光强度的振荡。根据振荡周期的光强间隔对应的as-Stark 能移大小,这些干涉现象分为三类。第一类是周期为一个光子能量的干涉。在多光子共振激发图像下,这种干涉可以被理解为通道关闭效应。在隧穿图像下,可解释为不同半周期隧穿的电子波包产生的干涉。第二类为周期远大于一个光子能量的干涉,该干涉通常出现在长波长区域,来自于不同时刻发生近前向散射(捕获)的通道之间的干涉。第三类为周期远小于一个光子能量的干涉,它是激光包络导致的两侧激发通道引起的干涉。
具有较大轨道角动量的里德堡态原子在圆偏光作用下的电离表现出了很强的圆二色性。因为这种圆二色性,可以把里德堡态作为最简单的手性系统,对人们探索分子的手性具有重要意义。此外,里德堡态原子的圆二色性对制备和探测超快时间尺度下的高纯度单一环电流态、产生自旋极化电子脉冲等也具有重要意义。
在描述强激光与原子分子相互作用时,通常用到了电偶极近似。这是因为激光的波长比原子分子的电子分布空间尺度大很多,因此,电偶极近似能够很好地描述强激光与原子分子相互作用的过程。这种近似对于人们理解强场中的原子分子超快动态过程带来了便利。但是,最近的原子分子强场电离实验,测量到了许多非偶极效应导致的新现象,例如,光电子能量对发射角的依赖,光电子沿激光传播方向的非零动量等。这些新现象促使人们重新考虑强场电离中的非偶极效应。对于里德堡原子,电子的分布尺寸很大,非偶极将更加重要,有很多问题需要更加精确的理论模型去研究。例如,在强激光场驱动下,多光子共振激发及受挫隧穿电离中的非偶极效用、里德堡态原子光电离的非偶极效应、里德堡态之间的非偶极跃迁等,都有待研究。
