基于变截面铺层的无人机机翼结构-材料一体化轻量化设计

杨益彰 廖耀青

摘要：为减轻无人机机翼结构的质量，从而提升无人机性能和飞行效率，文章考虑应用变截面铺层优化设计方法从结构尺寸和铺层设计两方面对机翼结构进行结构-材料一体化优化设计。首先，对某三梁多肋式机翼结构进行了仿真分析，确定了优化方向。其次，结合优化区域，采用变截面铺层优化方案，确定了变截面尺寸结构和变截面最优铺层方案。最后，对优化前后的机翼结构仿真结果对比分析，发现机翼质量降低了30.43%，最大应力降低了27.61%、失效指数降低了54.72%，翼尖最大变形量增大了15.48%，且远满足设计要求。

关键词：复合材料；无人机；机翼；轻量化；遗传算法

中图分类号：V279  文献标志码：A

0 引言

随着无人机产业的快速发展，提高无人机性能和飞行效率的需求是无人机制造商持续关注的问题。机翼作为无人机主承力结构，承担了无人机大约70%的气动载荷，是主要的升力部件，其结构性能对整个无人机的飞行性能起着决定性的作用［1］。因此，保证结构强度的情况下，具有轻量化、高刚度特性的机翼结构是提高无人机各项性能的关键要素。

新型轻质高强材料中，碳纤维复合材料具备结构整体成型等特性，可大幅减少零件和紧固件数量，简化连接和装配，实现材料、功能、结构的一体化设计［2］。刘峰等［3］设计了一款常规气动布局的三机身结构碳纤维复合材料太阳能无人机，并结合铺层优化，机翼有效地减重12.3%。Teng等［4］利用代理模型对某长航时无人机机翼进行多目标多学科优化，与基准翼相比，气动性能提高20%，结构重量减轻43%。Hanif等［5］采用试验设计（DOE）和响应面法（RSM）技术对某型飞机机翼进行了优化设计，结果表明该优化技术可以有效地降低结构的应力和整体重量。因此，碳纤维复合材料应用于无人机机翼并结合结构设计，实现轻量化的同时对无人机长航时、气动性能及高机动性等的改善具有重大研究意义。

无人机机翼结构-材料一体化设计是一个多参数、多响应的复杂系统优化问题。仅凭借工程师利用仿真技术和工程经验从参数组合中盲目地挑选满意的方案需耗费大量计算资源和时间［6-8］。针对上述问题，国内外学者做了大量研究。Liu等［9］采用全局翼与局部面板的集成优化策略，优化后机翼的结构重量减少了40%。Abdelkader等［10］开发了一个用于飞机机翼高保真多学科优化设计的全自动化框架，结合参数化建模和基于代理模型的优化策略对某高速客机机翼进行优化设计。结果表明，在保持升力系数和结构安全的前提下，飞机航程增大了8.9%。

本文提出一种变截面铺层优化设计方案，从结构尺寸和铺层设计两方面对机翼结构进行结构-材料一体化优化设计。文章首先分析机翼结构受力情况，进而开展变截面铺层优化，进一步提升机翼结构性能。

1 有限元建模及仿真分析

1.1 模型网格化

本文选用某三梁多肋式机翼结构作为研究对象，其机翼结构主要包括有蒙皮、翼梁和翼肋。不影响仿真结果的前提下，对模型进行几点简化。机翼的有限元模型，如图1所示。

（1）将蒙皮、翼肋、梁等结构均视为薄壁结构，全部采用四节点和三节点壳单元进行网格划分，网格大小为3×3 mm。

（2）忽视铆钉、桁条等来连接，机翼各结构之间采用RBE2连接，将机翼结构视为一个整体。

1.2 材料与铺层

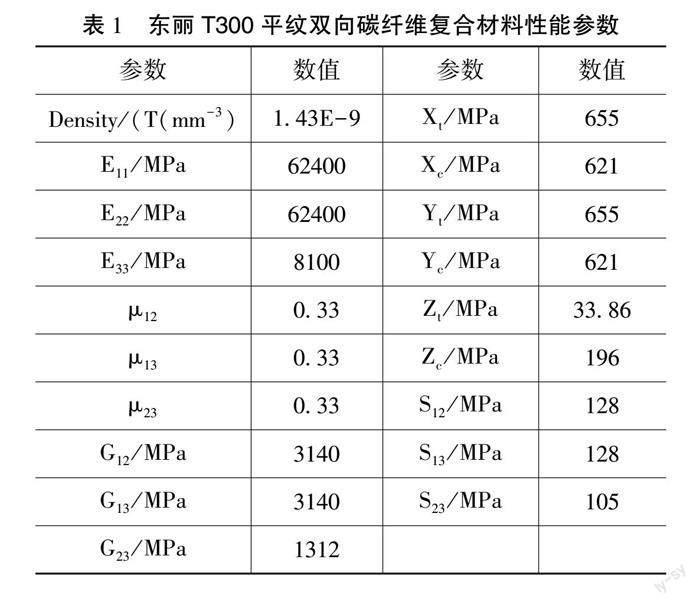
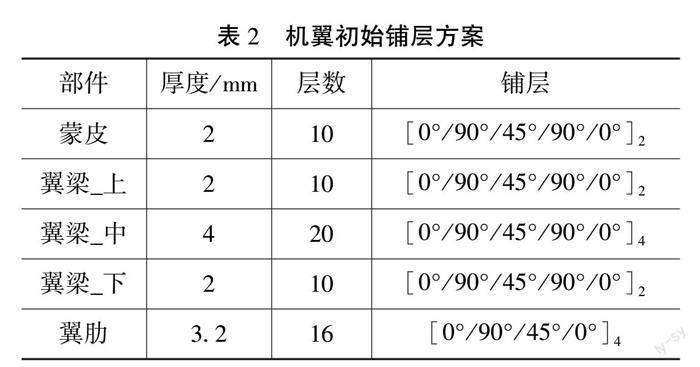
机翼所有部件均采用东丽T300平纹双向碳纤维复合材料［3］，其材料力学性能参数如表1所示。各部件的结构属性及初始铺层方案如表2所示。

1.3 载荷与边界条件

无人机起飞结构质量为7 kg，无人机安全系数取f=2，由机翼升力公式可得单侧机翼需提供210 N的升力。采用Profili软件分析机翼在雷诺数为181000、迎角为6°情况下的外载荷分布［11-12］，如图2所示。

假设机翼与机身处链接为锁死状态，将机翼与机身的螺栓连接件省略，对翼根处翼梁结构进行全约束固定代替，即认为机翼结构为一端固定，另一端自由的悬臂梁。

1.4 仿真分析

基于上述构建的无人机机翼有限元模型，对整个机翼结构进行静强度分析，其应力云图，如图3所示。由图3应力云图分析可知，最大应力位于翼根的前翼梁和中翼梁附近，为432.1 MPa，机翼其他部分的受力均很小，说明机翼结构布局不合理，导致材料利用率较低。因此，可以加強翼根处的结构强度，削减受力小的部分结构的尺寸厚度，力求满足机翼结构处于刚度、强度设计要求的前提下，使得机翼质量最小化。

2 研究方案

2.1 设计变量

由于机翼结构受力最严重的地方集中在翼根的翼梁处，因此可以在结构优化的基础上对翼梁进行变截面厚度过渡区铺层处理（见图4）。根据复合材料的铺层特性，各截面厚度的变化值为单层厚度的整数倍，各区域具体铺层层数，如表3所示。结合翼梁结构的铺层层数，设定各阶梯的铺层顺序，其备选方案如表4所示。

2.2 优化模型

变截面铺层优化以不同翼梁结构的变截面阶梯对应的铺层顺序为设计变量，以机翼总质量（M）和最大位移量（L）最小化为优化目标，优化部件最大应力（F）和失效指数（H）作为约束。由于优化数据均由有限元模型通过仿真分析获得，而构建有限元模型时进行了部分简化，故对两个约束值赋予0.8的安全系数［13-14］。其优化模型如式（1）所示：

MinimizeM（x，y，z），L（x，y，z）

S.t.F（x，y，z）≤524

H（x，y，z）≤0.8

x∈［101，102，103，104］

y∈［201，202，203］

z∈［301，302，303］（1）

式（1）中：M（x，y，z）表示机翼的总质量；F（x，y，z）表示机翼的最大应力指数；H（x，y，z）表示机翼各部件的最大失效；L（x，y，z）表示机翼结构的最大位移量；x，y，z分别为三个阶梯对应的铺层方案。

2.3 优化结果

针对上述优化问题，基于Isight优化平台，构建响应面近似模型，并采用NSGA-Ⅱ算法［15］进行寻优，对应的优化算法参数设置，如表 5所示。机翼总质量和最大位移量的权重根据分别赋值为 0.6 和 0.4。最终获得的翼梁结构最优变截面铺层方案和指标值，如表6所示。

2.4 对比验证

由于基于近似模型通过NSGA-Ⅱ算法获取的最优解结果有一定的偏差，因此为验证优化结果，本文将表6中的铺层数据代入到有限元模型，其仿真结果，如图5所示。优化前后的碳纤维复合材料机翼结构安全性能及轻量化情况，如表7所示。

由表7中多级优化前后的数据分析对比可知，一方面，有限元模型与近似模型仿真误差最大为8.2%，可见近似模型在机翼静力分析方面有较高的精度保证。另一方面，经过变截面铺层优化后，机翼结构质量得到大幅度的降低，高达30.43%，且其最大应力、失效指数和最大变形量均得到较大幅度的改善。综上分析可知，经过优化后，机翼的应力分布更均匀，材料的利用率得到较大的提升，且各性能指标均满足要求。

3 结语

本文根据机翼结构轻量化的项目需求，从结构尺寸和铺层顺序两方面着手，开展针对全复合材料机翼结构的变截面铺层优化设计研究，主要结论如下所示：

（1）通过仿真分析，发现机翼结构的主要受力点集中在翼根区域的翼梁结构上；机翼初始结构满足性能要求，但具有较大的优化空间。

（2）结合优化区域，采用多级优化方案，确定了尺寸结构和变截面最优铺层方案；对优化前后的机翼结构仿真结果对比分析，发现机翼质量降低了30.43%，最大应力降低了27.61%、失效指数降低了54.72%，翼尖最大变形量增大了15.48%，且远满足设计要求。

参考文献

［1］丁玲.全复合材料无人机机翼结构优化设计［D］.长春：中国科学院研究生院（长春光学精密机械与物理研究所），2014.

［2］周何，李小兵，张婷，等.航空发动机复合材料风扇叶片制造工艺应用进展［J］.航空制造技术，2022（13）：84-91.

［3］刘峰，闫清云，王卓煜.全复合材料太阳能无人机结构设计与分析［J］.复合材料科学与工程，2022（4）：32-39.

［4］TENG L，LI L，ZHOU S，et al. Multi-Objective Multidisciplinary Optimization of Long-Endurance UAV Wing Using Surrogate Model in ModelCenter［C］. 15th AIAA/ISSMO Multidisciplinary Analysis & Optimization Conference，2013.

［5］HANIF A，LI H S，RAZA M A，et al. Optimization Design of an Aircraft Wing Structure based on Response Surface Method［J］. IOP Conference Series：Materials Science and Engineering，2020（1）：12024.

［6］PROENCA T，AFONSO F，LAU F，et al. On the design and manufacturing of topologically optimized wings［J］. Rapid Prototyping Journal，2022（4）：28.

［7］CONLAN-SMITH C，ANDREASEN C S. Aeroelastic Optimization of Aircraft Wings Using a Coupled Three-Dimensional Panel-Beam Model［J］. AIAA Journal，2021（6）：1-14.

［8］王守川，郝巨，李西宁，等.飞机机翼模块化装配技术研究［J］.航空制造技术，2018（13）：68-73.

［9］QIANG L，JRAD M，MULANI S B，et al. Integrated Global Wing and Local Panel Optimization of Aircraft Wing［C］.56th AIAA/ASCE/AHS/ASC Structures，Structural Dynamics and Materials Conference，2015.

［10］BENAOUALI A，KACHEL S.Multidisciplinary design optimization of aircraft wing using commercial software integration［J］. Aerospace science and technology，2019（9）：766-776.

［11］李珂.長航时无人机机翼平面参数及翼型选择分析［J］.飞行力学，2007（3）：9－11，16.

［12］张庆余，何景武.大展弦比复合材料机翼结构后屈曲分析［J］.飞机设计，2008（1）：28－32.

［13］廖耀青.碳纤维复合材料汽车座椅靠背骨架结构设计与仿真［D］.温州：温州大学，2021.

［14］XIONG F，WANG D，MA Z. et al. Structure-material integrated multi-objective lightweight design of the front end structure of automobile body［J］. Struct Multidisc Optim，2018 （57）：829-847.

［15］張文晴，侯精明，王俊珲，等.耦合NSGA-Ⅱ算法与高精度水动力模型的LID设施优化设计方法研究［J］.水资源与水工程学报，2022（4）：133-142.

（编辑 姚 鑫）

Structure-material integrated lightweight design of UAV wing based on variable cross-section ply

Yang  Yizhang， Liao  Yaoqing

（Zhejiang College of Security Technology， Wenzhou 325016， China）

Abstract：  In order to reduce the weight of the wing structure of the UAV and improved the performance and flight efficiency of the UAV， the variable cross-section ply optimization design method was used to optimize the structure-material integration design of the wing structure from two aspects of structural size and ply design. Firstly， the simulation analysis of a three-beam multi-ribbed wing structure was carried out， and the optimization direction is determined. Then， combined with the optimization area， the variable cross-section ply optimization scheme was adopted to determine the variable cross-section size structure and the optimal ply scheme. Finally， the simulation results of the wing structure before and after optimization were compared and analyzed. It was found that the wing mass was reduced by 30.43 %， the maximum stress was reduced by 27.61 %， the failure index was reduced by 54.72 %， and the maximum deformation of the wing tip was increased by 15.48 %， which far meets the design requirements.

Key words： composite; UAV; wing; lightweight; genetic algorithm