基础隔震耗能结构基于Kanai-Tajimi谱的随机响应简明解法研究
2023-08-18邹万杰覃永安李创第经承贵
邹万杰,覃永安,李创第,经承贵,韩 红
(广西科技大学 土木建筑工程学院,广西 柳州 545006)
0 引言
长期以来,地震灾害给人类的生活带来了严重的困扰,不仅影响着人们的正常工作,还威胁着人类的生命安全。地震曾经造成的核泄漏、交通枢纽破坏和房屋损坏等重大安全事故,引发了巨大的财产损失与人员伤亡[1-3]。近年来,我国自然灾害频发,地震造成的灾害尤为明显,如5.12汶川地震和青海门源6.9级地震等[4-5],因此,众多学者一直致力于地震对结构影响的研究。为了研究地震动对结构的影响,国内外众多学者提出了许多随机地震动模型。HOUSNER[6]在1947年首次提出白噪声模型,认为地震动功率并不随着频率的变化而改变,即功率谱密度图像为一条水平的直线,大大简化了对结构的动力响应分析,促进了人们对地震动模型的研究;此后,日本学者KANAI[7]和TAJIMI[8]认为白噪声过程能量在频域内的均匀分布并不符合实际情况,因此提出了一种过滤的白噪声模型,即Kanai-Tajimi模型,该模型考虑了场地频率和阻尼比对频域能量分布的影响,弥补了白噪声模型未能考虑场地动力特征对于地震动影响的缺陷,更符合工程实际应用,对于理论研究有着深远的意义,该模型在地震工程界至今仍被广泛使用。
为了减缓地震对建筑物造成的影响,一味地依靠增加结构的刚度并不能取得良好的效果,因此工程技术人员常在结构中加入合适的阻尼器来耗散地震输入的能量,如调谐质量阻尼器、调频液体阻尼器和粘弹性阻尼器等[9-11]。而作为耗能减振装置的粘弹性阻尼器由于其减振效果好和造价低廉等特点,且其相较于其他类型阻尼器而言,安装方便且需要的空间较小,故受到广大工程技术人员与研究者的重视,应用越来越广泛。为了方便研究,国内外学者对于粘弹性阻尼器提出了各种力学模型,如Maxwell模型、Kelvin模型、广义Maxwell模型和分数导数模型等[12-15]等。其中:广义Maxwell模型能够通过调整参数更好地描述该类型阻尼器的粘弹性行为,有更广的适用范围[16]。
基础隔震结构自被提出以来就受到了广大工程技术人员的青睐,其主要原理是在上部结构与基础间加入隔震装置,削弱地震向上部结构传递能量,其中橡胶隔震支座被广泛应用[17]。实践证明:与抗震结构相比基础隔震结构表现出其独特的优越性[18],在数次大地震中上部结构都得到了很好的保护,如美国北岭地震和中国台湾海峡地震[19-20],美国北岭地震中有记录表明:采用了隔震技术的南加州医院顶层加速度峰值仅为基础的一半,院内设备设施得到了良好的保护。因此,众多的国内外学者对抗震、隔震结构进行了深入的研究,并且取得了极大的进展,促进了各国建筑设计规范的完善[21-23]。然而,地震动属于随机激励,因此基于随机振动理论分析基础隔震结构的响应仍有重要的研究价值[24-25]。
针对使用传统方法分析隔震耗能结构在随机地震激励下计算复杂和耗时较长等问题,本文提出了一种简明解法。联立广义Maxwell阻尼器本构方程与原结构运动方程,重构结构运动方程,再利用复模态法将重构所得的结构运动方程解耦,获得响应的统一表达式。其次计算激励功率谱与响应功率谱的二次正交式;最后根据随机振动理论获得了结构响应0~2阶谱矩及方差。该求解过程为解析求解且无假设和近似,解的形式相较于传统形式更加简洁,为隔震耗能结构在随机地震动激励下的响应分析在工程中的应用打下良好基础。
1 耗能结构的地震动方程
1.1 结构运动方程
设n层结构的质量、阻尼和刚度的矩阵分别为M、C和K,各层均设置广义Maxwell阻尼器,上部结构的阻尼力及其位置矩阵分别为PQ(t)和Tp,结构计算简图如图1所示。
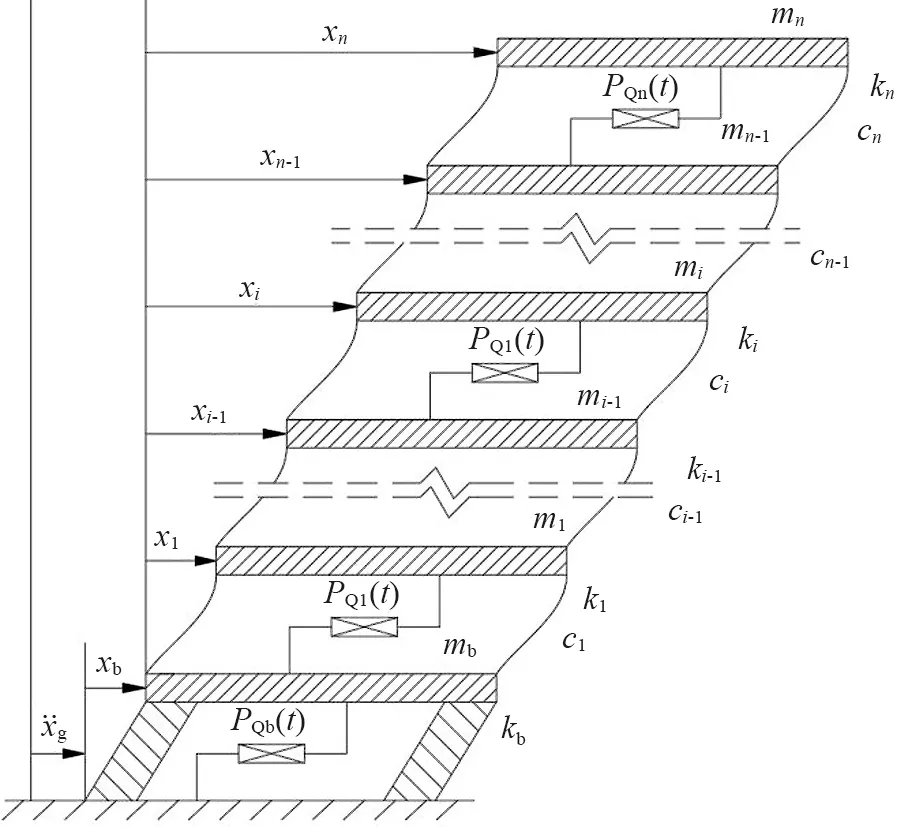
图1 结构计算简图Fig. 1 Calculation diagram of the structure
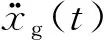
(1)
(2)
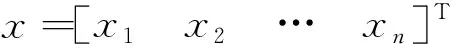

(3)
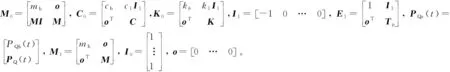
1.2 广义Maxwell阻尼器本构关系
广义Maxwell模型阻尼器是由一个线性弹簧和一系列的Maxwell模型单元并联而成,广义Maxwell模型阻尼器计算简图如图2所示,Maxwell模型阻尼器计算简图如图3所示。
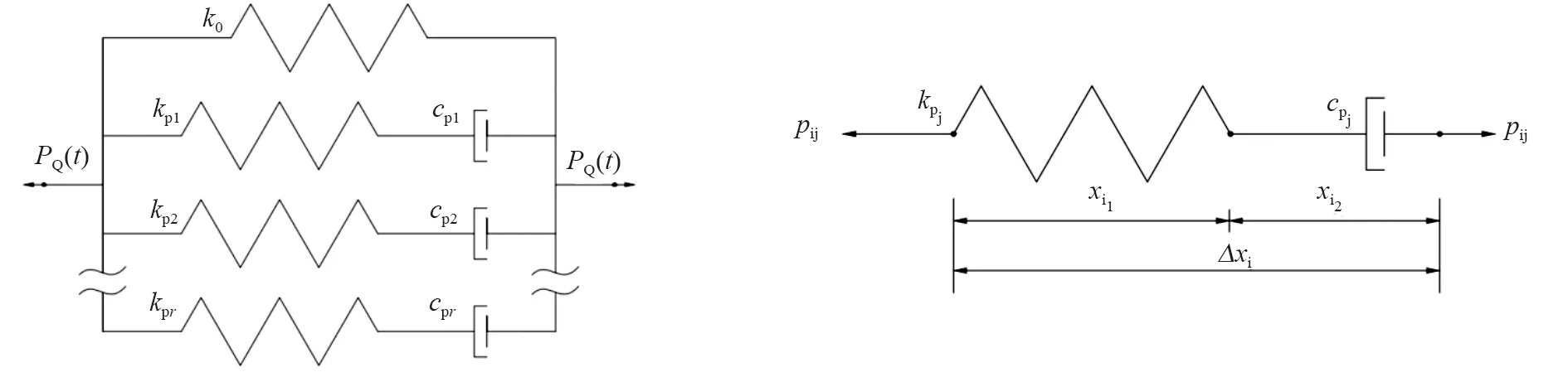
图2 广义Maxwell阻尼器计算简图 图3 Maxwell阻尼器计算简图
广义Maxwell阻尼器本构关系为:
(4)
式中:PQb(t)和PQi(t)分别为隔震层和第i层阻尼器的总阻尼力,k0为阻尼器平衡刚度,pbj和pij为每个Maxwell单元的阻尼力。其中:i=1~n,n为楼层数目,j=1~r,r为广义Maxwell阻尼器中标准Maxwell阻尼器单元的个数。
将式(4)写成矩阵形式,有:
(5)

将式(5)简写为:
PQZ(t)=K1x0+D1P
(6)
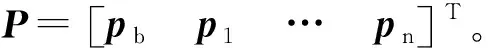
各分支Maxwell阻尼器的微分关系为:
(7)
式中:kPj和cPj分别为第j个标准Maxwell阻尼器单元的刚度和阻尼。
将式(7)写成矩阵形式,有:
(8)
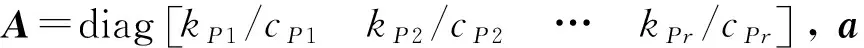
将式(8)简写为:
(9)
1.3 重构结构运动方程
联立式(3)和式(6),重构结构的运动方程:
(10)
引入状态变量:
(11)
联立式(9)和式(10)写成状态方程:
(12)
其中:
式中:o1为元素均为0的(n+1)×(n+1)阶矩阵;o2为元素均为0的(n+1)×(rn+r)阶矩阵,o3为元素均为0的(n+1)×1阶向量;o4为元素均为0的(rn+r)×1阶向量;E2为n+1阶单位矩阵;E3为rn+r阶单位矩阵;N为状态方程中矩阵M2和K2的阶数,N=rn+r+2n+2。
2 结构响应统一表达式
由于式(12)为非经典系统,故引入复模态变换进行计算。存在左和右特征向量V,U使M2和K2对角化,特征值矩阵q满足关系如下:
(13)
引入复模态变换:
y=Uz
(14)
式中:z为广义复模态向量。
联立式(12)、式(13)和式(14),化为复模态响应方程:
(15)
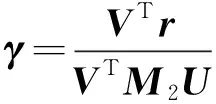
将式(15)写成分量形式:
(16)
式中:zk、qk和γk分别为z、q和γ的分量。
根据虚拟激励法[26],式(16)的频域解为:
(17)
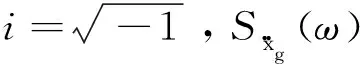
结合复模态法和虚拟激励法,联立式(11)、式(14)和式(17),求得基础耗能隔震系统响应的频域解如下。

(18)
(19)
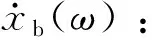
(20)
(21)
第i层的层间位移频域解Δxi(ω):
(22)
(23)
由式(4),隔震层阻尼力频域解PQb(ω)为:
(24)
比较系统各响应式(18)~式(24),均为zk(ω)的函数,故在频域内将系统响应写为统一表达式:
(25)
式中:Γk为第k个广义模态变量zk(ω)的模态参与系数。
3 二次正交化求解
3.1 频率响应函数的二次正交化
根据虚拟激励法和式(25),系统各响应X(ω)的功率谱可表示为:
(26)
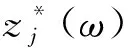
联立式(17)和式(26)得:
(27)
(28)
式中:ηk=Γkγk,ηj=Γjγj。
由频率响应函数式(28)的对称性,重写为:
(29)
将频响函数式(29)最终简写为:
(30)
3.2 Kanai-Tajimi谱的二次正交化
本文采用Kanai-Tajimi谱随机地震动模型,该模型功率谱传统表达式如下:
(31)
式中:ωg和ξg分别代表场地土的卓越频率和阻尼比,S0为地震动强度常数。
鉴于Kanai-Tajimi谱的传统表达式复杂且难以通过积分运算获得结构响应,故使用留数定理,得到Kanai-Tajimi谱的二次正交式如下:
(32)
3.3 响应功率谱的二次正交化
将式(30)和式(32)代入式(27),得到系统响应功率谱:
(33)
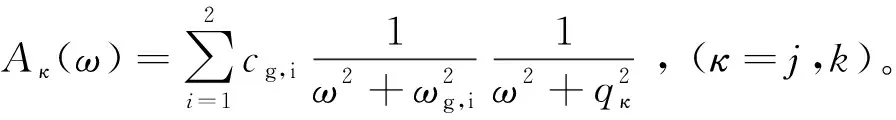
由于频响函数和Kanai-Tajimi谱都是二次正交的形式,因此,响应功率谱也是二次正交的形式。
4 响应谱矩和方差
根据随机振动理论[27],系统响应的i阶谱矩定义为:

(34)
将式(33)代入式(34),得系统响应谱矩:
(35)


(36)
(37)
将式(36)代入式(35),可得系统响应0阶谱矩:
(38)
将式(37)代入式(35),可得系统响应1阶谱矩:
(39)
根据随机振动理论,系统响应变化率的0阶谱矩等于响应的2阶谱矩,即:
(40)
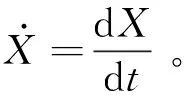
系统响应位移的方差等于其0阶谱矩,系统响应速度的方差等于其2阶谱矩,即:
(41)
(42)
5 算例
某中学教学楼,地上5层,每层楼高度皆为3.6 m,即h1~h5=3.6 m,教学楼总高18 m。隔震支座设置于基础底部,为橡胶隔震支座。地震烈度为7度,Ⅱ类场地。上部结构为全现浇钢筋混凝土框架结构,每层质量为m1~m5=300×103kg,抗侧刚度为k1~k5=150×106N/m,结构阻尼比ξ=0.05。隔震层质量mb=350×103kg,隔震层刚度为kb=55×106N/m,隔震层阻尼比ξb=0.1。隔震层与上部结构每层均设置相同的广义Maxwell阻尼器,其参数为:分支一标准Maxwell阻尼单元的刚度kP1=4.05×105N/m,松弛时间t1=0.10 s;分支二标准Maxwell阻尼单元的刚度kP2=3.78×105N/m,松弛时间t2=0.12 s;阻尼器平衡刚度k0=3.6×105N/m。根据文献[28],Kanai-Tajimi功率谱参数为:场地卓越频率ωg=15.71 rad/s,场地阻尼比ξg=0.72,功率谱强度因子S0=31.76×10-4m2/s3。
5.1 功率谱二次正交式验证
图4(a)~(d)分别绘制了地面加速度功率谱、隔震层绝对位移功率谱、隔震层绝对速度功率谱和隔震层阻尼力功率谱。可以看出:二次正交化Kanai-Tajimi功率谱、响应功率谱与传统Kanai-Tajimi功率谱、虚拟激励法(公式推导见附录A)计算的功率谱均重合,验证了本文研究的简明解法的正确性。
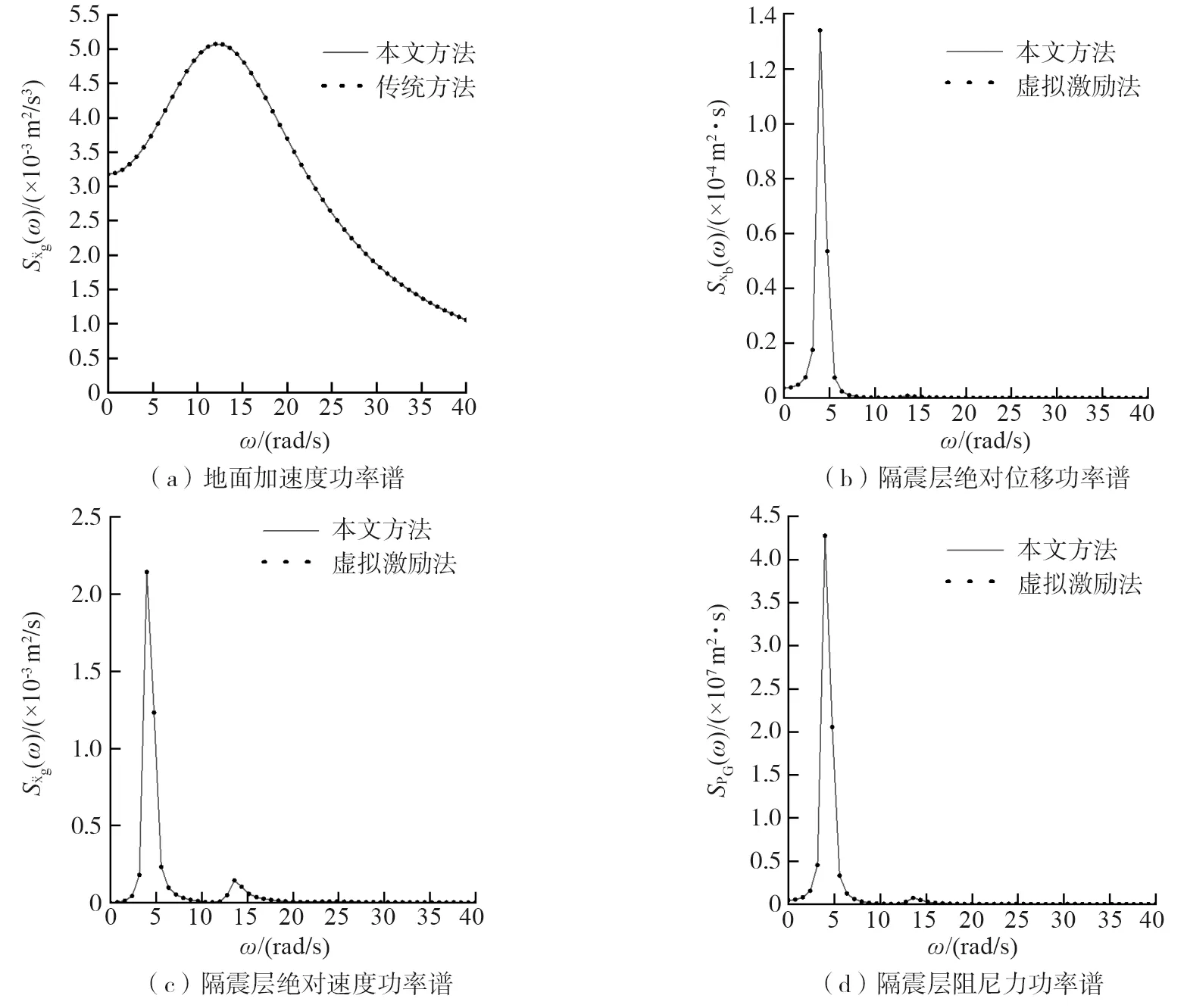
图4 功率谱对比图Fig. 4 Power spectrum comparison chart
5.2 谱矩计算精度和效率
图5(a)~ (f)分别绘制了结构位移0~2阶谱矩和层间位移0~2阶谱矩。虚拟激励法积分区间均为[0,600],取积分步长分别为1.00 rad/s、0.50 rad/s和0.01 rad/s与本文计算结果对比,由图像可知:响应谱矩应用虚拟激励法计算时,随着积分步长的减小,所得图像逐渐与本文简明解法的图像重合,验证了本文方法计算谱矩的正确性。

图5 谱矩对比图Fig. 5 Spectrum moment comparison chart
由于虚拟激励法计算谱矩时采用数值积分,因此其计算精度与积分步长和积分区间的选择有密切关系。表1为本文方法与虚拟激励法计算的隔震层位移0~2阶谱矩计算精度与计算效率,其中积分步长取为0.001 rad/s,可以看出:虚拟激励法随着积分区间的逐渐增大,计算得到的谱矩与本文二次正交化法所得结果误差值减小,验证了本文方法的正确性,且本文方法计算0~2阶谱矩耗时更短。
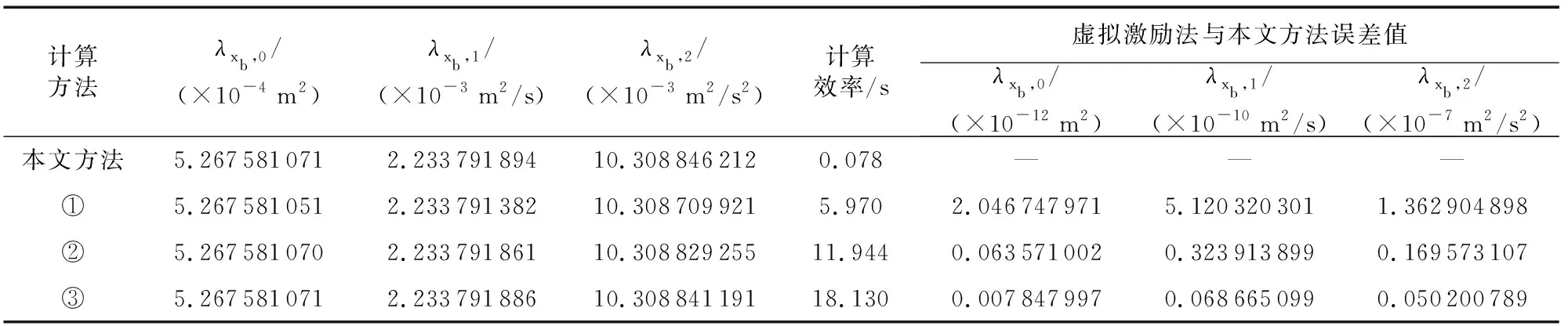
表1 隔震层位移0~2阶谱矩计算精度和效率Table 1 Calculation accuracy and efficiency of 0~2 order spectral moment of isolation layer displacement
6 结论
本文针对基础隔震结构设置广义Maxwell阻尼器基于Kanai-Tajimi谱下的地震动响应进行了研究,结论如下:
1)本文利用复模态法、二次正交化法成功获得了结构响应谱矩及方差的简明表达式,该表达式因无需进行数值积分运算故具有更高的计算效率。
2)在最后的算例中,当虚拟激励法积分步长取值足够大、积分间距取值足够小,各响应功率谱图像与虚拟激励法所算结果均吻合,验证了本文的正确性,且本文方法具有更好的计算精度。
3)由于其他平稳随机地震谱均是在Kanai-Tajimi谱基础上的延伸,故本文方法可以推广至结构在各类平稳随机地震谱下随机响应解法的研究,具有良好的实用性。
附录A:广义Maxwell阻尼器耗能结构的虚拟激励法
根据虚拟激励法,文中的式(3)可表示为:
(a)
在式(a)中,需要求的未知数为x0(ω)和PQz(ω)。
将文中的式(9)用频域形式表示:
iωP(ω)+αP(ω)=Biωx0(ω)
(b)
将文中的式(6)用频域形式表示:
PQZ(ω)=K1x0(ω)+D1P(ω)
(c)
将式(b)代入式(c)可得:
(d)
联立式(a)和(d)可得x0(ω)的频域解:
(e)
上部结构第i层的层间位移频域解Δxi(ω)为:
Δx1(ω)=x1(ω)i=1
(f)
Δxi(ω)=xi(ω)-xi-1(ω)i=2~n
(g)
将频域解x0(ω)和Δxi(ω)用统一符号X(ω)表示,则系统响应X(ω)的功率谱可表示为:
SX,PEM(ω)=X(ω)X*(ω)
(h)
式中:X*(ω)是X(ω)的共轭项。
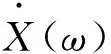
(i)
将式(i)代入式(34),可得系统响应的0~2阶谱矩:

(j)
