海相淤泥水泥土变形特性试验研究*
2023-08-18吕业锋杜建成唐昌意马祖遥
吕业锋, 杜建成, 唐昌意, 马祖遥
(珠海市规划设计研究院,珠海 519000)
0 前言
我国沿海地区普遍分布有深厚软土层,其具有含水量高、压缩性大、灵敏度高、孔隙比大、渗透性差、强度低、欠固结、流变触变等特性,呈流塑状态,工程性质较差,工程问题较突出[1-6]。变形参数是水泥加固土桩复合地基沉降计算的重要参数,国内规范给出了相关经验取值,其中《复合地基技术规范》(GB/T 50783—2012)[7]规定压缩模量Ep可取桩体水泥土强度的100~200倍,桩较短或桩体强度较低者可取低值,桩较长或桩体强度较高者可取高值。《公路软土地基路堤设计与施工技术细则》(JTG/T D31-02—2013)[8]中规定压缩模量Ep=83.4qu(qu为90d水泥土无侧限抗压强度)。《建筑地基处理技术规范》(DBJ 15-38—2019)[9]给出水泥土搅拌桩的压缩模量Ep=(100~120)fcu(fcu为90d水泥土无侧限抗压强度)。《广东省公路软土地基设计与施工技术规定》(GDJTG/T E01—2011)[10]规定压缩模量Ep应根据压缩试验确定,无试验数据时可取Ep=(60~80)ηfcu(η为水泥土桩身强度折减系数)。综上,不同的规范给出截然不同的计算公式,给工程设计取值造成极大的困扰。
国内专家学者针对水泥土的变形特性开展了相关的研究,骆嘉成等[11]采用浅层固化的方法获得固化剂掺量为2%~8%时,浅层固化淤泥形成的硬壳层的承载力特征值为117~200kPa,固化淤泥的变形模量在8.5~14.59MPa。陈晓静等[12]依托工程项目的水泥土配比试验,建立水泥土无侧限抗压强度与黏聚力、变形模量的关系,得出淤泥质土和淤泥水泥土变形模量值小于规范推荐值。张新建等[13]依托珠海市洪湾北片区市政基础设施项目,通过室内试验获得无侧限抗压条件下淤泥水泥土的压缩性随着龄期和水泥掺入量的增加而变小的规律。阮庆等[14]结合湖南省洞庭湖区某高速公路淤泥质黏土软土地基处理工程,进行淤泥质黏土水泥改良土的无侧限抗压强度试验,研究水泥土无侧限抗压强度的影响因素、水泥土的应力、应变关系和变形模量的变化规律以及试样的破坏模式;研究结果表明: 水泥土的变形模量随着水泥土的无侧限抗压强度的增大而增大。侯龙清等[15]等通过室内试验揭示南京地区水泥土的变形特征和强度特性,并得出水泥掺入比和龄期对水泥土变形和强度的影响规律,提出“强度增长的临界龄期”的概念。
《地基处理手册》[16]提供了长江三角州、天津等地区的淤泥质黏土的相关试验成果。软土的工程性质与成因、应力历史等有关,具有明显的区域性特征,不同的水泥加固软土呈现不同的变形特征,目前针对广东省珠海地区淤泥水泥土特性的研究成果较少,正值珠海市地方标准编制《路桥工程软土地基处理技术指南》之际,本文选取珠海地区典型海相淤泥为研究对象,分析海相淤泥水泥土(简称水泥土)在无侧限和有侧限抗压强度试验下的变形特性,获得变形特征参数,研究成果可为珠海地区软土地基处理及《路桥工程软土地基处理技术指南》编制提供参考。
1 海相淤泥工程特性
现场取典型淤泥样品,通过室内土工试验测试了淤泥的物理力学性质指标、渗透系数和颗粒组成,详见表1和表2。由表1、2可知:淤泥具有含水量高、孔隙比大、黏粒含量高、呈流塑状态等特性,属于高液限土。由表2可知,淤泥的颗粒主要由粉粒、黏粒和胶粒组成,其中粉粒含量57.2%,黏粒和胶粒含量42.8%,说明淤泥细颗粒含量较高。

表1 淤泥的物理力学性质指标

表2 淤泥的颗粒组成
2 试验方案
试验执行标准为《水泥土配合比设计规程》(JGJ/T 233—2011)。试验内容为无侧限抗压强度试验和压缩试验。水泥掺入量为15%、20%和25%,水灰比为0.6。
无侧限抗压强度试验:试件尺寸为70.7mm×70.7mm×70.7mm立方体,养护龄期为7、14、28、60、90、120d,每个龄期每种水泥掺入量均为6个试件,共计108个试件。试验仪器为电液伺服万能试验机。无侧限抗压强度试验现场及部分试件照片见图1。

图1 无侧限抗压强度试验现场及部分试件照片
有侧限压缩试验:试件为内径61.8mm、高度20mm的圆柱体,养护龄期为7、14、28、60、90d,每个龄期每种水泥掺入量均为3个试件,共计45个试件。试验仪器为三联式固结仪。有侧限压缩试验现场及部分试件照片见图2。

图2 有侧限压缩试验现场及部分试件照片
3 无侧限抗压强度试验水泥土变形特征
3.1 应力-应变曲线分析
典型的无侧限抗压强度试验得到的水泥土(水泥掺入量15%,龄期28d)应力-应变曲线如图3所示,由图3可知:应力-应变曲线大致可分为三段,第Ⅰ阶段,在较小的应力水平下,随应力的增大,应变快速增长,曲线斜率较小,表现出压密蠕变的变形特征;第Ⅱ阶段,应变随着应力的增加而快速增长,曲线基本呈直线,斜率较大,表现出弹性变形特征;第Ⅲ阶段,应力增长到最大值后维持不变,应变快速增加;之后应力缓慢较小、应变继续增大,表现出塑性变形特征。由此可知,水泥土在无侧限压缩状态下呈现出弹塑性变形特征。
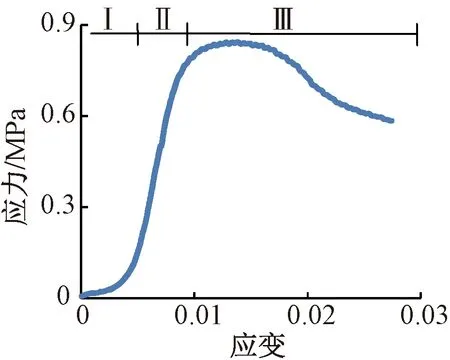
图3 水泥土应力-应变曲线
3.2 弹性模量与无侧限抗压强度的相关性分析
弹性模量是基坑工程重力式水泥土墙变形计算的重要参数。由3.1节可知,图3的应力-应变曲线中第Ⅱ段即为弹性变形阶段,该段曲线的斜率即为水泥土的弹性模量,由此计算得到不同龄期不同水泥掺入量的水泥土弹性模量见表3。

表3 不同水泥掺入量不同龄期水泥土弹性模量/MPa
绘制水泥土弹性模量随龄期的关系曲线见图4。由图4可知,弹性模量随着龄期的增大逐渐增大,随着水泥掺入量的增加而增大。采用回归分析方法得到弹性模量与龄期的换算公式,如式(1)~(3)所示,由换算公式可知,弹性模量与龄期呈线性相关性,拟合优度R2=0.932~0.982,表明拟合程度较好。

图4 弹性模量与龄期关系曲线
E15%= 1.020d+ 143.6,R2= 0.982
(1)
E20%= 0.989d+ 224.2,R2= 0.955
(2)
E25%= 0.823d+ 305.9,R2= 0.932
(3)
式中:E15%、E20%、E20%分别为水泥掺入量为15%、20%和25%的水泥土弹性模量;d为水泥土养护龄期。
绘制弹性模量E与无侧限抗压强度fcu的关系曲线如图5所示,由图5可知,弹性模量E随着无侧限抗压强度fcu的增大而增大。采用回归分析方法得到弹性模量E与无侧限抗压强度fcu的换算公式见图5。可知,弹性模量E与无侧限抗压强度fcu呈线性相关性,拟合优度R2=0.931~0.948,表明拟合程度较好。

图5 弹性模量E与无侧限抗压强度fcu关系曲线
采用数理统计的方法得到弹性模量E与无侧限抗压强度fcu的换算系数如表4所示。由表4可知,弹性模量与无侧限抗压强度之比(简称换算系数)最小值155,最大值192,平均值168,标准值170。考虑水泥土复合材料的离散性及基坑变形安全性,可取弹性模量与无侧限抗压强度的换算系数为120~150。
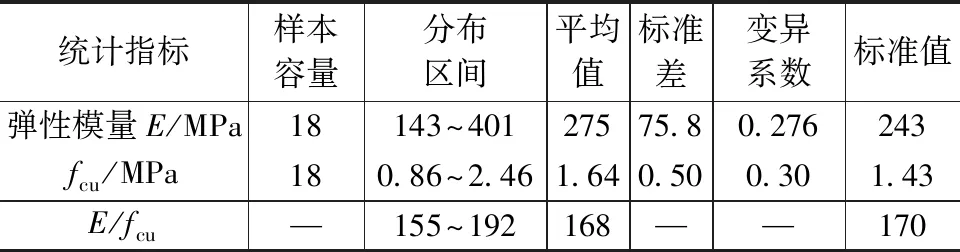
表4 弹性模量与无侧限抗压强度统计分析
珠海某淤泥质土基坑深度4.5m,采用重力式水泥土墙支护方案,设计墙身厚度4.2m,嵌固深度8.5m,坑底裙边采用水泥搅拌桩加固。设计28d无侧限抗压强度0.6MPa,基坑侧向变形计算时取水泥土的弹性模量为(120~150)×0.6=72~90MPa,计算坑顶水平位移为55.1~61.6mm,施工过程监测的水平位移为52~68mm,计算值和监测值较为吻合,说明弹性模量取值是合理的。
4 有侧限压缩试验水泥土变形特征
现场取淤泥原状土样做有侧限压缩试验,获得淤泥孔隙比-压力(e-P)曲线如图6所示。由图6可知,淤泥的初始孔隙比为1.832;淤泥的孔隙比随着压力的增加而减小,压力在0~400kPa时,孔隙比-压力曲线斜率较大,孔隙比减小的幅度较大,曲线呈下降趋势,主要是因为淤泥为饱和软黏土,在压力较小阶段,孔隙中的水因压缩而排出,淤泥体积压缩,孔隙比变小。压力在400~800kPa时,曲线下降的趋势变缓且大致呈直线,荷载主要由土骨架承担,淤泥以弹塑性变形为主。
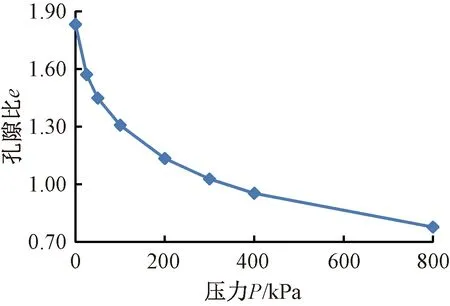
图6 淤泥孔隙比-压力(e-P)曲线
压缩模量是水泥土搅拌桩复合地基沉降计算的重要参数。开展淤泥水泥土试件的有侧限压缩试验,获得不同水泥掺入量不同龄期水泥土的隙比-压力(e-P)曲线,如图7所示。由图7可知,水泥土e-P曲线基本呈直线,水泥土的孔隙比随着压力的增大而减小。对比图6和图7可知,掺入水泥后,初始孔隙比减小不多,但是孔隙比的变化范围明显缩小,说明掺入水泥后土颗粒之间的摩擦力增大,抵抗变形的能力提高;水泥土的e-P曲线相对较平缓,而淤泥的e-P曲线斜率较大,表明,掺入水泥后压缩模量明显增大,压缩性明显变小。当压力为100~200kPa时,水泥土的压缩模量分别为22.0MPa(水泥掺入量15%)、29.2MPa(水泥掺入量20%)、32.1MPa(水泥掺入量25%),淤泥的压缩模量为1.33MPa,水泥掺入量15%、20%、25%的水泥土压缩模量分别为淤泥压缩模量的16.5倍、22.0倍和24.1倍。
根据水泥土e-P曲线,取压力为100~200kPa区段曲线计算压缩模量Es,1-2,取压力为200~400kPa区段曲线计算压缩模量Es,2-4,统计分析结果如表5所示。由表5可知,Es,2-4/Es,1-2=1.5~1.9,均值1.7,说明水泥土的压缩模量随着压力增大而明显增大,因此水泥土桩沉降计算时应根据不同的压力段选取相应压缩模量。
5 压缩模量与弹性模量相关性分析
为了得到弹性模量与压缩模量的换算系数,将弹性模量与压缩模量统计结果列于表6和表7。由表6可知,E/Es,1-2=7.7~12.4,均值9.46;由表7可知,E/Es,2-4=4.5~7.0,均值5.55,因此在换算时可取E/Es,1-2=9.5,E/Es,2-4=5.5。出现弹性模量大于压缩模量的主要原因为:1)压缩模量计算时应力取值范围小于弹性模量计算时的应力取值范围;2)压缩模量计算时包括了孔隙压缩和弹塑性变形的变形量,弹性模量计算时只包括弹性阶段的弹性变形量。
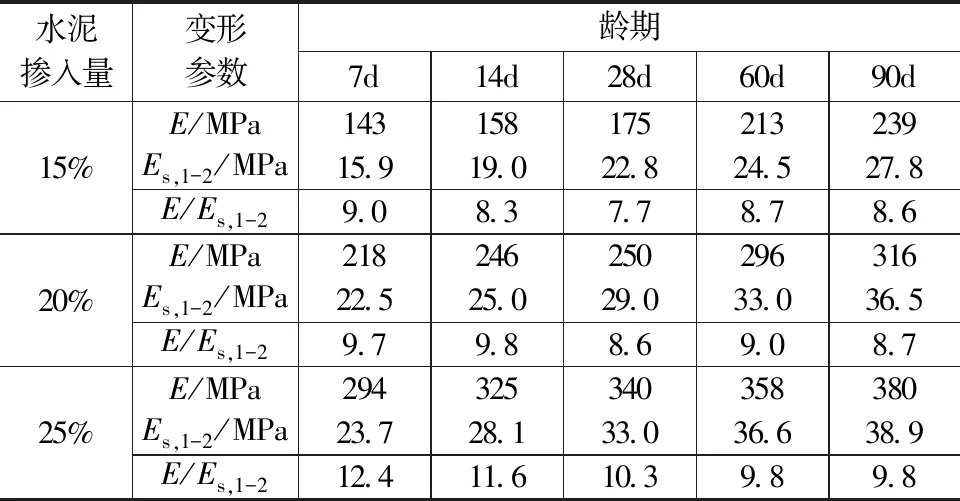
表6 弹性模量E与压缩模量Es,1-2统计结果
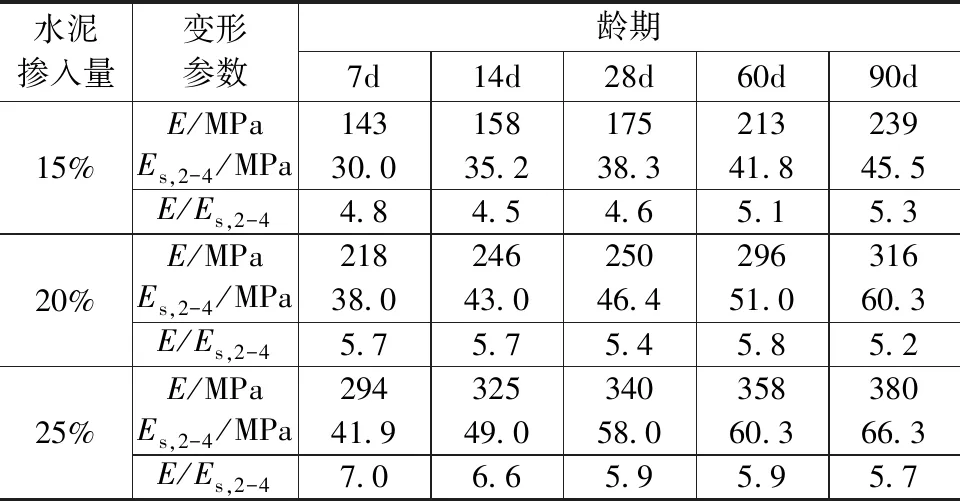
表7 弹性模量E与压缩模量Es,2-4统计结果/MPa
采用回归分析方法得到的弹性模量与压缩模量的拟合曲线如图8和图9所示。由图8和图9可知,弹性模量与压缩模量呈线性相关性,压缩模量随着弹性模量的增大而增大,拟合优度R2=0.927~0.974,表明拟合程度较好。

图8 弹性模量E与压缩模量Es,1-2的拟合曲线

图9 弹性模量E与压缩模量Es,2-4的拟合曲线
6 结论
本文针对不同水泥掺入量不同龄期的水泥土试件进行无侧限抗压试验和有侧限压缩试验,主要结论如下。
(1)水泥土在无侧限压缩的状态下,应力-应变曲线可分为三个阶段,第Ⅰ阶段具有压密变形特征,第Ⅱ阶段具有弹性变形特征,第Ⅲ阶段具有塑性变形特征,表明水泥土具有明显的弹塑性变形特征。
(2)弹性模量随龄期增长而增大,弹性模量随无侧限抗压强度增大而增大,均呈线性相关性,弹性模量可取为无侧限抗压强度的120~150倍。
(3)与淤泥的孔隙比-压力曲线相比,水泥土孔隙比-压力曲线更平缓,压缩模量更高,Es,2-4/Es,1-2=1.5~1.9,均值1.7,说明不同压力段压缩模量差异较大,应根据压力值选取相应压力段的压缩模量。
(4)压缩模量随着弹性模量的增大而增大,两者具有很好的线性相关性,换算时可取E/Es,1-2=9.5,E/Es,2-4=5.5。
