砌体墙力学参数的精密测量

2023-08-16罗若帆董孝曜

世界地震工程 2023年3期

王超,郭迅,,刘娟,罗若帆,张俊,董孝曜

(1. 防灾科技学院中国地震局建筑物破坏机理与防御重点实验室,河北三河 065201;2. 中国地震局工程力学研究所地震工程与工程振动重点实验室,黑龙江哈尔滨 150080)

0 引言

砌体结构具有取材方便、构造简单、施工容易、造价低廉和耐久性好等优势,在我国被广泛应用,但脆性突出的特性使砌体结构在地震作用下破坏非常严重[1]。实际震害显示[2-5],砌体结构底层纵向各轴线刚度差异大时易产生内力集中现象(称为“内力凝聚”),刚度大的构件分配到的地震剪力大,变形能力小,在地震作用下因率先达到位移极限而发生脆性破坏(称为“变形饱和”),并触发结构倒塌。这种破坏机制的核心问题在于地震过程中墙体分配的地震剪力是否超越自身的承载能力,而其剪力分配取决于砌体墙初始刚度的比例,因此准确测量砌体墙的初始刚度和抗剪强度是进行砌体结构倒塌机理研究的基础。

近几十年国内外专家学者对砌体结构抗震性能作了大量的试验研究。MARINILLI等[6]对4片构造柱约束砌体墙进行了拟静力试验,结果表明:构造柱的数量和间距影响墙片的抗震性能;赵成文等[7]对3片不同试验参数的蒸压粉煤灰砖墙体进行了拟静力试验,指出试件抗剪承载力实测值与《建筑抗震设计规范》(GB 50011—2010)[24]的抗震抗剪承载力计算值的平均值之比为3.63,说明规范取值较保守;姚新强等[8]对不同砂浆强度、不同构造措施和开洞的12个墙片进行了拟静力试验,试验表明砂浆强度影响最大,构造措施和开洞影响次之;乔崎云等[9]对3片构造柱约束烧结普通砖砌体墙进行了拟静力试验,试验发现竖向压应力及砌筑砂浆强度的提高使得试件各项力学性能均有一定提升。

学者们大多采用竖向均布加载的悬臂式试验装置来研究砌体墙抗震性能[10-12]。悬臂加荷法是一种接近于实际砌体受力情况的方法,能够模拟墙体在竖向承重和水平抗剪的受力状态,试验方法较为简便且装置简单。但悬臂式试验装置在水平力作用下,墙体会产生一定的弯曲力矩,特别是当墙体的高宽比较大时,试验时容易在底部形成受弯水平裂缝,发生弯剪破坏[13],使墙体位移增大,难以准确获得墙体的初始刚度。此外,大量的震害资料表明砌体结构承重墙体的破坏模式几乎是剪切破坏,难以出现底部的弯曲受拉破坏[14],这是因为实际工程结构通常由多片墙体并联而成,抵抗力臂大,不容易发生弯曲破坏。日本建设省建筑研究所设计了固端平移式试验装置,该装置的加载梁可以强制约束墙体转动,实现试件严格按照受剪机制破坏的试验目的。L形钢架相当于在墙体顶部额外施加一个与试件转动方向反向的弯矩,一定程度上减弱墙体的转动变形[15],进而消除整体弯曲的影响。此种装置结构比较合理,使墙体处于剪切变形状态,最接近多层砌体房屋中墙体在地震时的受力状态,但这种装置的结构比较复杂,L形钢架要求刚度大,四联杆铰支要求杆件尺寸较大,构造精密,不然就不能保证L形钢架横梁在试验中的水平移动[16]。此外,朱伯龙等[17]采用带翼缘的单层单面墙进行拟静力试验。该方法通过在主体墙体两侧增加翼柱,增大墙体的截面惯性矩,进而提高墙体试件横截面抗弯承载能力,确保墙体在承受最大剪力时不会出现提离现象。但是该试验方法会改变墙体中剪应力的分布,与无翼缘墙体在地震作用下的受力情况并不完全相符。

为了更合理地模拟砌体在地震时所受的垂直荷载与水平地震作用情况,再现地震作用下墙体经常出现的斜裂缝破坏现象,正确测量墙体的初始刚度和抗剪强度,笔者所在课题组创新地提出基于逐级偏压加载的试验方法。该方法能够保证墙体在试验过程中发生剪切破坏,加载过程中通过增加偏心竖向荷载的方式平衡底部拉应力,以防止底部砂浆因受拉开裂造成整个墙体提离,从而发生整体滑移破坏。本文将通过6组砖砌体墙片的拟静力试验,验证该试验方法的有效性和可靠性,并在此基础上进一步研究不同材料和不同构造措施对墙体力学性能的影响。

1 逐级偏压加载平衡拉应力的试验方法

逐级偏压加载平衡拉应力的试验方法是指在进行墙片拟静力试验时,通过在墙片模型左侧逐级增加配重的方式如图1(a)所示,产生一个反向的弯矩,来抵消作动器水平推力在墙体底部产生的拉应力,避免墙片底部受拉发生提离破坏。同时,每个模型共设置2个墙片如图1(b)所示:一方面可减少平面外的效应;另一方面两墙片也可起到互相校核的作用。墙片顶端采用钢筋混凝土盖板进行连接,在盖板上放置配重块来模拟实际墙体受到的重力荷载作用。与常见的千斤顶加载方式相比,该加载方式具有两个方面的优势:一是当墙体试件发生水平侧向位移时,竖向荷载可保持恒定,而使用千斤顶加载时,会产生由摩擦力导致的水平推力增量;二是当墙体试件严重破坏而发生整体微幅下沉时,千斤顶加载系统难以在极短的时间内调节自身行为以保证其与模型不脱离并维持竖向荷载不变,而采用竖向配重加载方法可有效避免这一问题[18]。

试验过程中,墙片模型上存在着两种竖向荷载,分别是作用于墙体中心处的集中荷载以及偏心荷载。作用于墙体中心处的集中荷载对墙体底部左侧边缘产生的正应力,采用公式(1)进行计算。

(1)

式中:Gg为作用于墙体中心处的竖向集中荷载,A为墙体横截面面积。

由材料力学可知:偏心荷载可等效为作用于墙体中心处的集中荷载和弯矩,弯矩采用公式(2)进行计算。

M=GPe

(2)

式中:M为偏心荷载产生的弯矩作用,Gp为偏心荷载产生的竖向集中荷载, e为偏心荷载的合力中心到墙体中心之间的直线距离。

弯矩作用在墙体底部左侧边缘产生的正应力采用公式(3)进行计算。

(3)

式中:M为墙体横截面上的弯矩作用,y为所求应力点到墙体中心的距离,Iz为墙体横截面对中性轴Z的惯性矩。加载时,作动器水平推力会对墙体产生一个弯矩作用,此时墙体底部左侧边缘受到的正应力采用公式(2)和公式(3)进行计算。

2 试验概况

2.1 模型设计与制作

此次试验共设计了6组砌体墙模型,试件的高宽比均为0.65,分别为蒸压粉煤灰砖模型(ZY1和ZY2)、烧结普通砖模型(SJ1和SJ2)和带构造柱的烧结普通砖模型(GZ1和GZ2)。

带构造柱烧结普通砖模型采用“先砌墙,后浇柱”的施工工序,将构造柱钢筋绑扎完成以后开始砌筑墙体,并在柱两侧预留马牙槎,然后整体浇筑模型。墙体由烧结普通砖砌筑而成,为保证其整体性,在墙内每隔四坯砖设置长度为400 mm的水平拉结筋,并伸入构造柱内。构造柱内部共设置4根8 mm×8 mm的麻花状矩形软钢,箍筋选用2 mm的铁丝,箍筋间距为100 mm。考虑偶然性误差,每种模型均制作2个,6组墙片的具体编号、尺寸及构造特点见表1,模型实物照片见图2(a)-图2(f)。

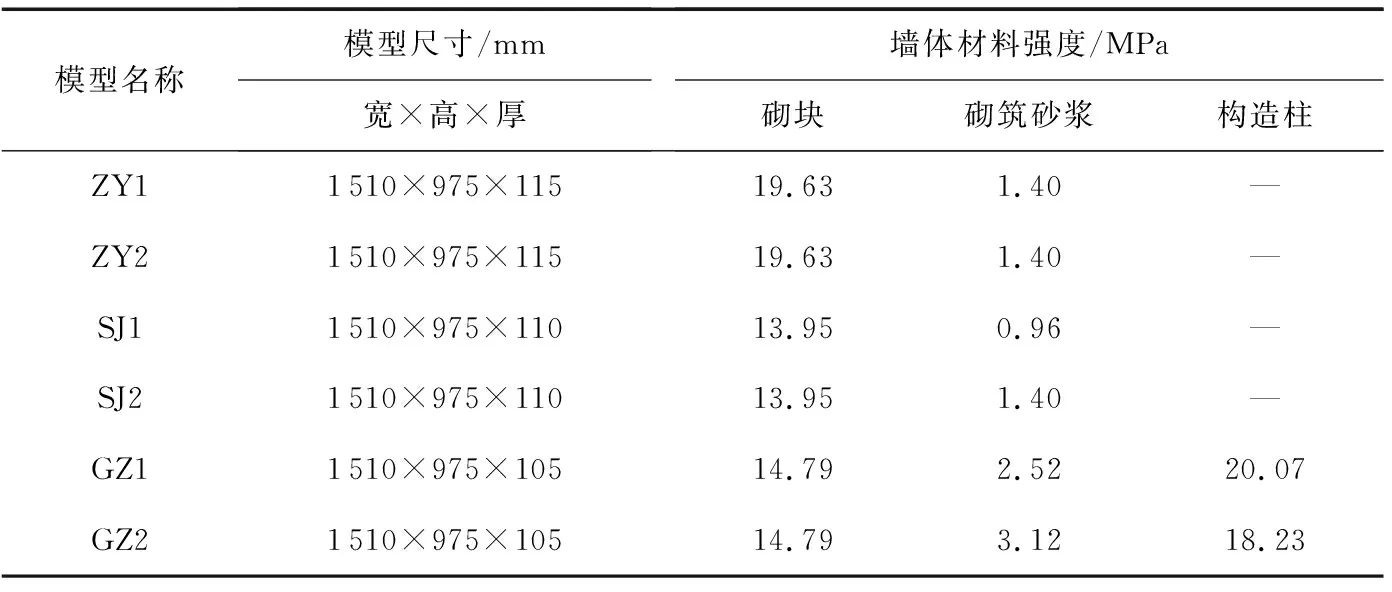
表1 模型尺寸及构造特点Table 1 Model dimensions and configuration

图2 拟静力试验模型Fig. 2 Specimens of pseudo-static

2.2 逐级偏压加载平衡拉应力的试验方法的设计

以模型SJ1试验为例,给出基于逐级偏压加载平衡拉应力试验方法的计算和设计过程。试验初始状态,先在墙体上施加6.0 t配重如图3(a)所示,再将4.4 t重的钢筋混凝土块的合力中心对准墙片中心左侧535 mm处放置,1.0 t重的配重块的合力中心对准墙片中心右侧980 mm处放置如图3(b)所示。同时,最右侧施加的偏心配重不宜过大,防止墙体底部左侧提离。

6.0 t配重对单片墙底部左侧边缘产生的正应力为:

4.4 t偏心配重对单片墙底部左侧边缘产生的正应力为:

首先计算4.4 t配重对单片墙底部左侧边缘产生的正应力:

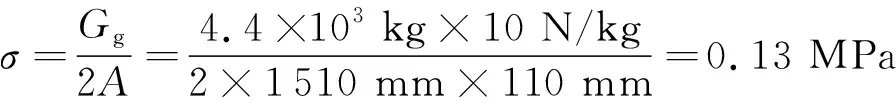
然后计算弯矩作用对单片墙底部左侧边缘产生的正应力:

M=GPe=4.4×103kg×10 N/kg×535 mm=23540000N·mm

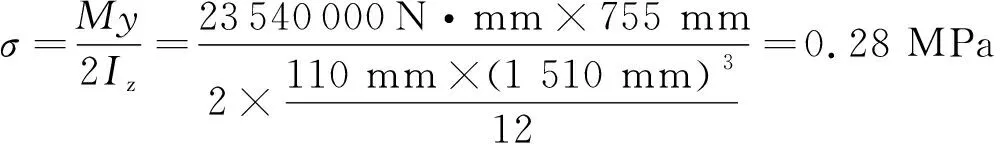
1.0 t偏心配重对单片墙底部左侧边缘产生的正应力为:

首先计算1.0 t配重对单片墙底部左侧边缘产生的正应力:

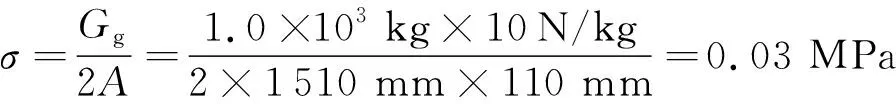
然后计算弯矩作用对单片墙底部左侧边缘产生的正应力:

M=GPe=1.0×103kg×10 N/kg×980 mm=9800000N·mm

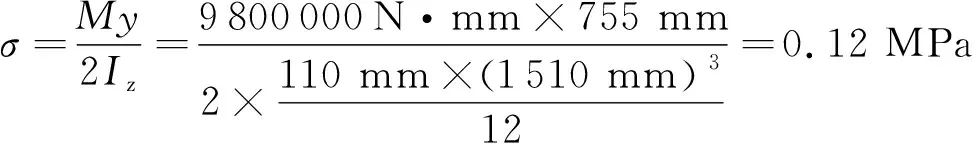
综上所述,初始状态下单片墙底部左侧边缘受到的正应力的理论计算值为0.50 MPa(压应力)。

加载过程中,作动器水平推力Q对单片墙底部左侧边缘产生的正应力为:

求得当作动器水平力推力Q为42.87 kN时,墙体底部的拉应力达到峰值,墙体处于受拉开裂的临界状态。因此,当作动器水平推力为42.87 kN时,在盖板最左端(距离墙体中心1 355 mm)施加0.8 t偏心配重,使墙体底部左侧边缘再次处于受压状态。之后两次加载过程的确定方法同上。逐级偏压加载过程持续三次,当第三次配重加载后,随着位移增大,模型开始出现损伤,荷载增幅较小,但不会发生底部受拉破坏。

2.3 加载方案

基于单侧偏心加载试验方法,采用静力单向水平位移加载的方式。加载过程见图4(a)-图4(d)。当水平力为42.87 kN时,在距离墙体中心偏左1 355 mm处施加0.8t偏心配重如图4(a)所示。当水平力为55.73 kN时,在距离墙体中心偏左1 355 mm处施加1.2 t偏心配重如图4(b)所示。当水平力为68.59 kN时,在距离墙体中心偏左1 355 mm处施加0.6 t偏心配重、距离墙体中心偏左535 mm处施加1.2 t偏心配重如图4(c)所示。第三次配重加完以后,作动器一直加载直至荷载出现下降趋势时停止。

图4 加载过程Fig. 4 Loading processes

2.4 测量方案

试验中测量的物理量包括力和位移,其中作动器的推力和位移由其控制系统反馈获得。如图5所示,水平向加载设备使用的是美国MTS 244.41液压伺服控制系统,该控制系统能够提供精准的力和位移参数。为确保试验所得数据的准确性和可靠性,MTS作动器的推力经过多个方法进行标定[19-20],精度达到0.05 kN。作动器的一端固定在反力架的工字钢梁上,在试验过程中可能因钢梁发生变形而导致模型所需位移数据不准确,进而影响墙片初始刚度的计算。为更精确获得墙片顶端实际水平位移,通过在2片墙的左端各布设一只DT-10型位移计,对墙片的位移进行实时测量,除可以校核作动器的反馈位移外,还能监测模型在加载过程中是否发生扭转。另外,在2片墙可能产生拉应力的左侧底部边缘各布设一只千分表,用于实时监测墙体底部受拉情况。各试验设备型号及详细参数列于表2。并通过人工观测获得墙片各阶段的裂缝开展情况和破坏形态等宏观现象。

表2 试验设备参数Table 2 Parameters of test device

图5 外置位移传感器示意图Fig. 5 Diagram of external displacement sensor

3 试验结果与分析

3.1 破坏模式

选取模型ZY1、模型SJ1和模型GZ1的宏观破坏现象进行介绍。墙片的工作阶段可分为弹性阶段,开裂阶段和破坏阶段[21]。通过对6组墙片的荷载位移曲线进行对比分析发现:在小位移工况下,试件均处于弹性阶段,没有出现损伤,每个工况下荷载和位移呈现线性变化,墙体没有表观裂缝。

随着水平荷载的增加,在工况2.0 mm(水平推力荷载60.91 kN)时,模型ZY1墙体在中部开始出现不连续的水平和竖向微裂缝。随着水平位移增大,墙片沿对角方向产生斜裂缝,裂缝大多数成阶梯型,直至裂缝沿对角线方向贯通,墙体对角线上有少数砖块被剪断如图6(a)所示。

图6 破坏形态Fig. 6 Failure modes

模型SJ1墙体裂缝最早出现在靠近加载点的部位,随着水平推力的增加,在位移1.2 mm工况(水平推力荷载77.70 kN)时,墙片沿对角线中部产生细小的不连续阶梯形裂缝。继续加载,裂缝沿墙片对角线方向不断延伸变宽,直至裂缝沿对角线方向贯通,靠近加载点和墙体对角线上有个别砖块被剪断如图6(b)所示。

模型GZ1墙体裂缝最早出现于墙体中部,随着水平荷载的增加,多条明显的斜裂缝出现,但贯穿于墙体的对角裂缝没有出现。由于高宽比小于1且水平灰缝提供的摩擦力不足,导致墙体局部出现水平裂缝[22]。当层间位移角达到1/55时,砖块也没有出现解体,可见端部构造柱的存在对延性有很大的影响。对比无端部约束构造柱试件,有端部约束构造柱试件除了有水平灰缝和竖向裂缝的开裂、还有较多烧结普通砖的垂直劈裂裂缝如图6(c)所示。

砌体剪切破坏模式主要有3类[23],分别是:1)以砌体沿通缝剪切滑移为代表的剪摩破坏形态。2)以阶梯形斜裂缝为代表的剪压破坏形态。3)以砂浆和块体的劈裂为代表的斜压破坏形态。结合本文所做6组墙体拟静力试验的实际破坏形态,蒸压粉煤灰砖模型和烧结普通砖模型破坏模式为剪压破坏,而带构造柱烧结普通砖模型因构造柱的约束作用,破坏模式为斜压破坏。

3.2 荷载位移曲线

根据MTS作动器反馈的推力和DT-10型位移计反馈的墙片实际位移,绘制各组模型的荷载-位移曲线如图7所示。

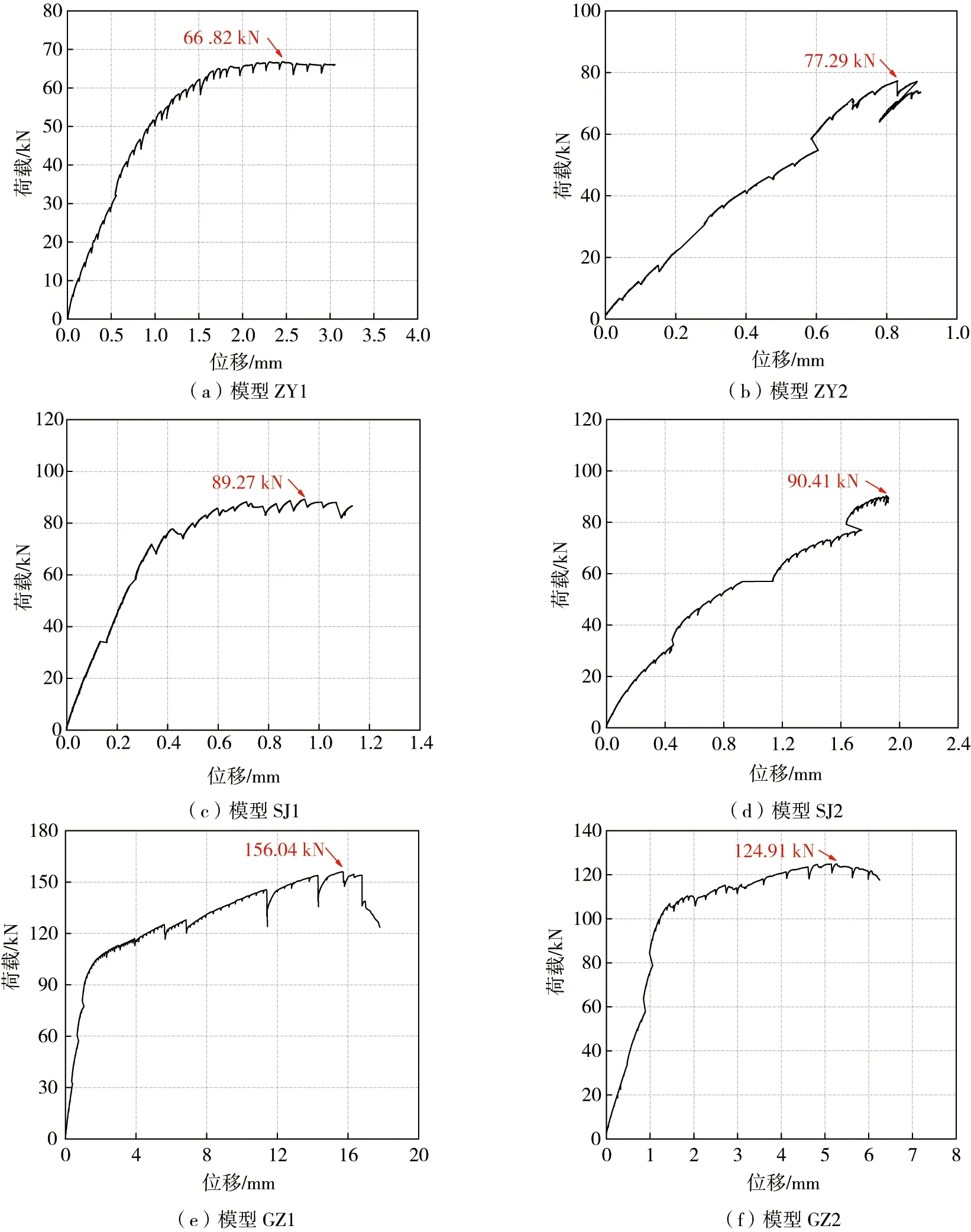
图7 墙片的荷载位移曲线Fig. 7 Load-displacement curves of specimens

6组试件进行拟静力加载时间较长,且要逐级加载,故仅取弹性阶段力、位移数据来分析和计算墙段的初始刚度。

ZY1墙段在加载全过程结束后得到墙段极限位移为3.06 mm,加载过程中最大水平荷载为66.82 kN,取墙段水平位移为0.13 mm和0.56 mm对应的数据计算单片墙段刚度,侧向刚度为26.30 kN/mm如图7(a)所示。ZY2墙段在加载全过程结束后得到墙段极限位移为0.90 mm,加载过程中最大水平荷载为77.29 kN,取墙段水平位移为0.07 mm和0.35 mm对应的数据计算单片墙段刚度,侧向刚度为52.34 kN/mm如图7(b)所示。

SJ1墙段在加载全过程结束后得到墙段极限位移为1.13 mm,加载过程中最大水平荷载为89.27 kN,取墙段水平位移为0.05 mm和0.25 mm对应的数据计算单片墙段刚度,侧向刚度为103.35 kN/mm如图7(c)所示。SJ2墙段在加载全过程结束后得到墙段极限位移为1.93 mm,加载过程中最大水平荷载为90.41kN,取墙段水平位移为0.04 mm和0.37 mm对应的数据计算单片墙段刚度,侧向刚度为34.94 kN/mm如图7(d)所示。

GZ1墙段在加载全过程结束后得到墙段极限位移为17.80 mm,加载过程中最大水平荷载为156.04 kN,取墙段水平位移为0.17 mm和0.51 mm对应的数据计算单片墙段刚度,侧向刚度为43.22 kN/mm如图7(e)所示。GZ2墙段在加载全过程结束后得到墙段极限位移为6.25 mm,加载过程中最大水平荷载为124.91 kN,取墙段水平位移为0.20 mm和0.73 mm对应的数据计算单片墙段刚度,侧向刚度为32.08 kN/mm如图7(f)所示。

表3给出了6组试验模型单片墙的初始刚度、抗剪强度及层间位移角等信息。抗剪强度为墙体的最大水平荷载与横截面面积的比值。

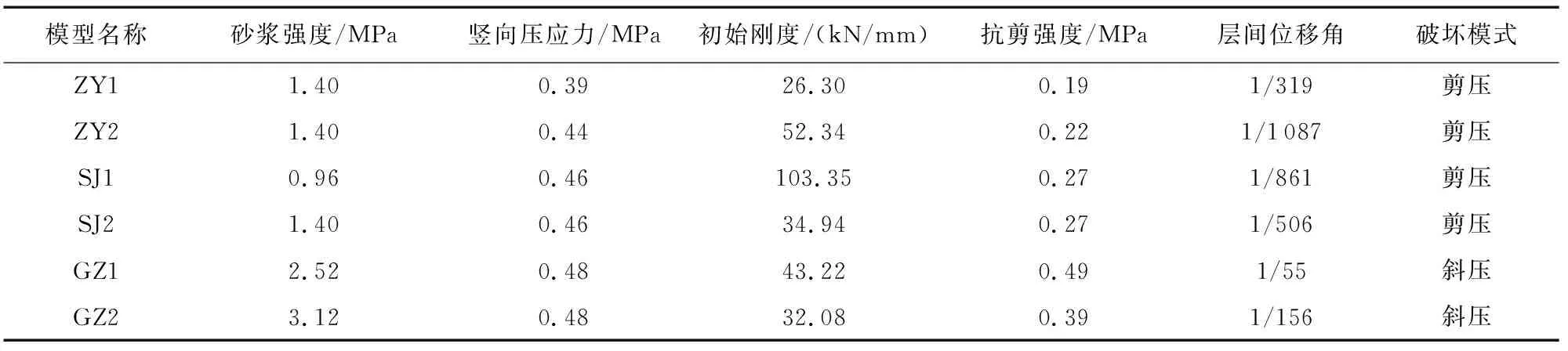
表3 墙片拟静力试验结果Table 3 Pseudo-static results of specimens

对于蒸压粉煤灰砖模型,在砂浆强度相同的情况下,当竖向压应力从0.39 MPa增大至0.44 MPa时,墙体的抗剪强度提高16%,这表明竖向压应力是影响砌体墙抗剪强度的一个不可忽视的重要因素。

与普通烧结砖模型相比,在竖向压应力和砂浆强度基本相同的情况下,蒸压粉煤灰砖模型抗剪强度偏低,约为烧结普通砖模型抗剪强度的81%,变形能力基本相同。试验结果表明:相比于烧结普通砖砌体,蒸压粉煤灰砖砌体抗剪强度低,抗震性能差,建议优先使用烧结普通砖砌筑房屋。

对于带构造柱的烧结普通砖模型,加载结束后的极限位移均在6 mm以上,层间位移角均较高,其中模型GZ1的层间位移角接近钢筋混凝土框架的弹塑性层间位移角限值1/50[24],表明设置端部构造柱后可显著提高墙体的变形能力。此外,构造柱的存在改变了墙体的破坏模式,由素砌体墙片的剪压破坏转变为端部构造柱约束砌体墙片的斜压破坏,表现出一定的延性破坏特征。