基于可调感温电桥的MEMS 传感器恒温控制模型研究
2023-08-12范柚攸周金秋周博远权海洋
范柚攸, 周金秋, 周博远, 张 龙, 权海洋
(1. 北京大学集成电路学院, 北京 100871;2. 北京微电子技术研究所, 北京 100076)
0 引言
传感器作为获取自然和生产领域信息的主要手段, 是人类感官认知的“延伸”。 随着应用水平的深入, 未来传感器将具备微型化、数字化、智能化和网络化等特点[1]。 其中, 微型化的需求催生了MEMS(Micro Electro Mechanical System)传感器的兴起与发展。 因其在尺寸、功耗和成本等方面巨大的优势, MEMS 传感器(包括晶振、压力传感器、加速度计和陀螺等[2])被越来越多应用于各种生活生产场景。 相比传统器件, 精度是制约其向军事、航空和航天等高精尖领域进一步拓展的主要瓶颈,温度是影响MEMS 传感器精度的主要误差来源之一。 MEMS 传感器主要包含敏感结构和处理电路:敏感结构大多采用硅基材料制成, 硅基材料是热敏材料, 温度变化对其杨氏模量、拉伸强度和疲劳强度等机械特性影响很大; 处理电路一般也采用硅基集成电路工艺, 温度波动会引起阈值电压、电阻值和电容值等电学参数的漂移。 机械特性和电学参数的变化最终会造成MEMS 传感器性能的退化, 如何减轻或消除温度波动影响是提高MEMS传感器精度的关键[3]。 目前, 主流的解决方案有两种: 一是温度补偿方案, 二是恒温控制方案。 温度补偿方案[4]通过构造一个MEMS 传感器关键性能参数的温度变化模型, 通过一定的算法对温度引起的误差进行补偿, 操作简单, 补偿效果好, 但是温度补偿方案无法从源头上消除温度波动带来的影响, 且补偿精度与算法复杂度和硬件资源消耗强烈正相关。 恒温控制方案[5-6]需要从封装结构[7]、检测电路[8]和环路控制[9]等三个方面进行设计, 通过闭环控制使电阻或功率管等器件发热,最终将MEMS 传感器工作温度恒定在所需状态,从而减小温度波动对其性能的影响。
许多科研机构都针对MEMS 传感器的恒温控制系统展开了研究, 美国斯坦福大学的Ahn 等[10]基于多环结构设计了一种片上恒温MEMS 陀螺,在封装盖帽层中集成了电阻作为加热器, 根据驱动模态谐振频率检测敏感结构温度, 并通过闭环电路进行控制。 美国密歇根大学的Yang 等[11]提出了一种用于MEMS 惯性模组的恒温控制系统并融入了温度补偿算法进一步提高精度, 该系统使用微机械隔离平台、真空密封和金属封装与周围环境进行热隔离, 采用CMOS 温度传感器和PID 控制方案实现腔体恒温, 并结合最小均方根等补偿算法进行温度补偿。 Hsieh 等[12]提出了一种采用陶瓷封装的小尺寸恒温晶振方案, 通过提高热场分布均匀性在-40℃~85℃范围内实现了±1 ×10-8的频率稳定度。 这些研究工作着重于解决某一特定应用下的恒温控制方案, 对于由封装形式、器件类型和腔体布局等因素变化所引起的温度梯度改变不具有普适意义, 需要重新进行迭代设计。 而且, 大部分恒温控制系统主要关注固定环境温度下的静态控温效果, 对于环境温度动态变化的情况研究较少, 传统恒温控制方案中的控温点受环境温度影响较大, 限制了其在高精度方面的应用。同时, 恒温控制方案是电学和热学的复合物理场仿真, 文献中对于热电一体化模型的研究也相对较少, 无法给设计者提供有工程价值的指导。 本文针对温度梯度和环境变化两个问题, 提出了一种可调感温电桥结构, 以低成本的电学调整方式适应多梯度的应用条件, 增加了环境温度反馈控制以提高恒温控制模型的环境温度鲁棒性。 根据模型数学关系推导, 本文基于Simulink 建立了热电一体化模型, 并针对热阻、热容、环境温度、控温电阻等关键参数进行了仿真分析, 验证了模型的可行性和准确性。
1 可调感温电桥恒温控制方案
不同于其他电学设计对于散热效果的追求,恒温控制方案需要在相对密闭的腔体环境中实现,且腔体的热阻要满足一定要求。 这样的设计既有利于降低加热器件的功耗, 又有利于减小外部环境对腔体内部的影响。 恒温控制环路是由电路径和热路径共同构成的负反馈环路, 而热路径上的关键器件就是温度传感器, 温度传感器将热信息转换为电信号, 再由控温电路对电信号进行处理。最终稳定温度是加热功率与散热功率之间的动态平衡, 加热功率可以由电学环路加以控制, 散热功率则与腔体材料、尺寸和布局等相关, 不同散热功率需要相应的加热功率进行匹配。 由于热阻与导热系数成反比, 与结构厚度成正比, 为了避免热量耗散, 需要选用导热系数小的材料进行隔热处理, 并在合理尺寸范围内增大隔离材料厚度。恒温腔体中集成分布有加热器件、敏感结构和温度传感器等, 热量传递和稳定具有时间迟滞, 腔体内器件的布局差异就会造成温度梯度, 从而影响系统恒温点的控制效果。 热学模型建立过程复杂且与电路联合仿真困难, 导致恒温控制系统需要经过多次实际加工迭代后才能确定。 器件和封装变化又会破坏恒温腔体原有的温度梯度分布状态从而造成目标控温点漂移, 传统恒温控制系统需要重新设计以满足新的热学要求, 设计缺乏灵活性且周期冗长。 本文提出的恒温控制模型同时监测腔体中两个点的温度(加热芯片Tchip和热敏电阻Tres), 调整这两个温度的加权函数控制腔体温度Toven达到目标值。 加权系数的修正以可调感温电桥为核心, 通过快速电学参数调整适应不同热环境下的恒温控制需求。 在腔体外进一步监测环境温度Tamb的波动, 作为修正量增加到加权函数中抑制其对腔体恒温点的影响。
图1 为恒温控制方案的具体实现原理图, 该方案包括可单片集成的核心控制电路和两个热敏电阻。 核心控制电路、热敏电阻RToven和敏感结构都集成封装于密闭真空腔体中, 进一步降低了热对流造成的热量损耗。 腔体与另一个热敏电阻RTamb通过PCB 板进行电学连接, PCB 板上还集成了必要的电源管理芯片、微处理器芯片和电容电阻器件, 最终可实现MEMS 传感器的高精度应用。 核心控制电路由恒温控制环路和环境温度抑制电路构成, 采用PN 结或热敏电阻感知温度变化, 构建热路径和电路径组成的闭环。 恒温控制环路中,除了热敏电阻RTres外, 其余器件均在片上集成,R1、R2、R3、RT和I1、I2组成了感温电桥。I1、I2为带隙基准电路中的正温度系数电流的镜像电流,与温度呈正相关, 满足如下关系
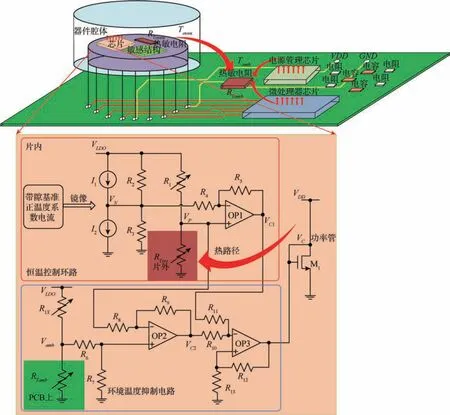
图1 可调感温电桥恒温控制原理图Fig.1 Schematic diagram of adjustable temperature sensing bridge oven-controlled
式(1)中, ΔVbe为两个PN 结电压差值, 与温度呈正比关系, 该电压经过电阻RX转化为正温度系数电流;k为玻尔兹曼常数,q为电荷常数,N为带隙基准中两个晶体管的尺寸比值。I1和I2之间的电流关系可以进行调节, 通过抽取或灌入电流改变VN节点的电压。R2、R3和I1、I2组成了感温电桥的一条桥臂共同决定VN节点电压,VN节点电压可以表示为
式(2)中,VLDO为由带隙基准电压产生与温度弱相关的电压,R2、R3、RX采用温度特性相同的电阻类型, 通过比例关系消除温度对阻值变化的影响。 因此,VN节点电压与温度呈一次函数关系,函数斜率方向和大小均可通过λ进行调整。
R1和RT组成了温度电桥另一条桥臂,R1采用温度系数较小的电阻, 忽略温度对其阻值的影响,R1阻值对控温点有影响设计成阻值可调。RT为片外热敏电阻, 电阻阻值和测温精度都较高, 本文采用负温度系数的热敏电阻, 其阻值经分段拟合后可以表示为
R1和RT共同决定VP节点电压,VP和温度负相关, 可以表示为
恒温控制的目的是使敏感结构工作在合适的温度点, 两个电桥分别采用PN 结检测包含温控电路的芯片温度波动和采用热敏电阻检测腔体温度变化, 由于腔体中温度梯度的存在, 这两个参数都无法单独表征敏感结构的温度, 感温电桥和运算放大器OP1 输出一个加权值VC1表示敏感结构温度信息
加权电压VC1包含了芯片内部温度信息和外部热敏电阻温度信息, 可以作为控制加热功率管的信号。R1阻值和电流源比例λ可以通过寄存器设置或熔丝烧调等电学方式进行参数选择, 从而实现不同温度梯度下的控温点稳态值调整。 恒定温度控制回路的工作原理如下: MEMS 传感器刚上电工作时, 热敏电阻RT阻值较大,VP大于VN,VC1增加, 功率管开启加热使腔体温度升高。 随着温度升高逐渐接近目标温度, 热敏电阻RT阻值降低,VN和VP之间差值减小,VC1减小, 加热电流减小,加热功率与散热功率平衡时腔体温度到达稳态。单回路控制方案在环境温度不变的情况下有较好的控制效果, 但是如果环境温度波动, 由于热阻的存在会引起腔体温度的变化, 这种情况在环境温度剧烈变化的情况下更为显著。 因此, 参考开关电源中纹波采样补偿的思想对环境温度进行采样, 以PCB 板上的热敏电阻RTamb感知环境温度,构建与恒温控制环路中VP相似的电桥结构, 比较Vamb和VP电压得到温度变化误差信息VC2, 表达式为
式(6)中,R9=2R8,R6=R7,R1X的取值与R1有关, 也可以通过电学方法调整。 将电阻关系代入式(6)中, 可得
将VC1和VC2进行融合得到控制功率管的信号VC, 其表达式为
式(8)中,R10=R11=R12=R13。 将电阻关系代入式(8)中, 可得
VC作为功率管控制信号决定了加热电流的大小, 加热电流是与VC相关的函数, 具体表达式与功率管控制方式有关, 可以表示为
恒温控制环路是通过热路径形成闭环的, 功率管是热量的主要来源, 功率管产生的功率一部分在散热路径消耗掉, 另一部分被腔体吸收提高腔体温度。 温度变化的过程主要由热阻RH和热容CH两个物理量决定, 根据材料特性、器件布局和封装形式等通过集总模型或分布式模型求解得到。根据能量守恒定理, 腔体温度变化方程可以表示为
式(11) 中,Pheat为功率管加热产生的总功率,m为等效质量,Toven为腔体目标恒温温度,Tamb为环境温度,kC为与热容相关的比例系数,kR为与热阻相关的比例系数。 式(11)中, 右侧第一项为腔体吸收热量的微分(目标温度和环境温度都是时变函数), 即腔体温度升高所需的功率, 与热容相关;右侧第二项为腔体的散热功率, 与热阻有关。 功率管的发热功率可以表示为加热电流与电源电压的乘积, 则式(11)可改写为
根据式(11)和式(12), 可以通过功率管加热电流将电学部分和热学部分联系起来, 从而建立热电一体化模型分析优化性能。
2 模型建立和参数选择
基于上节理论分析建立了如图2 所示的热电一体化恒温系统Simulink 仿真模型, 紫色虚线框内为电学部分, 绿色虚线框内为热学部分。 电学模型抽象了温度引起的电压变化并控制功率管输出加热电流的过程, 加热电流作为热学模型的输入经微分方程计算后产生温度信号, 通过热反馈路径作用于电学模型中的温度传感器, 形成热电一体化闭环模型。 为了更真实反映电路模型的影响,电学部分加入了电压限位模块将电压信号限制在0 ~VDD范围内, 加入了零极点模块用以模拟运算放大器的动态特性, 并在电流输出处加了电流限位模块用以限制加热电流的范围, 防止过大电流和负电流的出现使其符合功率管的实际工作状态。模型中, 还引入了延迟模块用以模拟不同温度梯度分布情况, 环境温度是与仿真时间相关的函数,通过环境温度设置模块将其波动影响纳入模型中。
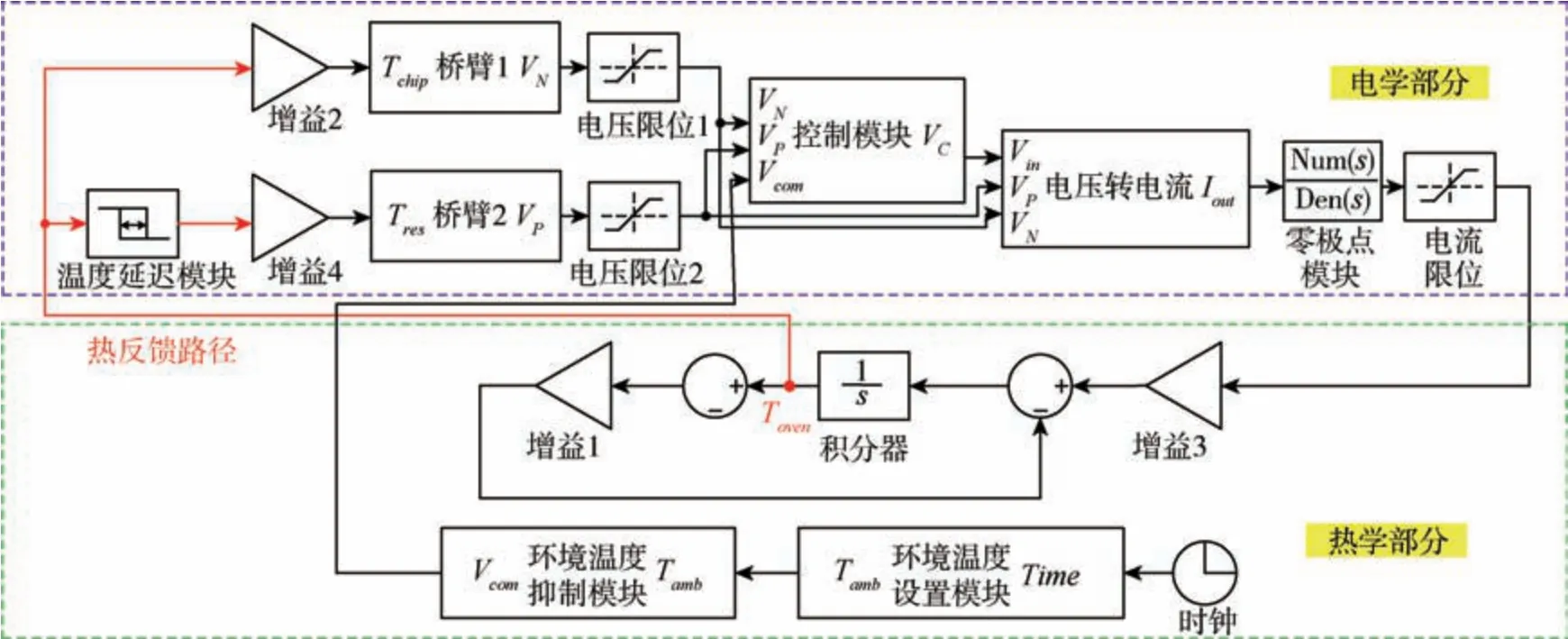
图2 热电一体化的恒温控制系统Simulink 仿真模型Fig.2 Simulink simulation model of thermal-electronic integration oven-controlled system
恒温控制系统仿真模型需要确定的主要参数有目标控制温度、热阻、热容和加热功率等。 目标控制温度要根据敏感结构的温度特性决定, 以晶振为例, 其谐振频率温度曲线近似为三次曲线,频率最稳定的温度范围为75℃~95℃, 因此本文的目标控制温度设定在此范围内。 热阻和热容的影响因素很多, 包括腔体材料选择、尺寸设计、器件布局等, 这些因素会引起热传导路径和散热效率的变化。 热阻是物体散热能力的体现, 热阻越大散热能力越差, 对于恒温系统而言, 热阻越大, 所需维持控温平衡的加热功率越小, 系统功耗降低。 由于作为热源的控温芯片与敏感结构封装在同一腔体中, 做好腔体的整体隔热就可以降低热量损失, 腔体的热阻可以近似等效为隔热材料的热阻。 表1 列出了几种可作为腔体隔热材料的导热系数和热阻, 本文设计的隔热组件厚度在毫米(mm)量级, 以3mm 为例计算材料热阻。
腔体从常温到目标控温点所需温升约为60℃,功率管可提供的输出功率范围为0.5W~3.0W, 因此仿真时设置的热阻范围为20℃/W ~120℃/W。热容范围可以针对几种实际封装形式加电流测试其温度变化数据, 再根据热阻范围拟合数据得到, 本文热容仿真范围设置为0.05J/℃ ~0.25J/℃。 为了缩短达到恒温点的时间, 本文设计的恒温系统加热初期采用最大功率恒定电流加热, 随着腔体温度逼近控温点, 加热电流切换为VC控制下的功率管电流输出, 根据功率管的输出功率(0.5W~3.0W) 和电源电压(5V), 仿真设置的最大加热电流为600mA。 上文分析了热电一体化恒温系统Simulink 仿真模型中几个主要参数的范围选择, 下一节将在此范围内对模型性能进行详细研究。
3 实验结果
3.1 恒温点的确定
恒温控制环路最终稳定的判据为VN-VP=Vos,Vos为运算放大器的失调电压, 常见运算放大器的失调电压约为几到几十毫伏(mV), 最终恒温点为R1和λ的二维函数T(R1,λ), 根据T(R1,λ)可以计算恒温点的理论值。 恒温点仿真值通过Simulink模型仿真得到, 主要仿真参数设置如下:RH=50℃/W,CH=0.1J/℃, 环境温度为25℃, 最大加热电流为600mA,R1阻值扫描范围为500Ω ~2500Ω,λ扫描范围为0 ~2。 图3 为R1和λ对恒温点的联合影响结果, 随着R1阻值的减小和λ的增加, 恒温点逐步升高。 对比恒温点的理论值和仿真值, 其变化趋势一致, 平均误差为1.4%。
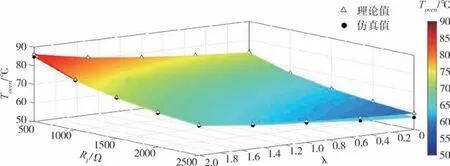
图3 R1 和λ 对恒温点的联合影响Fig.3 Joint influence of oven-temperature point by R1 and λ
由图3 可知,R1和λ对恒温点的影响程度是不同的, 分别扫描R1和λ并计算其温度灵敏度。图4 为R1和λ分别对恒温点的影响程度曲线, 将R1和λ的变化归一化后可以看出,R1和λ对恒温点的影响方向是相反的, 且R1的影响程度更大。λ的影响曲线比较线性, 其对温度响应的灵敏度(即斜率)为0.05。R1的影响曲线呈现出了较强的非线性, 分段求解其斜率, 分别为-0.48(从-100%变化到-75%区间)、-0.18(从-75%变化到-15%区间)和-0.07(从-15%变化到100%区间), 每个区间的斜率均比λ的影响曲线的斜率大, 分别是其9.6 倍、3.6 倍和1.4 倍。 因此, 在调整恒温点时R1的灵敏度比λ的灵敏度大。 实际应用中, 可以实现恒温点的粗调和细调。
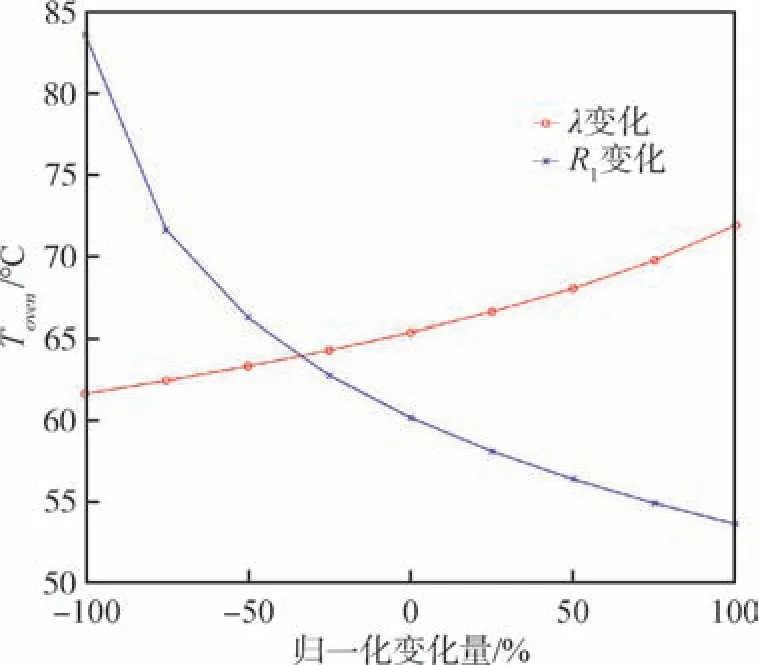
图4 R1 和λ 对恒温点的影响程度曲线Fig.4 Influence level curves of oven-temperature point by R1 and λ
3.2 热阻热容的影响
热阻和加热功率是相互制约的参数, 热阻越大, 维持目标控温点所需加热功率越小。 主要仿真参数设置如下:CH=0.1J/℃,R1=500Ω,λ=1.5, 环境温度为25℃, 最大加热电流为600mA,RH扫描范围为10℃/W ~90℃/W。 图5(a) 为热阻与恒温点的关系曲线, 热阻的变化不影响恒温点,五种热阻情况下恒温点均为79.69℃。 但是, 热阻越小, 到达恒温点的时间越长, 随着热阻增加热量损失降低, 时间差异不再明显。 图5(b) 描绘了热阻与加热功率的关系, 热阻越大加热功率越小,有利于降低系统功耗。
热容表征了腔体吸收热量的能力, 热容越大,相同温升下需要越大的加热功率。 主要仿真参数设置如下:RH=50℃/W,R1=500Ω,λ=1.5, 环境温度为25℃, 最大加热电流为600mA,CH扫描范围为0.05J/℃~0.25J/℃。 图6(a)为热容与恒温点的关系曲线, 热容的变化不影响恒温点, 五种热容情况下恒温点均为79.69℃。 图6(b)描绘了热容和加热功率的关系, 系统达到恒温点所需时间与加热功率均与热容呈正比, 与电容相似, 热容越大, 恒温点瞬态过冲现象有所改善。
3.3 环境温度的影响
由式(12)可知, 如果环境温度随时间变化而非常量时, 加热电流会发生变化从而造成恒温点的波动。 本文在恒温控制环路基础上增加了环境温度抑制电路, 在环境温度变化的条件下对有无此电路的两种情况进行了仿真对比。 主要仿真参数设置如下:RH= 50℃/W,CH= 0.1J/℃,R1=500Ω,λ=1.5, 最大加热电流为600mA, 环境温度的波动范围设置为-55℃~55℃, 波动方式为阶跃变化和斜坡变化。 阶跃变化的温度点为-55℃(0s~30s)、0℃(30s~40s)、25℃(40s ~50s)、55℃(50s~60s)、15℃(60s~70s)和-25℃(70s ~100s),斜坡变化的环境温度以1.1℃/s 的斜率在100s 内从-55℃变化到55℃。
图7 比较了阶跃变化时环境温度抑制电路的作用。 红线为无抑制电路时的腔体温度变化, 控温点随着环境温度波动而变化, 最大温度改变量为1.41℃, 控温点稳定度为1.7272 ×10-4/℃。 蓝线为抑制电路起作用时的控温点变化, 最大温度改变量为0.03℃, 控温点稳定度为3.69 ×10-6/℃,控温点稳定度提升了46.8 倍。
图8 比较了斜坡变化时环境温度抑制电路的作用。 红线为无抑制电路时的腔体温度变化, 控温点随着环境温度升高而升高, 最大温度改变量为1.32℃, 控温点稳定度为1.5373 ×10-4/℃。 蓝线为抑制电路起作用时的控温点变化, 最大温度改变量为0.028℃, 控温点稳定度为3.25 ×10-6/℃,控温点稳定度提升了47.3 倍。
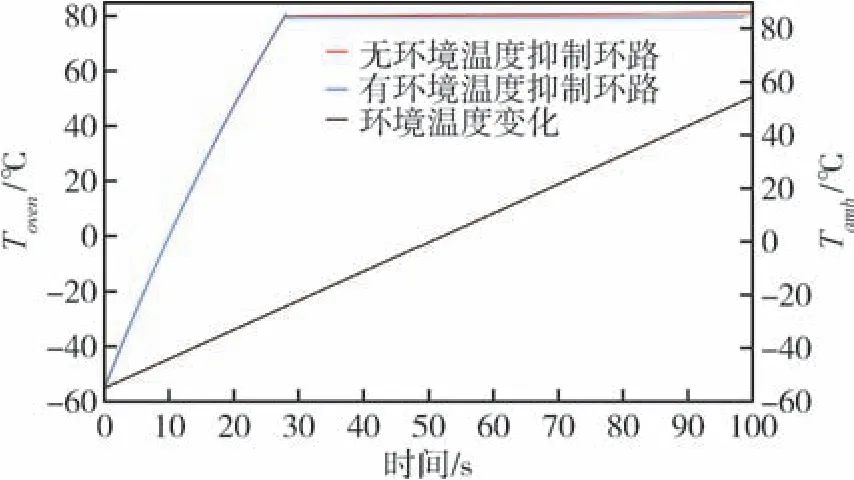
图8 环境温度斜坡变化时的影响Fig.8 Influence of ambient temperature slope variation
恒温点的建立时间与MEMS 惯性传感器的启动时间具有较强相关性, 恒温环境越快建立越利于传感器的稳定工作。 不同热阻、热容和环境温度都会造成建立时间的差异, 考虑功耗的限制,恒温系统的热阻需要满足热平衡条件, 结合图5(a)可知, 热阻大于30℃/W 后对于建立时间的影响并不大。 因此, 本文主要考虑热容和环境温度对于恒温点建立时间的影响, 主要仿真参数设置如下:
RH= 50℃/W,CH= 0.05J/℃ ~ 0.25J/℃,R1=500Ω,λ=1.5, 最大加热电流为600mA, 环境温度设置五个温度点( -55℃、-25℃、0℃、25℃和55℃), 仿真结果如表2 所示。 从仿真数据可以看出, 热容增大会导致恒温点的建立时间变长, 环境温度的影响则是相反的, 环境温度越高即与恒温点温差越小, 恒温点的建立时间越短。
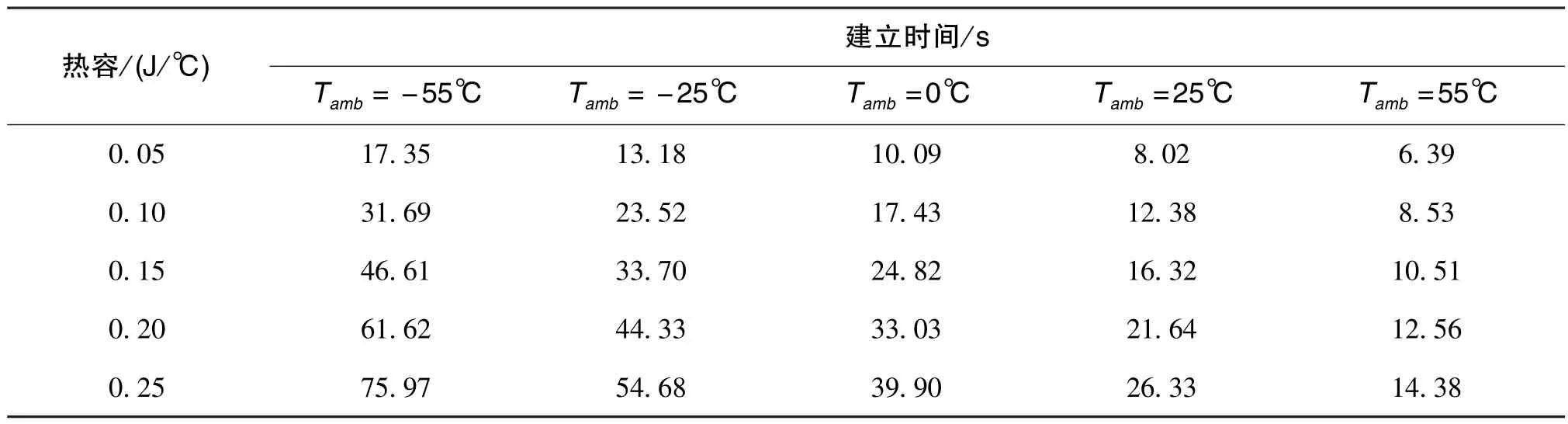
表2 热容和环境温度对恒温点建立时间的影响Table 2 Influence of oven-temperature point setting time by thermal capacity and ambient temperature
3.4 不同温度梯度的恒温点调整
本文提出的恒温控制方案提供了两个便于调整恒温点的电学参数R1和λ, 调整匹配这两个参数可以解决一定范围内由于封装形式和腔体布局等带来的温度梯度问题。 为了模拟不同温度梯度分布情况, 模型中引入了温度延迟模块使腔体中控温芯片、敏感结构和热敏电阻处同一时刻具有不同的温度。 主要仿真参数设置如下:RH=50℃/W,CH=0.1J/℃, 最大加热电流为600mA, 环境温度为25℃。 设置五种不同温度梯度情况, 扫描R1(500Ω~2500Ω)和λ(0 ~3)得到的结果如图9 所示。图9 展示了五种温度梯度分布下R1和λ取值组合的恒温点及其等温图, 对于本文仿真的目标控温点79.69℃, 五种温度梯度情况下的电学参数取值列在表3 中, 各梯度下恒温点与目标温度误差小于0.1%。

表3 不同温度梯度下同一恒温点的电学参数取值Table 3 Electrical parameter values at the same oven-temperature point under different temperature gradients
4 结论
本文针对高精度MEMS 传感器的应用提出了一种基于感温电桥的恒温控制优化方案, 该方案在传统恒温控制环路中加入了环境温度抑制电路,降低了环境温度波动对恒温点的影响。 同时, 为了解决不同温度梯度情况下恒温点的调整问题,本文在恒温控制环路中设计了方便可调的电学参数, 通过寄存器设置或熔丝烧调即可修正恒温点,而无需再迭代设计。 本文根据电路实现方案和热学微分方程抽象了热电一体化的Simulink 模型, 分析了主要设计参数的选值范围并进行了仿真验证,此模型对恒温点控制的理论值与仿真值误差为1.4%。 本文针对环境温度变化( -55℃~55℃)采用了阶跃和斜坡两种方式进行了模拟: 阶跃变化时增加了环境温度抑制电路的模型, 相比未加该电路的模型, 控温点的温度稳定性从1.7272 ×10-4/℃降低到3.69 ×10-6/℃, 优化提升了46.8倍; 斜坡变化时增加了环境温度抑制电路的模型,相比未加该电路的模型, 控温点的温度稳定性从1.5373 ×10-4/℃降低到3.25 ×10-6/℃, 优化提升了47.3 倍。 电学参数R1和λ提供了不同的调整能力, 可实现对恒温点的粗调和细调功能, 经仿真在五种温度梯度分布情况下均可使腔体温度达到相同恒温点。 本文提出的恒温控制方案具有更广泛的适用性, 降低了设计难度, 缩短了设计周期,有利于恒温控制方案在高精度应用中的推广。
