爆炸荷载下路堑岩质边坡振动效应研究*

宿利平,王 宁,杜连杰,高玉龙,张小军,高文学

(1.北京市政路桥股份有限公司,北京 100045; 2.北京工业大学城市建设学部,北京 100124)

0 引言

目前,已有众多学者从理论分析、数值模拟和现场试验等多个角度研究边坡岩体爆破及其振动效应。张小军[1]从弹性波在介质中传播的角度,研究爆破振动在台阶地形中的传播规律,推导出适合预测台阶地形的爆破振动公式;范道林等[2]根据叶巴滩水电站岩石高边坡爆破振速预测公式分析了边坡爆破振动传播规律,得出不同方向振动衰减规律;张云鹏等[3]通过数值模拟探究振动频率对边坡岩体质点振动速度传播规律的影响,得出质点峰值振动速度受地形高程和振动频率共同影响的结论;孙鹏昌等[4]基于赤湾山单薄山体双面岩质边坡爆破振动实测数据,从幅值、持续时间及频率方面分析了迎爆侧坡面和背爆侧坡面的振动规律,并提出了相应的安全控制措施;厉美杰等[5]结合露天矿山爆破振动监测数据,对爆心距和单响药量进行敏感性分析,得出爆心距对爆破振动速度的敏感性较高,并结合实际情况提出相应的施工方法;马晨阳[6]采用LS-DYNA有限元软件分析不同爆心距、不同坡度、不同水深条件下岸库边坡的振动响应,揭示水下钻孔爆破边坡变形演化机制;欧阳建华等[7]通过对边坡岩体爆破振动跟踪监测分析,得出凸性边坡岩体存在高程放大效应。

本文以国道109新线高速公路路堑边坡岩体爆破工程为背景,基于爆破振动监测并结合数值模拟,分析边坡岩体关键部位爆破振动特征。

1 路基石方爆破与振动监测

1.1 工程概况

国道109新线高速路基工程(K60+254—K78+400段)以石灰岩、安山玢岩、斑岩为主,其抗压强度介于30～60MPa,为中硬岩体。K71+200—K71+240段路堑岩体开挖设计为三级边坡,其中第一、二级边坡已开挖完成,第三级边坡已开挖4m,该台阶剩余部分(高6m)拟采用爆破开挖,如图1所示。

图1 测点布置(单位:m)

1.2 爆破参数设计及振动监测

爆破设计参数:台阶高度H=6m,炮孔直径φ=90mm,超深Δh=1m,炮孔深度h=7m,采用倾斜钻孔;孔距a=3m,排距b=2.5m,抵抗线W=2.8m;选用乳化炸药,炸药单耗q=0.3kg/m3。采用逐孔起爆方式,孔间与排间延时分别为10,100ms。

测点位置布置如图1所示。对现场爆破振动监测数据进行整理分析,如表1所示。其中,4号测点质点峰值振速及频谱特征如图2所示。

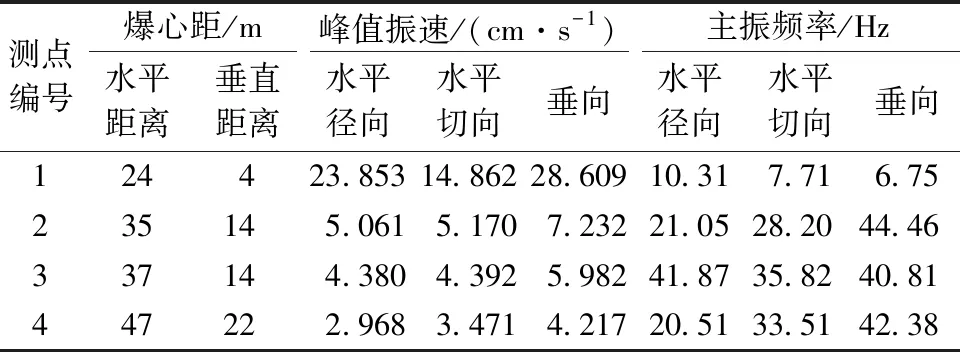
表1 爆破振动监测结果

图2 4号测点振速及频谱特征

1.3 爆破振动规律分析

峰值振动速度是描述爆破振动强度的重要指标,由于考虑地形条件及其随高程的变化,因此对于高差较大边坡,本文采用下式[8]对边坡质点峰值振速衰减规律进行拟合:

(1)

式中:k为与地质条件相关的系数;v为质点峰值振速(cm/s);Q为最大单响药量(kg);R为水平距离(m);H为垂直距离(m);α为地震波衰减系数;β为高程影响系数。

基于式(1)拟合结果为:

其中,各方向拟合复相关系数R2分别为0.997,0.987,0.994,表明拟合结果有较高可靠度。

将表1中的各测点峰值振速数据整理得到测点峰值振速与水平距离、垂直距离关系,如图3所示。

图3 测点峰值振速衰减曲线

由图3可知,质点峰值振速随爆源距离增加而衰减,但各向分量的动力响应不同,垂直峰值振速大于水平径向和切向。

除1号测点距爆源太近,质点峰值振速较大外,其余测点质点峰值振速均<8cm/s,各方向主振频率在10～50Hz,其峰值振速满足GB 6722—2014《爆破安全规程》规定的8～12cm/s的振速安全阈值,因此可认为边坡岩体处于安全状态。

2 边坡爆破振动数值模拟

2.1 数值模型

数值模型的岩体类型为中风化正长斑岩,坡面岩体为理想的弹塑性体。岩体物理力学参数为:弹性模量29.13GPa,重度26.2kN/m3,泊松比0.26,内摩擦角55°。

现场爆破试验边坡岩体为中风化正长斑岩,第三级台阶部分岩体已开挖完成。炮孔及其周围的岩体网格单元尺寸为0.05m,坡面网格单元大小为0.3m,在模型边界处为1.5～3m,岩体内部采用线性梯度的网格单元大小平滑过渡,数值计算模型尺寸如图4所示。

图4 边坡数值计算模型(单位:m)

2.2 等效爆破荷载

根据圣维南荷载等效原理[9],将炮孔壁的峰值压力等效为在同一排炮孔中心线上均匀分布。等效爆破荷载的峰值压力pm计算公式为:

(2)

(3)

式中:ρ0为装药密度;D为炸药爆轰速度;φ为药包直径;a为炮孔间距;d为炮孔直径;γ为等熵指数;p0为爆轰波产生的平均初始压力。

等效爆破荷载简化为三角形荷载曲线[10]。计算爆破荷载压力的升压时间为:

(4)

计算爆破荷载压力的正压时间为:

(5)

由式(5)得到峰值压力大小为pm=7MPa,爆破荷载升压时间为2ms,正压作用时间为7ms。

2.3 数值模拟结果分析

2.3.1数值模拟可靠性分析

在数值模型中提取与现场监测测点对应位置的质点峰值振速模拟值,并计算与实测值间的相对误差,相对误差结果如表2所示。由表2可看出,相对误差大部分在10%以内,表明模拟结果具有一定的可靠性。因此,现场试验条件有限的情况下,利用数值模拟可对工程中的许多问题进行分析,优化爆破设计,指导工程施工。

表2 PPV模拟结果与实测结果对比

2.3.2质点振动速度分析

爆炸荷载作用下不同时刻边坡水平径向振动速度云图如图5所示。

图5 爆破振速云图

提取坡面各质点3个方向的峰值振速,坡面峰值振速变化曲线如图6所示。由图6可看出边坡坡面各质点在爆破荷载作用下,质点峰值振速随水平距离的增加总体呈衰减趋势。在同一级边坡台阶平面处,受“鞭梢效应”[11]影响,台阶外缘质点峰值振速明显大于台阶内侧2m范围内质点峰值振速,将峰值振速放大倍数定义为台阶外缘与坡脚处峰值振速之比,峰值振速放大倍数如图7所示。

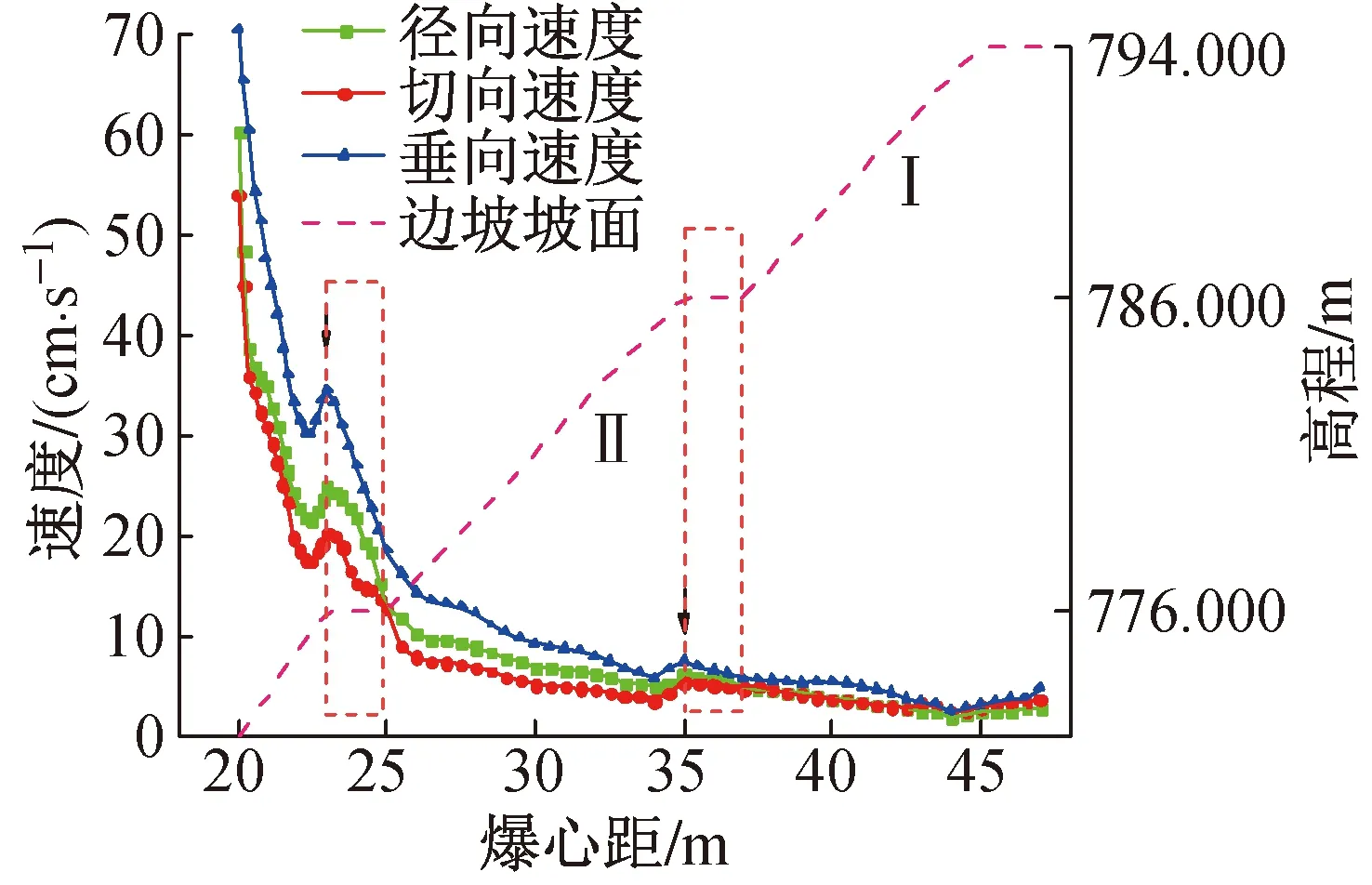
图6 峰值振速沿坡面变化曲线

图7 峰值振速放大倍数

由图7可得到在高程为776.000m台阶平台处,即第二级台阶的径向、切向、垂向峰值振速放大倍数分别为1.951,1.595,1.862,在高程为786.000m台阶平台处,即第一级台阶的径向、切向、垂向峰值振速放大倍数分别为1.297,1.134,1.223,径向和垂向质点峰值振速放大倍数大于切向的峰值振速放大倍数。第二级台阶靠近爆源,峰值振速放大倍数更大。因此,可认为边坡台阶距离爆源越近,峰值振速放大倍数越大。

3 不同坡度爆破振动效应分析

为进一步研究路堑边坡爆破振动效应,分别建立边坡台阶高度均为10m,边坡坡度为1∶0.3,1∶0.5,1∶0.75及1∶1的边坡岩体爆破数值模型,并由三级边坡推广至五级边坡,边坡岩体力学参数与爆破荷载施加方法同2.1节和2.2节。其中,边坡各模拟测点均设置于台阶外缘,边坡坡度为1∶0.5的数值模型和各模拟测点布置如图8所示。

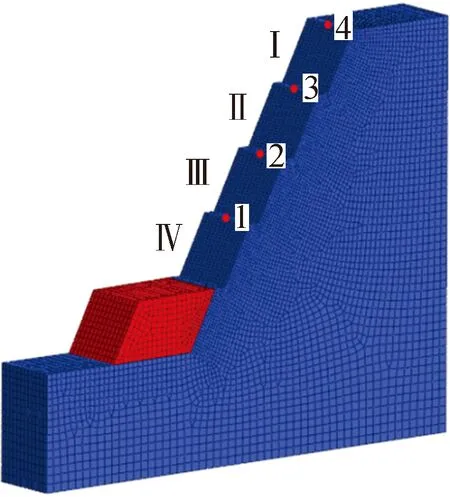
图8 坡度1∶0.5模型

提取不同边坡坡度条件下各模拟测点峰值振速,结果如图9所示。

图9 不同坡度下各测点峰值振速模拟值

根据图9可知,在边坡坡度为1∶0.3,1∶0.5,1∶0.75,1∶1时,坡面顶端4号测点质点峰值振速相较于第一级台阶平面外缘3号测点有明显的高程放大效应,放大倍数分别为1.05,1.13,1.12,1.06。各模拟测点峰值振速随边坡坡度的增大而增大,在坡度为1∶0.3时峰值振速达到最大,坡面顶端4号模拟测点的质点峰值振速达到5.55cm/s,是边坡坡度为1∶0.5时质点峰值振速的1.61倍,边坡坡度为1∶0.75时质点峰值振速的2.44倍,边坡坡度为1∶1时质点峰值振速的3.43倍。结合边坡爆破施工,边坡表层岩体风化程度较严重,岩体类型多为强风化岩石,岩层稳定性较差,若上级边坡坡度设计较大,下级边坡岩体爆破施工产生的爆破振动会对路堑边坡的稳定性造成一定程度的破坏。因此,在边坡坡度设计时,上级边坡坡度可设计较缓,以减小爆破振动对上级边坡产生的不利影响。

4 结语

1)边坡质点峰值振速随爆源距离的增加而衰减,但各向分量的动力响应不同,垂向峰值振速大于水平径向和水平切向。

2)同一级台阶平台处,受“鞭梢效应”影响,台阶外缘质点峰值振速大于台阶内侧2m范围内质点峰值振速;台阶外缘质点峰值振速相较于坡脚处峰值振速放大倍数,随台阶与爆心距离增加而减小。

3)随着边坡坡度增大,各级边坡台阶外缘质点峰值振速呈增大趋势,坡面顶端质点峰值振速在坡度为1∶0.3时达5.55cm/s,为边坡坡度1∶1时的3.43倍,结合边坡表层岩体风化程度较严重,故路堑边坡设计(特别是上级边坡)应综合考虑岩体地质条件的变化及爆破振动对边坡稳定性的影响。