径流变异对黑河流域上游径流统计特征与频率分析的影响

2023-08-09席海潮解阳阳刘赛艳黄成剑

灌溉排水学报 2023年7期

席海潮，解阳阳,2*，刘赛艳，黄成剑，沈腾，张钦

（1.扬州大学水利科学与工程学院，江苏扬州 225009；2.扬州大学现代农村水利研究院，江苏扬州 225009）

0 引言

【研究意义】水文频率计算是各类水利工程规划和管理的主要依据[1]。其是综合运用数理统计方法，分析水文事件的统计规律，通过参数估计方法推求水文分布函数的参数，根据分布函数推求水文变量设计值的过程[2]。受环境变化的影响，流域径流序列表现出显著的变异特征，改变了原始径流序列的统计参数。对依据水文序列平稳性假设的传统水资源规划和管理带来很多挑战[3]。【研究进展】杜懿等[4]对各时间序列进行变异诊断，分别采用基于跳跃诊断的二次修正法、混合分布法和分解合成法等非一致性水文频率分析方法，计算得到各水文站不同重现期的设计年径流量。马钰其等[5]采用Hurst系数法、Spearman 秩次相关检验和Bayesian 变点分析等方法对径流序列进行变异诊断，然后采用水文序列振动中心重构方法对变异序列进行一致性修正，再对修正后的序列进行水文频率分析，计算不同频率的设计年径流量。鲁帆等[6]采用GAMLSS 模型，研究黄河干流年径流系列的非一致性水文频率计算方法，计算出不同频率的设计年径流量。Liu 等[7]采用去平稳性方法去除潜在驱动因素的非平稳影响，将非平稳年径流序列转化为平稳重构序列。Li 等[8]通过将非平稳序列转化为平稳的机制导向重构序列来解决非一致性水文序列的频率分析问题，计算不同频率的设计值并将其与非一致性水文序列结果相比较。【切入点】径流统计特征值可以直观地反映流域径流量的变化情况，统计特征值是否发生变化关系到水文变量设计值的计算精度，并影响到流域水利工程的安危。以往文献多是基于还原或还现方法对发生变异的年径流量序列进行频率分析，对变异条件下径流（年径流量和年最大洪峰流量）序列统计特征值的时变性研究明显不足，也未能揭示径流序列统计特征值时变性对水文频率分析的影响。

【拟解决的关键问题】本研究旨在揭示径流发生变异后对径流统计特征和频率分析所产生的影响。以年径流量和年最大洪峰流量为研究对象，针对径流统计特征和频率分析，分别采用线性趋势分析法、改进的Mann-Kendall 趋势检验法和启发式分割法进行趋势和突变分析，探索其是否存在显著的时变特征。径流统计特征和频率分析可为流域水资源开发利用和防洪提供依据。另外，年最大洪峰流量比年径流量变化更为剧烈，波动性可能会对一定长度下的径流序列的统计特征和频率分析带来影响。综上所述，本研究将分别从序列长度和序列波动性2 个角度揭示径流变异对统计特征和频率分析的影响。研究结果可为黑河流域上游水资源开发利用提供有力支撑，也可为其他流域水资源规划与管理提供重要参考。

1 材料与方法

1.1 研究区概况与数据

黑河是我国第二大内陆河，源于青海省祁连县,地跨青海、甘肃和内蒙古三省。黑河流域以出山口水文站莺落峡站以上的区域为黑河上游，河道长约303 km，流域面积约为10 万km2，占总流域面积的10%左右，是黑河流域主要的产水区[9]。

本研究以黑河流域莺落峡站为例，选用该站1945—2020 年年径流量和1948—2020 年年最大洪峰流量进行水文频率计算，分析其估计参数和设计值的时间变化趋势。数据来源于黄河水利委员会黑河流域管理局。

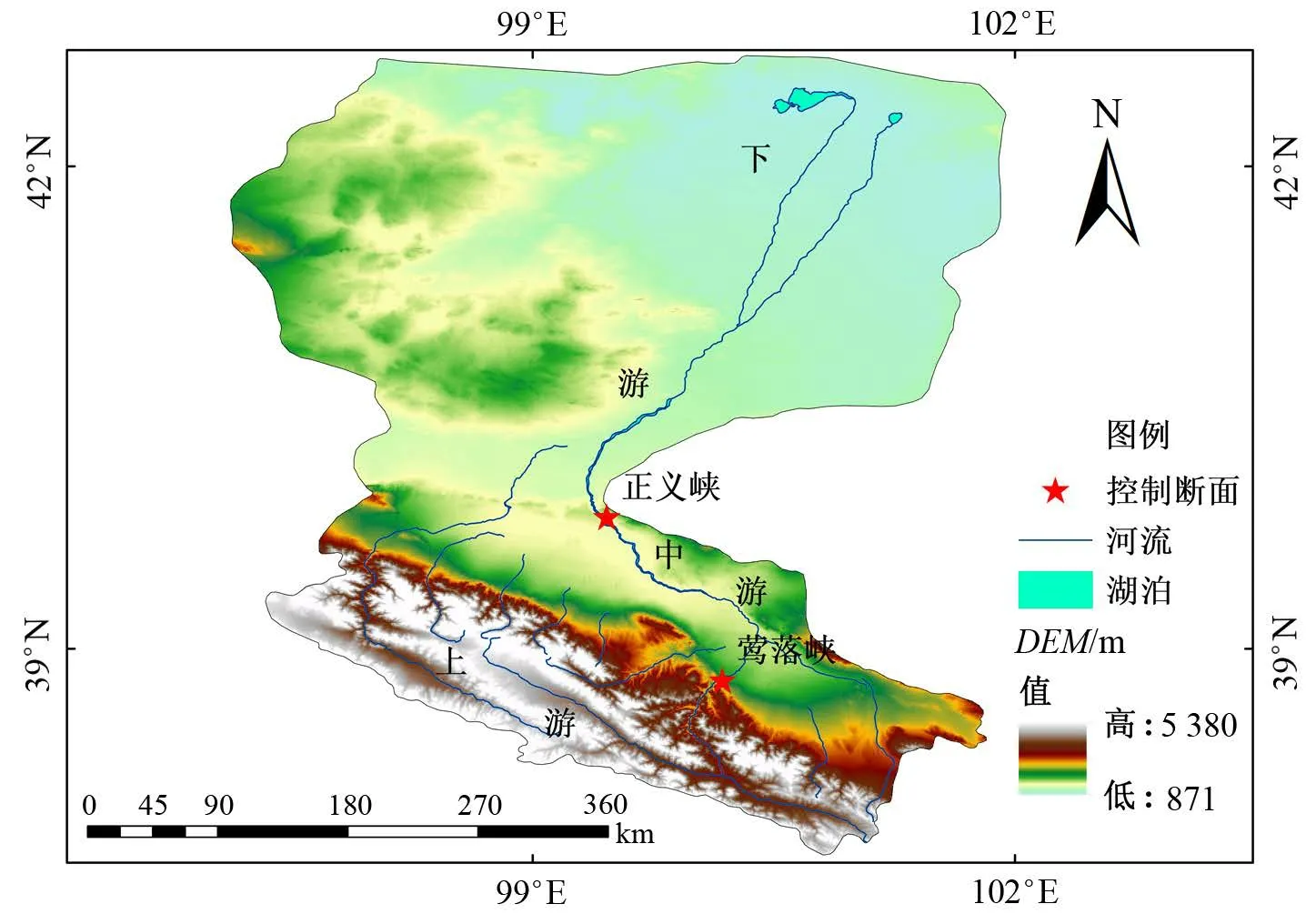
图1 黑河流域高程及水系Fig.1 Elevation and water system of Heihe River basin

1.2 研究方法

1.2.1 滑动窗口分析法[10]

1）定点变宽窗口（A 型窗口）分析

A 型窗口分析主要考察序列长度对径流序列的统计特征和频率分析的影响。对黑河上游1945—2020 年年径流量和1948—2020 年年最大洪峰流量分别采用优化适线法[11]估计其参数和设计值。在数理统计中，30 为大样本容量的经验下限值[12]。以30 a为窗口初始宽度[13]，步长为1 a，从径流序列起始年开始滑动，不断截取A 型窗口序列，并对各窗口序列进行编号。编号规则：1 表示第1 个A 型窗口序列的编号（起止时间分别为1945 年和1974 年），2表示第2 个A 型窗口序列的编号（起止时间分别为1945 年和1975 年），依此类推，可得到47 组年径流量和44 组洪峰流量的A 型窗口序列。

2）变点定宽窗口（B 型窗口）分析

B 型窗口分析重点探究序列波动性对径流序列的统计特征和频率分析的影响。对黑河上游1945—2020 年年径流量和1948—2020 年年最大洪峰流量分别采用优化适线法估计其参数和设计值。保持30 a为窗口宽度，步长为1 a，从径流序列起始年开始滑动，不断截取B 型窗口序列，并对各窗口序列进行编号。编号规则：1 表示第1 个B 型窗口序列的编号（起止时间分别为1945 年和1974 年），2 表示第2 个B 型窗口序列的编号（起止时间分别为1946 年和1975 年），依此类推，可得到47 组年径流量和44 组洪峰流量的B 型窗口序列。

1.2.2 改进的Mann-Kendall 趋势检验法

显著的序列自相关性会影响序列的方差，继而干扰时间序列的趋势检验结果。由于原始的Mann-Kendall 检验法没有考虑序列自相关性的影响[14]，故本研究选用改进的Mann-Kendall 趋势检验法（简称“MMK 检验法”）进行趋势检验。研究表明MMK 检验法在序列存在显著自相关性的情况下是稳健的[15]。

在MMK 检验法中，引入修正系数对原始方差进行修改

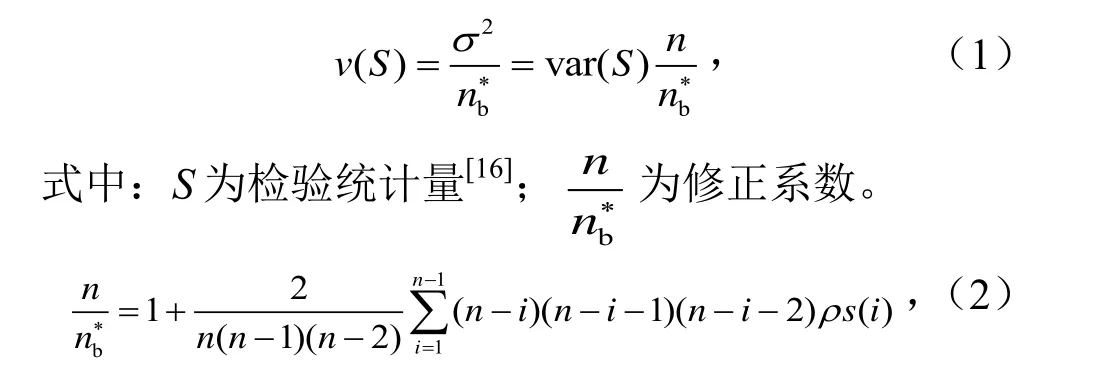
式中：ρS(i)为秩序列的第i阶自相关系数。

Kendall 在1955 年[17]给出计算ρS(i)的方程：

式中：ρ(i)为原始序列第i阶自相关系数。

在式（3）中，ρ(i)为总体自相关系数，可用样本自相关系数ri来估计。样本自相关系数ri的计算公式为：

样本自相关系数ri对总体自相关系数ρ(i)的估计精度随着i的增大而降低[18]。此外，一阶自相关系数（r1）对趋势检验的影响最为突出[19]。因此，本研究在用MMK 检验法对径流序列进行趋势检验时，仅考虑r1的影响。

得到自相关系数r1后，计算其显著性容许限（取显著性水平α=5%）：

式中：取“+”时为容许上限，取“-”时为容许下限。

如果r1位于容许上下限之外，则认为序列的一阶自相关性显著；否则，序列的一阶自相关性不显著，r1=0。

标准化检验统计量：

当|Z|＞Z1-α/2时，表明序列存在显著的趋势；否则，不存在显著的趋势。

1.2.3 启发式分割法

启发式分割法是一种检验非平稳时间序列的有效方法，在医学、水利等相关邻域已有一定的应用[20]。因此，本研究选用启发式分割法进行序列均值突变检验。假设时间序列X(t)的长度为N，从左到右滑动分割点，计算各分割点左右两侧的均值μ1(i)、μ2(i)和标准差S1(i)、S2(i)，分割点的合并偏差表示为：

式中：N1、N2为分割点左右两部分子序列的长度。

采用t检验的统计量T来量化分割点左右两侧均值的差异：

在式（8）中，T越大，表示分割点左右两侧的均值差异越大。确定各分割点中T的最大值Tmax，计算Tmax对应的概率P(Tmax)，即事件T≤Tmax的概率：

在一般情况下，Tmax可以近似表示为：

在式（10）中，由蒙特卡洛模拟可以得到η=4.19lnN-11.54，δ=0.4，V=N-2，lx(a,b)为不完全β函数。

在实际检验中，预设一个临界值P0和序列的最小分割长度l0，若P(Tmax)≥P0且分割的子序列长度大于l0，则在该点处继续分割序列，否则停止分割系列。通过上述操作，P(Tmax)≥P0对应的分割点即为序列均值的突变点。本研究选取P0=0.95，l0=11[21]。

2 结果与分析

2.1 黑河流域上游年径流量时变特征分析1）均值突变检验

采用启发式分割法对不同年径流窗口序列均值突变进行检验，结果如图2 所示（图中红色实线表示统计显著性概率0.95 临界值）。A 型窗口分析中Ex在15 和34 发生突变。Cs在16 和36 发生突变。B 型窗口分析中Ex在32 发生突变，Cν在16 发生突变。

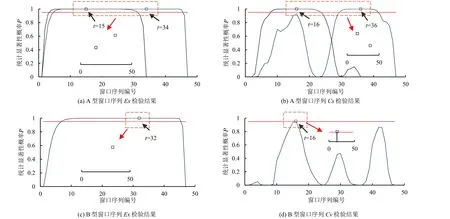
图2 滑动窗口分析法下启发式分割突变检验结果Fig.2 Results of heuristic split mutation test under sliding window analysis method

2）变化趋势分析

采用线性趋势分析法和MMK 检验法对不同年径流窗口序列进行趋势分析，结果如图3 所示。

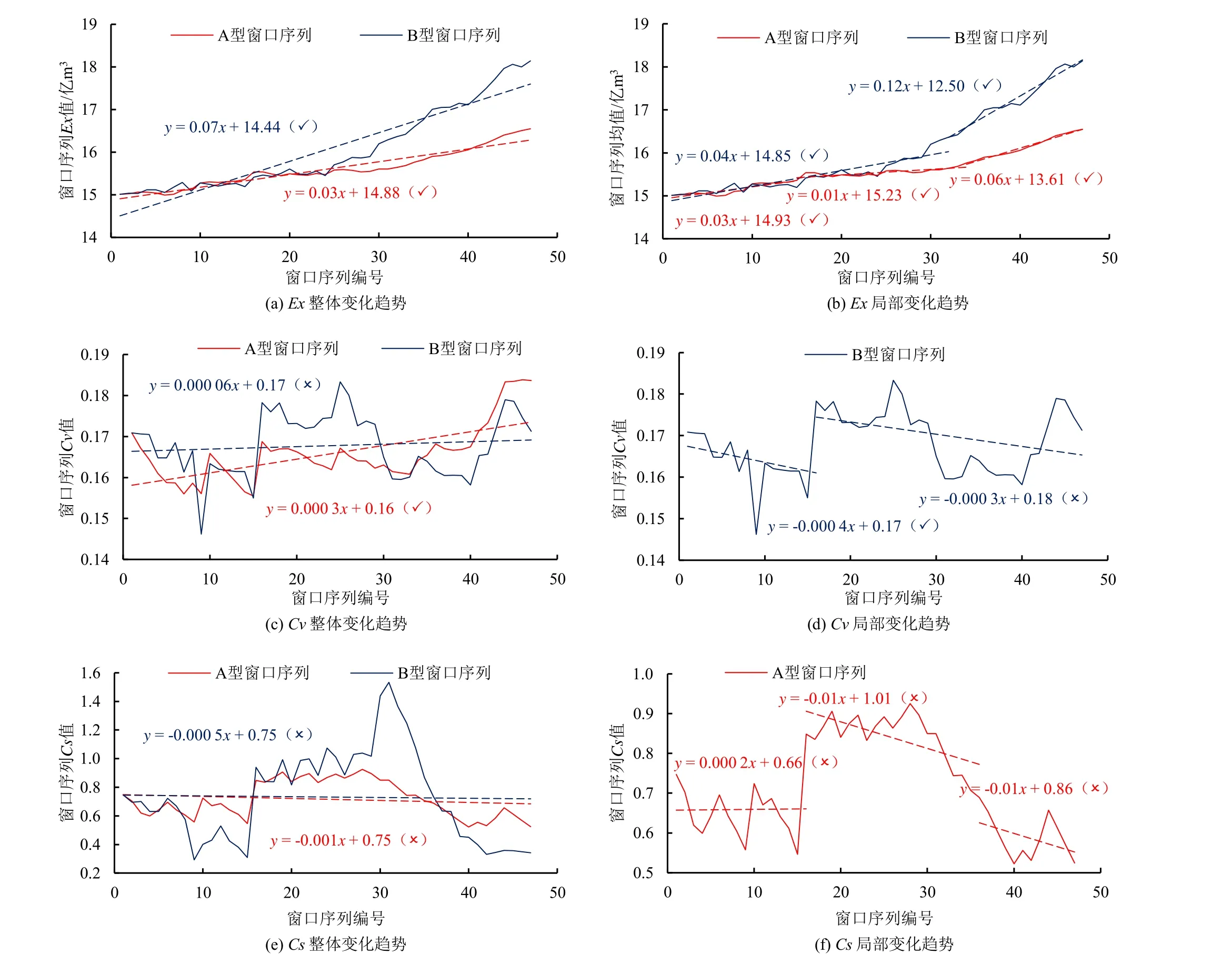
图3 滑动窗口分析法下年径流量估计参数变化趋势Fig.3 Trends in annual runoff estimation parameters under the sliding window analysis method

①整体趋势分析

如图3（a）、图3（c）、图3（e）所示（注：（√）表示Z值超过α=0.05 的显著性水平，（×）表示未超过），A 型窗口分析中，Ex的趋势变化率为0.03（P＜0.01），呈显著的增加趋势（Z=5.83）。Cν的趋势变化率为0.000 3（P＜0.01），呈显著的增加趋势（Z=2.67）。Cs的趋势变化率为-0.001 4（P＞0.01），减小趋势不显著（Z=0.81）。B 型窗口分析中，Ex的趋势变化率为0.07（P＜0.01），呈显著的增加趋势（Z=5.86）。Cν的趋势变化率为0.000 06（P＞0.01），增加趋势不显著（Z=0.81）。Cs的趋势变化率为-0.000 5（P＞0.01），减小趋势不显著（Z=0.16）。

②局部趋势分析

如图3（b）、图3（d）、图3（f）所示，A 型窗口分析中，将Ex分为三段，1～15 的趋势变化率为0.03（P＜0.01），呈显著的增加趋势（Z=3.07）；15～34 的趋势变化率为0.01（P＜0.01），呈显著的增加趋势（Z=3.39）；34～47 的趋势变化率为 0.06（P＜0.01），呈显著的增加趋势（Z=3.99）。将Cs分为三段，1～16 的趋势变化率为0.000 2（P＞0.01），增加趋势不显著（Z=0.74）；16～36 的趋势变化率为-0.01（P＜0.01），减小趋势不显著（Z=1.56）；36～47 的趋势变化率为-0.01（P＞0.01），减小趋势不显著（Z=1.52）。B 型窗口分析中，将Ex分为两段，1～32 的趋势变化率为0.04（P＜0.01），呈显著的增加趋势（Z=4.67）；32～47 的趋势变化率为 0.12（P＜0.01），呈显著的增加趋势（Z=4.03）。将Cν分为两段，1～16 的趋势变化率为-0.000 4（P＞0.01），呈显著的减小趋势（Z=3.05）；16～47 的趋势变化率为-0.000 3（P＞0.01），减小趋势不显著（Z=1.35）。

2.2 黑河流域上游年最大洪峰流量时变特征分析

1）均值突变检验

采用启发式分割法对不同年最大洪峰流量窗口序列均值突变进行检验，结果如图4 所示。A 型窗口分析中Cν和Cs在20 发生突变。B 型窗口分析中Ex在22 发生突变，Cν和Cs在19 发生突变。

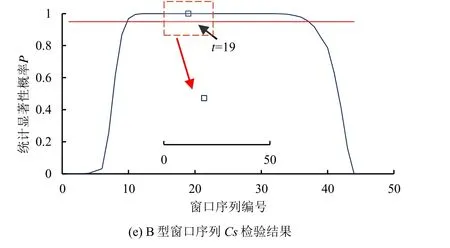
图4 滑动窗口分析法下启发式分割突变检验结果Fig.4 Results of heuristic split mutation test under sliding window analysis method

2）变化趋势分析

采用线性趋势分析法和MMK 检验法对不同年最大洪峰流量窗口序列进行趋势分析，结果如图5所示。

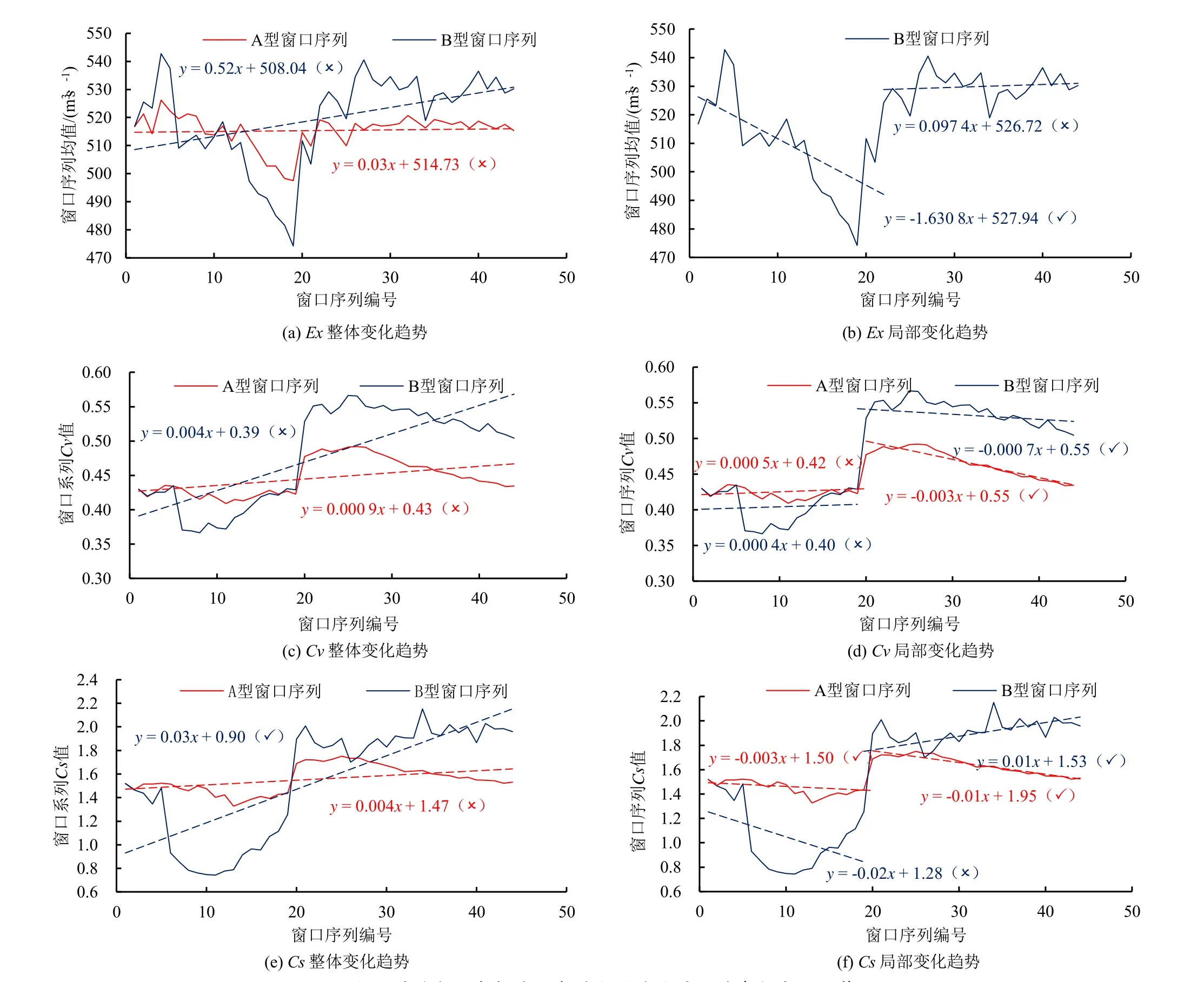
图5 滑动窗口分析法下年最大洪峰流量估计参数变化趋势Fig.5 Trends in estimated parameters of annual maximum flood flow under the sliding window analysis method

①整体趋势分析

如图5（a）、图5（c）、图5（e）所示，A 型窗口分析中Ex的趋势变化率为0.03（P＞0.01），增加趋势不显著（Z=0.06）。Cν的趋势变化率为0.000 9（P＜0.01），增加趋势不显著（Z=1.29）。Cs趋势变化率为0.004（P＜0.01），增加趋势不显著（Z=0.93）。B 型窗口分析中Ex的趋势变化率为0.52（P＜0.01）,增加趋势不显著（Z=1.85）。Cν的趋势变化率为0.004（P＜0.01），增加趋势不显著（Z=1.91）。Cs的趋势变化率为0.03（P＜0.01），呈显著的增加趋势（Z=3.76）。

②局部趋势分析

如图5（b）、图5（d）、图5（f）所示。A 型窗口分析中，将Cν分为两段，1～20 的趋势变化率为0.000 5（P＞0.01），增加趋势不显著（Z=0.37）；20～44 的趋势变化率为-0.003（P＜0.01），呈显著的减小趋势（Z=3.87）。将Cs分为两段，1～20 的趋势变化率为-0.003（P＞0.01），呈显著的减小趋势（Z=2.72）；20～44 的趋势变化率为-0.01（P＜0.01），呈显著的减小趋势（Z=3.84）。B 型窗口分析中，将Ex分为两段，1～22 的趋势变化率为-1.630 8（P＜0.01），呈显著的减小趋势（Z=2.49）；22～44 的趋势变化率为0.097 4（P＞0.01），增加趋势不显著（Z=0.56）。将Cν分为两段，1～19 的趋势变化率为0.000 4（P＞0.01），增加趋势不显著（Z=0.74）；19～44 的趋势变化率为-0.000 7（P＞0.01），呈显著的减小趋势（Z=4.39）。将Cs分为两段，1～19 的趋势变化率为-0.02（P＞0.01），减小趋势不显著（Z=0.71）；19～44 的趋势变化率为0.01（P＜0.01），呈显著的增加趋势（Z=3.81）。

2.3 黑河流域上游年径流量频率分析

1）均值突变检验

采用启发式分割法对不同年径流设计值窗口序列均值突变进行检验，结果如表1 所示。A 型窗口分析中75%频率设计值在11 和32 发生突变。50%频率设计值在10 和35 发生突变。25%频率设计值在14 和35 发生突变。B 型窗口分析中75%频率设计值在31 发生突变。50%和25%频率设计值在34发生突变。

表1 滑动窗口分析法下年径流量设计值启发式分割突变检验结果Table 1 Results of heuristic split mutation test for annual runoff design values under sliding window analysis method

2）变化趋势分析

采用线性趋势分析法和MMK 检验法对不同年径流设计值窗口序列进行趋势分析，结果如图6 所示。

图6 年径流量设计值变化趋势Fig.6 Trends in annual runoff design values

①整体趋势分析

如图6（a）和图6（c）所示，A 型窗口分析中，75%频率设计值的趋势变化率为0.02（P＜0.01），呈显著的增加趋势（Z=5.90）。50%频率设计值的趋势变化率为 0.03（P＜0.01），呈显著的增加趋势（Z=5.81）。25%频率设计值的趋势变化率为0.04（P＜0.01），呈显著的增加趋势（Z=5.38）。B 型窗口分析中，75%频率设计值的趋势变化率为 0.06（P＜0.01），呈显著的增加趋势（Z=5.64）。50%频率设计值的趋势变化率为0.07（P＜0.01），呈显著的增加趋势（Z=5.47）。25%频率设计值的趋势变化率为0.08（P＜0.01），呈显著的增加趋势（Z=5.63）。

②局部趋势分析

如图6（b）和图6（d）所示，A 型窗口分析中，75%频率设计值1～11 的趋势变化率为0.03（P＜0.01），呈显著的增加趋势（Z=3.73）；11～32 的趋势变化率为0.01（P＜0.01），呈显著的增加趋势（Z=3.52）；32～47 的趋势变化率为0.04（P＜0.01），呈显著的增加趋势（Z=4.06）。50%频率设计值1～10 的趋势变化率为0.02（P＜0.01），呈显著的增加趋势（Z=3.12）；10～35 的趋势变化率为0.01（P＜0.01），呈显著的增加趋势（Z=3.96）；35～47 的趋势变化率为 0.07（P＜0.01），呈显著的增加趋势（Z=3.94）。25%频率设计值1～14 的趋势变化率为0.03（P＜0.01），呈显著的增加趋势（Z=2.13）；14～35 的趋势变化率为0.01（P＜0.01），呈显著的增加趋势（Z=2.46）；35～47 的趋势变化率为0.08（P＜0.01），呈显著的增加趋势（Z=3.91）。B 型窗口分析中，75%频率设计值1～31 的趋势变化率为0.03（P＜0.01），呈显著的增加趋势（Z=4.28）；31～47 的趋势变化率为0.10（P＜0.01），呈显著的增加趋势（Z=4.17）。50%频率设计值1～34 的趋势变化率为0.03（P＜0.01），呈显著的增加趋势（Z=4.28）；34～47 的趋势变化率为0.14（P＜0.01），呈显著的增加趋势（Z=3.83）。25%频率设计值1～34 的趋势变化率为0.04（P＜0.01），呈显著的增加趋势（Z=4.61）；34～47 的趋势变化率为0.16（P＜0.01），呈显著的增加趋势（Z=3.60）。

2.4 黑河流域上游年最大洪峰流量频率分析

1）均值突变检验

采用启发式分割法对不同年最大洪峰流量设计值窗口序列均值突变进行检验，结果如表2 所示。年最大洪峰流量不同频率设计值都在20 发生突变。

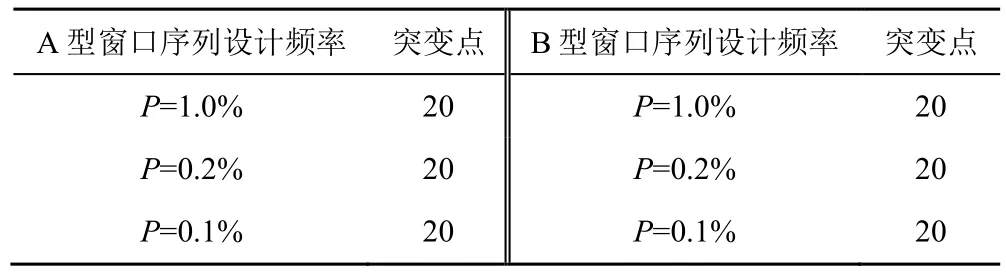
表2 滑动窗口分析法下年最大洪峰流量设计值启发式分割突变检验结果Table 2 Results of heuristic split mutation test for annual maximum flood flow design values under sliding window analysis method

2）变化趋势分析

采用线性趋势分析法和MMK 检验法对不同窗口序列进行趋势分析，结果如图7 所示。

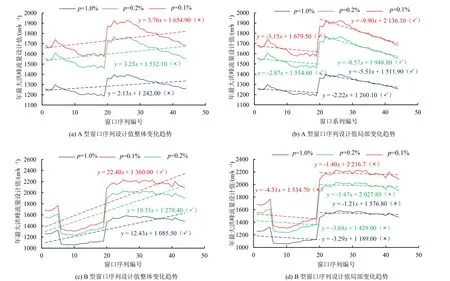
图7 年最大洪峰流量设计值变化趋势Fig.7 Trend of design value of annual maximum flood flow

①整体趋势分析

如图7（a）和图7（c）所示，A 型窗口分析中1%频率设计值的趋势变化率为2.13（P＜0.01），增加趋势不显著（Z=0.54）。0.2%频率设计值的趋势变化率为3.25（P＜0.01），增加趋势不显著（Z=0.57）。0.1%频率的设计值增加速率为3.76（P＜0.01），增加趋势不显著（Z=0.58）。B 型窗口分析中1%频率设计值的趋势变化率为12.43（P＜0.01），呈显著的增加趋势（Z=2.49）。0.2%频率设计值的趋势变化率为19.33（P＜0.01），呈显著的增加趋势（Z=2.66）。0.1%频率的设计值的趋势变化率为22.40（P＜0.01），呈显著的增加趋势（Z=2.75）。

②局部变化趋势

如图7（b）和图7（d）所示，A 型窗口分析中，1%频率设计值1～20 的趋势变化率为-2.22（P＞0.01），呈显著的减小趋势（Z=3.83）；20～44 的趋势变化率为-5.51（P＜0.01），呈显著的减小趋势（Z=4.07）。0.2%频率设计值 1～20 的趋势变化率为-2.87（P＞0.01），呈显著的减小趋势（Z=3.75）；20～44 的趋势变化率为-8.57（P＜0.01），呈显著的减小趋势（Z=4.02）。0.1%频率设计值1～20 的趋势变化率为-3.15（P＞0.01），呈显著的减小趋势（Z=3.61）；20～44 的趋势变化率为-9.90（P＜0.01），呈显著的减小趋势（Z=4.05）。B 型窗口分析中，1%频率设计值1～20 的趋势变化率为-3.29（P＞0.01），减小趋势不显著（Z=0.68）；20～44 的趋势变化率为-1.21（P＞0.01），减小趋势不显著（Z=1.72）。0.2%频率设计值1～20 的趋势变化率为-3.68（P＞0.01），减小趋势不显著（Z=0.56）；20～44 的趋势变化率为-1.47（P＞0.01），减小趋势不显著（Z=1.22）。0.1%频率设计值1～20 的趋势变化率为-4.31（P＞0.01），减小趋势不显著（Z=0.56）；20～44 的趋势变化率为-1.40（P＞0.01），减小趋势不显著（Z=1.00）。

2.5 滑动窗口分析法对比分析

对2 种窗口分析法的P-Ⅲ型曲线拟合度进行比较，结果如表3 和图8 所示。

表3 滑动窗口分析法均值标准差对比分析结果Table 3 Sliding window analysis method mean standard deviation comparison analysis results

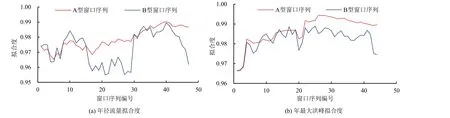
图8 滑动窗口分析法拟合度对比示意图Fig.8 Comparison of the fit of the sliding window analysis

由表3 可知，A 型窗口分析中年径流量拟合度均值和标准差分别为0.980 0 和0.005 0，年最大洪峰流量均值和标准差分别为0.990 0 和0.005 4。B型窗口分析中年径流量拟合度均值和标准差分别为0.970 0 和0.010 0，年最大洪峰流量均值和标准差分别为0.980 0 和0.005 5。由图8 可以看出，A 型窗口分析的拟合度要比B 型窗口分析的拟合度要更稳定，波动程度更小。因此，相比B 型窗口分析，A 型窗口分析有利于进行水文频率计算，可以得到更可靠的径流设计值。

3 讨论

径流统计特征和频率分析可以直观地反映出流域径流的变化趋势，是流域水利工程规划建设的重要指标[22]。受环境变化的影响，黑河流域上游径流表现出明显的变异特征[23]，在变异条件下，统计特征值和设计值必然会受到不同程度的影响。本研究分别采用线性趋势分析法、MMK 检验法和启发式分割法对黑河流域上游径流统计特征值进行趋势和突变检验，用A 型窗口分析和B 型窗口分析2 种不同的角度去探索黑河流域径流统计特征和频率分析的变化趋势，有助于研究区水资源的合理配置和规划管理。

在A 型窗口分析中，年径流量窗口序列随着序列长度的不断增长，估计参数Ex呈现出显著的增加趋势，表示黑河流域上游年径流量发生了显著的变化趋势，这与李培都等[24]和郭巧玲等[23]的研究结果相互验证。估计参数Cν也呈显著的增加趋势，其呈现出由高到低，再由低到高似抛物线型的变化趋势。估计参数Cs存在减小趋势但不明显，由于径流影响因素较多，所以呈现出较为平稳的变化趋势，这些变化趋势与金光炎[25]的研究结果相一致。估计参数Ex决定了水文频率曲线的上下位置，Cν决定了水文频率曲线的形状，Cν值越大，曲线越陡峭[18]。根据年径流量估计参数Ex和Cν的显著的增加趋势，可以得出不同频率的年径流量设计值也相应地存在显著的增加趋势。年最大洪峰流量窗口序列随着序列长度的不断增长，估计参数Ex、Cν和Cs都没有显著的变化趋势，导致不同频率的年最大洪峰流量设计值也不存在显著的变化趋势。

在B 型窗口分析中，窗口序列保持着最小样本长度30 a 序列长度进行分析，年径流量估计参数Ex呈现出显著的增加趋势，Cν和Cs呈现出参差不齐的变化趋势，存在一定的波动情况。由于估计参数Ex的显著增长趋势，提高了水文频率曲线的位置，也可以得出不同频率的年径流量设计值呈现出显著的增加趋势。年最大洪峰流量的估计参数Cs呈现出显著的增加趋势，Ex和Cν不存在显著的变化趋势，但年最大洪峰流量估计参数波动性要比年径流量估计参数更加剧烈，经分析可得年最大洪峰流量估计参数的波动性受极值影响，导致B 型窗口分析比A型窗口分析波动更大。年最大洪峰流量不同频率的设计值呈现出显著的增加趋势，分析原因可得，估计参数Cs决定了水文频率曲线的形状。当Cs越大时，曲线左部越陡，右部越平。年最大洪峰流量设计值的频率都选在曲线最左部分（1%，0.1%，0.2%），受估计参数Cs显著的增长趋势影响，年最大洪峰流量不同频率的设计值也都呈现出显著的增长趋势。

对A 型和B 型2 种窗口分析方法的P-Ⅲ型曲线的拟合程度进行比较，A 型窗口分析的径流设计值拟合度要优于B 型窗口分析的径流设计值拟合度，这与尚晓三等[26]和熊立华等[27]的研究结果一致。在径流过程发生变异的条件下，径流统计特征值和设计值受到径流变异的影响，部分径流统计特征值和设计值呈现出显著的增加趋势且波动性剧烈，由结果分析可得，序列长度的增加可以有效地削弱径流序列波动性的影响，增加设计值的可靠性。随着未来窗口序列的不断加入，黑河流域上游径流量可能会受到气候变化和人类活动等诸多因素的影响，从而导致径流量产生新的变化趋势和突变现象。影响因子的变化会引起径流量怎样的变化，又在径流量变化中起到多大的作用，均需要在后续研究中进一步探索。