基于Richards 模型研究不同水氮水平对向日葵干物质积累与产量的影响
2023-08-09张婷婷梁俊梅
吴 胜,段 玉,张婷婷,安 昊,张 君,梁俊梅,张 胜*
(1.内蒙古农业大学 农学院,呼和浩特 010019;2.内蒙古自治区农牧业科学院 资源环境与可持续发展研究所,呼和浩特 010031)
0 引 言
【研究意义】作物的产量形成依托于地上部的干物质积累,其经济系数常常稳定在一定范围,因此干物质积累越大,往往产量越高。随着信息技术的发展,作物模型得到了越来越多的研究与应用。通过模型模拟,可以量化分析,从而使对作物生长规律的定性描述转向定量分析[1]。作物模型可以分为机理性模型和经验性模型。前者从生长机理出发,而后者往往不考虑行为的机理过程,多由一个或多个数学方程组成,这类模型操作简单,针对性和应用性强[2]。应用此类经验性模型便可以定量分析作物的生长动态过程。【研究进展】常常用于描述干物质积累的模型有Logistic 模型[3]和Richards 模型[4]。Logistic 模型最早在研究作物干物质积累过程与气象条件的关系时被引入[5-6],此后在水稻、小麦和玉米等作物的干物质动态分析中多有应用[7-9]。但有学者指出Richards 模型相较Logistic 模型更适合描述作物的生长动态过程[10-11],因为多了一个参数的Richards 模型可塑性更强,不再局限于变化曲线是围绕增长速率最大点的点对称图形。因此,越来越多的学者用Richards 模型去模拟分析作物的生长过程[12-15]。
水分和氮肥往往是作物生长的最主要限制因素,在干旱区和半干旱区更是如此。武川地处北方农牧交错带,该区域降水量低,以典型的旱地农业为主[16],这里水资源短缺,农业用水全靠开采地下水,过度开采地下水会给生态带来一系列问题。氮素是向日葵叶绿素的重要构成元素,通过施用氮肥可以补充土壤可利用氮,进而促进向日葵生长。但过量施氮会污染地下水、土壤和空气[17]。在作物生产过程中,水分的亏缺会影响氮肥的吸收,缺少氮肥又影响植株的发育,这又反过来影响作物对土壤水分的利用[18-19]。作物的地上部干物质积累过程与产量形成密切联系,通过模型拟合便可对不同水氮处理的向日葵地上部干物质积累进行动态分析,进而弄清水分和氮肥是如何影响向日葵的生长。运用Richards 模型模拟不同水氮处理对向日葵地上部干物质积累过程以及利用方程关键生长参数分析干物质积累和产量的关系尚未见报道。【切入点】本研究通过在北方农牧交错带内蒙古阴山北麓自治区农牧业科学院武川试验站进行不同灌水、施氮水平的田间试验,运用Richards 模型模拟地上部干物质积累和向日葵生长有效积温(GDD)的关系,并对地上部干物质积累的生长参数进行定量分析,探究灌水施氮对向日葵地上部干物质积累过程的调控以及对产量的影响。【拟解决的关键问题】以此确定施氮和灌水对地上部干物质积累的调控作用和干物质积累对产量形成的影响作用,为当地的食葵种植提出高产节水节肥的水氮调控策略。
1 材料与方法
1.1 试验区概况
试验于2021 年在北方农牧交错带内蒙古阴山北麓自治区农牧业科学院武川试验站进行,土壤为栗钙土,质地为壤土,0~20 cm 土壤粒径占比分别为:>2 mm 占8.77%,0.25~2 mm 占9.54%,0.053~0.25 mm 占9.71%,<0.053 mm 占13.43%。试验前采样并测定得到土壤数据:pH 值为7.9,有机质量9.6 g/kg,硝态氮量7.5 mg/kg、铵态氮量3.8 mg/kg,有效磷量11.4 mg/kg,速效钾量65 mg/kg,阳离子变换量CEC16 cmol/kg。试验材料为食用向日葵龙葵27。播种为5月7 日,收获期为9 月29 日。
1.2 试验设计
试验采用裂区设计,各处理重复3 次,小区面积36 m2(7.5 m×4.8 m),基于大垄双行覆膜滴灌的栽培模式,大垄间距120 cm,小垄间距40 cm,向日葵株距60 cm。本试验共设有9 个处理,包含主、副因素,各3 个水平,主因素为3 个灌溉模式:不灌雨养W0(覆膜种植,播后保苗水300 m3/hm2)、补水灌溉W1(覆膜种植,生育期总灌水量为900 m3/hm2,播后保苗水300 m3/hm2,苗期300 m3/hm2,现蕾期300 m3/hm2)和正常灌溉W2(覆膜种植,生育期总灌水量为1 500 m3/hm2,播后保苗水300 m3/hm2,苗期300 m3/hm2,现蕾期300 m3/hm2,花期300 m3/hm2,灌浆期300 m3/hm2)。副因素为3 个施氮水平:0、135 kg/hm2和270 kg/hm2,表示为N0、NE 和NF。其中NE 135 kg/hm2是根据向日葵养分专家系统确定的[20]。其中氮肥用尿素(有效氮量为46%),30%基施,70%追施(分别在7 月10 日、7 月24 日、8 月7日随滴灌施入);磷肥和钾肥施用量按照养分专家系统推荐用量分别为70 kg/hm2和120 kg/hm2,其中磷肥全部作为基肥施用,钾肥的1/2 作为种肥基肥,1/2追施(分别在7 月10 日、7 月24 日、8 月7 日、8月28 日随滴灌施入)。生育期降水量如表1 所示。

表1 生育期降水量Table 1 Precipitation during the growing period
1.3 测定项目与方法
1)干物质积累(DMA)
在向日葵苗期标记长势一致的向日葵20 株,分别于向日葵苗期、现蕾期、开花期、灌浆前期、灌浆后期、成熟期取3 株已标记植株,在晾晒后,于85 ℃烘干至恒质量,测定干物质量。
2)籽粒产量
收获时,取试验小区中间两大垄收获测产。
3)有效积温(GDD)
根据农牧业科学院武川试验站小型气象站测得的气温数据计算出向日葵生长的有效积温,计算式[21]如下:
式中:i为向日葵播种后的第i天;GDDi为向日葵播后至第i天的有效积温;DATi为第i天的有效积温;Tmaxi和Tmini为气象站测得第i天的最高气温和最低气温;Tb为向日葵生长的最低温度。本试验将Tb设为10 ℃。
1.4 Richards 模型及有效性检验
1.4.1 Richards 模型及特征参数
Richards 方程曲线近似S 型,如式(3)所示。本试验以向日葵地上部干物质积累量为因变量Y,以向日葵生长有效积温为自变量x,其中,A为终极生长量,b为初值参数,c为生长速率参数,N为形状参数,具体方程如式(3)所示[21]:
对Richards 方程求导得到向日葵地上部干物质积累速率随积温变化的方程,具体方程如式(4)所示:
对方程(4)求导得到向日葵地上部干物质积累速率的瞬时变化率随积温变化的方程,具体方程如式(5)所示:
令向日葵地上部干物质积累速率的瞬时变化率为0 可求得干物质积累速率最大时的有效积温xmax,见式(6):
将xmax代入(5)式可以计算出向日葵地上部干物质积累的最大速率Vmax,见式(7):
将xmax代入(4)式可以计算出向日葵地上部干物质积累速率最大时的干物质积累量YVmax及YVmax所占向日葵地上部干物质积累的理论最大值A的百分比I,见式(8)—式(9):
对式(5)在0 到A上积分再平均即可得到DMA的平均生长速率Vavg[22]:
对方程(5)求导后使其等于0,可以计算得到2 个积温值x1和x2,见式(11)、式(12):
将积温x1和x2分别代入方程(5)可以得到向日葵地上部干物质积累速率的瞬时变化率的最大值与最小值,并以此将向日葵地上部干物质累积过程分为渐增期、快增期和缓增期,即[0,x1]是渐增期,[x1,x2]是快增期,[x2,GDDm]是缓增期,GDDm为播后至收获时的有效积温。令x2与x1相减得到快增期的有效积温Δx,见式(13):
将x1代入式(3)得到渐增期向日葵干物质积累量y1,将x2和x1分别代入式(3)并令其相减得到快增期向日葵干物质积累量y2,将GDDm和x2分别代入式(3)并令其相减得到缓增期向日葵干物质积累量y3。
用快增期干物质积累量y2除生育期总干物质积累量(y1+y2+y3)得到快增期干物质积累量占总干物质积累量的比例z。
1.4.2 模型有效性检验
用决定系数(coefficient of determination,R2)、标准化的均方根误差(normalized RMSE,nRMSE)和平均绝对误差(average absolute error,AAE)对方程的拟合效果进行评估,其计算式为[23]:

1.5 数据统计分析
本研究采用Curve Expert Professional 软件对向日葵地上部干物质积累量和有效积温的关系进行拟合并得到方程曲线参数。应用matlab 2019 对Richards方程进行求导。灌水、施氮对地上部干物质积累特征值的影响用SAS9.4 进行方差分析,多重比较应用LSD(leastsignificant difference)法。逐步回归用DPS数据处理软件完成。
2 结果与分析
2.1 模型拟合情况
方程的拟合情况见图1,9 张子图中的圆圈分别为不同处理下的地上部干物质积累量的实测值,其越接近曲线表明方程的拟合效果越好,各水氮组合条件下拟合曲线的参数及决定系数见表2。各个不同处理下方程的决定系数均大于0.984,表明此模型可以较好地描述向日葵地上部干物质的积累过程。对不同水氮处理下拟合方程的参数进行方差分析,结果见表2。通过F测验可以发现灌水对曲线参数A、c有极显著影响,对b有显著影响,施氮量对A、b、c有极显著影响,对氮有显著影响。
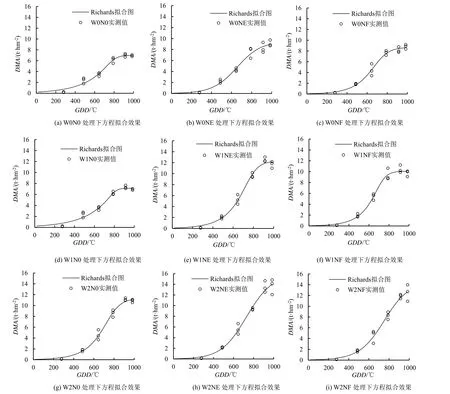
图1 各水氮处理Richards 方程拟合情况Fig.1 Fitting of Richards equation for each water and nitrogen treatment
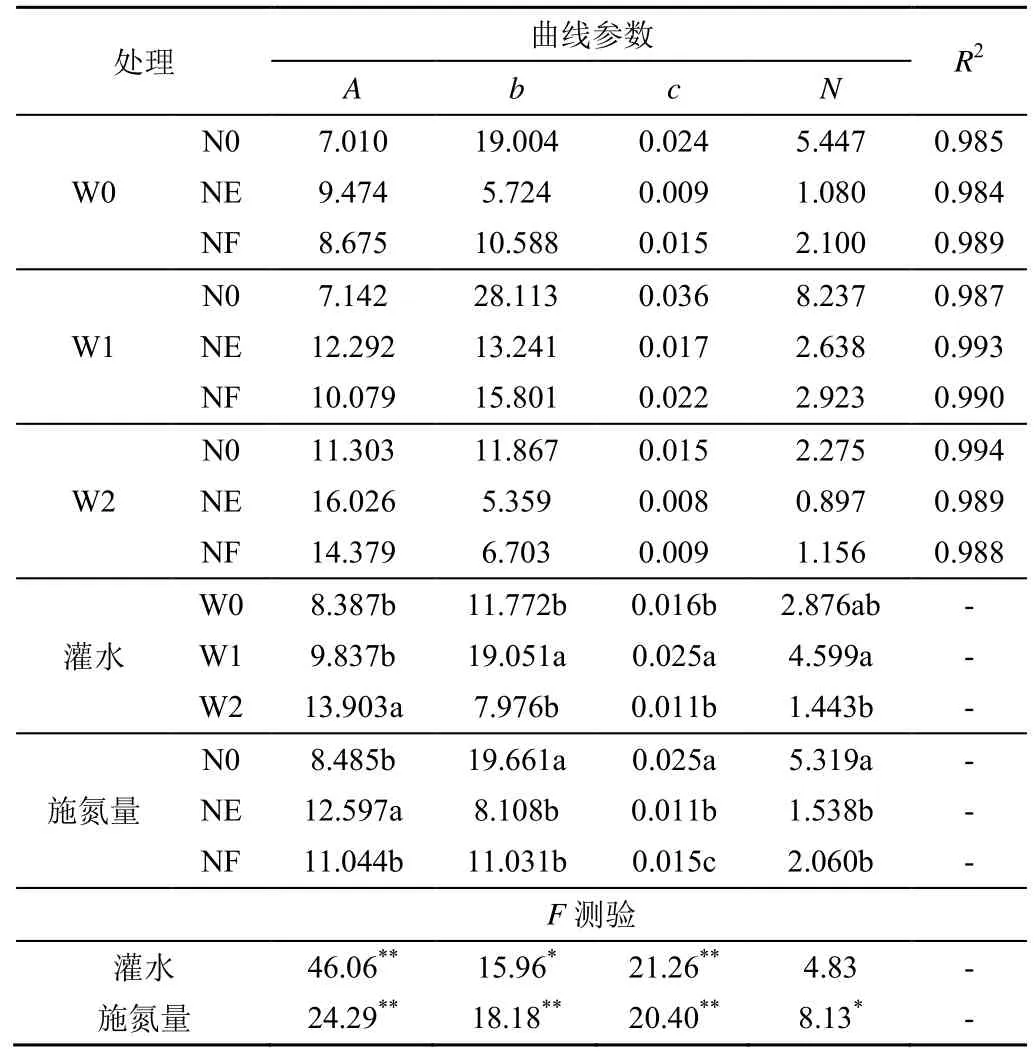
表2 向日葵DMA 动态变化过程的Richards 模型曲线参数Table 2 The curve parameters of the Richards model for the dynamic change process of sunflower DMA
为了检验模型的模拟效果,将生育期内取样测得的向日葵地上部干物质量与方程的模拟值作对比,在此随机选取W1NE、W2N0、W0NF 处理。具体模拟效果见图2,图中直线均为y=x,直线上方的点表明模型模拟值大于实际值,下方的点表明模型模拟值小于实际值,点越靠近直线说明模拟值与实际值越接近。经过模型有效性检验,随机选取3 个处理的模拟方程的决定系数均大于0.989,标准化的均方根误差分别为8.28%、7.52%、9.52%,方程的模拟效果优秀,并且其余各处理模拟方程的决定系数均大于0.98,平均绝对误差均小于0.6,标准化的均方根误差均小于12%,说明Richards 模型对不同水氮条件下向日葵地上部干物质积累的模拟效果都很好,并且由模型进一步推导出来的干物质积累特征参数更有实际意义。
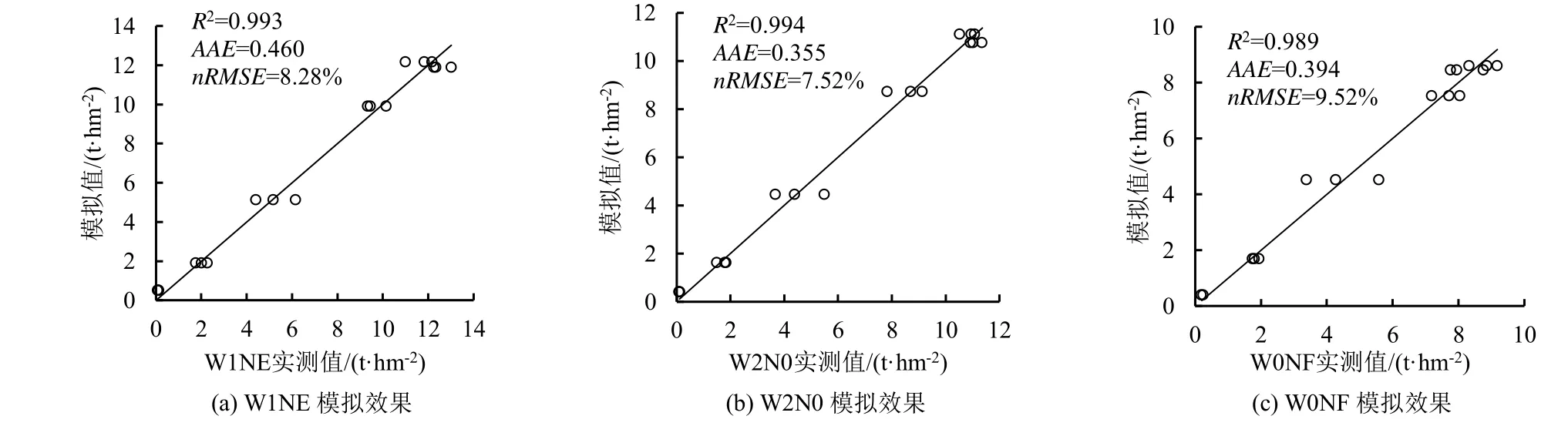
图2 向日葵DMA 动态积累的实测值与模拟值Fig.2 Measured and simulated values of DMA dynamic accumulation in sunflower
2.2 不同水氮处理对向日葵地上部干物质积累的影响
对不同水氮处理下拟合方程的特征参数进行方差分析,结果见表3。由F测验可以看出不同的灌水对I(干物质积累速率最大时的干物质积累量占总干物质积累量的比例)、y2(快增期干物质积累量)和z(快增期干物质积累量占总干物质积累量的比例)有极显著影响,对YVmax(物质积累速率最大时的干物质积累量)、Δx(快增期持续时间)和y1(渐增期干物质积累量)有显著影响。而不同施氮水平对I(干物质积累速率最大时的干物质积累量占总干物质积累量的比例)、y2(快增期干物质积累量)和z(快增期干物质积累量占总干物质积累量的比例)有极显著影响,对Δx(快增期持续时间)有显著影响。表明灌水、施氮主要通过对向日葵从播种后到干物质积累速率达到峰值以及干物质积累快增期这2 个阶段的影响来达到对干物质积累的调控。
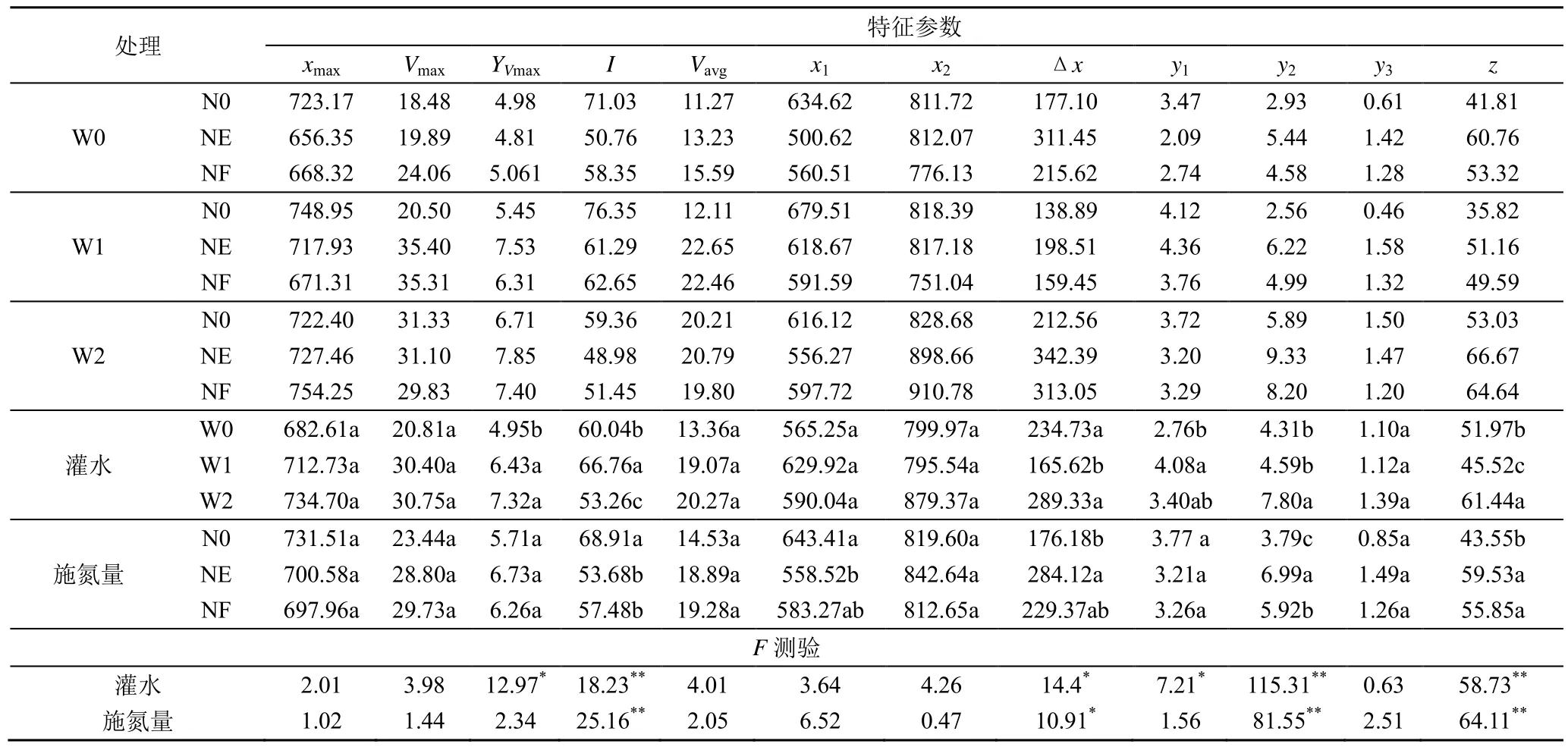
表3 DMA 特征参数Table 3 DMA characteristic parameters
2.2.1 不同灌水对向日葵地上部干物质积累的影响
不同灌水处理的向日葵地上部干物质积累速率变化见图3,特征参数见表3。从向日葵播种后到干物质积累速率达到峰值这一阶段,补水灌溉和正常灌溉的干物质量显著高于雨养模式,说明灌水在较早的阶段就已经开始影响干物质积累,但是补水灌溉I较雨养模式显著提高,而正常灌溉I较雨养模式显著降低则说明了更高的灌溉水平使向日葵干物质积累速率达到峰值后仍能表现出较好的干物质积累水平,这是因为正常灌溉在花期和灌浆期分别进行了灌水。
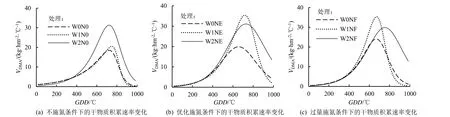
图3 DMA 速率动态变化Fig.3 DMA rate dynamic change
相较于雨养模式,补水灌溉的快增期持续时间显著降低,而正常灌溉有些许提高,这是由于补水灌溉和正常灌溉更晚进入快增期的同时,补水灌溉却和雨养模式几乎同时结束快增期,而正常灌溉的快增期结束时间则更晚,快增期持续时间更长。补水灌溉在苗期和现蕾期给予适当的灌水使向日葵在花前达到较大的干物质积累量,而在花后始终不灌与较大干物质积累量所对应的需水量并不匹配,从而使向日葵在花后始终处于水分亏缺状态,也因此干物质积累速率急速下降,更早的结束快增期,而进入缓增期。
快增期干物质积累量与快增期持续时间和快增期积累速率这2 个因素有关,由于快增期持续时间和积累速率均较大,正常灌溉的快增期干物质积累量显著高于雨养模式和补水灌溉,因此正常灌溉的快增期干物质积累量占比显著高于雨养模式和补水灌溉。此外补水灌溉的快增期干物质积累量占比显著低于雨养模式,这是因为补水灌溉和正常灌溉所分别对应的快增期干物质积累量和缓增期干物质积累量基本没有差异的情况下,补水灌溉的快增期干物质积累量较雨养模式显著提高,这也是由于在渐增期补水灌溉积累速率大于雨养模式,从而积累了较多的干物质。
2.2.2 不同施氮对向日葵地上部干物质积累的影响
不同施氮处理的向日葵地上部干物质积累速率变化见图3,特征参数见表3。优化施氮、过量施氮的YVmax较不施氮稍有增加,但I却显著降低,这说明氮肥在干物质积累速率达到峰值之前影响不大,主要在峰值之后产生作用。
与灌水的作用相反,施氮使向日葵提早进入快增期,图3(b)和图3(c)(施氮处理)的曲线峰值出现时间早于图3(a)(不施氮处理)。进而也使快增期所持续的时间较不施氮有了显著的提高。另一方面,优化施氮快增期持续时间较不施氮和过量施氮分别增加了61.27%和23.87%,这说明过度的施氮反而会引起快增期持续时间减小。氮肥对快增期干物质积累量的影响与快增期持续时间一致,优化施氮的快增期干物质积累量较不施氮和过量施氮分别提高了84.55%(P<0.05)和18.12%(P<0.05)。这也是因为在干物质积累速度基本一致的情况下,优化施氮的快增期持续时间较过量施氮更长。
此外,施氮相较不施氮提高了干物质积累的最大速率,但干物质积累的最大速率不会因为施氮量的增多而产生线性的增长。
2.3 不同水氮梯度的向日葵干物质积累过程对产量的影响
2.3.1 相关分析
计算12 个DMA特征值xmax(X1)、Vmax(X2)、YVmax(X3)、I%(X4)、Vavg(X5)、x1(X6)、x2(X7)、Δx(X8)、y1(X9)、y2(X10)、y3(X11)、Y%(X12)及产量之间的相关系数,得相关系数矩阵,如表4 所示。除I(干物质积累速率最大时的干物质积累量占总干物质积累量的比例)和x1(渐增期持续时间)以外,其余各特征值均与产量正相关。其中产量和YVmax(r=0.894 5)、Vavg(r=0.840 7)、y2(r=0.955 2)、z(r=0.806 8)达到极显著正相关,与Vmax(r=0.779 6)和y3(r=0.752 1)达到显著正相关。说明在一定范围内提升快增期干物质积累量、干物质积累速率最大时的积累量、干物质积累平均速率、干物质积累速率最大时的积累量占比、最大干物质积累速率和缓增期干物质积累量均可显著提高产量。
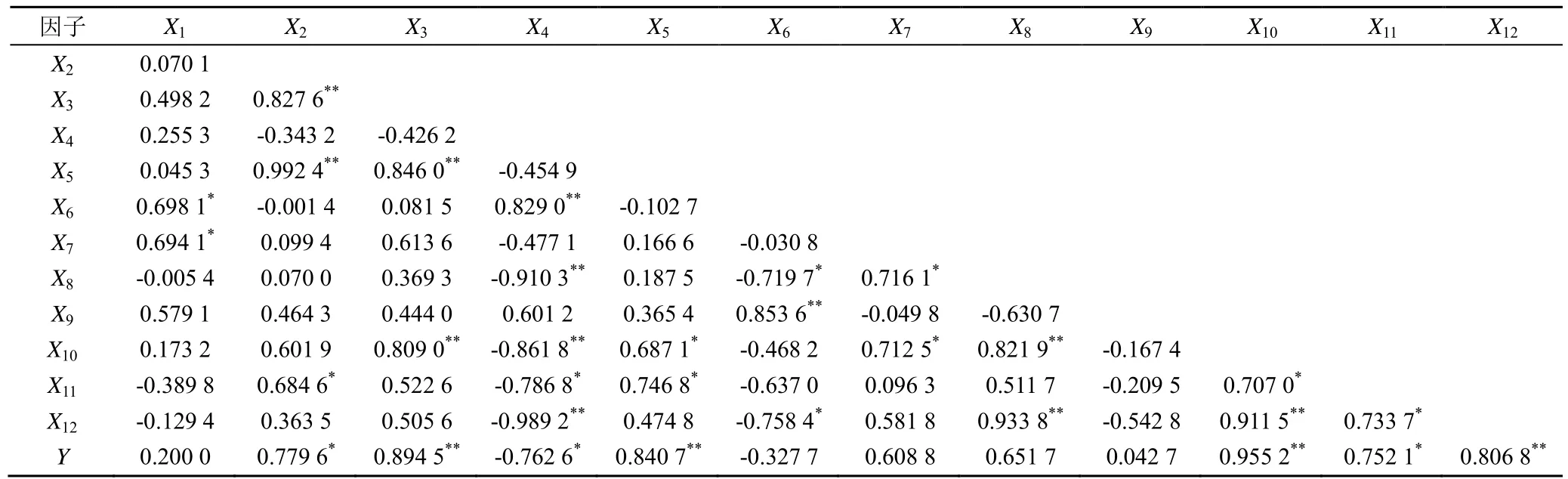
表4 DMA 特征值及产量之间的相关关系矩阵Table 4 Correlation matrix between DMA eigenvalues and yield
从性状之间的相关分析来看,YVmax(物质积累速率最大时的干物质积累量)和快增期干物质积累量极显著正相关(r=0.809 0),表明自快增期开始到干物质积累速率达到峰值这段时间的干物质积累在整个快增期的占比较大,二者共同促进产量的提升。快增期干物质积累量和快增期持续时间极显著正相关(r=0.821 9),说明延长向日葵快增期的时间可以显著增加快增期干物质积累量。最大干物质积累速率和缓增期干物质积累量显著正相关(r=0.684 6),表明生育前期拥有旺盛的生长将促进缓增期的干物质积累,并且二者又共同促进产量的提升。
2.3.2 多元线性回归分析
为了确定各个干物质积累特征值对产量的各自效应和综合效应,以便抓住关键的干物质积累特征值,能动的调控产量的响应量,对各特征值与产量进行多元回归分析。
通过逐步回归,经过9 次剔除,每次淘汰一个偏回归平方和最小且未达到极显著水平的自变量,最终获得的最优线性回归方程为:y=272.209-5.450X1+49.370X2+7.376X7,复相关系数为 0.994 6,F=153.19**,表明xmax(X1)、Vmax(X2)、x2(X7)与产量(y)存在着极显著的线性回归关系,且xmax(X1)、Vmax(X2)和x2(X7)与产量(y)的偏回归系数也均达到了极显著,见表5,多元决定系数R2=0.989 2,表明产量的98.92%是由最大干物质积累速率出现时间,最大干物质积累速率和快增期结束时间这3 个干物质积累特征值决定的,剩余因素(误差和其他影响产量的因素)对产量的影响仅为1.08%,因此可以用该回归方程来预测产量。
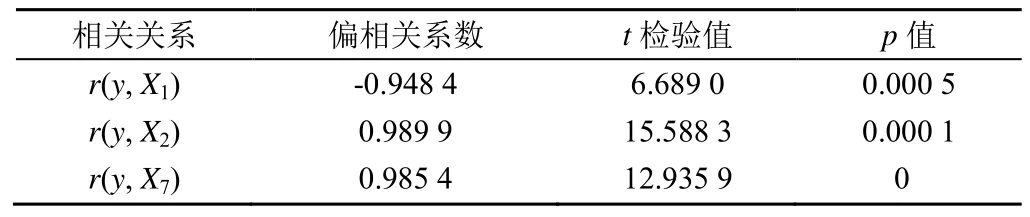
表5 最优线性回归方程的偏相关系数Table 5 Partial correlation coefficient of optimal linear regression equation
2.3.3 回归方程拟合效果检验
为了检验回归方程的拟合效果,将9 个处理的实测值与预测值做对比分析,由图4 可以看出,最优线性回归方程的模拟值与实测值非常接近,决定系数为0.989,标准化的均方根误差为1.16%,方程的模拟效果优秀,说明通过最大干物质积累速率出现时间、最大干物质积累速率和快增期结束时间这3 个因素可以很好地预测与调控产量。
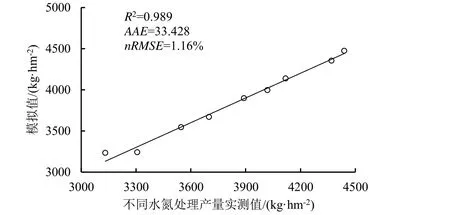
图4 多元回归方程的模拟值和实测值Fig.4 The simulated and measured values of the multiple regression equation
2.3.4 通径分析
最优多元线性回归方程中的偏回归系数表示了干物质积累特征值对产量的具体效应,但实践中还需要评定这些干物质积累特征值的相对重要性,以确定关键因素,达到调整和控制产量响应量的目的。因此进一步进行通径分析,分析结果见表6,xmax(X1)、Vmax(X2)和x2(X7)决定了产量变异的98.92%,3 个干物质积累特征值的直接通径系数大小依次为x2(X7)>Vmax(X2)>xmax(X1),
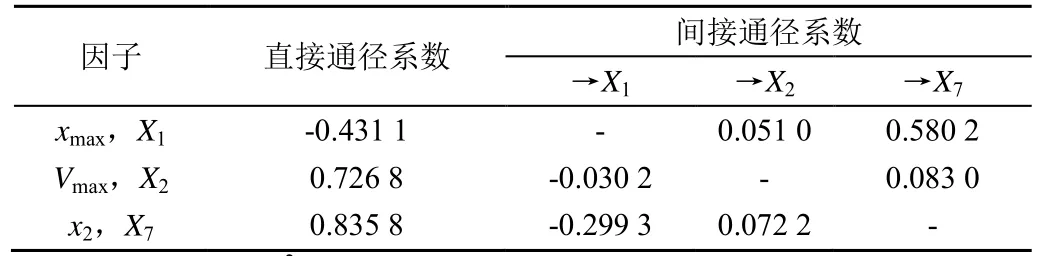
表6 DMA 关键特征值对产量的通径分析Table 6 Path analysis of key eigenvalues of DMA to yield
其中最大干物质积累速率出现时间的直接通径系数为负值,表明在其他干物质积累特征值不变的条件下越早达到最大干物质积累速率,越有利于增产。在各间接通径系数中,xmax(X1)通过x2(X7)对产量有正向效应(P1→7→Y=0.580 2),表明干物质积累速率的峰值延后会使快增期结束的时间延后,进而促进产量增加。Vmax(X2)的2 个间接通径系数均小于0.1,表明Vmax(X2)与xmax(X1),x2(X7)的相关性较低(r12=0.070 1,r27=0.099 4),即最大干物质积累速率受最大干物质积累速率出现时间和快增期结束时间的影响较小。
3 讨 论
3.1 Richards 模型的拟合效果
作物的干物质积累是产量形成的基础,作物经济系数常常稳定在一定范围,因此干物质积累越大,往往产量越高。通过生长函数的拟合便可得到干物质积累的动态增长过程,再经过一系列数据的分析,便能得知干物质增加的内在原因。这种定量的分析过程可以把握到高产群体的关键指标。进而为促产提供方向与目标[24]。有研究表明,Richards 模型较Logistics模型更适合描述作物的S 型生长[25-26]。多数研究利用Richards 模型模拟作物干物质积累的效果均不错,如宋明丹等[21]和张旭等[13]分别利用Richards 模型模拟不同水氮水平的冬小麦地上部干物质积累过程,拟合方程的决定系数分别达到0.980 和0.996 以上。张兵兵等[27]通过对数据进行归一化处理,筛选出最适合模拟不同品种和不同播期春玉米地上部干物质积累的模型为Richards 模型,各个不同处理拟合方程的决定系数均在0.980 以上。本研究拟合结果显示,各水氮条件下Richards 拟合方程的决定系数均在0.984 以上,表明方程可以很好地拟合出向日葵地上部干物质积累的动态变化。
在收获时期,补水灌溉条件下向日葵干物质积累出现了明显的负增长(图1(d)、图1(e)、图1(f)),但是Richards 模型无法拟合出这种情况,当有效积温趋向于无穷大时,干物质积累量只能趋向于A(终极生长量)。当然补水灌溉条件下都出现了这种负增长的情况有很大可能是因为衰老发生的较早且剧烈,以至于叶片过早衰落和凋零,从而产生干物质积累的负增长。
此外,干物质积累的实际生理过程还是较为复杂的,而且受环境生态等各种因素的制约,本研究仅用模型对1 年的向日葵干物质积累进行模拟,模拟效果的稳定性还需要进一步的验证。
3.2 施氮对向日葵地上部干物质积累的影响
干物质的多少决定作物产量的高低[28-29],往往长势好、干物质量高的作物产量高。向日葵在快增期积累的干物质占总干物质1/2 以上,在灌水施氮的处理上占比更高,而且向日葵总干物质量的差异也主要在此阶段形成。氮既是酶、ATP、多种辅酶的组成成分,又是叶绿素的成分,因此,与光合作用密切相关,进而影响着干物质的积累。本研究中施氮显著提高了快增期的持续时间,从而也提高了快增期的干物质积累量,这与张旭等[13]的研究结果一致。施氮处理使向日葵提前进入快增期,这可能是因为生育前期足够的氮肥可以使叶片的光和生产能力提高,干物质积累更多,叶面积也更大,从而更早进入快增期;施氮处理也使快增期的结束时间延后,这大概率是生育后期氮素转移[30]的原因。生育后期营养器官和生殖器官共同竞争碳同化产物和养分,加速了叶片器官中氮素向外转移以及衰老,叶绿体是叶片衰老过程中氮转移的主要来源,Rubisco 与其他光合蛋白一起,在叶片衰老时大量降解,提供籽粒生长过程中需求的氮素[31],但生育后期的充足供氮延缓了此过程,从而使快增期的结束时间延后。
3.3 灌水对向日葵地上部干物质积累的影响
水分是影响作物生长的关键因素之一,在干旱及半干旱地区,补充灌水可以延缓叶片衰老,延长光合作用时间,进而提高地上部干物质的积累量和产量。Villegas 等[32]、赵姣等[33]和张旭等[13]研究认为灌水能缩短达到冬小麦地上部干物质积累最大速率和进入快增期的时间,这与本试验的研究结果相反,本试验结果表明灌水量的增加会延长达到向日葵地上部干物质积累最大速率和进入快增期的时间。分析本试验出现此情况的原因:Richards 方程的三阶导数表达的含义是干物质积累速率的瞬时变化率随积温的变化,其峰值的出现代表进入快增期,在灌水没有出现差异之前,其值是没有出现差异的,当灌水出现差异了,其值开始有不同的发展趋势,具体表现为不灌水给向日葵带来了生理干旱,生长势减小,相比正常灌溉不灌水处理植株较低的生长势使其很快达到积累速率的变化率的峰值(此峰值过后积累速率的增加就没前期那么高了),也就是快增期出现时间较早,而补水灌溉和正常灌溉的灌水使其生长势较高,积累速率变化率达到峰值的时间延长,结果为其二者的快增期时间延后但进入快增期时的积累速率更高。而张旭等[13]试验灌水设置与本试验设置不同,本试验的灌水设置涉及分次灌水,而他的灌水是一直保持恒定的田间持水量,并且试验对象也由冬小麦变成向日葵。
除此之外,灌水对快增期结束时间的调控也值得探讨,相较于不灌水,补水灌溉在基于苗期和现蕾期灌水的条件下,进入快增期的时间延后了,最大干物质积累速率增加了,但是却和不灌水几乎同时离开快增期,正常灌溉的情况与此不同,由于花期和灌浆期有灌水,快增期结束时间显著延后。分析原因可能是补水灌溉在营养生长阶段给予适当的灌水使向日葵在花前达到较大的干物质积累量,而在花后始终不灌与较大干物质积累量所对应的需水量不匹配,从而使向日葵在花后始终处于水分亏缺状态,也因此干物质积累速率急速下降,更早的结束快增期,而进入缓增期。
3.4 从干物质积累角度出发的增产决策
在通径分析中,通过多个自变量与因变量的相关系数的剖分,可以明白各个因子之间的关系,但是很难明确看出哪个干物质积累特征值对产量起着主要决定性作用或主要限制性作用,为此,本研究通过求解各变量的决策系数,以进行综合决策[34]。决策系数反映了某个因素通过所有因素的相关网对y的综合决定作用,它不仅包含了这个因素对因变量的直接决定作用,还包含了与这个因素有关的间接决定系数。决策系数的求解公式为=2biriy-bi2,式中表示因素的直接通径系数,riy表示Xi因素和y的相关系数。求解得到=-0.358 3=0.605 0,)=0.319 1。故最大干物质积累速率为主要决策变量(直接决定作用排第二),其原因是相比快增期结束时间(直接决定作用排第一),它受到其他因素的制约较少。因此,要从水氮调控角度提高向日葵产量,首要考虑通过更好的水氮调控措施来提高最大干物质积累速率,然后再考虑协调最大干物质积累速率出现时间与快增期结束时间的矛盾,以使更早达到最大干物质积累速率,更晚结束快增期。
通过多元线性回归分析得到的结果与赵姣等[33]在冬小麦上的研究结果一致:地上部干物质积累最大速率越高,产量越高;快增期结束时间离收获期越近,越有益于产量的提升。
挖掘干物质积累和产量的关系一方面可以指导灌水施氮方案的设计和农艺措施的设定,另一方面可以在具体栽培过程中根据田间实时采集到的数据进行灌水追氮的指导。得益于作物的地上部干物质积累量与作物的表观数据关联大,且表观数据不用破坏性取样且易于收集,比如无人机和卫星遥感技术[35-36]在这方面的应用。因此,从干物质积累角度出发研究增产决策是很好的切入点。
4 结 论
1)Richards 模型可以较为准确的模拟向日葵地上部干物质积累的动态过程。建立产量与干物质积累特征参数的多元回归关系y=272.209-5.450X1+49.370X2+7.376X7。
2)水氮调控地上部干物质积累进而提高产量的决策:首要考虑通过更好的水氮调控措施来提高最大干物质积累速率,然后再考虑协调最大干物质积累速率达到峰值的时间与快增期结束时间的矛盾,以使更早达到最大干物质积累速率,更晚结束快增期。
3)施氮使向日葵提前进入干物质积累快增期,但是过量施氮相较于优化施氮(养分专家推荐施氮量)会延后迟进入快增期并提前结束快增期,从而使快增期持续时间缩短。
4)较不灌水的处理,苗期和现蕾期的灌水使进入快增期的时间延后但积累速率更高,花期和灌浆期的灌水使快增期结束时间延后。苗期和现蕾期适当的补水,花期和灌浆期始终保持亏缺会使快增期的持续时间缩短。
(作者声明本文无实际或潜在的利益冲突)
