基于LESO的新型自适应鲁棒滚转通道控制算法

2023-08-08王治霖王江祁琪范世鹏

兵工学报 2023年7期

王治霖, 王江, 祁琪, 范世鹏

(1.北京理工大学宇航学院, 北京 100081; 2.无人机自主控制北京市重点实验室, 北京 100081;3.北京航天自动控制研究所, 北京 100854)

0 引言

相对于一般飞行器,导弹由于不具备强滚转稳定的姿态,当存在安装误差或受到外界扰动时,导弹滚转角速率极易发生变化。对于绝大部分导弹而言,导弹的滚转状态需保持稳定,滚转运动存在下导弹产生的马格努斯效应会加大俯仰和偏航通道间的耦合效应,增加导弹控制系统的难度。导弹的平动和角动力学方程也表明,只有当滚转角速率足够低时,俯仰和偏航通道的相互作用才能被忽略[1]。此外,导弹的滚转也会对导引头目标跟踪的准确性以及非对称导弹的稳定性等因素造成严重的影响[2]。因此,保持导弹的滚转姿态稳定是导弹控制系统中的关键一环。

导弹飞行过程中,存在气动参数不确定性、非线性动力学、外部干扰、未建模动力学以及量测误差等问题。对于导弹拦截/突防能力需求逐步增强的现代战场而言,导弹需要在多空域下进行大攻角高速机动,滚转通道动力学模型的强非线性和气动参数的不确定性表现更为明显[3],这无疑大大增加了滚转通道的控制难度。在这样的条件下设计能够保证整个飞行包络线滚转姿态稳定的滚转自动驾驶仪,是一个极具挑战性的问题。

针对导弹滚转驾驶仪的设计,传统方法基于根轨迹或频域分析方法,选取特征点进行自动驾驶仪设计,在此基础上进行增益调度以适应全弹道。其中特征点的选取以及自动驾驶仪参数调节需要丰富的工程经验作为支撑,同时在弹道末端存在增益变化较快、舵输入大幅度振荡的问题,准确性和稳定性较差。对于大攻角高速机动导弹的强非线性滚转通道动力学模型,采用传统方法已无法满足鲁棒性和适应性的要求。

随着现代控制理论引入导弹自动驾驶仪设计,H无穷方法[4]、μ综合方法[5-6]以及最优控制方法[7]都为滚转通道驾驶仪设计带来了一定改进。为进一步解决非线性模型的控制问题,Tipàn等将动态逆方法引入模型具有强非线性的双自旋导弹驾驶仪设计中[8],但未能有效消除通过动态逆对系统进行伪线性化过程中产生的误差。Jiang等通过神经网络与动态逆相结合的方法对飞行器姿态控制系统进行设计,解决了动态逆方法中存在的逆系统建模误差问题,但由于神经网络方法设计过程中对样本量的高度依赖,使用条件较为苛刻[9]。

随着滑模变结构方法的快速发展,该方法具有较快的响应速度,对外部干扰、未建模动态不确定性有很好的鲁棒性。因其显著的优点,滑模变结构控制被广泛地应用到飞行器姿态控制问题中[10-12]。但由于滑模控制方法缺乏对扰动的估计,单纯使用滑模方法的控制系统属于非连续控制,极易出现抖振现象,同时易对扰动产生过度补偿或高增益问题。Hua等针对参数不确定和执行器饱和条件下的滚转导弹控制问题,结合反步法设计了辅助系统,有效补偿了输入饱和引起的非线性项,但该方法是在小扰动假设下进行的低速滚转弹控制系统设计,亦未在不同飞行条件下对控制系统进行验证[13]。Han等设计了一种STT导弹的2阶滑模控制方法,有效抑制了外界干扰和系统的不确定性,并通过Twisting方法抑制了抖振[14],但上述方法需在假设攻角和侧滑角都很小的条件下才能实现滚转通道稳定控制,无法用于大攻角机动导弹。因此设计一种能对扰动进行准确估计,并在大攻角条件下能够实现自适应鲁棒控制的滑模控制方法,极具研究价值。

为解决上述问题,许多干扰估计方法如时滞估计(TDE)[15]、未知输入观测器(UIO)[16]、干扰观测器(DOB)[17-18]、扩张状态观测器(ESO)[19]、神经网络[20]和模糊逼近[21],被提出用于干扰的估计和补偿。在这些方法中,DOB是一种基于模型的方法,其增益难以调整;TDE需要以精确的加速度信号为基础,并且忽略了一个采样周期内的内部动力学;神经网络和模糊逼近方法比较复杂,收敛速度相对较低;UIO需满足观测器匹配条件或借助构造辅助输出等方法才能用于观测,设计繁琐复杂,实际应用难度较高。与其他技术不同,ESO可以同时估计系统的状态和不确定性,且不需要过多关于系统的信息[19]。

鉴于这一特性,综合精度和工程可实现性,本文采用线性扩张状态观测器(LESO)对系统扰动进行准确估计,通过新型滑模控制律中自适应项的快速调节实现干扰的动态补偿,降低观测器估计误差对系统的影响,削弱抖振的同时保证系统的鲁棒性。进一步地,考虑执行机构失效故障情况下的滚转通道控制,在不同失效程度下验证控制算法的有效性。仿真结果表明,本文方法能够满足复杂飞行条件下导弹控制系统的鲁棒性和自适应性需求,并具备一定的容错控制能力。

1 滚转通道数学模型

滚转通道动力学模型采用微分方程的形式可以表示为

(1)

表1 动力学模型参数

当滚转角等于0°时,该动力学模型为线性模型,很容易设计线性控制器使系统实现期望的控制性能。但当进行大攻角高速机动时,非线性项Clr(Ma,α)sin(4φ)的存在使得传统线性控制方法很难满足精度要求。因此,本文设计一种线性扩张状态观测器,将气动扰动等因素视为干扰,对其进行估计和补偿。同时提出一种自适应滑模控制律,通过自适应项的快速调节实现不同飞行条件下滚转角和滚转角速率的快速收敛。进一步考虑执行机构故障,满足了大攻角机动飞行条件下,气动扰动参数剧烈变化时滚转通道的自适应性需求,得到新型自适应鲁棒滚转通道控制方法。

针对传感器动力学滞后问题,传感器的动力学及考虑传感器动力学的滚转通道动力学模型如下:

(2)

(3)

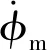
(4)

考虑到执行机构故障失效现象,可以将舵偏角表示为

δα=fu+Δδ

(5)

式中:0.3≤f≤1为执行机构的故障失效系数;u为待设计控制方法;Δδ为模型误差。当f=1、Δδ=0时,表示未发生执行机构故障失效。定义υ=δα,并引入执行机构失效模型式(5),得到

υ=fu+Δδ

(6)

(7)

式中:d2=Clr(Ma,α)sin (4x1)+Δδ+d1+ωRRf(ωg,ξg,φm)。

至此,考虑执行机构失效和传感器动力学的滚转通道控制模型建立完毕。

2 扩张状态观测器

2.1 扩张状态观测器的设计

Han[19]、韩京清[24]提出的扩张状态观测器设计方法对系统动力学信息需求较少,且具备较低的实施和设计难度,因此本文将设计线性扩张状态观测器用于估计系统中的未知动力学项d2。在设计该扩张状态观测器之前,对系统给出不失一般性的如下假设。

λ∈Ωλ{λ:λmin≤λ≤λmax}

(8)

式中:λmin和λmax均为已知常数;Ωλ为λ的取值集合。

为设计扩张状态观测器,定义一个新的变量x3=d2,并将式(7)转化为

(9)

式中:λ=Kδf。式(9)可以整理为矩阵形式

(10)

式中:

(11)

线性扩张观测器可以设计为

(12)

式中:e1为观测器误差;y为x1的实际值;z=[z1z2z3]T为扩张状态观测器的状态量;β1～β3为扩张状态观测器的增益,

(13)

ω0为扩张状态观测器增益的唯一相关参数,通过改变ω0取值可以对扩张状态观测器的效果进行调节。

2.2 扩张状态观测器的稳定性

在未知动力学项导数有界的假设成立条件下,Zheng等[25]对传统线性扩张状态观测器的稳定性和收敛性进行了证明,本文涉及的模型仅有已知动力学项Σ与之不同,根据文献[25]能够直接证明定理1,在此不再给出详细证明过程。

3 控制器设计

3.1 新型自适应鲁棒滑模控制器设计

滑模控制方法可以很好地处理系统参数不确定性和非结构不确定性。本文提出一种新型自适应鲁棒控制方法来处理导弹滚转通道控制中的不确定性问题,利用扩张状态观测器来估计并通过自适应滑模控制律补偿系统的未知动力学项等扰动带来的影响,从而保证导弹滚转通道控制的性能。控制器结构如图1所示。图1中,e为位置跟踪误差,=[123]T为矢量x=[x1x2x3]T的估计。

图1 控制器结构图

定义位置跟踪误差变量为

e=x1-x1d

(14)

式中:x1d为期望轨迹。

根据跟踪误差变量,定义滑模面为

(15)

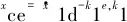
对变量s进行微分,可得

(16)

为处理系统中视为总干扰的强非线性项和参数不确定性项等未知动力学项,通过设计的扩张状态观测器得到扰动估计值,并将其用于补偿系统中的未知动力学项。基于扩张状态观测器,本文提出的新型自适应鲁棒控制器如下:

(17)

式中:uf包含了已知的动力学项F0和由扩张状态观测器估计得到的扰动项3;ur1用于对名义系统起到镇定作用;ur2是待设计的自适应控制项,用于消除状态扩张观测器误差产生的影响;kb为待设计参数。

将式(17)代入式(16),可得

(18)

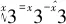
根据定理1,即使选择合适的观测器增益参数ω0,扩张状态观测器仍会存在一定的估计误差。为减小该部分估计误差对控制系统带来的影响,本文提出一种针对自适应控制项ur2的新型自适应控制律如下:

(19)

式中:η和μ为待设定参数;kr为自适应参数,当系统状态未处于滑模面时,增益将持续增大,加速趋近滑模面,在系统动态过程中,增益随|s|的减小而降低。

同时,为了降低抖振现象,在实际实施过程中可以使用边界层饱和函数sat(s,Φ)来替换符号函数sgn(s)。

(20)

式中:Φ为调节参数。

3.2 控制器稳定性证明

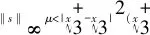
证明首先,选择正定的Lyapunov函数V为

(21)

根据式(18),可得Lyapunov函数V的1阶导数为

(22)

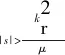
(23)

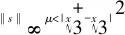
(24)

将式(23)代入式(22),可得

(25)

综上,可以证明本文所设计的控制器是最终一致有界的。

4 仿真与验证

本节通过MATLAB软件进行数值仿真,设计多飞行条件下,执行器正常工作与执行器存在故障时的系统仿真实验,验证所设计的新型自适应鲁棒滑模控制方法的有效性。综合考虑观测器的快速性和抗干扰能力,以及控制器的快速性和稳定性,选取如表2所示的相关控制参数。

表2 控制参数设置

不同飞行条件下滚转通道扰动参数的变化情况如图2所示。由于扰动系数受高度的轻微影响,导弹在发动机关火前后即速度峰值附近,存在一个速度大小相同但导弹所处高度不同的阶段,因此图2(a)末端同一速度对应了两个扰动系数值,即折线部分。

图2 滚转通道参数变化情况

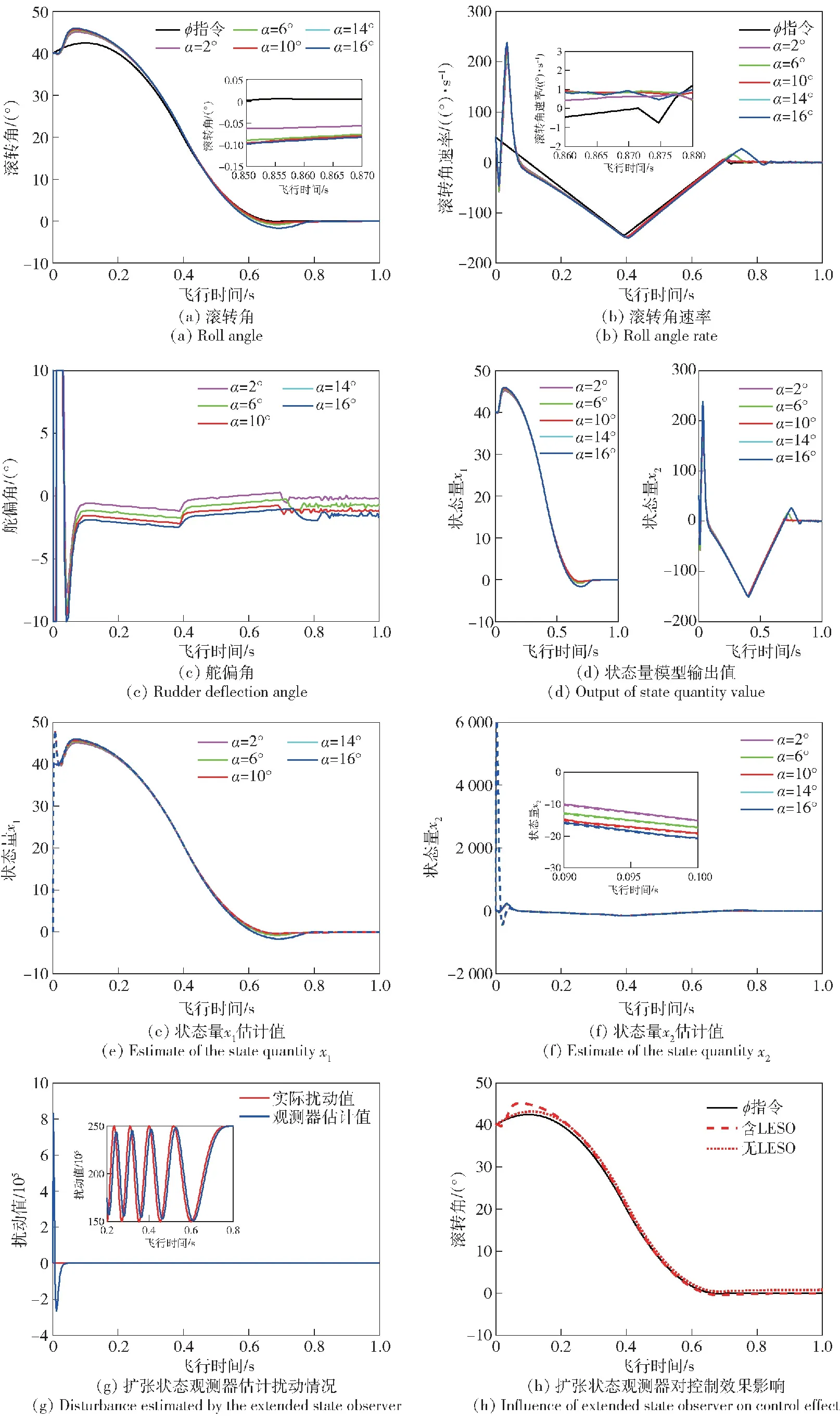
图3 不同飞行条件下滚转通道控制系统仿真

结合图3(a)和图3(b),在5种不同飞行条件下,本文设计的控制器均能使滚转角和滚转角速率分别在0.6 s和0.7 s前收敛至0°/s附近,验证了该算法的鲁棒性、快速性及较高的控制精度。

为验证线性扩张状态观测器的估计效果,分别对模型输出量、状态量以及扰动估计效果进行仿真,图3(d)、图3(e)、图3(f)和图3(g)为仿真结果。图3(e)和图3(f)中实线为模型输出值,对应颜色的虚线为观测器估计值,可以看出观测器能够精确地实现对扰动和状态量的估计。

在攻角为16°时,扰动幅值最大,变化程度最剧烈,故选取此飞行条件对观测器扰动估计效果进行仿真验证,根据图3(g)可以看出此时扩张状态观测器也能够对扰动进行有效估计。图3(h)为分别对该条件下有无观测器存在的滚转通道控制系统进行仿真的结果,通过滚转角控制结果分析,本文设计的自适应鲁棒控制器通过扩张状态观测器和自适应滑模算法的结合,有效提高了控制系统的精度。

在η、μ两参数单独变化条件下对自适应参数变化情况进行了仿真,结果如图4所示,可以看出本文所设计的控制方法中的自适应参数可在较大跨域内短时间实现收敛,通过动态调节控制参数,实现系统良好的姿态控制。

图4 自适应参数变化情况

结合图4(a)和图4(b)可以看出,自适应参数在滑模面趋近和到达过程中自动调节,在趋近过程中快速增大使趋近速度加快,到达滑模面后适度减小,达到缩短调节时间和减小抖振的效果,同时从0.2 s前的初始段可以看出,在初值选取较标准值相差较大情况下,该自适应参数具备快速调节能力。

为更好地验证本文设计控制器的控制效能,在0.7马赫时分别在2°和16°攻角下对本文算法和传统线性控制算法进行仿真对比,滚转通道控制效果见图5。由图5不难看出:当攻角较小时,传统线性控制方法收敛速度难以满足实际需求,抗干扰能力差,且控制效果较差;当攻角较大时传统线性控制器稳态误差较大,控制效果差。

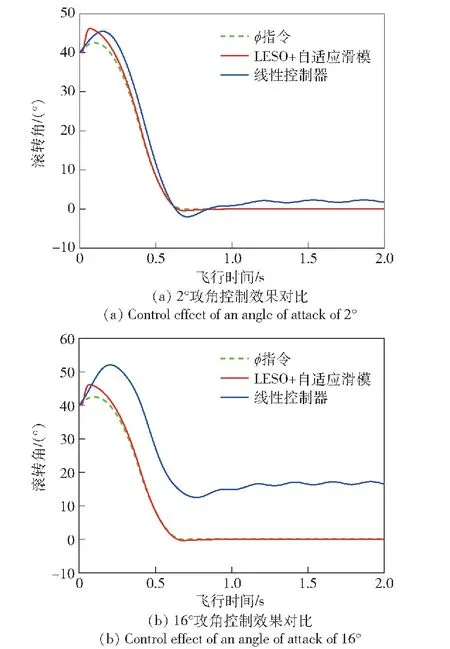
图5 控制效果对比

在此基础上,验证本文提出的控制方法可以自动判别当前故障受损情况,并自适应地通过调整控制量,最大限度地保证控制动态性能。在相同的初始滚转角和滚转角速率偏差条件下,考虑执行机构失效故障,分别对失效系数为f=0.3、f=0.5和f=0.9的滚转通道控制系统进行仿真,3个数值分别代表执行机构发生严重失效、中等故障和轻微故障的工况。各故障失效系数情况下的仿真结果如图6、图7和图8所示。

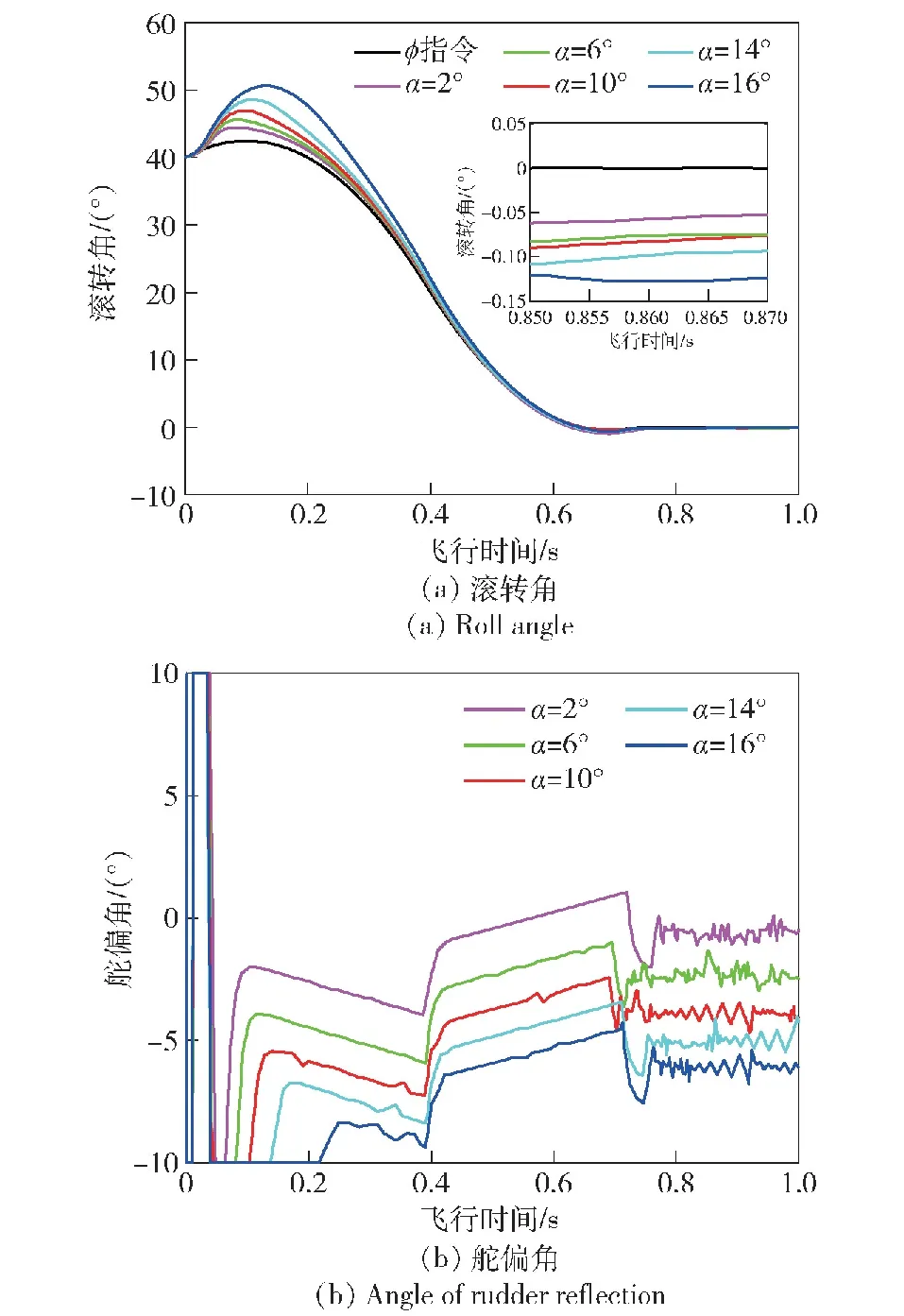
图6 f=0.3仿真结果

图7 f=0.5仿真结果

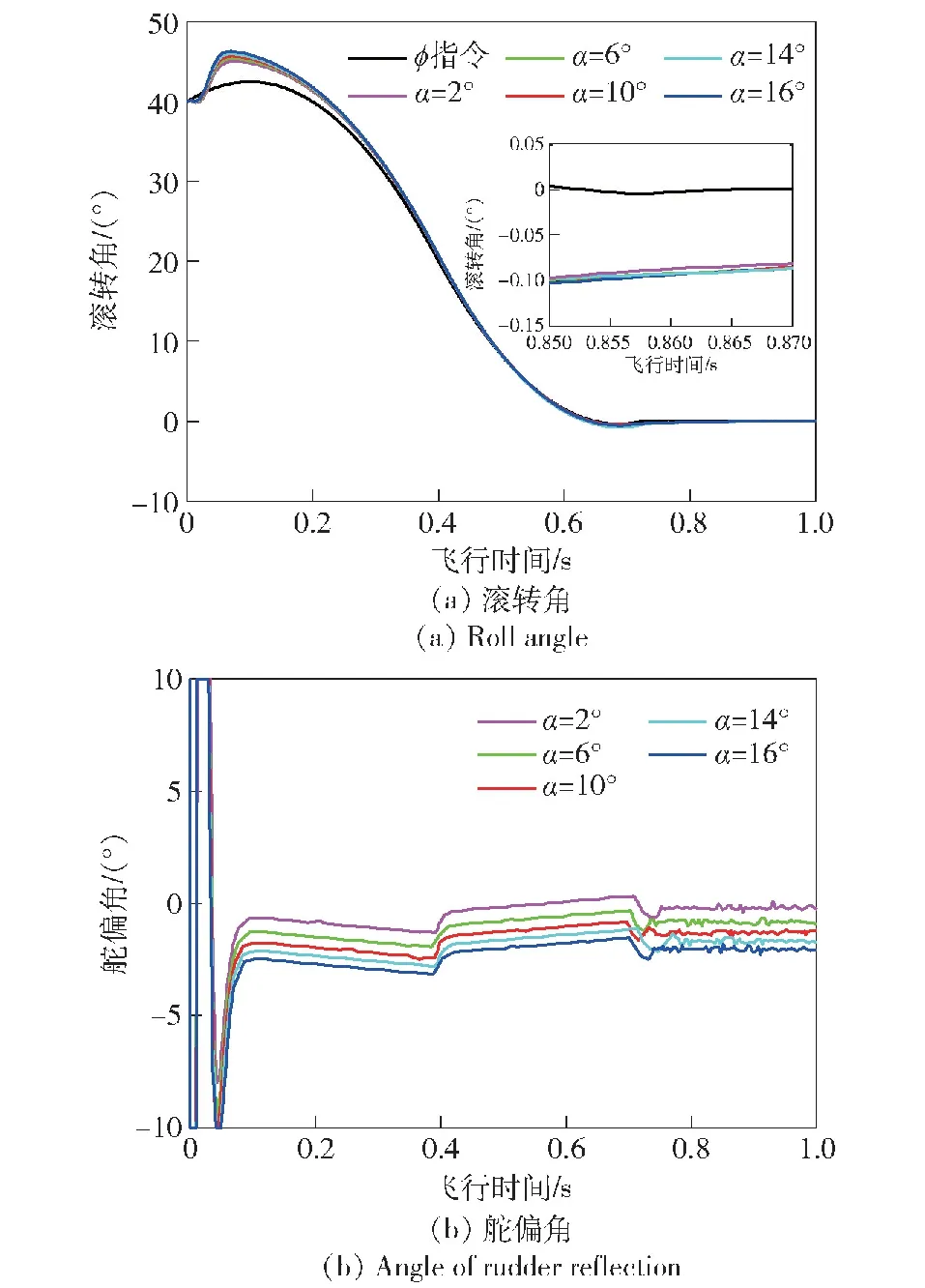
图8 f=0.9仿真结果

由图3(a)、图3(b)、图6、图7、图8可以看出,在失效系数为0.3的情况下,考虑不同攻角的飞行情况,滚转角分别约在0.85 s内收敛至0°附近,在失效系数为0.5的情况下,滚转角约在0.75 s内收敛至0°附近,在失效系数为0.9的情况下,滚转角约在0.8 s内收敛至0°附近。由于初始扰动估计值较大,导致初始调节阶段要求较大的输入值,但经验证可在执行机构偏转角度满足输入饱和限制条件下完成滚转通道稳定控制,如图6(b)、图7(b)和图8(b)所示。对比不同失效系数下的执行机构偏转角度可知,当失效严重时,执行机构增大偏转角度及较大舵输入下的控制时间,来弥补执行机构控制效率降低的影响,对于最终控制精度有较小影响,但对最终收敛时间无较大影响。针对不同失效系数下的滚转通道故障仿真说明,本文所设计的基于ESO的新型自适应滑模控制方法能够实现在执行机构失效情况下滚转角的快速收敛。