某飞机系统故障率敏感性分析研究

何勃，张文瀚，林健

（成都飞机设计研究所，成都 610091）

飞机在不同的服役阶段和使用环境下具有不同的故障率特征[1-2]，根据标准化后的历史外场使用数据，准确预测不同服役阶段和使用环境下的系统故障率，识别出影响故障率大小的敏感因素，可为系统故障预防、故障诊断和故障维修提供依据，对飞机完好率和出勤率的提升具有重要意义。传统的以使用时间为自变量的故障率分析模型只能给出装备的理论故障率变化趋势，而综合考虑已使用年限和使用环境信息的故障率分析模型能为飞机的故障率预测提供更加可信的依据。

对于我国大部分内陆地区，使用环境对飞机系统故障率的影响主要体现在温度、湿度和气压因素上。温度因素对飞机系统的故障率影响体现在多个方面，如对于电子产品，高温环境下元器件损坏、参数漂移的概率增加；对于机械产品，高温环境下运动机构卡滞、摩擦副过热的概率增加，低温环境下系统密封性能下降，温度剧烈变化带来的配合关系变化，均会导致系统故障率上升。湿度对飞机系统故障率的影响主要体现在高湿环境下机载产品和机体结构更易发生锈蚀故障，线路及电子元器件凝结冷凝水，造成短路故障率上升。气压对飞机的故障率同样存在影响，低气压环境下，发动机起动所需功率增大，刹车系统负荷增加。另外，对于机载制氧制氮系统，气压对其故障率也有着重要影响。

飞机系统故障率的影响因素较多，影响关系复杂，且不确定，对飞机系统故障率进行敏感性分析，识别故障率各影响因素的重要度，对飞机的外场使用具有重要指导意义。敏感性分析可分为两大类：局部敏感性分析和全局敏感性分析[3-4]。局部敏感性可定义为输出变量对输入变量在固定位置的偏导，该方法简单直观，但当模型非线性较强，且输入变量维度较高时，可能会得到错误的分析结果。全局敏感性分析方法通过探索输入变量的全部分布区域来分析模型的输出变化，不依赖于输入的位置信息，其中Sobol法是一种较为常用的全局敏感性分析方法[5-6]。在利用Sobol 方法解决敏感性分析问题时，根据各影响变量确定样本的故障率大小则是分析的前提。近年来，代理模型的应用可有效解决该问题。常用的代理模型有响应面、支持向量机、神经网络和Kriging，其中Kriging 是一种较为精确的插值统计模型，在系统的响应预测中已被广泛应用[7-9]。

本文对飞机系统的故障率敏感性分析问题进行了研究，综合考虑飞机服役阶段和使用环境，以飞机已使用年限和任务地点的自然环境数据为输入变量，故障率为输出变量训练Kriging，可以根据标准化后的历史外场数据来预测不同使用年限及使用环境条件下的飞机系统故障率。在进行飞机系统故障率敏感性分析时，通过利用Kriging 对随机矩阵中各样本点的故障率进行预测，可以更加高效地计算各输入变量的敏感性指标，为飞机系统故障预防、故障诊断和故障维修提供依据。

1 方差分解

假设模型输出响应为Y=y(X)，其中X={X1,X2, …,Xn}，为服从概率密度函数f(X)的n维变量。根据高维模型描述，y(X)可分解为[6,10-11]：

其中：

其中：X～i为除Xi外的其余变量。当X1,X2,…,Xn之间相互独立时，式（1）等号右边各项正交。因此，对式（1）等号两边取方差可得：

其中：

式（3）等号两边同除以V(Y)，可得：

其中：

Si定义为主指标，也称一阶效应指标；Sij=Vij/V(Y)，为二阶指标，表征变量Xi和Xj间的二阶交叉效应。类似地，s阶指标可解释为s个变量对输出方差的s阶交叉效应。文献[6]中又提出了全效应指标：

根据全方差公式[12]：

则全效应指标为：

2 Kriging 代理模型

2.1 Kriging 模型的基本思想

Kriging 模型可以作为黑箱函数来预测n维输入变量X的输出g(X)[13]，其在敏感性分析中的效率已经被证明[14-15]。Kriging 模型可分解为线性回归部分和随机过程[16]：

式中：f(X)=[f1(X),f2(X),….,fm(X)]T称为基函数；β=[β1,β2,…,βm]T为回归向量矩阵；fT(X)β表示输出的平均近似；Z(X)表示回归模型的偏差模拟。假设为静态高斯随机过程，样本Xk和Xj的协方差为：

其中，k,j=1,2, … ,N，σ2为方差，R(·,·)为高斯相关函数：

式中：θl是相关参数；Xkl和Xjl为向量Xk和Xj的第l个分量。

参数β和σ2可通过式（13）、（14）估计：

式中：F是由f(X)在训练样本点的评估值组成的向量；g为对应输出；R为相关矩阵；Rk,j=R(Xk,Xj)。Rk,j中的未知参数θl可以利用最大似然估计法计算：

Kriging 预测的期望值(X) 为g(X)的最优线性无偏估计：

其中，r(X)是相关向量，r(X)=[R(X,X1), …,R(X,XN)]。

2.2 基于训练样本点的Kriging 交叉验证

当利用Kriging 模型来预测样本输出时，模型的构造质量对预测精度起着决定性作用。为了得到更加精确的预测结果，在预测前需对Kriging 模型进行精度验证，最直接的验证方法就是随机抽取若干样本点作为测试点，通过比较测试点的预测值和真实值之间的误差来检验模型精度，但当测试点的真实输出值无法直接获取时，该验证方法则无法实施。因此，本文引入交叉验证法充分利用已有信息来验证Kriging 模型的精度。

交叉验证的主要思想：对于N个已知真实输出值gT={g(X1),g(X2), …,g(XN)}的训练样本XT={X1,X2, …,XN}，记除去第j个样本Xj外的其他N-1 个样本组成的集合为XT/Xj={X1,X2, …,Xj-1,Xj+1, …,XN}。基于N-1 个样本，XT/Xj与对应真实输出值gT/g(Xj)训练的Kriging 模型记为（X），模型（X）在第j个训练样本点预测的相对误差rj为：

依次计算所有训练样本的预测误差，则可以得到当前Kriging 模型的预测误差：

当利用交叉验证法验证Kriging 模型满足精度要求时，即rRPRESS＜Rs，则认为当前的Kriging 模型可用于预测样本输出，否则需再次增加训练样本数量来进一步提高Kriging 模型的预测精度。

3 敏感性指标的计算

3.1 直接法

敏感性指标最简单直观的计算方法为直接法，首先应用蒙特卡洛法根据输入变量的概率密度函数f(X)生成Nin组样本，将每个样本Xi分别固定在Nin个不同点上。再根据蒙特卡洛法对X～i抽取Nout组样本，并计算，然后根据Xi的Nin个样本对应的计算，最终可利用式（6）得到输入变量Xi的主效应指数。

根据上述分析，当采用直接法来计算时，对于n维输入变量X1,X2, …,Xn,共需n×Nin×Nout次样本输出值计算。假设得到总方差还需2k次样本输出计算，则直接法计算主效应指标总共需2k+n×Nin×Nout次样本输出值计算。采用直接法计算全效应指标与上述过程相同。

3.2 Sobol 法

当n维输入变量X1,X2,…,Xn相互独立时，可以利用Sobol 法来计算各敏感性指标。记A和B为2 个相互独立的随机抽样矩阵：

其中k为抽样次数，根据文献[17]和[18]，有：

对于总方差，有：

将式（22）和（23）分别代入式（6）和（9）则可得到输入变量Xi的主效应指标和全效应指标。

4 故障率敏感性分析方法

装备故障率主要受服役阶段及使用环境因素的影响[19]，在飞机外场保障中，系统的故障率预测对飞机的使用维护具有至关重要的意义。飞机系统的故障率P可根据单位日历时间内系统发生的故障次数及工作时间计算：

式中：n为单位日历时间内的系统故障数量；h为单位日历时间内的系统工作时间。

根据装备或产品使用规律，其故障率会随服役阶段发生变化。例如，对于大部分机械产品，其故障率趋势一般呈现浴盆曲线特征，主要分为早期失效期、偶然失效期和耗损失效期3 个阶段，所以服役阶段为影响装备故障率特征的一个重要因素。对于我国绝大多数内陆地区，环境因素对故障率的影响主要体现在温度、湿度和气压3 个因素上。原始的使用环境数据为按固定时间间隔采集的一系列数据序列，数据规模庞大，无法直接用于系统故障率敏感性分析。为了提高环境数据处理效率，有必要从环境数据序列中抽取统计特征，首先选取平均温度、平均湿度和平均气压作为故障率敏感性分析的变量，同时根据装备的外场使用经验，温差也会引起系统的故障率变化，平均温差也应作为故障率敏感性分析的变量。因此，飞机系统的故障率P可表示为：

式中：X1为使用年限；X2为平均温度；X3为平均温差；X4为平均湿度；X5为平均气压。

由于真实的故障率函数g(X)无法获得，文中采用Kriging 模型来预测故障率g(X)的数值，使用年限、平均温度、平均温差、平均湿度和平均气压则作为Kriging 模型的输入。将Kriging 模型引入Sobol 方法，用Kriging 预测Sobol 法中随机矩阵各样本点对应的故障率，并以此来计算各输入变量的敏感性指标。该方法首先建立初始Kriging 模型，并通过交叉验证来保证初始Kriging 模型具有一定置信度来预测样本矩阵A、B、和中各样本的故障率，进而得到各输入变量的敏感性指标。综上，为以更高的计算效率得到满足要求的故障率敏感性指标，发展了以下的计算程序：

1）分别按时间周期T采集飞机系统在不同使用环境下的环境数据，包括环境温度、湿度和气压数据序列，并统计飞机系统的已使用年限及每个周期T内对应的工作时间和故障数量。

2）计算每个周期T内采集的温度、湿度和气压数据序列的统计特征，即平均温度、平均温差、平均湿度和平均气压，以及对应的故障率。

3）根据第2 节中Kriging 模型参数建立Kriging模型。相关模型选择为高斯模型，回归模型选为常数。文中Kriging 模型借助于DACE 工具箱[20]建立。

4）将不同周期T对应的系统已使用年限、平均温度、平均温差、平均湿度和平均气压及故障率作为训练样本，对Kriging 模型进行训练。

5）根据式（19）计算当前Kriging 模型的预测误差rRPRESS。判断rRPRESS＜Rs是否满足。若不满足，则前往步骤1）继续收集训练样本；若满足，则前往步骤6）。

6）利用蒙特卡洛方法根据使用环境及使用年限的统计分布生成k组样本点，组成随机矩阵A。再次利用蒙特卡洛方法根据使用环境及使用年限的统计分布生成k组样本点，组成随机矩阵B。

7）将随机矩阵A和B的所有样本点（矩阵中的每一行）组成的集合记为St，利用Kriging 模型预测St中每个样本点对应的故障率。

8）根据Kriging 模型预测的St中各样本点的故障率计算V(Y)。

9）令i=1，将矩阵和中所有样本组成的集合记为S(i)，利用Kriging 预测S(i)中每个样本的故障率。

10）根据Kriging 对S(i)中各样本的故障率预测结果，利用式（6）和（9）计算变量Xi的主效应指标Si及全效应指标。判断i=n（n为输入变量个数）是否满足，若满足，则结束算法；否则令i=i+1，回到步骤9）。

飞机故障率敏感性分析方法的流程如图1 所示。虽然Sobol 方法较直接法在计算效率上已有极大提高，但由于目前积累的外场故障率样本数量较少，无法满足直接应用Sobol 方法进行敏感性分析的要求，所以本文选取了训练代理模型作为黑箱函数预测的方法来对Sobol 方法抽取的已知使用年限和环境变量的样本进行故障率预测。在代理模型中，Kriging 模型因为计算量相对较小，且在大量文献[7,9]中被证明对非线性复杂问题等具有较好的近似效果，所以本文选取了Kriging 模型来预测Sobol 方法中所需样本的故障率。

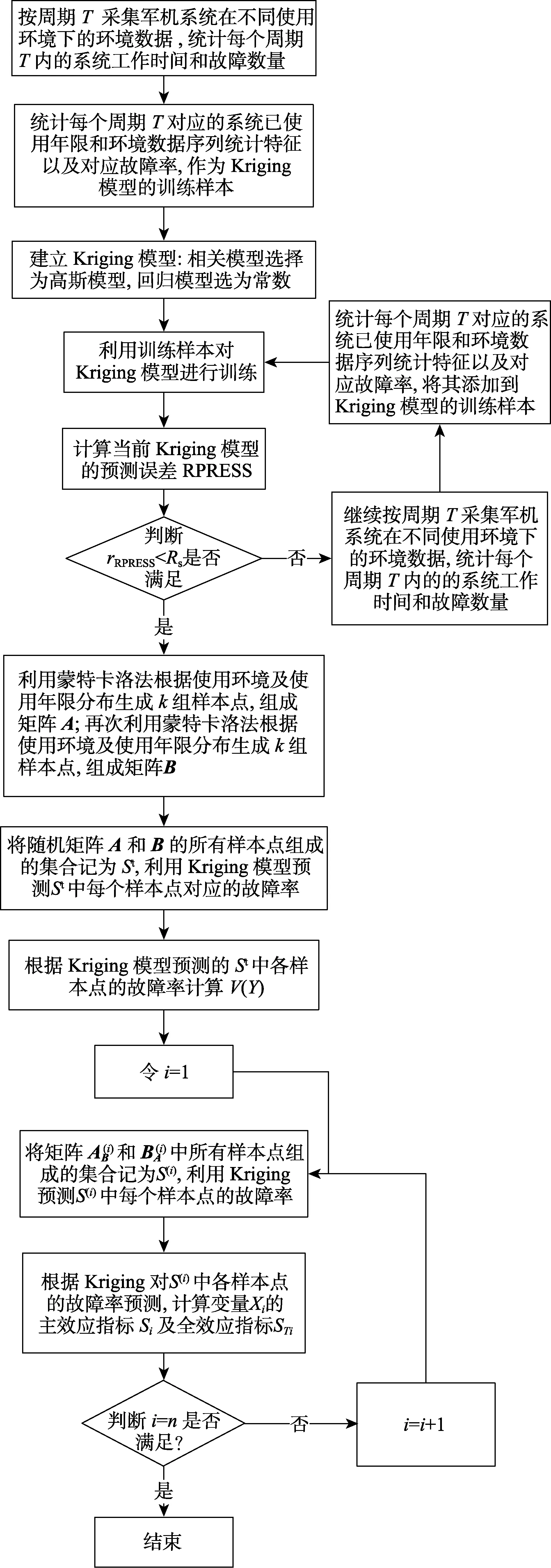
图1 飞机系统故障率敏感性分析程序Fig.1 Flow chart of sensitivity analysis for aircraft system failure rate

5 应用研究

本节统计了2016—2018 年某飞机子系统外场不同服役阶段和使用环境下对应的系统故障率数据。时间周期T取为日历月，每个时间周期内按6 h 时间间隔采集温度、湿度和气压数据，根据采集的环境数据序列计算每个周期对应的使用环境统计特征，即平均温度、平均温差、平均湿度和平均气压。同时统计每个时间周期T内系统故障数量及系统工作时间，进而得到每个时间周期T对应的系统故障率P。以每个时间周期T对应的已使用寿命和使用环境统计特征及其故障率作为训练样本，本算例中共计收集了144 组样本，样本的故障率数据如图2 所示。

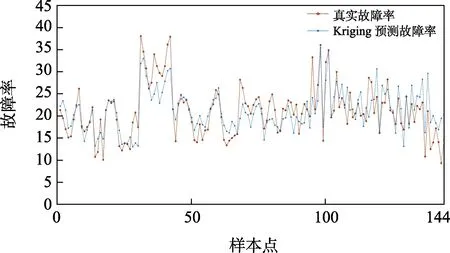
图2 交叉验证过程中样本点的Kriging故障率预测值与真实值比较Fig.2 Comparison between the value predicted by Kriging and the actual value of sample in the cross-validation process

5.1 故障率预测模型建立

根据144 组训练样本及对应故障率建立并训练Kriging：相关模型选择为高斯模型，回归模型选为常数。采用交叉验证策略（143 组建模，1 组验证）对初始 Kriging 模型进行精度验证：计算rRPRESS为0.036，可满足故障率预测要求。图2 中对交叉验证过程中各样本点的Kriging 故障率预测值与真实值进行了比较。

5.2 故障率影响因素敏感性分析

5.2.1 故障率影响参量的分布

影响飞机系统故障率的变量包括使用年限、平均温度、平均温差、平均湿度和平均气压，各变量的分布范围参考系统的实际使用工况给出，分布形式选取为均匀分布，分布参数见表1。

表1 故障率影响因素的分布参数Tab.1 Distribution parameters of the factors affecting failure rate

5.2.2 Kriging 模型对随机抽样矩阵的预测

利用蒙特卡洛方法，根据表1 中系统故障率影响变量的分布抽取样本点，组成随机矩阵A和B（样本数选为106），基于5.1 节训练完成的Kriging 模型预测矩阵A和B组成的样本集St中每个样本点的故障率，根据Kriging 对样本集St的每个样本的故障率预测值计算总方差V(Y)。完成总方差V(Y)的计算后，继续利用当前 Kriging 模型预测和(i=1,2,…,5)组成的样本集S(i)中每个样本的故障率，然后根据样本群S(i)中每个样本的故障率预测值计算及，进而得到该系统故障率5 个影响变量的主效应指标和全效应指标，见表2。

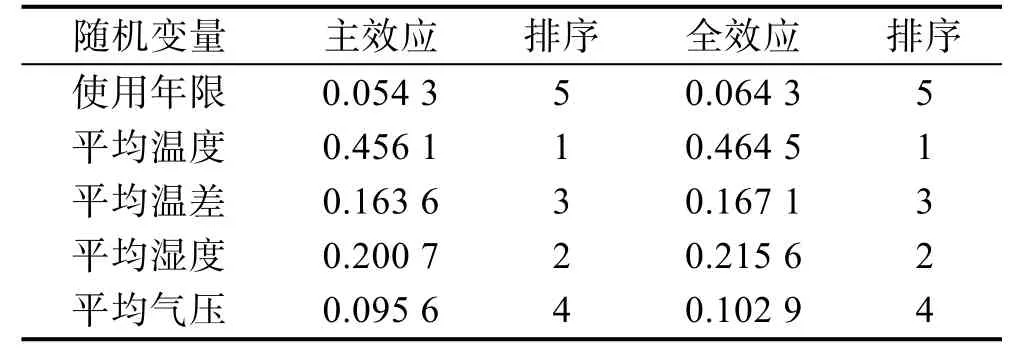
表2 故障率影响变量的主效应指标及全效应指标Tab.2 Main effect and total effect indexes of the failure rate variables

5.2.3 分析结果讨论

从表2 中该系统故障率的敏感性分析结果来看，各影响变量的主效应指标与全效应指标的排序较为一致，根据各输入变量的重要度排序可以定性地比较各输入变量对系统故障率的影响大小。从主效应指标及全效应指标的排序结果来看，平均温度和平均湿度为对该系统故障率影响较大的变量。从设计角度来讲，要控制系统的故障率，这些变量应当是需要重点关注的。其他的一些变量，如平均温差和平均气压对故障率的影响较小，所以当需要降低故障率计算模型的输入变量维度或简化分析模型时，这些变量应是首先可以忽略的。

由于该算例中Kriging 训练样本的使用年限分布较多集中于系统的稳定运行期内，系统使用初期及接近寿命极限阶段内的样本量较少，导致Kriging 模型对这2 个阶段的信息学习不够。因此，从本文的敏感性分析结果来看，故障率对使用年限因素不够敏感，而这可能与实际使用经验不符。为解决该问题，后续需进一步收集系统使用初期和接近寿命极限这2 个时间阶段的故障率数据。

随着训练样本数量的增加，Kriging 模型的预测精度会逐渐提升，从已有的144 个样本中随机选取部分样本作为训练样本训练模型，并采用交叉验证策略验证模型预测精度。首先随机选取20 个样本作为训练样本训练模型，并计算rRPRESS，随后每次增加2 个训练样本数量训练模型并计算rRPRESS，直到最终采用144个训练样本训练模型，不同训练样本数量训练模型对应的rRPRESS值如图3 所示。从图3 中可以看出，随着训练样本数量增加，模型的rRPRESS值总体呈下降趋势，即模型的预测精度逐渐提升，可说明后续若能进一步增加训练样本数量则能得到更加精确的预测结果。

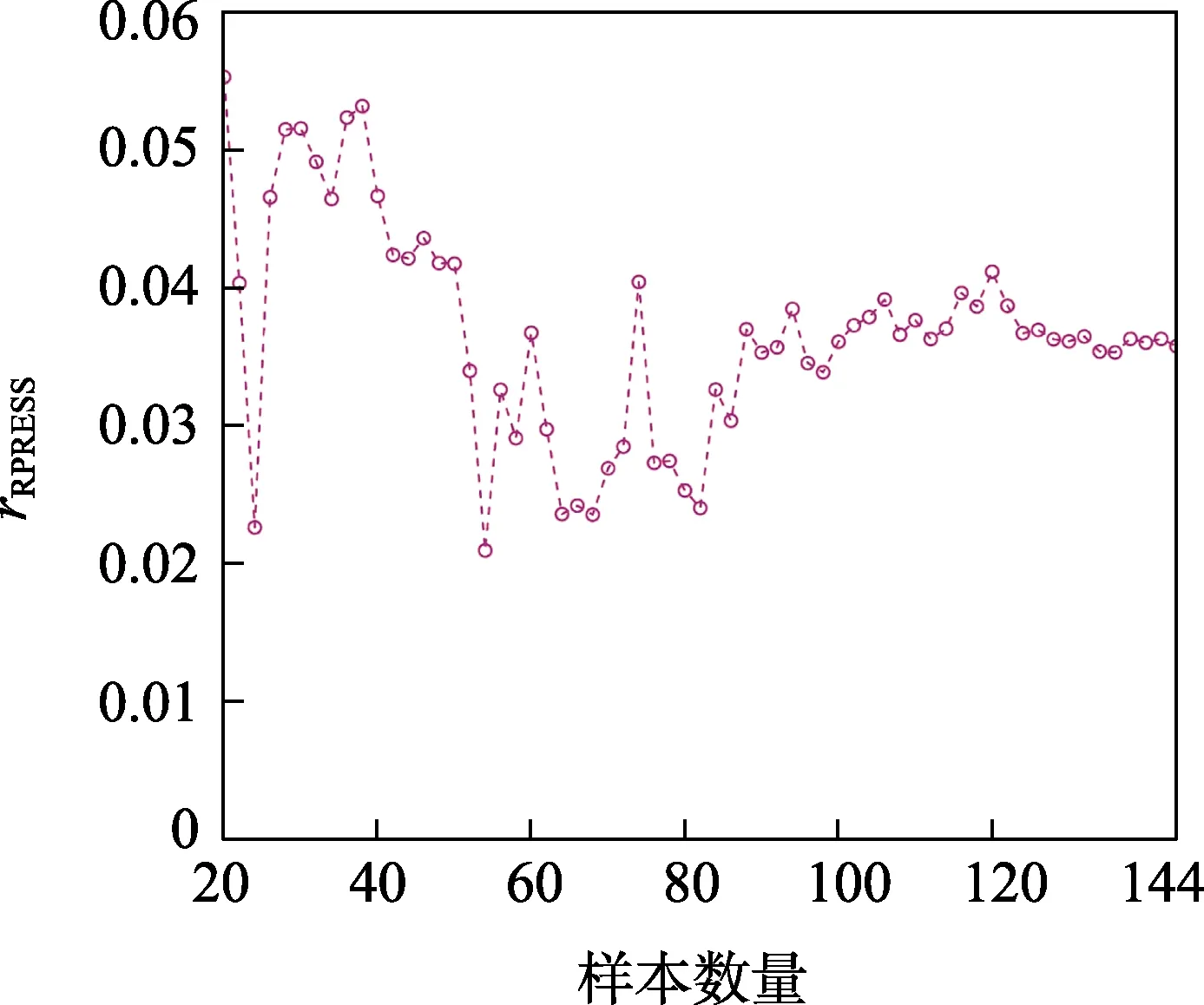
图3 训练样本数量对Kriging 故障率预测精度的影响Fig.3 Effect of training sample size on prediction accuracy of Kriging for failure rate

6 结语

本文对飞机系统的故障率敏感性分析问题进行了研究，结合Sobol 方法和Kriging 模型发展了一种适用于飞机系统故障率敏感性分析的方法。该方法通过收集不同使用年限和使用环境数据及对应的系统故障率，并将其作为训练样本训练Kriging 模型成为满足系统故障率预测要求的黑箱函数。然后通过利用训练完成的Kriging 模型预测敏感性分析所需的样本故障率，能有效避免真实故障率获取困难的问题，因而可以更加高效地计算输入变量的敏感性指标，并给出重要度排序，能很好地解决飞机系统故障率敏感性分析问题。最后，通过解决某飞机子系统的故障率敏感性分析问题，得到了影响系统故障率的各因素的主效应及全效应指标，证明了该方法在飞机系统故障率敏感性分析中的实际应用价值，可为飞机系统的外场维护使用及设计提升提供参考。