初中数学教学中学生逆向思维能力的培养路径

文/颜新凡

引 言

初中数学教学中，教师应充分认识到培养学生逆向思维能力的重要性。逆向思维在解题中有广泛应用，能帮助学生有效提高学习效率，提高学生思维灵活性[1]。为更好地培养学生的逆向思维能力，教师应引导学生做好逆向思维理论知识自主学习，理解逆向思维的外在表现，顺利实现培养目标。

一、借助理论灌输培养逆向思维能力

在培养学生的逆向思维能力时，教师首先应让学生了解逆向思维，认识到逆向思维的重要作用，以及在解题中的具体体现[2]。教学实践中，教师应注重将培养活动融入理论知识灌输中。一方面，在讲解相关运算法则时，教师不仅要要求学生理解运算法则，牢固记忆，还应给予学生有针对性的启发，使其能够逆向推导运算法则，对运算法则形成清晰认识，为逆向思维的应用奠定基础。另一方面，为使学生认识到逆向思维的重要性，教师应围绕教学重点，积极创设相关问题情境，与学生一起分析解决问题的思路与方法，使其体会逆向思维的应用过程，体会用逆向思维解题的便利性。

例如，“幂的运算”是初中数学极其重要的知识点，也是各类测试常考知识点。在讲解该部分知识时，为使学生牢固掌握运算法则，并能应用逆向思维解决相关问题，教师可创设以下问题情境，要求学生根据提示分析解答：将幂的运算运用逆向思维可得：am+n=am·an，am-n=am÷an，amn=(am)n，ambm=(ab)m。逆向运用幂的运算法则，有时可获得良好的解题效果。接着，教师让学生解答以下问题：

（1）若3×9m×27m=311，求m的值。

（2）已知a=255，b=344，c=533，d=622，则a、b、c、d的大小关系怎样？（已知当a＞b＞0，n为正整数，那么an＞bn）

该问题难度并不大，分析问题的关键在于能否根据提示逆向运用幂的运算法则。

问题（1）：根据幂的逆运算可知9m=32m，27m=33m，则3×9m×27m=3×32m×33m=35m+1=311，则5m+1=11，解得m=2。

问题（2）：由255=(25)11=3211，344=(34)11=8111，533=(53)11=12511，622=(62)11=3611，由125 ＞81 ＞36 ＞32，可得c ＞b ＞d ＞a。

二、借助例题讲解培养逆向思维能力

例题讲解是初中数学教学活动的重要构成部分[3]，既要巩固学生所学知识，又要有针对性地锻炼学生的逆向思维能力，给学生带来良好的解题启发，使学生积累逆向思维解答习题的经验[4]。逆向思维的表现形式较多，以初中数学几何知识为例，由几何图形推出几何图形的性质可看出正向思维，而从几何图形性质推出几何图形，则属于逆向思维。在此基础上，教师围绕教学内容做好课堂例题的筛选，通过例题展示由几何图形性质逆向构造几何图形的过程，能够使学生感受整个推理过程，把握逆向思维解题的关键。

例如，“圆”是初中数学中非常重要的几何图形，涉及的性质较多。在教学中，教师会要求学生整理相关性质并牢固记忆，同时运用多媒体技术为学生讲解如下经典例题：如图1，AB是圆O的直径，点C、D是圆O上不同于A、B两点的点，连接OC，OD，CD，过点C作CE⊥DB，交DB延长线于点E，连接AC、AD。（1）若∠ABD=2 ∠BDC，求证：CE是圆O的切线。（2）若圆O的半径是，，求AC的长。

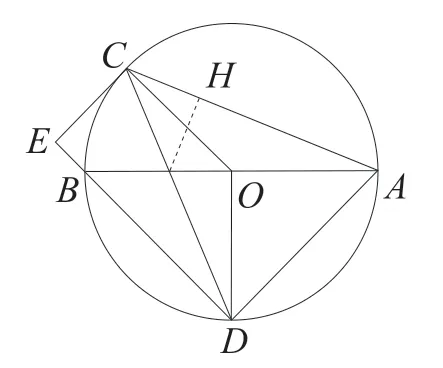
图1

（1）证明：根据同弧所对的圆心角是圆周角度数的2 倍，因为同BC弧，所以∠BOC=2 ∠BDC，因为∠ABD=2 ∠BDC，所以得出∠BOC=∠ABD，所以OC∥BD，所以∠DEC+ ∠ECO=180°，因为∠DEC=90°，所以∠ECO=90°，所以得出CE是圆O的切线。

（2）因为同BC弧，所以∠BDC=∠BAC，因为，所以，经 过 点O作OH⊥AC于H，因为tan，设OH=x，所以AH=2x，根据勾股定理可以得出，OH2+AH2=OA2，求解得出x=1，所以AC=4。

三、借助课堂训练培养逆向思维能力

为获得良好的逆向思维培养效果，在初中数学教学中，教师应注重将培养工作融入课堂训练活动中，给学生提供运用逆向思维分析问题的机会，使其通过逆向思维暴露出自身的不足[5]。一方面，教师要做好初中数学题型及学生解题方式的研究，做好课堂训练习题的针对性设计，引导学生突破思维定式，在逆向思维指引下解题。另一方面，在训练活动结束后，教师可要求学生做好训练总结及训练心得交流，分析逆向思维适用的问题情境、习题类型，以便以后遇到类似问题运用逆向思维迅速突破。

例如，在完成“数轴”知识讲解后，教师可设计以下课堂训练习题，要求学生作答：如图3 所示的数轴上，点A、B、C对应的数分别为a、b、c，若以下三个式子均成立：①|b|＜|c|；②a+c＜0；③a+b＜0，则原点的位置可能在（ ）。

图3

A.点A的左侧 B.点A和点B之间

C.点B和点C之间 D.点C的右侧

学生对数轴类的问题并不陌生。多数习题要求学生根据点在数轴上的位置进行相关计算。但是该习题另辟蹊径，给出相关参数的大小关系，要求推理原点位置。学生采用正向思维分析问题的难度较大，可以运用逆向思维从给出的选项入手，逐一验证其是否满足题干给出的三个式子，运用排除法顺利得出正确选项：

A 项，若原点在点A 的左侧，a、b、c均为正数，不满足②③，排除。B项，若原点在点A和点B之间，a＜0，c＞0，且|c|＞|a|，a+c＞0，不满足②，排除。C 项，若原点在点B和点C之间，可同时满足上述三个式子。D 项，若原点在点C的右侧，不满足①，排除。因此，选择C 项。

四、借助课堂小结培养逆向思维能力

课堂小结常用于总结课堂上讲解的知识点、相关的解题方法等，帮助学生系统认识所学知识[6]。在课堂小结环节，教师应注重对学生逆向思维能力的培养，一方面，引导学生对所学知识分门别类，尤其通过联系所学旧知识，构建新旧知识之间的内在关联，实现对学习内容的全面认识。同时，通过相关解题技巧的总结，学生在以后解题中能少走弯路，提高解题效率。另一方面，通过对课堂例题的改编，教师可引导学生采用逆向思维分析问题，锻炼运用逆向思维分析问题的能力。

例如，“解一元一次不等式组”是初中数学的重要知识点。通过课堂小结，学生认识到在确定不等式组的解集时，常按照“大大取较大，小小取较小，小大、大小取中间，大小、小大无处找”的法则。为培养学生的逆向思维能力，在课堂小结时，教师可对课堂例题做如下改编：若不等式组的解为-3＜x＜1，则(a+1)(b-1)的值为（ ）。

A.-6 B.7 C.-8 D.9

课堂例题讲解的是给出一元一次不等式组，求不等式组的解集。在课堂小结时，教师给出不等式组的解集，要求学生求对应参数的值，以锻炼学生的逆向思维能力。解题时，学生需先计算出a和b的值，而后将其代入要求解的式子。

五、借助日常作业培养逆向思维能力

在教学实践中，教师应借助作业培养学生的逆向思维能力。一方面，教师结合逆向思维能力培养目标做好作业习题设计，既要兼顾基础知识的考查，又要有针对性地锻炼学生的逆向思维能力。另一方面，为使学生尽快找到解题思路，提高做作业的信心，教师应注重给予学生有针对性的提示。

例如，在“一元二次方程”教学完成后，为加深学生对根与系数的理解，启发学生运用逆向思维解题，教师可为学生布置以下作业：已知实数s、t分别满足7s2+7s+1=0，t2+7t+7=0，且st≠1，则22的值为（ ）。

A.-1 B.0 C.1 D.2

该题难度较大，需逆向运用根与系数的关系构造出对应的二次方程，再运用根与系数的关系解答。教师可引导学生对给出的等式进行变形，构造对应的二次方程。最终学生根据提示运用逆向思维成功计算出结果。

由t2+7t+7=0，方程两边同除以“t2”得到：， 由7s2+7s+1=0， 可 知s和是方程7x2+7x+1=0 的两个根。由根与系数的关系可知。

六、借助数学测试培养逆向思维能力

在教学实践中，教师可通过测试习题的设计，培养学生的逆向思维能力。结合自身教学经验，教师可筛选或设计一些经典习题，在考查学生掌握所学知识牢固程度的同时，使学生运用逆向思维解答问题。不仅如此，在学生完成测试后，教师还应专门预留时间，让学生分析自身的解题思路，尝试运用逆向思维解题。

例如，化简求值是初中数学中的经典题型。在数学测试中，教师可适当提升习题难度，使学生从要求解的问题出发，采用逆向思维解题。如教师可设计如下习题：已知a、b、c均为实数，且，，求的值。

该题看似难度较大，很多学生无从下手。实际上，教师可采用逆向思维从要求解的问题入手，构建要求解问题与已知条件的联系。学生通过分析可知，需分别对式子进行取倒数处理。

结 语

综上所述，培养学生逆向思维能力的途径多种多样。为达到预期的培养效果，教师既要借鉴他人的经验，又要结合自身教学经验寻找适合自身的方法，不断总结经验教训，做好成功经验的推广及优化，将细节考虑到位，使学生的逆向思维能力得到有效提升。