城镇化地区公路改扩建交通安全状态评估研究

吴兴国

摘要 对城镇化地区公路进行改扩建，保障施工期间交通通行安全是关键。文章从人—机—环境系统工程理论角度出发，研究公路改扩建过程中人员、车辆、机械、环境等因素在不同安全状态下对交通安全的影响情况，将解模糊语言算法融入贝叶斯网安全评估体系，构建模糊贝叶斯网交通安全状态评估模型，量化公路改扩建施工期间交通安全状态，为相关部分采取安全防控措施提供决策依据。

关键词 改扩建；系统工程；模糊理论；贝叶斯网；安全评估

中图分类号 U418.8文献标识码 A文章编号 2096-8949（2023）14-0030-03

0 引言

城镇化地区公路一般为该区域对外联络的主要通道，改建必须以不中断交通的方式实施，其中所涉及人车环境等要素远比新建项目复杂得多[1-2]。显然，实时掌握施工过程中人员、车辆、机械环境等要素的安全状况，辨别可能存在的危险源，对于采取必要措施降低事故的发生的概率，充分保障施工期间通行安全显得尤为重要。

1 城镇化地区公路改扩建交通安全评估体系构建

1.1 交通安全影响评估节点

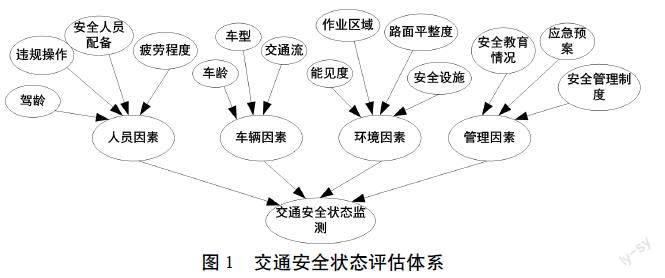
根据城镇化地区公路改扩建施工特点，对人机环境系统工程理论进行扩展，将人机环境系统中的“人”扩展为驾驶员和施工人员，“机”扩展为车辆，“环境”扩展为气候环境和施工作业环境，再将施工期间的管理因素加入系统，构建以交通安全状态评估为目标节点，人员、车辆、环境、管理为一级评估节点的评估体系，如图1所示。

1.2 节点安全状态级别划分

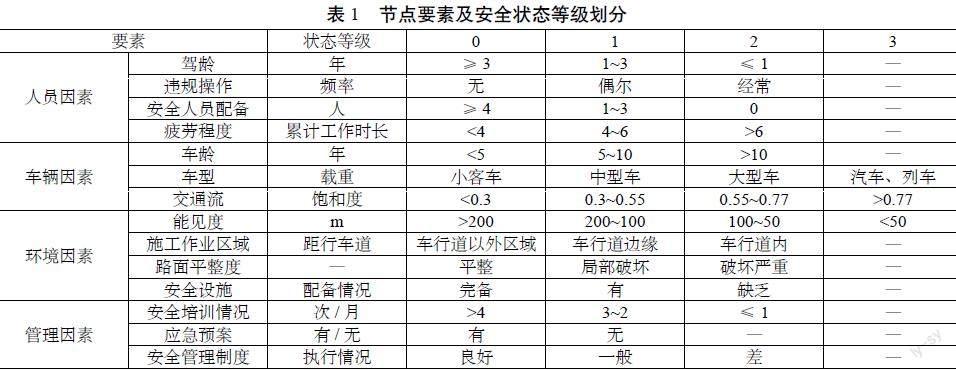
公路改扩建是一个涉及众多复杂要素的系统工程[3]。系统中各要素节点的安全状态决定了系统安全状态。该文采用数字0123…来区分要素节点的安全等级（如表1所示），数字越小，节点安全状态等级越高，发生事故的概率越小，说明对于改扩建期间交通安全运行是有利的；反之，节点安全状态越差，越不利于交通安全运行。

2 交通安全状态监测模型构建

2.1 多状态贝叶斯网络模型构建

贝叶斯网络又称贝叶斯信度网络[4-5]。网络节点表示一个随机变量，用条件概率表示兩个随机变量之间连接关系强弱。公路改建安全评估体系中节点有多个安全状态，属于多状态多节点的贝叶斯网结构。贝叶斯网的核心是贝叶斯公式。

假设A节点的状态有n个，即A=（a1，a2，a3…an），则根据全概率公式等到：

（1）

假设有多个节点，即U={X1，X2…Xn}，其联合概率分布式如下所示：

（2）

式中，P（ai）——节点Xi的表征节点安全状态概率。

2.2 多状态贝叶斯网节点模糊概率处理

一般地，由于数据统计不完整，多状态、多节点的贝叶斯网络节点概率是无法精确地获取的。该文主要应用解模糊语言的方法来获取节点的先验概率。

2.2.1 三角模糊数

如果用（a，b，c）表示一个三角形模糊数A，即A=（a，b，c），则其隶属度函数如下：

f（x）=（0，（x＜a）；x?a/b?a，（a≤x≤b）；c?x/c?b，（b＜x≤c）；0，（x＞c）） （3）

两个三角模糊数可以进行加减乘除等运算。

2.2.2 专家语言模糊数化

专家模糊语言与三角模糊数对应关系：非常低（0，0，0.1），低（0，0.1，0.3），偏低（0.1，0.3，0.5），中等（0.3，0.5，0.7），偏高（0.5，0.7，0.9），高（0.7，0.9，1），非常高（0.9，1，1）。

2.3 模糊安全概率测算

2.3.1 节点状态模糊概率化

将专家语言判断转化成三角模糊数。假设有n个专家，第m位专家对网络中表征节点Xi处于j状态给出判断，节点Xi处于j状态的模糊概率如下：

（4）

综合多位专家意见，最终得到一个可信度较高的模糊概率值：

（5）

2.3.2 模糊概率求解

将模糊概率转化成精确概率，得到节点Xi处于j状态的精确概率：

（6）

精确概率归一化处理：

（7）

3 实例分析

该文以广西南宁市柳南高速公路改快速路工程为研究载体，说明模型应用实用性。

3.1 节点安全概率确定

（1）节点先验概率确定。该文以驾龄节点为例，说明通过专家模糊语言判断得到节点先验概率过程。驾龄节点有三个安全状态，针对每个节点状态设置概率问卷，邀请参与工程的专家给出模糊语言评价，通过解模糊语言得到节点的先验概率，如表2所示。

应用公式（5）～（7）对专家模糊语言进行求解，得到驾龄节点三个状态的先验概率分别为P>3=0.54；P1～3=0.33；P<3=0.13。同理，通过解模糊语言得到其他节点状态的先验概率。

（2）节点条件概率确定。人员因素包含有驾龄、交通违章、安全人员配备、疲劳程度4个节点，每个节点均有3个安全状态。同样，通过解专家模糊语言确定人员、车辆、环境、管理因素的条件概率值，如表3所示。

3.2 交通安全状态评估模型

根据安全评估拓扑结构中节点之间的连接关系，将求解专家模糊语言得到的先验概率和条件概率赋值给节点，完成交通安全状态监测贝叶斯网构建，根据公式（2）实现安全概率推理。该文采用GeNIe2.0软件构建多状态贝叶斯网安全概率推理模型。

3.3 贝叶斯网交通安全状态监测模型应用

某日上午，施工单位进行高速公路中央分隔带硬化作业。施工作业区域需要占用一条车道，行车道由原来的双向四车道变为双向三车道，且导流设施设置较短，没有按规范长度设置，车辆在施工路段发生局部拥挤。当时天气为阴天，能见度一般，车流量较大，以小汽车居多。

轉化为贝叶斯网节点状态值如下：驾龄为0，违规操作为2，安全人员配备为2，疲劳程度为0，交通流为2，车型为0，车龄为0，路面平整度为1，施工作业区域为2，能见度为1，安全设施为2，安全教育情况为1，应急预案为0，安全管理制度为1。将节点安全状态带入贝叶斯网中进行概率推理，如图2所示。

安全概率推理显示安全概率为0.55，不安全概率为0.45。交通安全概率较低，易发生交通事故。人员因素、车辆因素、环境因素和管理因素安全概率分别为0.55、0.70、0.43和0.62。人员因素和环境因素不安全概率较高，说明人员因素和环境因素的安全状况正在发生恶化，可能由人员和环境恶化导致事故发生的风险正在变大。相关管理部门应及时加强施工现场管理，改善施工现场条件。

4 结语

该文构建的贝叶斯网交通安全状态评估模型，一方面能实时监测施工过程中的交通安全状态，帮助安全人员了解实时的交通安全状况，另一方面又为管理者识别施工过程中的不安全因素提供了一种技术手段。同时，交通实时安全概率值也可能对外发布，帮助交通管理部门制定交通管理措施提供决策依据。

参考文献

[1]张需鹏. 高速公路改扩建工程交通安全风险控制分析[J]. 时代农机， 2016（10）： 153-154.

[2]张翼丹. 高速公路改扩建道路设计中的安全问题探讨[J]. 江西建材， 2016（12）： 174

[3]薛冰冰. 高速公路危险路段交通安全预警系统研究[D]. 长春：吉林大学， 2013.

[4]Hernández P， Cubillo S， Torres-Blanc C. Negations on type-2 fuzzy sets[J]. Fuzzy Sets and Systems， 2014， 252： 111-124.

[5]Mkrtchyan L， Podofillini L， Dang V N. Bayesian belief networks for human reliability analysis： A review of applications and gaps[J]. Reliability Engineering & System Safety， 2015， 139： 1-16.