基于联邦学习的毫米波大规模MIMO的混合波束赋形和资源分配

孙艳华, 乔 兰, 杨睿哲, 司鹏搏, 张延华

(1.北京工业大学信息学部, 北京 100124; 2.北京工业大学先进信息网络北京实验室, 北京 100124)

随着第4代(the fourth-generation,4G)移动通信网络的普及,互联网络搜索服务、多媒体服务和应用作为现代通信的核心功能,产生了大量的数据[1]。全球部署的第5代(the fifth generation, 5G)移动通信网络旨在支持比4G更广泛的服务,并应用改进的人工智能(artificial intelligence, AI)技术,如增强现实(augmented reality,AR)、虚拟现实(virtual reality, VR)、自动驾驶等,生成了比4G多10倍的数据[2]。第6代(the sixth generation,6G)移动通信技术的钟声已经敲响,它以无处不在的AI为主要特征,不仅将产生比5G多数倍的数据,而且对数据的安全性和隐私性也有着更高的要求[3]。传统的中心式机器学习(centralized machine learning, CML)框架有着严重的隐私和安全漏洞,而且由于集中式数据的聚合和处理,带来了巨大的通信开销[4]。很显然, CML方案不再适用于今日,联邦学习(federated learning, FL)应运而生[5]。在分层FL中,边缘用户不再将原始数据发送到基站(base station, BS),而是使用本地数据进行局部模型训练,然后,将训练模型的权值或参数发送至BS。虽然边缘用户在此过程中进行了复杂的计算,但是仅发送权重或参数信息,不仅大大降低了通信开销,而且保护了数据的隐私,达到了事半功倍的效果。

大规模多输入多输出(multiple input multiple output, MIMO)技术是5G移动通信技术中提高系统容量和频谱利用率的关键技术,波束赋形技术可以利用信道状态信息将传输信号与空间信道进行匹配,将传输和接收信号的能量聚集到有限区域来提高能量利用效率和传输距离,并利用MIMO空间复用技术提高传输效率。然而,随着大规模天线的使用及信道矩阵和预编码矩阵的维数增加,导致算法复杂度、系统硬件成本和实现难度增加。

到目前为止,FL已广泛应用于物联网(Internet of things, IoT)[6]、车联网[7-8]、无人机(unmanned aerial vehicle, UAV)[9-12]等通信网络。文献[6]采用了基于FL的深度强化学习(deep reinforcement learning, DRL)方法来改进IoT环境下的卸载决策。文献[7]结合区块链和FL来解决通信开销和隐私问题,并使用DRL来选择车辆以提高效率。文献[8]提出了一种选择性模型聚合方法,通过评估局部图像质量和计算能力选择较好的局部模型发送到中心服务器。文献[9-10]利用UAV进行数据收集,并用收集的数据训练局部模型,然后,将训练后的模型发送给领头UAV,由领头UAV负责模型聚合。文献[13]比较了基于FL的3种调度策略,即随机调度、循环调度和比例公平调度,得出了在不同的应用场景下应该采取相应的调度策略,从而获取最优的系统性能。文献[14]提出了一种通信效率高的分层联合学习方法,即:将在小基站(small base station, SBS)四周具有本地数据集的移动用户分组进行FL,然后,定期将训练结果发送给SBS,由宏基站(macro base station, MBS)对SBS的训练结果进行聚合,达到全局聚合的效果。

为了降低波束赋形的难度,本文将FL应用于大规模MIMO混合波束赋形中,设计了以信道数据为输入的反向传播神经网络(back propagation neural network, BPNN)以输出相应的射频赋形矢量。同时,在边缘计算的帮助下,用户使用本地数据集进行模型训练,然后将训练后的权值和阈值发送到边缘SBS进行聚合更新。边缘服务器(edge server,ES)在满足精度要求后,将更新后的权值和阈值发送给MBS,通过相互协作,对模型进行优化。在训练过程开始之前,本文基于合同理论,设计了系统的效益函数,并通过对系统用户进行资源优化使效益函数最大。

1 模型结构

1.1 网络模型

在该框架中,假设多用户毫米波(millimeter wave,mm-Wave)MIMO的三层网络结构场景如图1所示。第1层是用户层,由N个单天线用户设备组成;第2层是ES层,包含了部署在SBS上的具有AT根天线的K个ES;第3层是云服务器(cloud server,CS)层,该层有一个部署在MBS上的单天线CS。

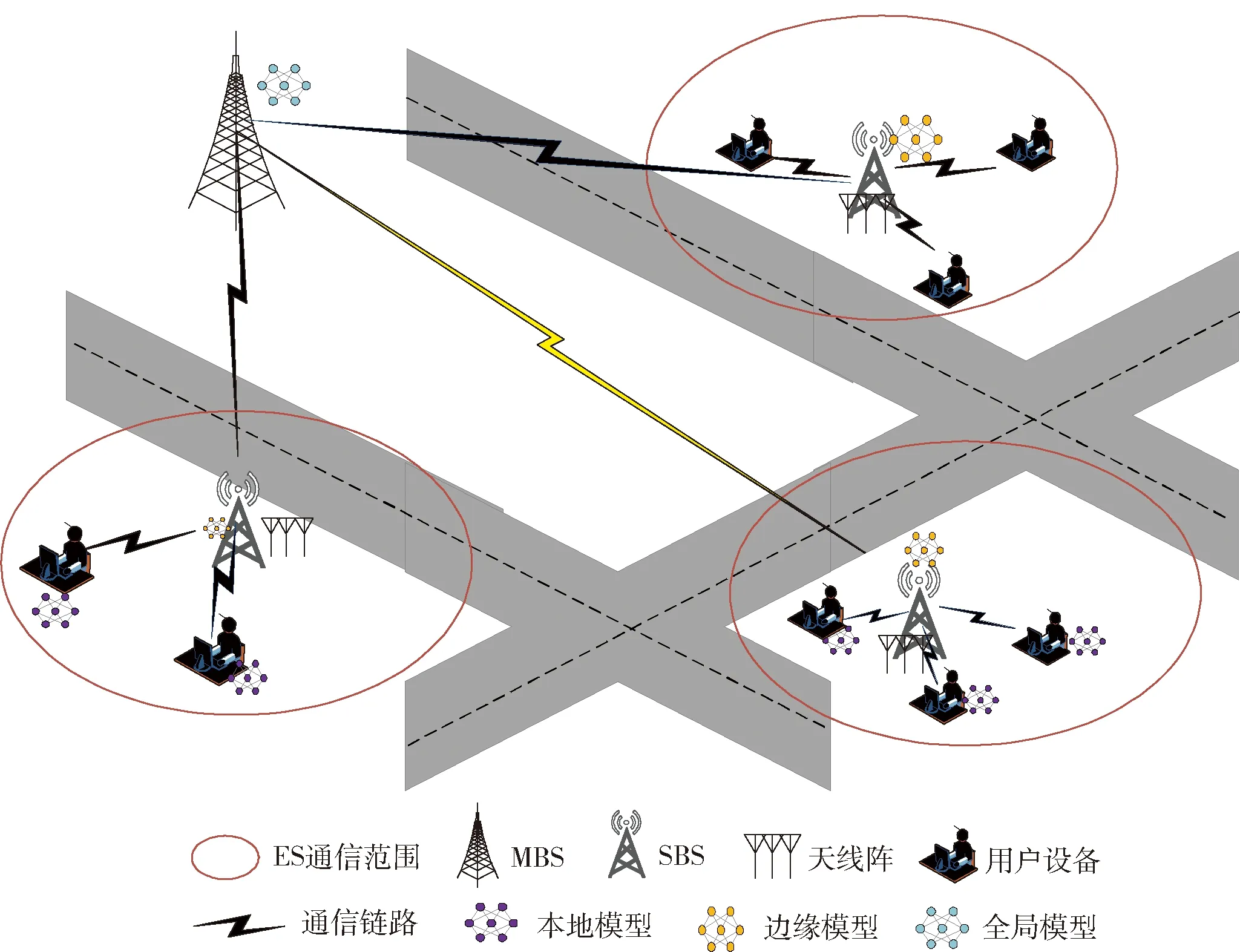
图1 三层网络结构场景Fig.1 Three-layer network architecture scenario

1.2 mm-Wave的波束赋形

在下行链路中,ES层的每个ES首先使用基带预编码器FBB=[fBB,1,…,fBB,N]∈N×N对N个发送信号s=[s1,…,sN]∈N×N进行预编码,然后,再通过使用N个射频(radio frequency, RF)预编码器FRF=[fRF,1,…,fRF,N]∈AT×N形成发送信号。假设FRF由模拟移相器组成,并且具有恒定的单模元素,即|[FRF]i,j|2=1,因此,那么,AT个发送信号可以表示为x=FRFFBBs,第n个用户接收到的信号为其中:hn∈AT为第n个用户的mm-Wave信道;zn为服从均值为0,方差为τ2的复高斯分布;zn～CN(0,τ2)为加性高斯白噪声[15-16]。

通过采用S-V(Salen-Valenzula)信道模型[17-19],hn可以表示为L个视线(line of sight, LOS)接收路径信号的叠加,即

(1)

式中:λ为波长;σ为阵列单元间距,通常设置为σ=λ/2。

在FRF的设计基础上,ES的迫零预编码可定义为

(2)

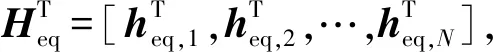
根据香农公式,第n个用户可获得的数据速率为

(3)

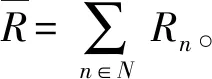
假设每个用户的本地数据集由数据输入输出对组成,即信道向量hn(输入)和对应的RF预编码fBB,n(输出),目的是通过使用用户端的本地信道数据训练出相应的模型参数w,进而得到全局模型。一旦学习阶段完成,ES可通过输入信道数据预测RF预编码,这里假设信道信息是已知的,不考虑信道估计的问题。

1.3 数据的获取

2 训练过程

在模型训练过程中,用户利用自己的本地数据训练模型来获取模型参数,然后,将模型参数传输到ES进行边缘聚合。ES对模型参数进行聚合计算后将模型参数上传到CS做最终聚合,并进行参数计算更新。最后一次更新的聚合参数将通过ES传递给用户设备,在获取更新后的参数之后用户将执行下一个迭代过程。换句话说,上述过程是一个全局迭代过程。在整个过程中,模型聚合过程包括边缘聚合和云聚合。假设每个ES的通信范围没有重叠,在通信范围内与之通信的用户集合为Sk,并且整个结构是在静态条件下进行的,用户设备在学习过程中也保持稳定。

2.1 边缘聚合阶段

2.1.1 本地模型计算

用户通过使用本地收集到的数据集,经过多次迭代后进行模型训练,迭代次数[22]为

式中:μ为常数,取决于训练任务和数据尺寸;θn定义为本地精度且θn∈(0,1),当θn→0时表示模型训练得较准确,而与之相反,当θn→1时表示经过多次迭代,模型的准确度毫无提高[23]。在用户与ES第1次通信时,ES可从用户的历史训练记录获得用户的训练精度θn。

在这个过程中,用户n产生的计算延迟可表示为

(4)

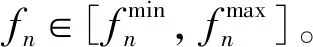
用户n在经过L(θn)的本地迭代之后所消耗的能量为

(5)

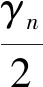
2.1.2 本地模型传输

在完成L(θn)本地迭代之后,每个用户将计算得到的模型参数wn发送到与之通信的第k个ES,k∈K,因此,在传输过程引起了通信延迟和能量消耗。在本文中,假设用户采用正交频分多址接入(orthogonal frequency-division multiple access, OFDMA)ES,第k个ES提供总带宽Bk给服务用户。定义βk,n是分配给用户的带宽占比,每个用户分得的带宽可以表示为βk,nBk,那么用户n可获得的传输速率rn为

(6)

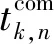
(7)

则在这个过程中用户n的能量消耗为

(8)

2.1.3 边缘模型聚集

在这个步骤中,每个ES从与之通信的用户处收集更新的模型参数,通过计算

(9)

得到边缘模型参数wk。

之后,第k个ES向Sk中的用户设备广播wk,用户设备使用wk进行下一轮本地模型计算,直到第k个ES达到精度ε[25],在本文中假设所有ES有相同的精度。为了达到所需的模型精度,边缘迭代次数表示为

(10)

在本文中,不考虑边缘模型聚合及广播至用户所消耗的时间和能量。同时,因为用户设备接收边缘聚合模型参数wk的时间和能量开销比上传本地模型参数wn小,所以这部分也忽略不计。因此,当进行I(ε,θn)次边缘迭代后,用户设备n的总能量消耗为

(11)

同样,第k个ES达到边缘精度ε时,消耗的时间可推导为

(12)

2.2 云聚合阶段

2.2.1 边缘模型上传

每个ES在I(ε,θn)边缘聚合后上传wk到CS进行全局聚合。设rk是第k个ES将模型参数上传至CS的传输速率,公式为

(13)

式中:BC为CS提供的带宽且不同ES的带宽相等;l为ES和CS之间的距离(忽略小尺度衰落);l为信道的衰减因子。因此,第k个ES上传模型参数的时延和消耗能量分别为

(14)

(15)

式中dk为第k个ES模型参数的数据大小。

2.2.2 云模型聚合

边缘模型参数上传后,CS将所有ES接收到的模型进行聚合,可得总模型参数为

(16)

3 资源分配

3.1 基于合同理论的资源分配方案

(17)

根据合同理论,每个合同项必须满足2个约束,即满足个体合理性(individual rationality, IR)约束和激励相容性(incentive compatibility, IC)约束,以保证充分调动参与FL的每类用户。

定义1 IR约束每个用户应根据计算效益函数选择适合的合同条款以实现非负效益,即

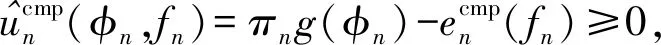
(18)

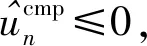
定义2 IC约束为了最大化效益,每个用户设备n只能选择为自己设计的合同条款(fn,φn),可以表示为

(19)

3.2 系统效益函数

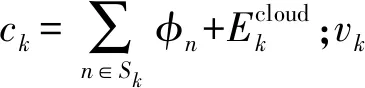
(20)

综上,系统基于合同理论的资源优化目标函数可表示为

C3: 0≤βk,n≤1,∀n∈Sk,∀k∈K;

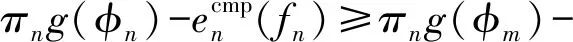
(21)

式中:C1和C2分别表示上行通信资源约束和计算能力约束;C3表示每个用户带宽占比为[0,1];C4和C5分别是合同理论的IR约束和IC约束。

3.3 基于效益函数的优化资源分配

为了简化表示,优化方程的一部分可表示为

(22)

(23)

(24)

Cn=L(θn)bnρnDn

(25)

(26)

式中Jn、Mn、Qn、Cn和Gn是常数,与用户设备n的参数和系统设置相关。

优化问题(21)由于受到C4和C5的约束而难以求解,由文献[28]可得

(27)

(28)

综上,式(21)可表示为

C3: 0≤βk,n≤1,∀n∈Sk,∀k∈K;

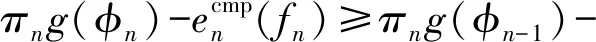
(29)

由于g(φn)随着奖励φn的增加而增加,为了量化分析,设g(fn)=ζfn,ζ为常系数,一般地ζ≠1,由约束C4和C5可分别解得

(30)

(31)

结合式(30)(31)可得

(32)

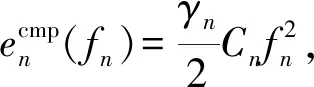
(33)

最终优化目标函数可表示为

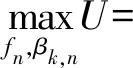
C3: 0≤βk,n≤1,∀n∈Sk,∀k∈K;

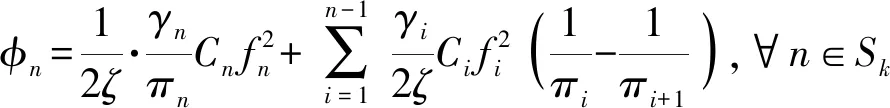
(34)

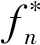
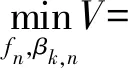
C3: 0≤βk,n≤1,∀n∈Sk,∀k∈K;

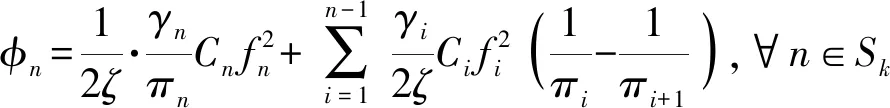
(35)

4 仿真结果及分析

4.1 仿真参数设置

假设SBS部署了3个ES,分别为K1、K2、K3,每个服务器有100根天线。将整个数据集随机分为80%和20%,分别进行训练和测试,其中80%的训练集又被随机分为70%、15%和15%用来支持BPNN的模型训练、验证和测试。其他相关仿真参数见表1。

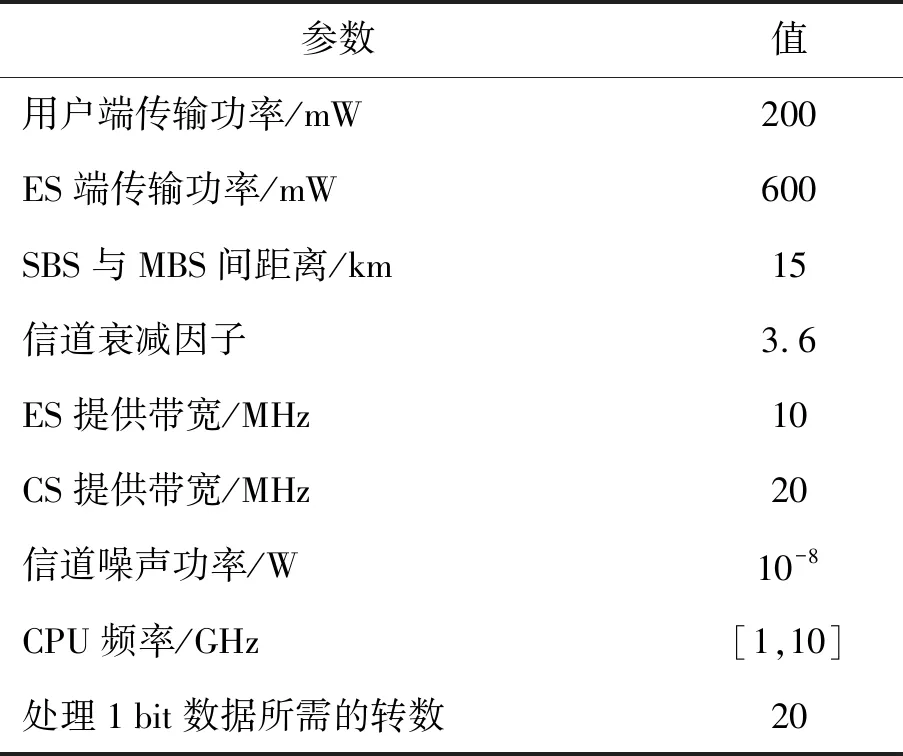
表1 仿真参数设置

4.2 仿真结果及分析

设置每个服务器的通信范围内分别有N={5,8,7}个用户且所有ES通信范围内的用户精度相同。在整个过程中,每个服务器的通信范围内用户个数不变,用户的频率f和带宽占比β在不同精度下保持一致。ES精度ε=0.2,边缘用户精度分别设置为0.1、0.3、0.5、0.7、0.9。

不同精度的用户资源消耗情况如图2、3所示。随着用户精度的增大,时延减小,能耗增大。这是因为训练精度高的用户需要更多的本地迭代,导致延迟增加,而低精度用户的本地迭代次数较少,这就意味着与服务器的通信次数增多,从而导致能量的消耗增加。

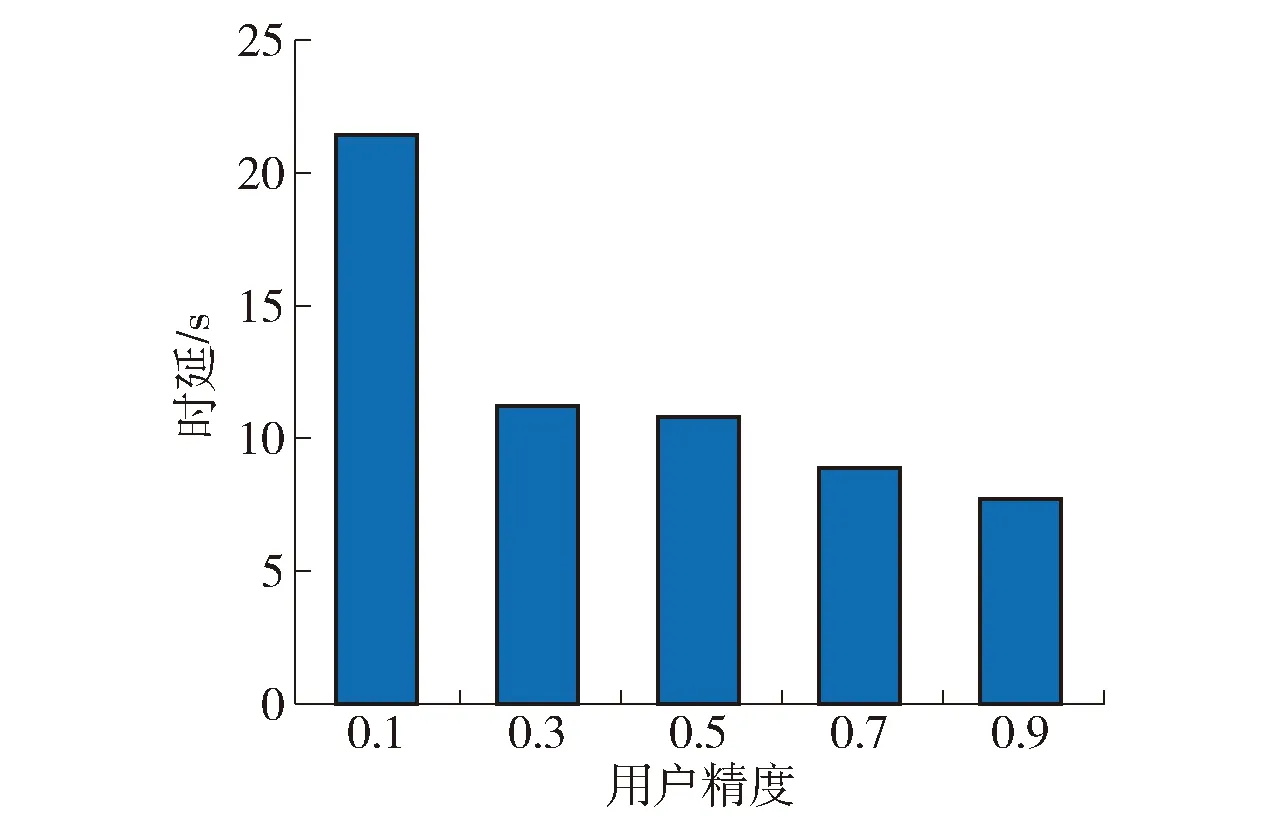
图2 不同用户精度对系统时延的影响Fig.2 Influence of different user precision on system latency

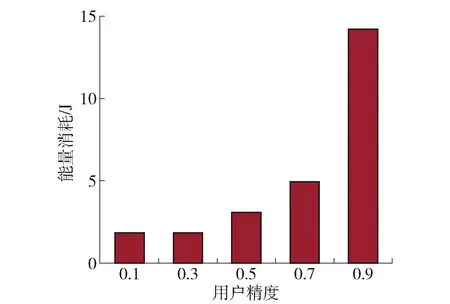
图3 不同用户精度对系统能量消耗的影响Fig.3 Influence of different user accuracy on system energy consumption

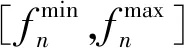
如图4～6 所示,K1、K2、K3经过优化求解器迭代计算后系统效益达到图6所示目标函数值最小(系统效益最大)时,3个ES通信范围内资源分配后用户频率和带宽占比变化情况。由图4、5可得,在每个用户分配近似的频率和相同带宽的情况下,系统达到最好的状态且资源消耗最少。

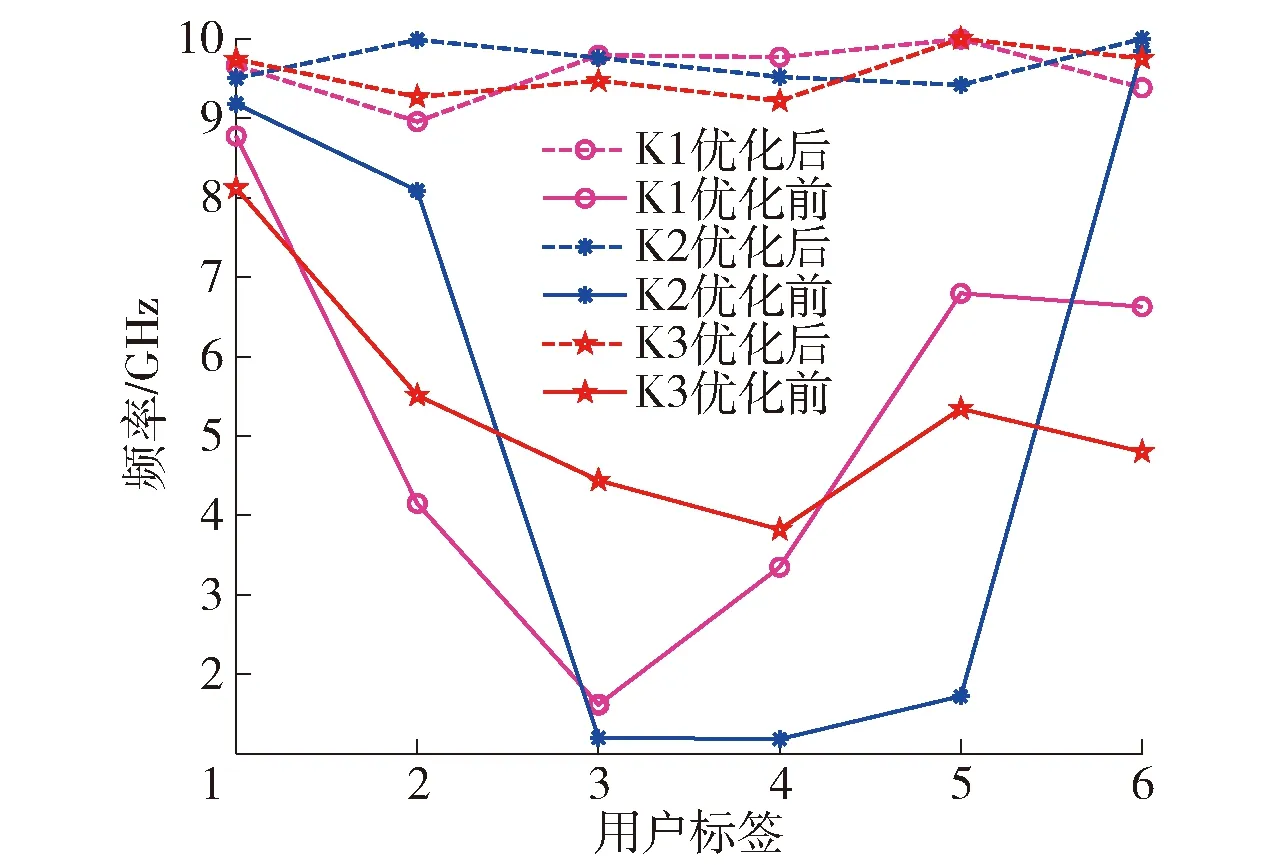
图4 资源分配后用户频率变化Fig.4 User frequency changing after resource allocation

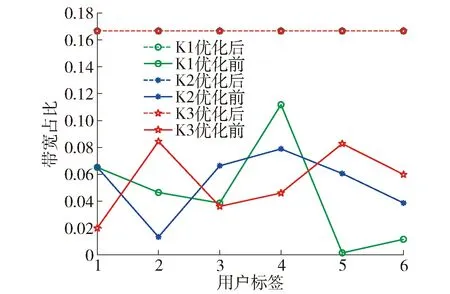
图5 资源分配后用户带宽占比变化Fig.5 Changes in the proportion of user bandwidth after resource allocation

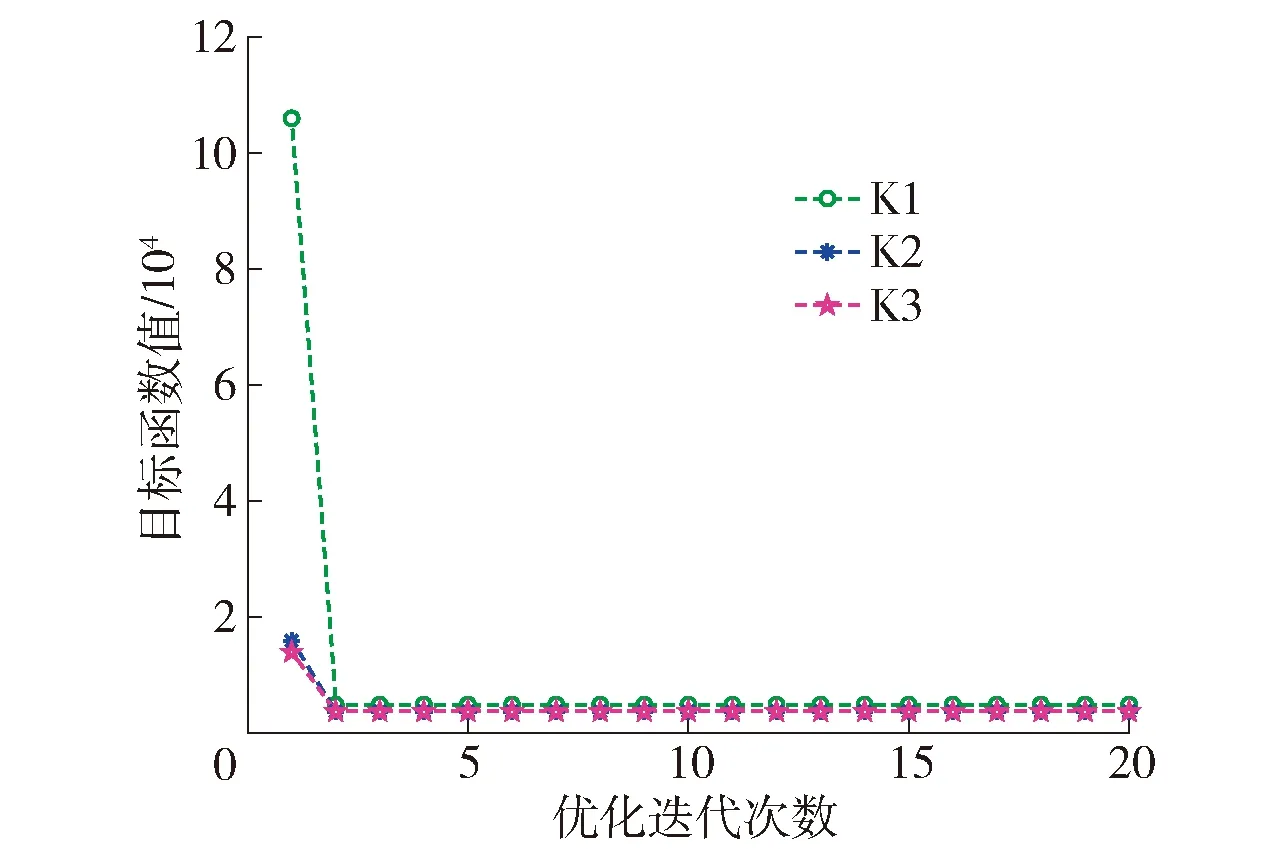
图6 系统效益随优化迭代次数的变化Fig.6 System benefit changing with the number of optimization iterations

如图7、8所示,资源优化分配前后系统时延和能量消耗情况,资源分配后无论是时间还是能量的消耗有了明显的减少,因此,充分体现出对系统资源进行优化分配的重要性。

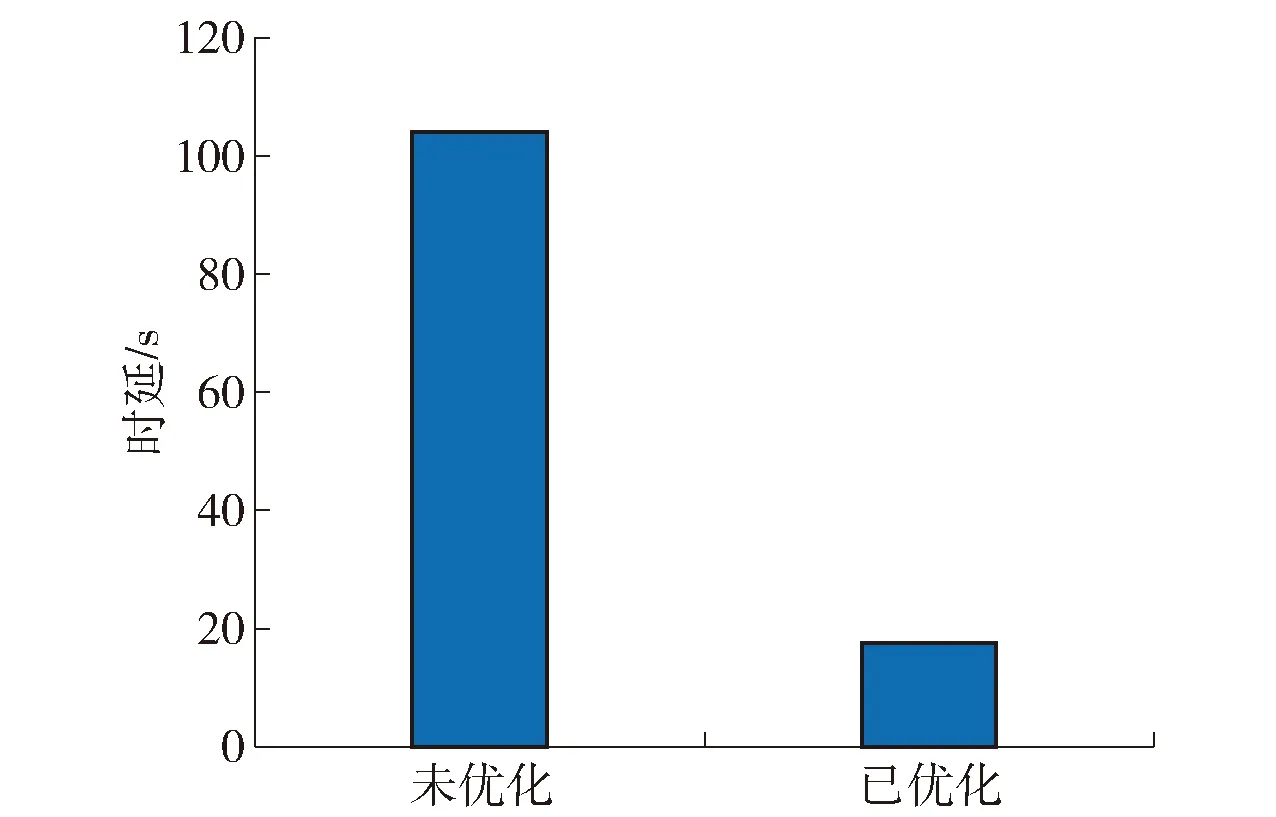
图7 优化前后系统时延Fig.7 System latency before and after optimization

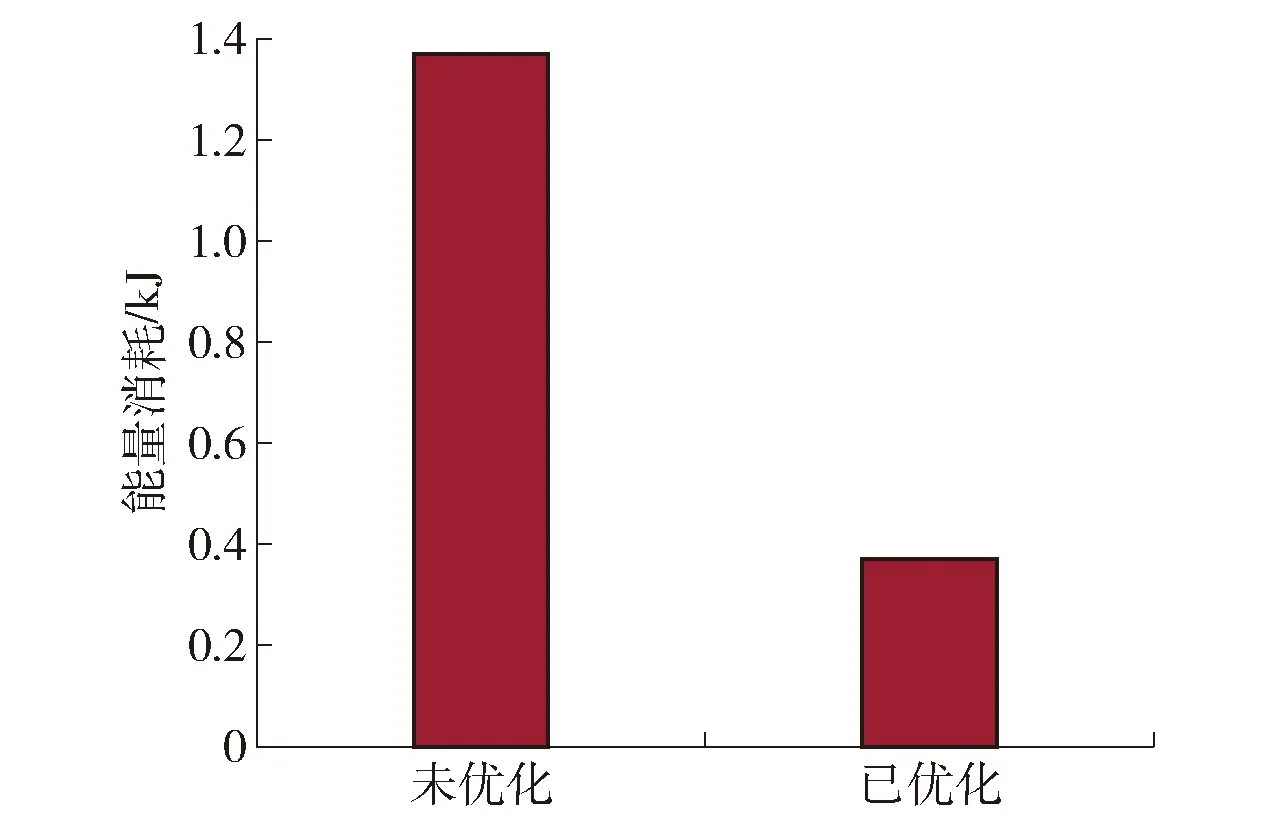
图8 优化前后系统能量消耗Fig.8 System energy consumption before and after optimization

图9～12显示了BPNN对非线性数据处理的性能。设置在每个服务器的通信范围内有N={4,6,8}个用户,并且在整个过程中,每个服务器的通信范围内用户及其个数不变。

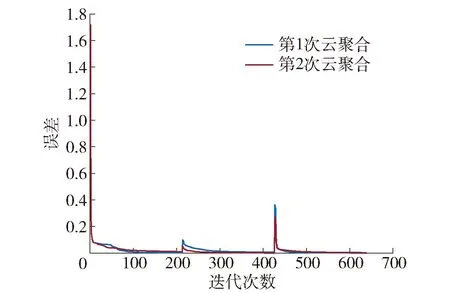
图9 用户损失误差值随迭代次数的变化Fig.9 User loss error value changing with the number of iterations

图9显示的是在进行2次云聚合过程中一个用户的训练损失误差随迭代次数的变化情况。可以看出,用户训练的损失误差收敛速度不仅快且接近于0。边缘聚合后,损失误差稍有反弹,这是由于用户精度不同,训练的准确度有差异,但是训练误差在聚合时被平均分到每个用户。在第2次云聚合后,反弹程度降低,性能有所增加。

图10显示的是其中一个用户在模型训练过程中数据拟合程度。从图中可以看出,整个训练总体达到0.972 95。如图11所示,测试相应用户数据集中的200个样本,将预测输出和期望输出进行比较,结果表明90%以上样本可完美预测,进一步验证了模型训练的准确度。

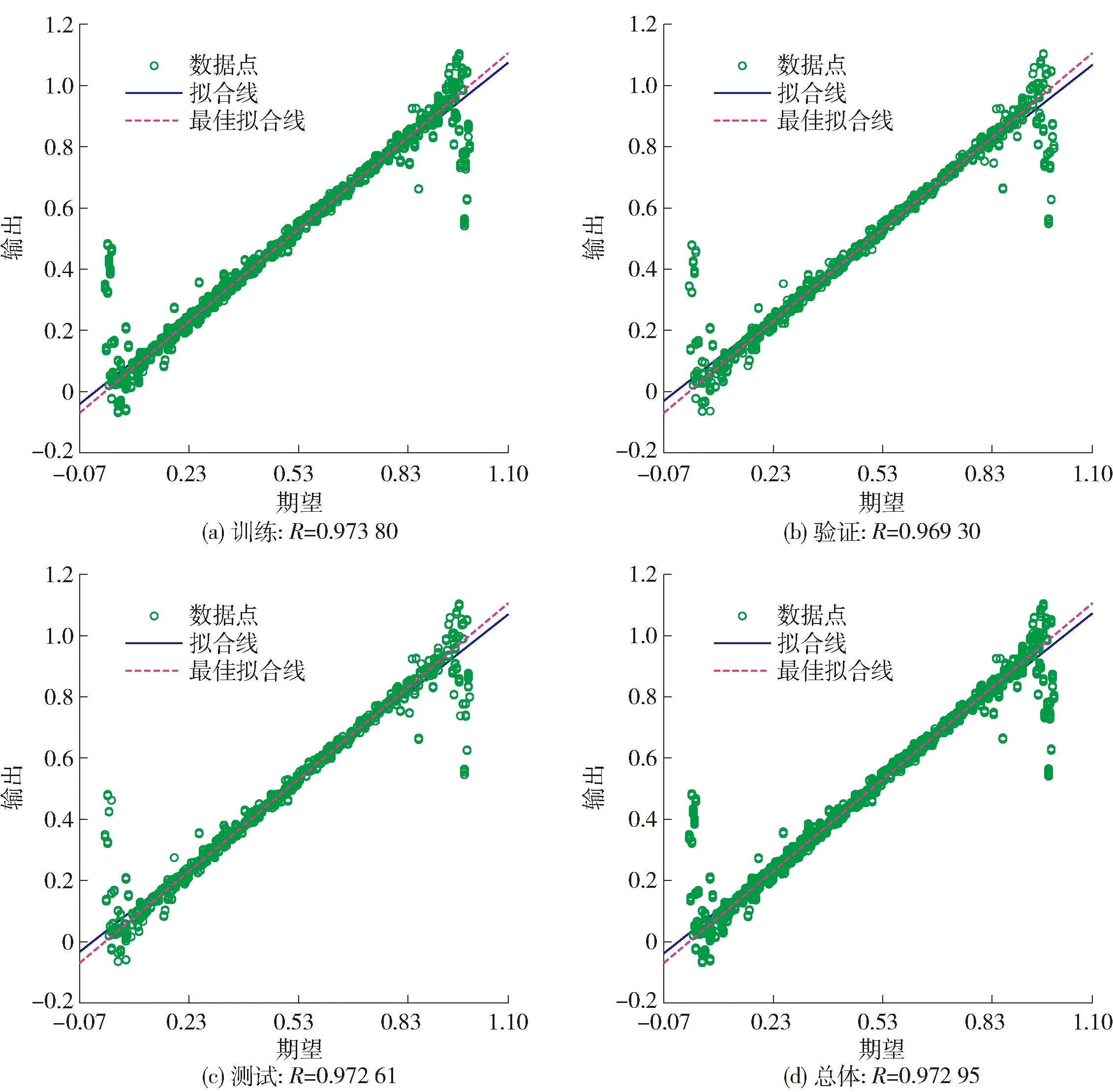
图10 BPNN训练、验证和测试阶段拟合情况Fig.10 Fitting of BPNN training, verification and testing phases

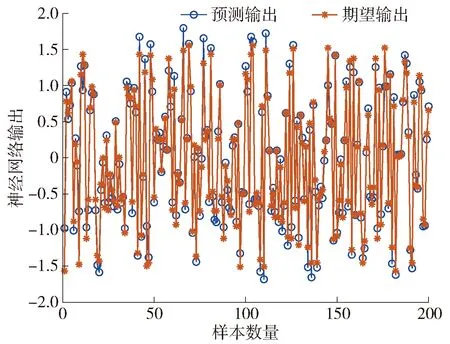
图11 BPNN预测输出结果Fig.11 BPNN predicted output result

如图12所示,比较了不同SNR下的基于FL、CML、正交匹配追踪(orthogonal matching pursuit,OMP)[29]和全数字波束赋形和速率的变化。由图可得:

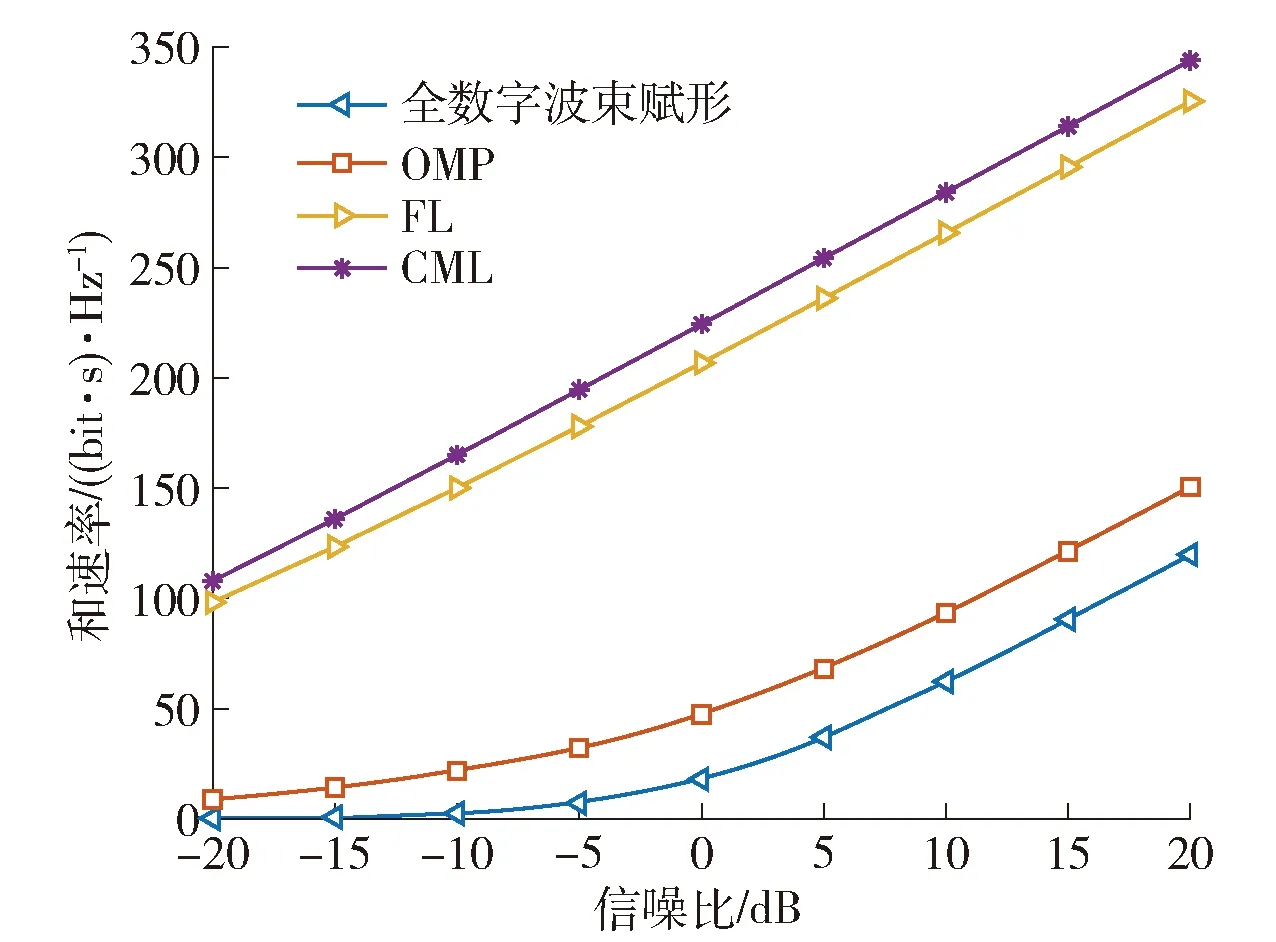
图12 不同SNR下的和速率Fig.12 Sum rate with different SNR

1) 基于FL和CML方法的和速率要远远大于基于OMP的混合波束赋形和全数字波束赋形的和速率,这也证明了本文将机器学习与波束赋形结合方法的可行性,不仅简化了算法而且还可以获得更高的性能。

2) 基于FL的方法取得了与CML近似的和速率,在保证通信性能的基础上减少了通信开销。CML的性能比FL稍好一些,这是因为CML获得了全部数据集,而FL采用的是分布式学习方法。

5 结论

1) 用户精度对于系统资源消耗具有巨大影响,用户精度高所需本地模型训练迭代次数多,计算时间增加;精度降低,本地训练次数减少,通信次数增加,能耗增加。

2) 提出了基于合同原理的激励和资源分配方案。资源优化分配前后资源消耗大大降低,缓解了FL对于资源受限的困扰。

3) 将混合波束赋形技术应用于BPNN,通过仿真验证了BPNN对混合波束赋形具有极高的性能,利用BPNN减轻了混合波束赋形技术的困难程度,降低了对信道信息的敏感性。同时,通过与CML的和速率进行比较,验证了所提出的网络架构可以达到与其几乎相同的性能,并且要比其他波束赋形方案性能更好。