金氰化浸出过程混合建模及仿真算法分析研究
2023-08-05莫文水
莫文水
(广西现代职业技术学院,广西 河池 547000)
目前,湿法冶金浸出过程反应模型通常依据物料守恒、能量守恒及动力学方程建立[1-5],但大部分研究依据理论仿真得出结论,与实际生产情况有偏差,试验参数无法固定,很难准确获取数据,易导致研究结论与实际生产情况不相符[6-12]。
针对某金氰化浸出过程金浸出率无法精准预测的问题,首先建立了单级浸出动态模型,再基于单级模型建立多级浸出动态模型,并仿真验证多级浸出动态模型浸出率的变化趋势;其次用基于免疫原理的RBF神经网络数据模型的学习算法模拟动力学反应速度方程,估算动态机制模型中的未知参数,与物料守恒方程串联,建立了浸出率预测的串联混合模型,并根据模型的预测误差进行模型更新;最后通过在实际工业生产中的应用,验证串联混合模型的准确性。
1 动态模型的建立
1.1 单级和多级浸出动态模型的建立
某金浸出工艺选择气力连续搅拌槽反应器(CSTR)[13]为浸出槽,以NaCN溶液作浸出剂,采用多级串联方式进行氰化浸出。提前假设搅拌槽内温度分布均匀、矿浆搅拌均匀、反应过程中不放热、忽略反应器中的物料隔离且浸出槽中矿浆pH恒定[8,13-14]。
根据金氰化浸出过程的物料守恒和动力学反应,建立单级动态模型[12]。物料守恒方程如下:
固相金守恒方程,
(1)
液相金守恒方程,
(2)
液相氰守恒方程,
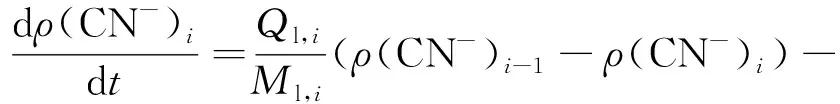
(3)
式中:i—浸出槽级数;ws,i—固相金品位,mg/kg;wl,i—液相金品位,mg/kg;ρ(CN-)i—液相氰根离子质量浓度,mg/L;Qs,i—矿浆固相流量,kg/h;Ql,i—矿浆液相流量,kg/h;Q(CN-)i—浸出槽中添加的氰化钠流量,mg/h;Ms,i—浸出槽中固相滞留质量,kg;Ml,i—浸出槽中液相滞留质量,kg;r(Au)i—金溶解速度,mg/(kg·h);r(CN-)i—氰离子的消耗速度,mg/(kg·h)。
将动力学反应方程[14]与实际样本数据相结合,采用最小二乘法计算模型[15]参数:
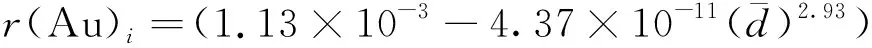
(4)
(5)
(6)
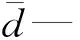
假设浸出过程稳定,基于Qs,i和Ql,i质量守恒可知:
Qs,i=Qs,i-1;
(7)
Ql,i=Ql,i-1。
(8)
假设浸出槽中所有反应物充分混合,Qs,i和Ql,i之间的转化关系式为:
(9)
式中:ρw,i—矿浆浓度,kg/L。忽略物料隔离,假设Qs,i和Ql,i与矿浆有相同的τi:
(10)
式中:ρs—矿浆中固相密度,g/cm3;ρl—矿浆中液相密度,g/cm3。
由式(9)、(10)分别得固相、液相滞留量为:
Ms,i=Qs,i×τi;
(11)
Ml,i=Ql,i×τi。
(12)
综上,式(1)~(12)组成了单级浸出动态模型。
使用ODE45计算该动态模型得到ws,i,再由式(13)计算金浸出率:
(13)
基于单级浸出动态模型,将串联的每一级浸出槽的输出变量作为下一级浸出槽的输入变量,建立多级浸出动态机制模型,从而得到每一级浸出槽中矿浆的固相金品位,之后由式(14)计算整个浸出过程金总浸出率:
(14)
式中:ws,0—矿浆初始固相金品位,mg/kg;ws,N—N级浸出后矿浆的固相金品位,mg/kg。
1.2 多级浸出动态模型的仿真分析
采用六级浸出槽的浸出率试验数据对多级浸出动态模型进行模拟,并仿真分析不同输入变量对浸出率变化趋势的影响[14-16]。模型中相关变量取值见表1。
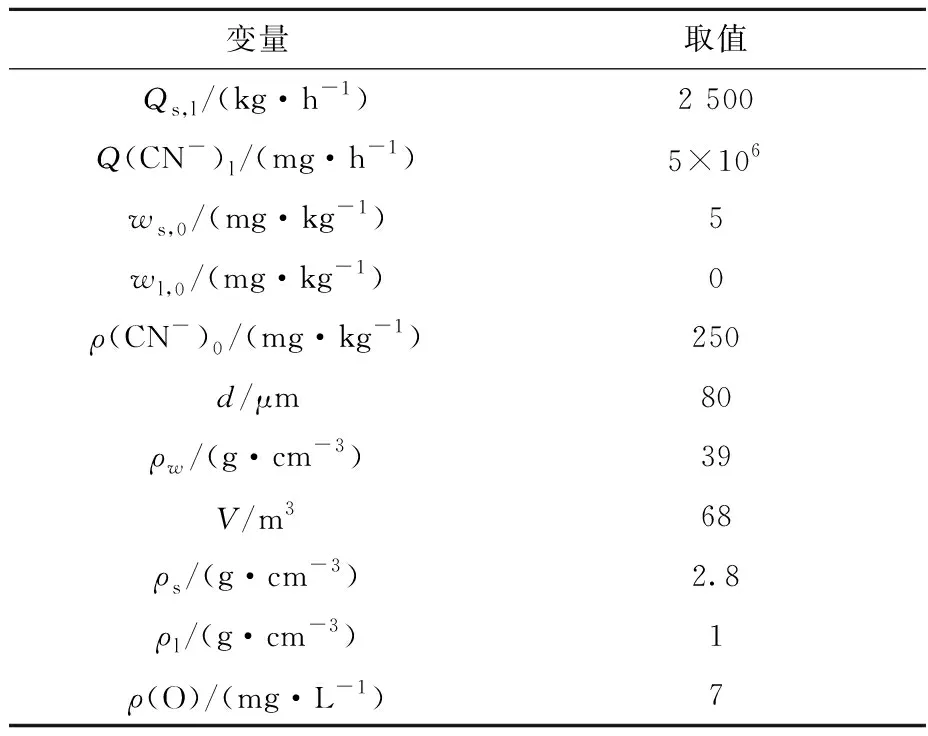
表1 多级浸出动态模型中相关变量取值
分别以矿石流量、矿浆质量浓度、氰化钠添加流量、溶解氧质量浓度及矿石平均粒径为输入变量,其余变量按照表1取值,仿真分析5个变量对金浸出率的影响,试验结果如图1~5所示。
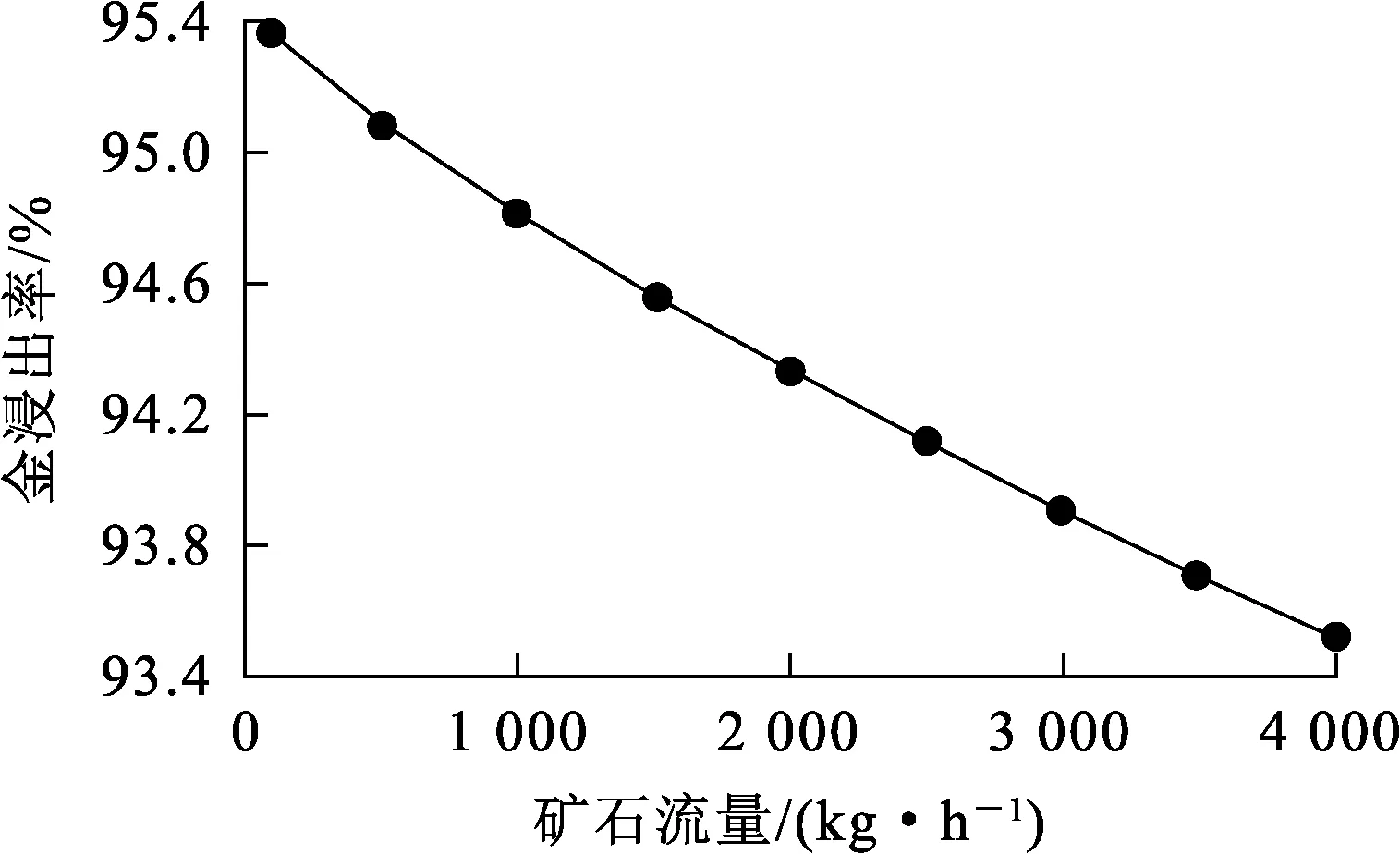
图1 矿石流量对金浸出率的影响
由图1看出:金浸出率随矿石流量增大而降低。因为矿石流量增大易导致矿浆在浸出槽中滞留时间变短,使矿浆无法与浸出剂充分反应,造成金浸出率降低。由图2看出:金浸出率随矿浆质量浓度增大而提高,矿浆质量浓度增至20 kg/L后,金浸出率趋于稳定。这是由于矿浆质量浓度过大,黏度增大,导致金浸出不完全。由图3看出:金浸出率随氰化钠添加流量增加先快速升高;氰化钠添加流量增至50 mg/h后,金浸出率升高幅度趋缓慢。由图4看出:金浸出率随溶解氧质量浓度增加而提高,溶解氧质量浓度增至5 mg/L以后,金浸出率的增长幅度趋缓。由图5看出:浸出率随矿石平均粒径增大而降低。矿石平均粒径增大会导致化学反应不充分,使得浸出率减小。通过以上对动态机制模型中各输入变量对浸出率影响的仿真分析,帮助我们更好的分析了浸出率的影响因素情况及动态特性,为实际生产过程提供正确的理论指导。
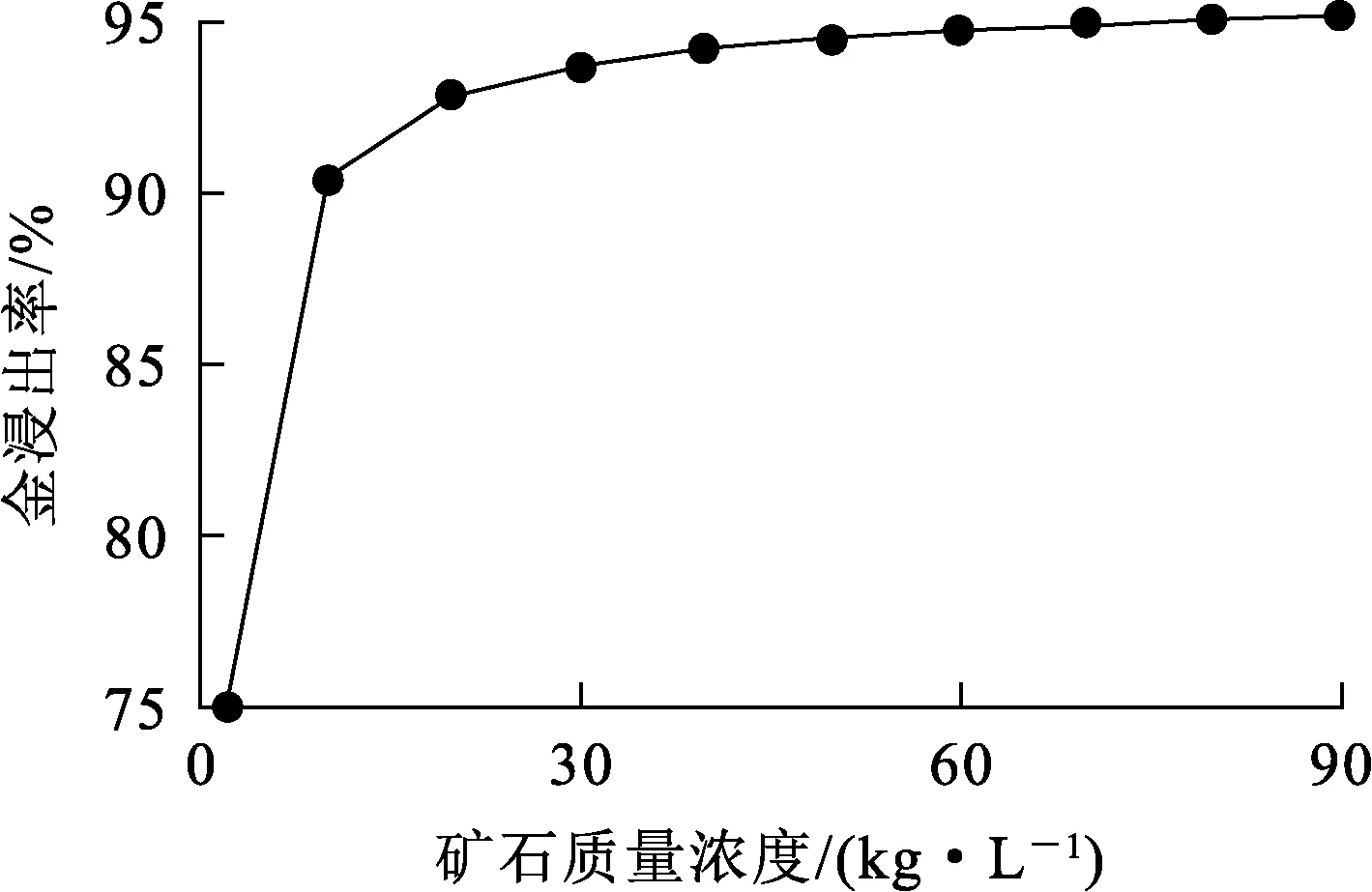
图2 矿浆质量浓度对金浸出率的影响
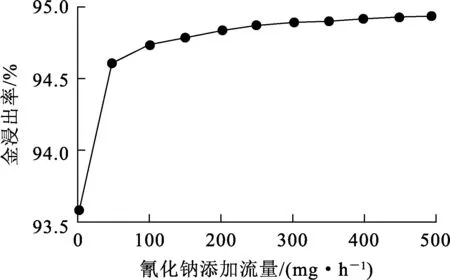
图3 氰化钠添加流量对金浸出率的影响
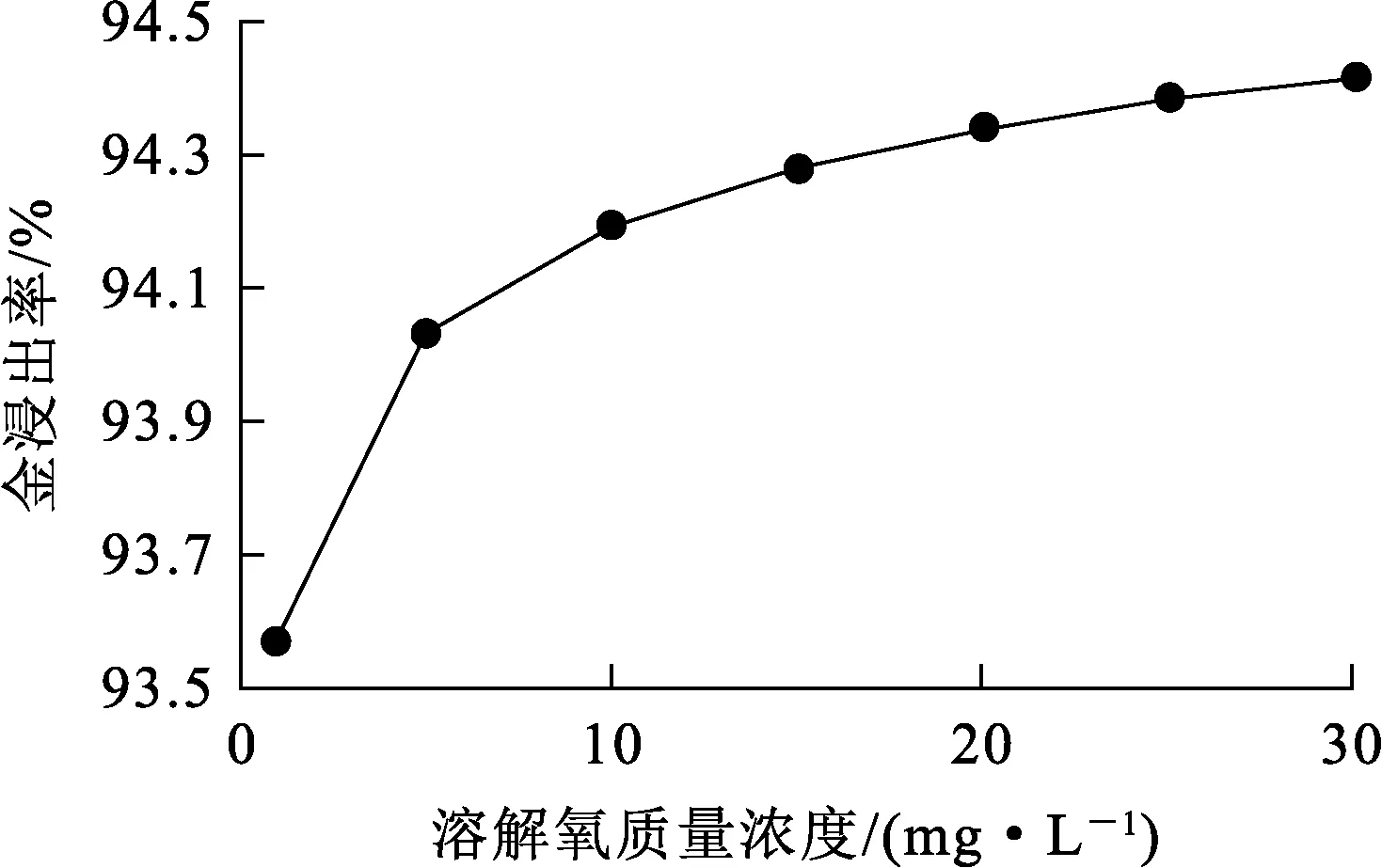
图4 溶解氧质量浓度对金浸出率的影响
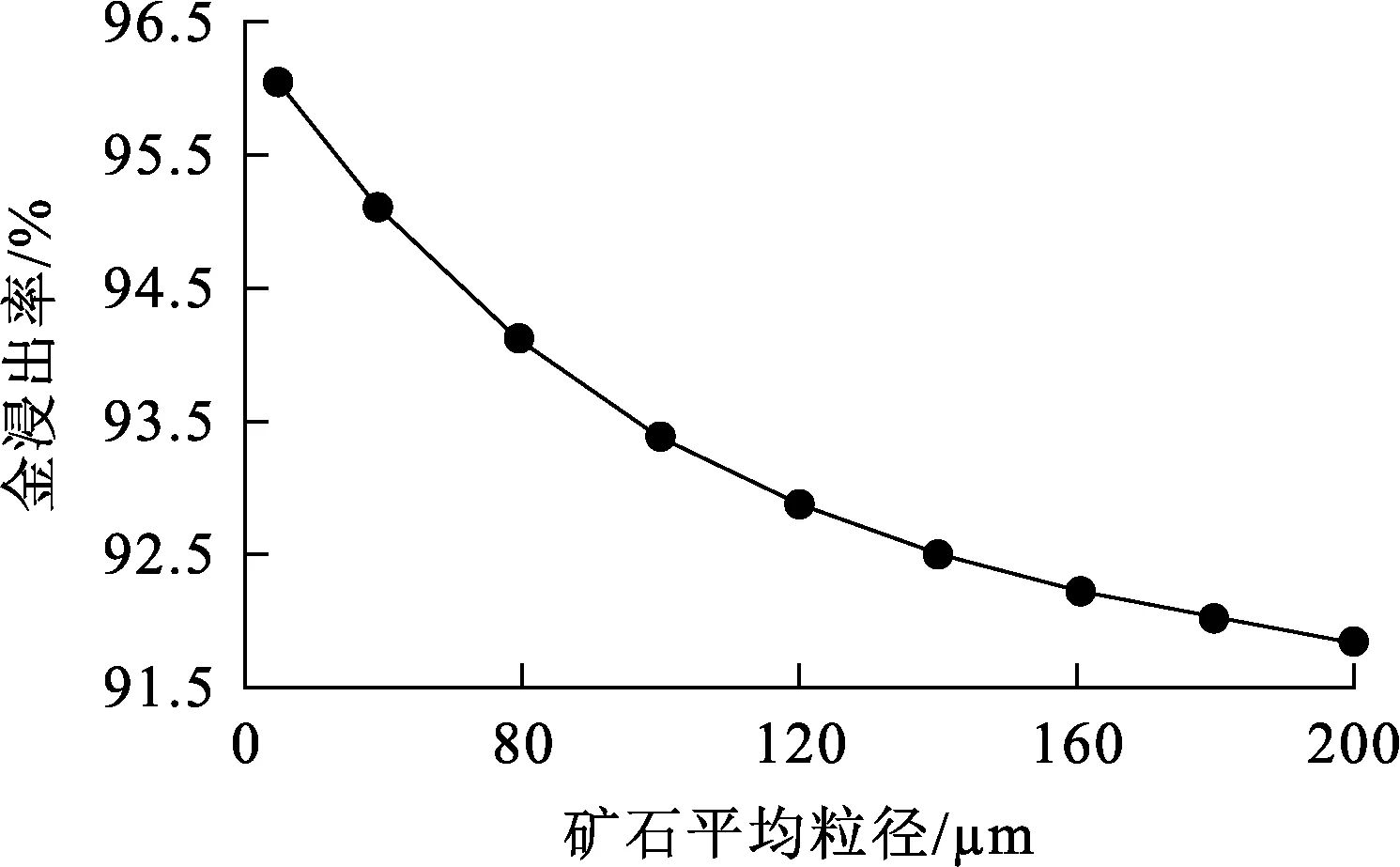
图5 矿石平均粒径对金浸出率的影响
2 基于RBF神经网络的串联混合模型
实际浸出过程中,动力学反应速度无法直接测量,因此,以浸出过程动态模型为基础,采用径向基函数神经网络(RBFNN)数据建模法[17-21]建立浸出过程的动力学反应速度模型,估算浸出过程动态模型中的未知参数,再与物料守恒方程串联,从而建立预测浸出率的串联混合模型。
2.1 径向基函数神经网络
RBF神经网络是一种具有单隐层的三层前馈网络,包括输入层、隐含层和输出层。本研究主要讨论神经网络的训练算法,包括基础设置与公式。
设输入层、隐含层、输出层的节点数分别为n、m、s,有N组输入输出样本对应(X(i),Y(i),(i=1,2,…,N)),其中X(i)是n维向量,Y(i)是s维向量,输入层连接隐含层的权值设为1,n维径向基函数则作为隐含层节点的激活函数:
(15)
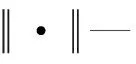
径向基函数通常选取Gaussion函数:
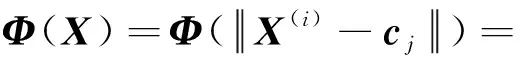
(16)
式中,σj—第j个以cj为中心的高斯函数宽的向量。
一般输出可表示为:
(17)
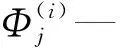
式(17)的矩阵形式为:
Y=ΦW,Φ∈RP×(m+1),W∈R(m+1)×s。
(18)
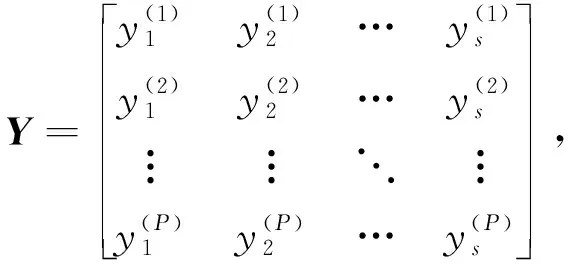
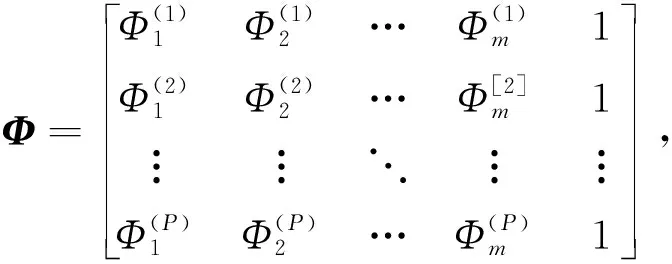
RBF神经网络算法是目前常用的混合学习算法之一,主要包含两个阶段。
第一阶段是非监督学习阶段,需要得出径向基函数中的数据中心和宽度,通常采用K-means聚类算法。首先定义参数:P个样本{X1,X2,…,XP},M个隐节点数,c(k)是第k次迭代的中心。其次随机确定M个互不相同的向量c1(0),c2(0),…,cM(0)作为初始聚类中心;随后计算输入样本点与选择的聚类中心点的欧式距离并比较得出距离最小值的节点:
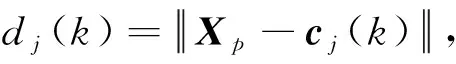
(19)
令r表示该隐含层节点下标,根据式(20)与聚类中心的最小欧几里得距离对每一个输入样本Xp进行归类:
(20)
式中:r(Xp)—Xp被分为r类。
同理将所有样本分为M个子集U1(k),U2(k),…,UM(k),代表M个聚类域。采用竞争学习的规则对各个聚类中心进行调整:
(21)
式中:η—学习率,取值范围为[0,1]。
其次,令k=k+1,判断c的改变量是否小于预设阈值,是则利用聚类中心之间的距离确定径向基函数的扩展常数;否则通过式(19)重新计算欧氏距离并寻找距离最小值的隐含层节点,并按照以上步骤继续计算直至c的改变量小于预设阈值。
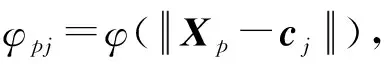
混合学习算法虽有一定优点,但也存在RBF神经网络的隐含层数需要提前根据试验确定,其数值的不同会很大程度影响聚类的性能等缺点。
2.2 基于免疫原理的RBF神经网络模型学习算法
针对混合学习算法存在的不足,研究人员提出了免疫网络模型[12],改进后可用于选择RBF神经网络隐含层数据中心(隐含层数),无需提前试验确定。
假设一组向量作为输入数据X={x1,x2,…,xN},其中向量xi=[xi1,xi2,…,xip]T∈Rp(i=1,2,…,N)。确定RBF神经网络的数据中心需得到一个新的数据集作为聚类的输入数据,设该数据集为C={c1,c2,…,ch},cj=[c1j,c2j,…,cpj]T∈Rp,j=1,2,…,h,其中h远小于N。
首先定义抗原与抗体间的相互作用强度为亲和力,设输入数据xi和数据中心cj之间的亲和力为aij;定义抗体与抗体间的相互作用强度为相似度,设数据中心ci与数据中心cj之间的相似度为sij;其中aij与sij的表达式分别为:
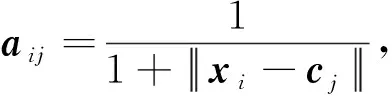
(22)
(23)
改进后的免疫网络模型算法[12]如下:
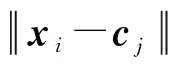
(24)
式中:ak—抗体ck的亲和力,ak越高,突变率越低。
2)数据中心集突变后,重新计算xi与L’中Nc个数据中心的亲和力,并选取ξ%个亲和力最大的数据中心,生成数据中心记忆集m。设定阈值σd,消除m中亲和力比σd小的数据中心,生成新的数据中心记忆集m’。为了清除突变集中相互识别的数据中心防止产生抑制,设定阈值σs,计算m’中各数据中心间的相似度sij,并比较sij与σs;若sij>σs,保留该数据中心,反之则清除。
3)将全部数据中心记忆集m’合并生成总数据集M。计算M中所有数据中心间的相似度sij,同理利用sij>σs清除不同数据集中相似的数据中心,完成免疫系统中的网络抑制过程,生成最终数据集M’。
4)最后,随机选取一定数量的新数据中心替换C中对应数量亲和力低的数据中心,重复以上步骤。达到预设的最大递推次数后的M’即为所求的RBF数据中心集。
综上,即可确定RBF神经网络的隐含层数。随后,采用递推最小二乘法求解线性方程组Y=ΦW中的W,即可估计输出层权值。计算P(k):
(25)
式中:P(k)—逆相关矩阵;Z(k)—隐含层节点的输出值;λ—遗忘因子,一般取0<λ<1。
更新网络权值:
W(k)=W(k-1)+g(k)[y(k)-ZT(k)W(k-1)]。
(26)
式中:W(k)—权值矢量;y(k)—神经网络的期望输出。
给出终止条件:
(27)
式中:J(k)—误差;ε—误差满足的迭代停止值。若|J(k)-J(k-1)|<ε,则此时的W为最终值;反之,转到计算P(k)值继续迭代。由此,确定了输出层的权值。
2.3 仿真分析
基于某金精炼厂浸出工艺采样数据,对串联混合模型进行仿真验证。为了方便对比分析,建立一个基于免疫原理RBF神经网络的纯数据模型(RBFNN数据模型)。将输入与输出数据之间拟合成非线性函数关系,模型的方程式如下:
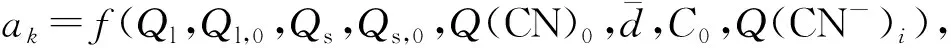
(28)
对串联混合模型仿真验证的变量取值参见表1,免疫学习算法中RBFNN数据模型参数取值见表2。
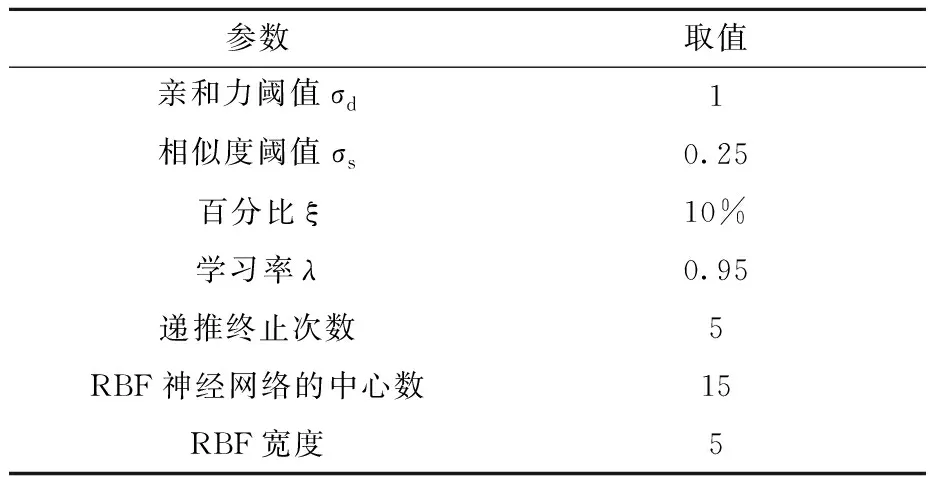
表2 免疫学习算法中RBFNN数据模型参数取值
两种模型预测效果的评价指标如下:
1)最大绝对误差(MAE)
(29)
2)均方根误差(RMSE)
(30)
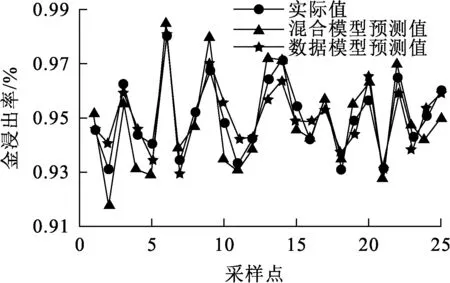
选择200组数据作为样本集,仿真分析浸出过程金浸出率的动态变化过程;再选取25组浸出达到稳态后的数据作为样本进行验证,结果如图6、7所示。
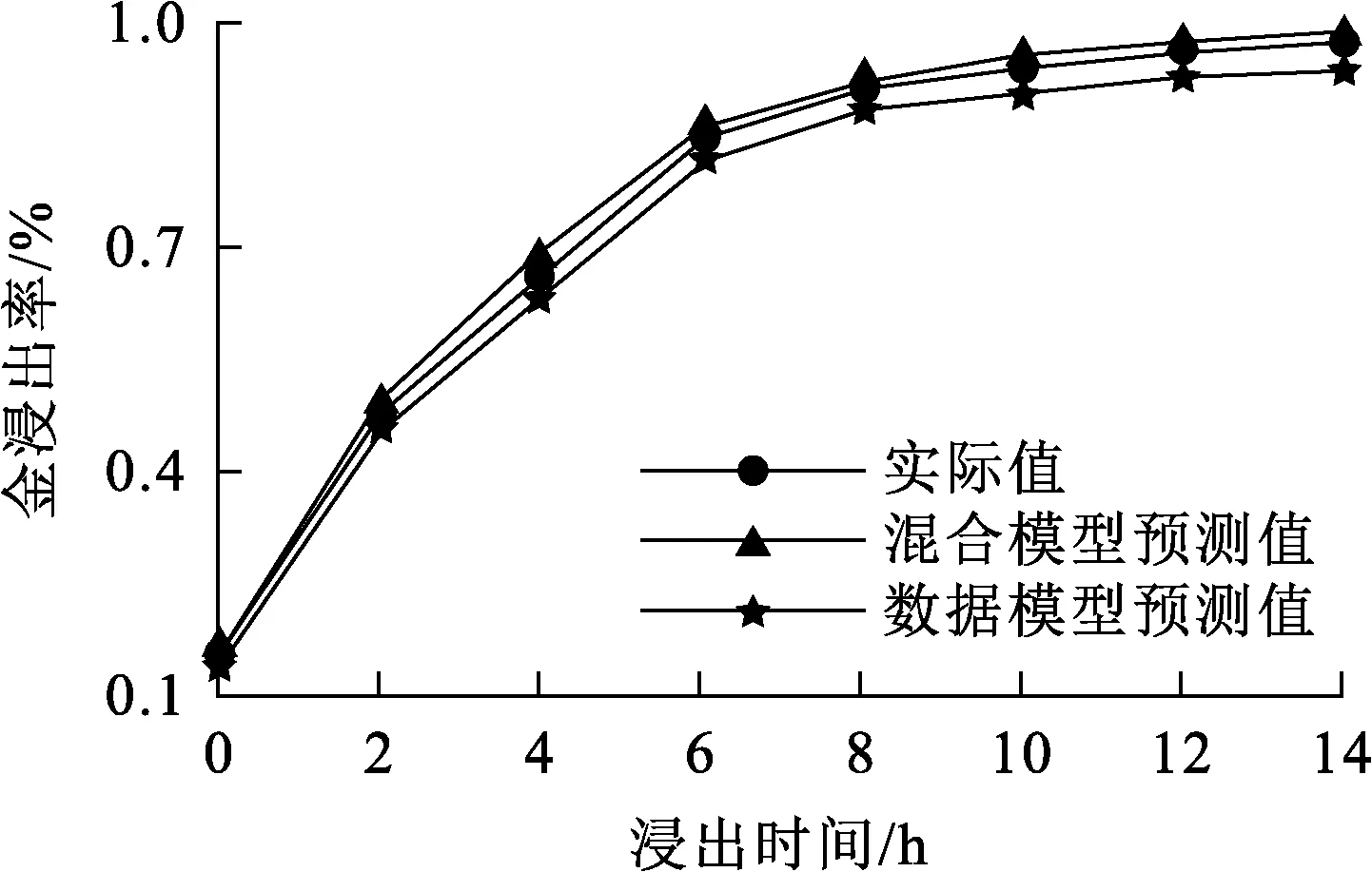
图6 金浸出率动态变化的预测结果
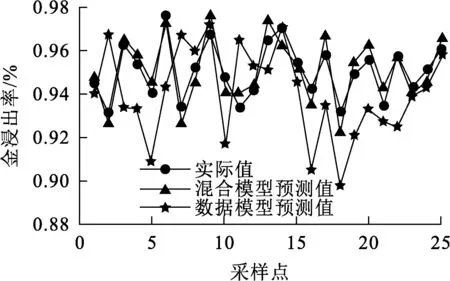
图7 稳态金浸出率的预测结果
串联混合模型和RBFNN数据模型的误差对比结果见表3。可以看出:基于串联混合模型的MAE和RMSE都小于RBFNN数据模型的对应数据。说明串联混合模型预测值精度和泛化能力更高,在实际工业中应用效果会更好。
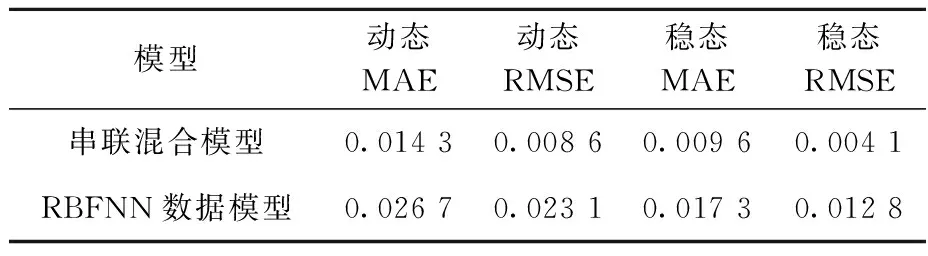
表3 串联混合模型和RBFNN数据模型的误差对比结果
3 串联混合模型的更新及仿真分析
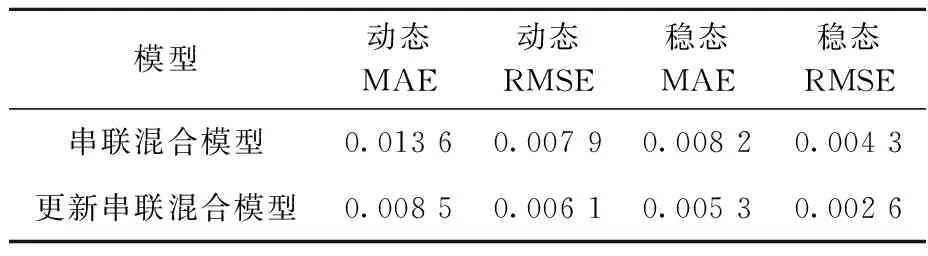
由于浸出过程具有时变性,模型精度会随时间延长而下降,若要精准预测,所建立模型需要具有更新能力。因此,需要通过对比预测值yp(t)和实际值y(t)之间误差判断是否需要进行模型更新。具体操作步骤为:1)初始化相关参数并设定标准误差值E=0.01;2)结合初始数据通过串联混合模型得到金浸出率预测值,将输入输出数据添加到历史数据中;3)再次计算得到金浸出率预测值;4)计算误差e(t)=|y(t)-yp(t)|,若e(t) 选取200组数据作为样本集,仿真分析浸出过程金浸出率的动态变化过程;选取25组数据进行测试,验证混合模型更新策略的有效性。预测结果如图8、9所示。串联混合模型和改进混合模型误差对比结果见表4。由图8、9和表4看出:模型更新后的预测值更接近实际值,说明对串联混合模型进行更新,可提高模型的准确性。 图8 金浸出率动态变化的预测结果 图9 稳态金浸出率的预测结果 表4 串联混合模型和更新串联混合模型的误差对比 针对金氰化浸出过程建立了一种具有高预测精度的串联型混合模型,并通过计算实际值与预测值之间的误差对模型进行更新,提高了模型的准确性。但由于实际生产过程具有一定的复杂性,所建立串联混合模型在实际应用过程中仍有一定的局限性,还有待进一步研究改进。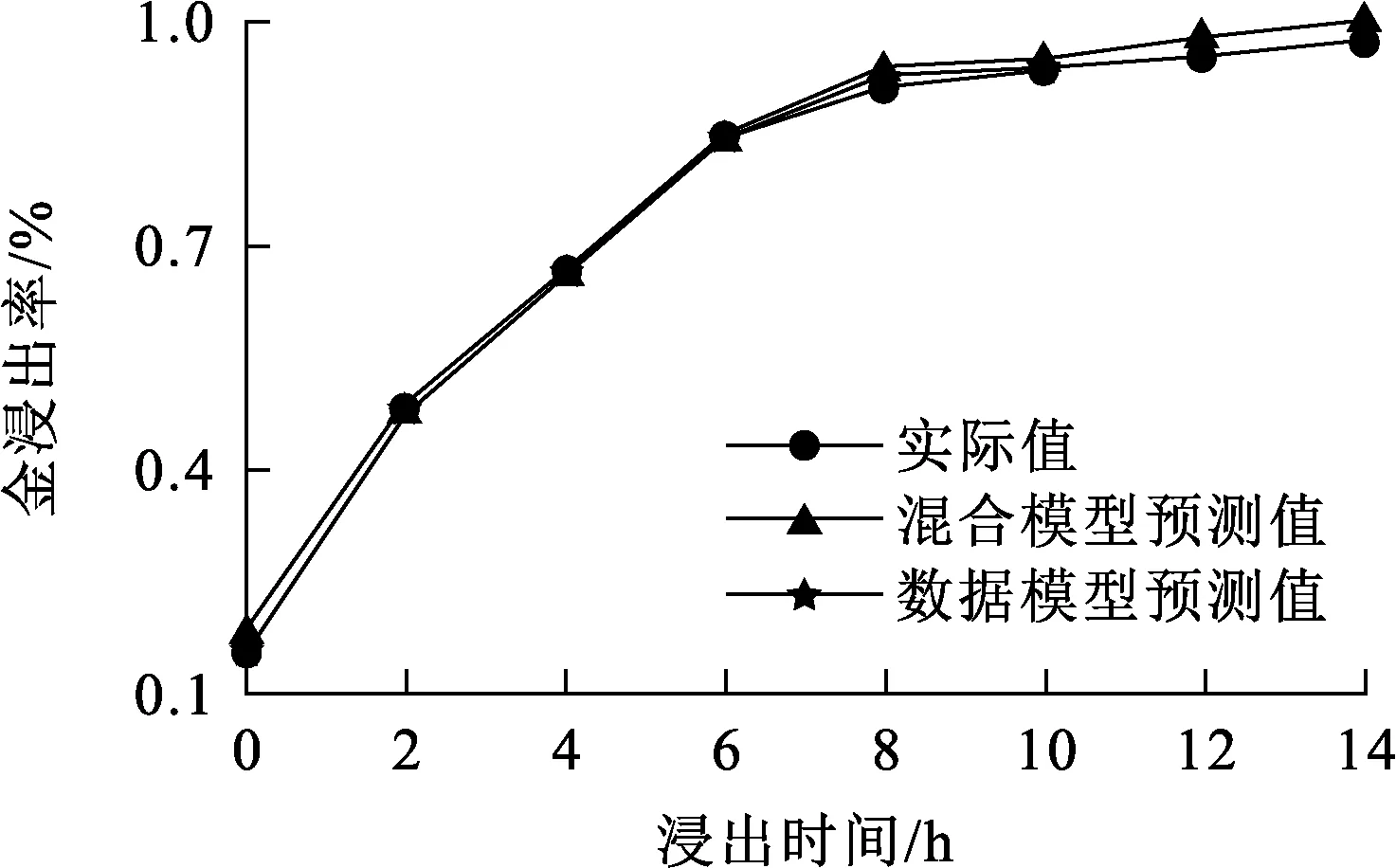
4 结论
