强度折减法在边坡锚喷支护中的优化设计

2023-08-05王鹏熊志鹏丁跃强徐文鹏张子键马鞍山学院建筑工程学院安徽马鞍山243000

安徽建筑 2023年7期

王鹏，熊志鹏，丁跃强，徐文鹏，张子键（马鞍山学院建筑工程学院，安徽马鞍山 243000）

0 引言

近年来公路、铁路等工程形成了大量路堑边坡，由于地质等因素引起的滑坡等现象导致了严重损失，边坡稳定已成为影响边坡施工进度、安全的重大问题之一[1-2]。国内学者对边坡稳定性分析包括极限平衡法、强度折减法等，取得了丰富的研究成果[3-4]。对边坡的加固方式有挡土墙、锚杆等，采用锚杆支护是边坡工程中常用的加固方式[5-6]。闫云明等[7]基于ANSYS 软件研究强度折减法在边坡中的应用。唐湖北等[8]基于GEO-SLOPE 软件，利用极限平衡法研究锚固角、锚杆长度及布设形式对安全系数的影响，总结出在边坡中下部埋设锚杆安全系数最大。陈国庆等[9]研究得出利用动态和整体强度折减法更利于边坡稳定性的判断及支护措施建议，动态强度折减法更适合于非均质边坡稳定性评价。张期树等[10]对锚杆布设优化设计，研究长中短型、中长短型、短长中型组合形式对安全系数的影响，并得出存在“组合-群锚效应”，优选出最合理的布置形式。本文以某地铁车辆段路堑边坡工程为研究背景，通过FLAC3D 软件建立模型并利用强度折减法进行数值模拟，研究锚杆长度、竖向和水平间距、水平面倾角及锚杆位置对安全系数的影响，优选出最合理的锚杆布置方式。

1 工程实例

狮山车辆段位于佛山市地铁3 号线北部，狮山工业大道东侧、博爱东路北侧地块，南跨科韵北路、科宝北路。选址地块现状为工业厂房，远期停车能力282辆/47 列，占地面积约33.9 hm2，地面标高18.6～27.5 m，场坪设计标高为19.7m，包含综合楼、运用库、检修库等建筑物，检修库南侧边坡为重力式挡土墙支护，采用放坡开挖。坡脚距检修库为19.5 m，边坡工程安全等级为一级。

边坡坡顶至坡底主要为填土＜1-1＞，高度约为6m。由坡底向下依次为粉质黏土＜5N-2＞，厚度约5 m；全风化碎屑岩＜6＞，厚度约3 m；强风化泥质粉砂岩、粉砂岩＜7-2＞，厚度约24 m。

边坡支挡结构为重力式挡土墙，施作重力式挡土墙前先进行土方开挖，放坡开挖后采取锚喷临时支护边坡，锚喷后即施作重力式挡土墙，待强度满足要求后即在挡墙与坡面间回填符合要求的材料并压实，边坡土方开挖实际坡率为1:0.5～1:0.75。

2 数值模型及数值模拟

2.1 边坡三维数值模型

边坡垂直高度为6m，坡率为1:0.5，根据岩土层厚度，通过FLAC3D 软件建立三维数值模型如图1 所示，坡顶至模型右边界15 m，坡脚至模型左边界7 m，地基宽度为25 m，沿纵向长度为6 m。固定约束地基底面、地基和边坡侧面，坡顶面不约束，共划分19152个网格单元、22273 个节点。采用莫尔库伦弹塑性模型，锚杆选择cable 单元，锚杆位置是通过两个节点坐标定义，即从begin位置到end 位置连成直线，锚杆构件是弹塑性材料，两点之间具有相同的横截面及材料参数的直线段[6]。

图1 边坡三维数值模型

2.2 物理力学参数

根据岩土工程勘察成果，查询岩土参数值表得出边坡和地基的物理力学参数，如表1。

表1 物理力学参数

2.3 数值模拟结果

数值模拟云图如图2 所示，该边坡安全系数为0.86＜1，不满足规范和设计要求。坡面位移较大，塑性区贯通至坡顶，出现圆弧滑动面，边坡不安全、稳定性较差，需采取措施防止潜在滑坡体在土体自重应力和外荷载作用下出现滑坡危险。

图2 数值模拟云图

3 锚杆支护优化设计分析

3.1 锚杆竖向间距对安全系数影响

在边坡埋设锚杆可以提高边坡土体抗剪强度，阻止滑坡体位移，使锚固结构与土体形成复合体，提高边坡土体的稳定性。该工程边坡临时采用锚杆支护，待重力式挡土墙施作完成且强度满足要求后回填土方，通过数值模拟对锚杆布置进行优化设计，既保证边坡临时稳定，又使成本最合理。锚杆物理力学参数如表2所示。

表2 锚杆物理力学参数

为了研究锚杆竖向间距对边坡影响，选取多组方案综合分析，锚杆竖向间距分别为0.5 m、1 m、1.2 m、1.5 m、2 m、3 m，即锚杆等间距设置11 排、5 排、4 排、3 排、2 排、1 排，边坡和地基土体的物理力学参数均保持不变。锚杆长度为4m，倾角为20 °，竖向间距分别为2 m、1.5 m、1 m 时数值模拟云图，如图3 所示。通过origin 拟合出安全系数与锚杆竖向间距的关系曲线如图4所示。

图3 锚杆竖向间距影响

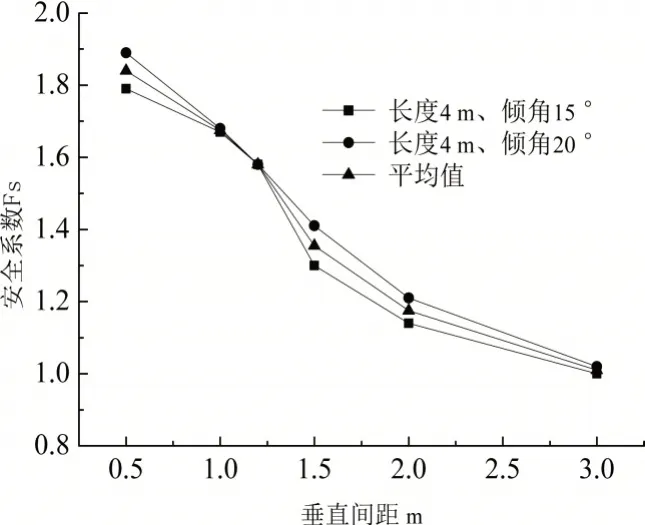
图4 安全系数与锚杆垂直间距关系

由图3、图4 分析可知，安全系数随锚杆竖向间距减小而增大，潜在滑坡体面积逐渐减小，锚杆穿过滑坡体深入土体。锚杆倾角20°，布置11 排、5 排、4排、3 排安全系数分别为1.89、1.68、1.58、1.41。布置11 排锚杆边坡稳定性更好，但成本更高。布置3 排锚杆安全系数略大于1.35，由于模拟并未完全考虑实际因素对边坡的影响，如连续降雨影响，因此不考虑此种布置。通过比选选择布置4排或5排锚杆，即竖向间距为1～1.2 m，安全系数随锚杆竖向间距的增加近似呈三次函数关系下降。

对数据平均值拟合得出安全系数与锚杆竖向间距之间的三次函数关系式如式（1）所示。

式中：Fs为安全系数；H为锚杆竖向间距，单位是m；回归系数R2=99.34%。

3.2 锚杆水平间距对安全系数影响

选择在坡面等分位置布置5 排锚杆，锚杆长度为4m，倾角为15°和20°，水平间距分别为0.5m、1m、1.5m、2m、2.5m、3m、4m、5m、6m，其余参数均保持不变。倾角20°，水平间距为1m、3m、6m 时，模拟云图如图5 所示。通过origin 拟合出安全系数与锚杆水平间距的关系曲线如图6 所示。

图5 杆水平间距影响Q

图6 全系数与锚杆水平间距关系

由图5、图6 分析可知，当锚杆长度为4 m、倾角为15 °和20 °时，边坡安全系数随锚杆水平间距的增加近似呈抛物线下降，下降速度逐渐减小；当锚杆水平间距小于2.5 m 时，边坡安全系数大于1.35。该工程地处南方，夏秋季节降雨较多，为防止雨水冲刷带来的潜在危害，应提高边坡的安全系数，为了保证边坡的稳定安全，同时又使支护成本降低，因此锚杆水平间距选取1～1.5 m 比较合适。

根据锚杆受力值可知，在边坡中下部的锚杆受力较大，靠近坡顶处的锚杆受力最小，且单根锚杆的中间部位受力最大，向两端逐渐减小；中下部锚杆的位移最大，靠近坡顶的锚杆位移最小。

对数据平均值拟合得出安全系数与锚杆水平间距之间的关系式如式（2）所示。

式中：Fs 为安全系数；L 为锚杆水平间距，单位是m；回归系数R2=99.59%。

3.3 锚杆长度和倾角对安全系数影响

坡面等分布置5排锚杆，水平间距为1 m，长度分别为3 m、4 m、5 m、6 m、7 m、8 m，锚杆与水平面夹角分别为0 °、5°、10°、15°、20°、25°、30°、35°、40°、45°、50°、60°，进行72次模拟。安全系数与锚杆长度及倾角关系如图7所示。

图7 安全系数与锚杆长度及倾角关系

由图7 分析可知，当锚杆长度保持不变时，边坡安全系数随锚杆倾角的增加先增加后近似抛物线减小，不同长度的锚杆最优锚固角度也不同，最优锚固角度随锚杆长度的增加逐渐减小，最优锚固角度范围为5～25°。

当锚杆倾角小于25 °时，安全系数随锚杆长度增加先增加后减小，存在最优锚固长度，不同倾角的最优锚固长度也不同；当倾角大于25 °时，随锚杆长度增加逐渐减小，最终趋于稳定；当倾角为10～20 °时，安全系数相对较高，边坡稳定性较好。

为了保证边坡的稳定、安全，可选择锚杆长度为4 m、倾角为15～20 °的布置方式。

3.4 锚杆位置对安全系数影响

为研究单排锚杆位置对边坡安全系数的影响，分别在边坡11个等分位置设立单排锚杆，第一次只在边坡布置第1排锚杆，第二次只布置第2排锚杆，以此类推，研究边坡单排锚杆位置对边坡安全系数的影响。通过origin拟合出单排锚杆安全系数与锚杆位置关系如图8所示。

图8 安全系数与锚杆位置关系

由图8 分析可知，当锚杆长度保持不变且单排锚杆位置由坡顶向坡脚移动时，边坡安全系数先增加后减小，近似呈马鞍形曲线变化。单排锚杆布置在第8排（距坡底垂直距离2 m）位置时安全系数最大，对提高边坡稳定性和安全性效果最好。

边坡中下部的安全系数较高，这与图7 中锚杆受力规律基本一致，即中下部锚杆受力较大，在边坡上部和坡底处锚杆受力较小，因此在边坡中下部布置锚杆有利于提升边坡稳定性和安全性。

综上所述，对比分析并优选出最合理的锚杆布置方式，可在坡面布置4 排（边坡土质均匀且良好）或5 排锚杆（边坡有杂填土等非均质），长度为4 m，倾角为15～20 °，水平间距为1～1.5 m。既保证了边坡的稳定安全，又控制了施工成本。现场实际施工过程中，在坡面不同位置布置了监测点，实测数据表明重力式挡土墙施工及夯实墙后填土期间边坡位移较小，未出现滑坡等险情。重力式挡土墙、锚杆支护、墙后填土共同保证了该边坡的长久稳定。