基于皮尔逊相关系数与SVM的居民窃电识别

郭亮,郭子雪,贾洪涛,范若禹

(1.国网保定供电公司,河北 保定 071000;2.河北大学 管理学院,河北 保定 071002;3.保定浪拜迪电气股份有限公司,河北 保定 071051;4.布朗大学 经济系,罗德岛州 普罗维登 00785)

随着电价市场化改革,国内电力市场不断完善,市场经济平稳运行,但不免存在不法窃电行为,居民窃电只是其中1种.窃电行为不仅扰乱了正常的电力市场秩序[1],破坏了市场竞争的公平性,对电力企业造成了严重的经济损失[2-4],同时也破坏了电网运行的安全性、可靠性,对人民的安全用电构成了威胁,所以有效打击窃电等违法行为成为了电力企业日常工作之一.基层班组常采用地毯式搜查的工作方式不仅工作量大,排查难度高,而且现场排查的精确度较低,因而急需一种高效的窃电用户检测手段.随着近些年来用电采集系统的不断完善和发展,电力用户的用电量、采样电压、采样电流等用电信息不断呈现在用电检查人员面前,如何利用这些用电信息精确发现窃电用户,排查窃电现象,是目前反窃电研究领域的一大热点和难点.

国内外许多学者已对基于电力大数据的窃电用户检测方法进行了大量研究.文献[5]通过标准化后的协方差衡量非技术线损与用户日用电量之间的相关性,实现了对固定比例窃电用户的检测.文献[6]利用边缘计算对低压用户窃电进行检测.文献[7]利用电力用户的电力数据,通过欠压法、欠流法和扩差法进行数据分析,对低压单相用户进行窃电检测和辨识.文献[8]通过对窃电用户的用电数据进行相似性度量,得出窃电相似度矩阵,利用该矩阵通过聚类的方法检索出电力数据库中的相似用户,结合人工经验判断出该户是否为窃电用户.文献[9-10]通过密度聚类的方法,挖掘分析用户窃电的可能性.文献[11]提出了一种基于改进K-means算法和用电大数据的新型窃电识别模型.文献[12]通过K-means聚类和SMOTE算法生成窃电样本,提出了一种基于差分进化SVM的识别方法,提高了窃电行为的识别率.文献[13]通过将电量波动特征和一类支持向量机相结合,提高了窃电辨识模型的准确率和效率.文献[14-15]通过大数据分析和相关性计算,对用户是否存在窃电现象进行识别.文献[16]提出了2步窃电检查策略,利用基于卷积自编码器的改进回归算法,提高了窃电行为识别的准确率.

针对窃电用户数据搜集困难、逐户搜索窃电用户工作量大的问题,本文提出了一种皮尔逊相关系数和SMOTE算法相结合生成窃电样本数据库,再通过支持向量机训练样本数据生成居民窃电识别数学模型的方法.该方法首先通过计算窃电用户日用电量和所在台区日线损量之间的皮尔逊相关系数,判断并收集窃电用户的有效窃电数据,如用户日电压波动率、用户零火电流差值平均值或最大值等,形成窃电用户的有效窃电特征数据库;其次针对窃电用户数量相对较少、窃电数据收集较为困难的问题,利用SMOTE算法对有效窃电特征数据库进行扩展丰富;然后根据数据库利用支持向量机对有效窃电数据进行训练,从而生成居民窃电识别的数学模型;最后通过该数学模型对用户用电数据进行分类,筛选出可疑窃电用户,再经现场核实可知,本文提出的方法具有有效性和可行性,为电力企业提供了一种高效精确的反窃查违方法.

1 研究思路

本文通过用电采集系统对用户的用电信息进行收集,以用户的日用电量、所在台区当日线损率、每日零火电流和每日电压波动率表示用户的用电特征,通过分析对比用户用电特征对用户是否窃电作出判断.首先需要建立窃电用户和正常用户的用电特征数据库,在实际工作中正常用户数量远远大于窃电用户,因此如何有效收集窃电用户的窃电特征数据成为了模型建立的基础,根据班组工作记录中的窃电用户信息,采用皮尔逊相关系数法计算窃电用户日用电量和所在台区当日线损率之间的皮尔逊相关系数,利用相关系数的大小来判断窃电用户在该时间段内是否有窃电行为,再利用SMOTE算法丰富有效窃电数据库;在建立窃电用户和正常用户用电特征数据库的基础上,利用支持向量机对窃电识别数学模型进行训练,根据训练完成的数学模型对电力用户进行识别检测,再通过现场情况核实判断窃电检测模型的有效性和准确性.

2 研究方法与窃电识别数学模型

2.1 皮尔逊相关系数和SMOTE算法

皮尔逊相关系数常用于计算2变量之间的相关性,本文通过计算窃电用户日用电量和该户所在台区当日线损电量间的皮尔逊相关系数,来判断该户该时间段是否窃电.当2组变量分别为X=(x1,x2,…,xn),

Y=(y1,y2,…,yn)时,变量X和Y的皮尔逊相关系数r计算公式如下：

其中,r代表皮尔逊相关系数,X、Y代表变量,μX为变量X的平均值,μY为变量Y的平均值,r绝对值越大,用户窃电可能性越高,r的具体含义如表1所示.

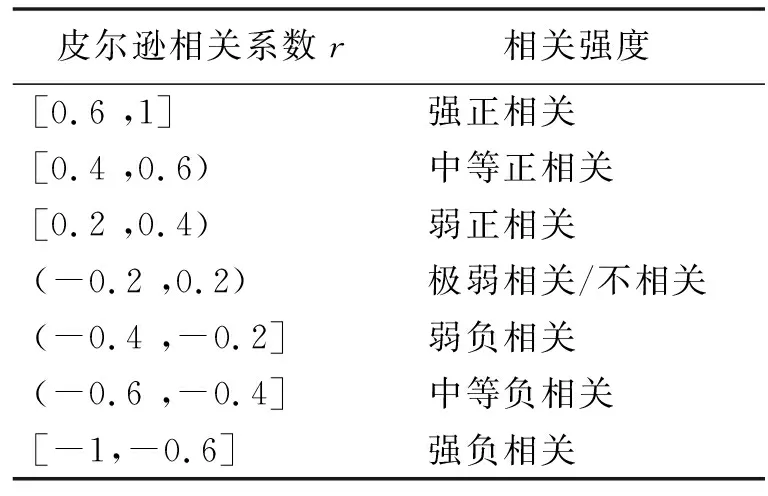
表1 皮尔逊相关系数r具体含义

SMOTE(synthetic minority oversampling technique)算法是一种基于人为合成样本数据的过采样方法,该方法是对随机采样方法的一种改进.随机采样方法通过对少数类样本数据进行随机插值处理生成新的样本数据,而SMOTE算法首先利用欧氏距离计算样本点之间的距离,再利用K邻近原则筛选出每个少数类样本点的K个相邻样本,最后通过随机选取的相邻样本和少数类样本点进行插值计算从而生成新样本数据点.该方法在有效降低样本空间不平衡度的同时,也避免了少数样本重复率过高而引发过拟合的现象.假设少数样本空间为{x1,x2,…,xn},通过算法生成的少数类样本为yj=xi+rand(0,1)*(xi-xm),其中,xm从样本xi的K邻近样本中随机选取.

2.2 基于支持向量机的窃电识别模型

2.2.1 窃电识别模型的建立

支持向量机(support vector machine, SVM)是典型的二分类算法之一,其数学模型是在数据特征空间上寻求最优分类超平面使得支持向量与分类超平面间的间隔最大化.在线性可分的样本空间上,支持向量法寻求的最优分类平面为一线性直线;在线性不可分的样本空间上,常通过核函数将线性不可分的样本空间映射到高维样本空间,使高维空间中的样本线性可分.在反窃电应用中,居民用户和所属台区的数据样本线性不可分,其模型求解过程与核函数的选取息息相关.窃电识别模型的支持向量机原理如图1所示.

图1 支持向量机的一维数学模型Fig.1 1D mathematical model of SVM

假设图1中用户用电数据线性可分,圆形代表窃电用户用电数据,三角形代表正常用户用电数据,直线L0为用电数据空间中的一个分类平面,标红数据样本为两类用户用电数据中距离直线L0最近的点,称为窃电识别模型的支持向量,支持向量距离分类面L0的距离相等.空间中能够将三角形和圆形两类数据分开的平面无数,窃电识别的支持向量机模型寻找到其中一个平面,使得支持向量距离分类面的间隔最大,该分类面称为最优分类面,如何求解最优分类面成为了问题的关键.

假设存在一个n维平面ωTx+b=0 ,可将N个用户的用电数据xi=(xi1,xi2,…,xin)分为2类,分类标签计为yi,当yi=1时,ωTx+b≥0;当yi=-1时,ωTx+b<0,其中ωT=(ω1,ω2,…,ωn).点xi到平面的距离为

d=(|ωTxi+b|)/(‖ω‖).

在寻找最优平面时,首先需找到N个用电数据点中距离该平面的最近的数据点

该数据点为当前平面的支持向量.又因为不同平面对应着不同的支持向量,为了保证最大的区分度,最优平面应使支持向量到该平面的距离最大,所以此时最优平面选取的数学模型为

因为yi(ωTxi+b)>0,所以对最优平面的数学模型化简如下：

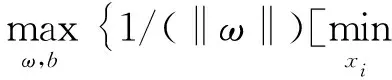
综上所述基于SVM的窃电识别模型如下所示：

2.2.2 窃电识别模型的求解

文中xi为四维向量,xi=(xi1,xi2,xi3,xi4)T,xi1为用户日用电量,xi2为用户所在台区当日线损,xi3为用户当日零火电流差值的最大值,xi4为用户当日用电电压波动值;yi为用户标签,当yi=-1时,该用户为窃电用户,当yi=1时,该用户为正常用户;ω和b分别代表窃电识别模型分类平面的参数,其中ω=(ω1,ω2,ω3,ω4)T,为窃电识别模型的待求参数.

利用拉格朗日乘子法构建拉格朗日函数如下所示：

通过拉格朗日函数可将窃电识别问题从带约束的优化问题转换为无约束的优化问题：

其中,αi为窃电识别模型的拉格朗日因数.

通过对偶转换可得原问题的对偶问题为

利用卡罗需-库恩-塔克(KKT)条件可得

因此当αi≠0时,存在(xk,yk),使得1-yk(ωTxk+b)=0.

将KKT条件代入对偶问题化简,可得

通过计算出αi可以对ω和b进行求解,最终可获得最优分类面.由于窃电用户数据线性不可分,可以通过核函数将窃电用户的低维数据映射到高维,使得窃电用户数据线性可分,再对SVM数学模型进行求解.综上所述在实际应用中窃电识别的支持向量机模型为

其中,特征转换函数φ(x)将低维数据x映射至高维数据空间.

为了简化运算引入核函数K(xi,xj)=φ(xi)Tφ(xj),常用的核函数有如下2种：

2)高斯核函数：K(xi,xj)=e-(xi-xj)2/(2σ2 ).

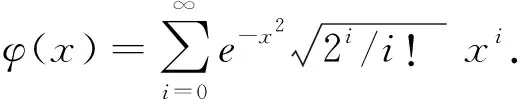
由此可见,高斯核函数可将特征向量x投影到无限维空间去,理论上可将任意线性不可分数据集转换成线性可分数据集,因此本文选取高斯核函数对窃电识别模型进行求解.

3 数据验证

3.1 数据来源

利用反窃电工作中所收集的窃电用户信息,再通过用电采集系统对窃电用户的用电信息进行收集,收集的历史用电信息主要包含用户当日用电量、用户所在台区当日线损量、用户当日零火电流差值最大值以及用户当日用电电压波动情况等.

3.2 数据处理与分析

利用MATLAB对数据进行分析处理,将窃电用户A和正常用户B的用电量与所在台区当日线损量的关系图绘制如图2所示.

a.窃电用户;b.正常用户图2 用户日用电量与所在台区当日线损量关系Fig.2 Relationship between daily power consumption and daily line loss

观察图2不难发现,窃电用户的日用电量与所在台区当日线损量基本呈正相关态势,窃电用户用电量越大时,台区线损量也越大,即窃电用户用的越多窃电越多,台区损失也越大,而正常用户的日用电量和所在台区当日线损量无明显相关关系.通过皮尔逊相关系数计算可得,窃电用户的相关系数为0.206 1,正常用户的相关系数为0.026,根据表1可知,窃电用户的日用电量和所在台区当日线损呈弱正相关,正常用户的日用电量与所在台区当日线损不相关,由此可见窃电用户的日用电量与所在台区当日线损呈一定的相关性.

由于窃电用户较少,窃电用户的用电特征数据搜集较为困难,所以采用SMOTE算法,对筛选的窃电用户用电特征数据进行插值运算,将55个窃电用户原始用电特征数据扩展为3 760个特征数据点,同时收集了2 000个正常用户的用电特征数据,正常用户的特征数据标签计为+1,窃电用户的特征数据标签计为-1,将正常用户与窃电用户的用电特征数据相结合构成用电特征数据库,通过MATLAB中的libsvm数据分析工具,对收集的用电特征数据进行求解运算,可以得到疑似窃电用户的判别模型,本文采用RBF核函数,调节模型参数σ,可使模型判别准确率不断变化,利用验证数据库可得σ与SVM模型的研判准确率关系如表2所示.

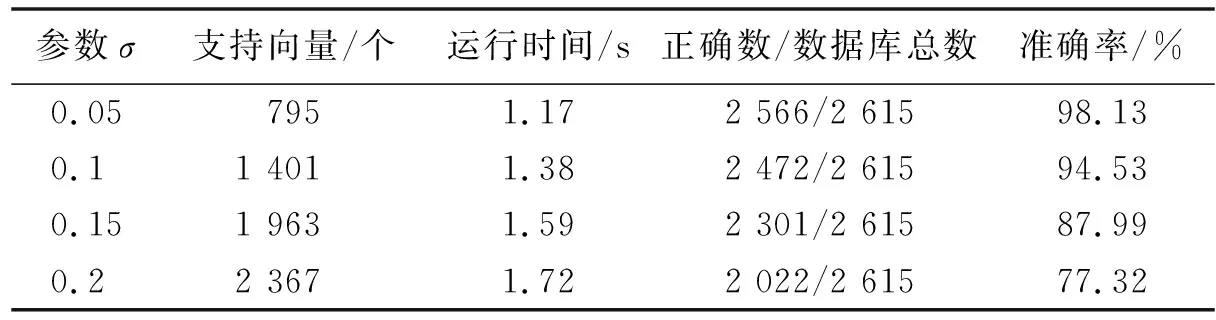
表2 参数σ与模型准确率关系

由表2可知参数σ取值较小时,选取支持向量个数少,程序运行时间短,模型研判准确率高,因此在本文的研究中采取σ=0.05的SVM数学模型.

在使用训练成功的数学模型进行分类时,若用户连续3 d的判断结果为窃电用户则其窃电概率较高,需结合现场核实,对用户进行排查处理.本文通过训练好的数学模型,对班组服务区内的N台区进行分析,发现户号为065****778的用户模型预测结果连续3 d判断标签为窃电用户,再通过用电采集系统收集该户与正常用户连续1周的零火电流数据,用电采集系统可对用户进行96点采集,即每15 min对用户数据进行一次采样,本文通过降采样的方法,提取用户整时刻点的用电数据,将波形绘制如图3所示.

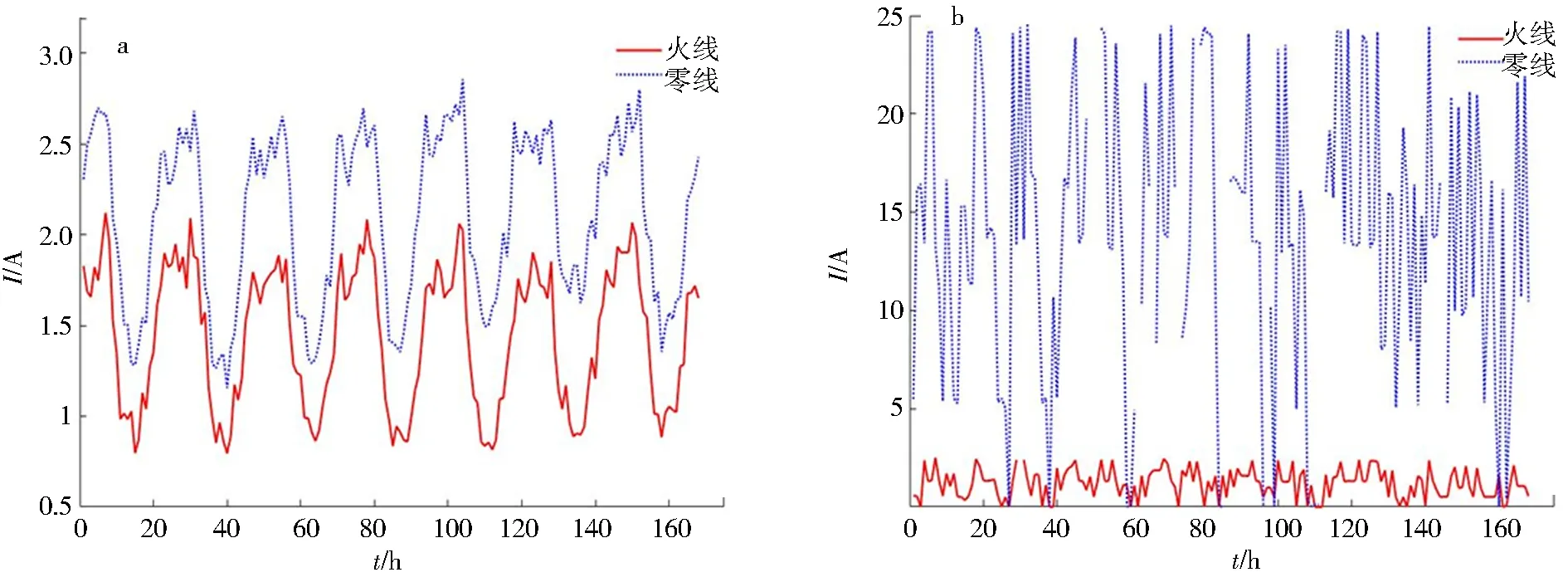
a.正常用户;b.异常用户图3 用户电流波形对比Fig.3 Electricity wave comparison between abnormal user and normal user

图3可知,异常用户零火电流波形相差较大,火线电流数值几乎为零,零线电流数值较大且2波形间的相似度较低.与此相反,正常用户的零火线电流数值相差不大,且波形具有明显的相似性.由此根据数据特征初步判断,该异常用户为火线短接的窃电用户.

前往用户用电现场进行核实,现场检查结果如图4所示.

图4 异常用户现场Fig.4 Reality situation of abnormal user

经用电检查发现,该用户私自打开电表,在火线进出线接线柱上绑绕铜丝,以达到电表少计量甚至不计量的目的,该行为属窃电行为,该用户亦对窃电行为供认不讳,依据供电营业规则,用电检查班组已对该电表进行处理,并追补电费和罚款.

4 结论

本文针对窃电用户用电数据搜集困难、用电检查班组查窃电任务量大的实际问题,提出了一种低压居民窃电检测的判别模型.该模型通过皮尔逊相关系数收集窃电用户的有效窃电数据,利用SMOTE算法对有效窃电数据进行平衡生成用电特征数据库,再结合支持向量机的方法对数据库进行模型解算.该模型可以高效地锁定服务区内的疑似窃电用户,工作人员再结合用电采集系统进行分析,可以精准地锁定窃电用户,对窃电等违法行为实施精确打击,大大减少了用电检查人员的反窃电工作量,提高了基层班组的工作效率,同时为用电检查班组在低压用户的反窃电工作提供了思路.