面向入侵检测的元图神经网络构建与分析

王振东 徐振宇 李大海 王俊岭

网络技术高速发展的同时,计算机病毒、网络入侵纷至沓来,给网络安全带来极大挑战[1].对此,国内外相关学者对入侵检测技术进行了深入研究,提出了机器学习、数理统计、神经网络等[2-5]多种检测算法.然而,传统机器学习方法普遍强调对特征的选择和参数训练,且运行时间成本较高;而数据挖掘算法对噪声较为敏感,面对噪声数据较多的数据集时易出现过拟合现象[6];深度学习方法擅长从海量、高维数据中提取特征信息,降低噪声对算法性能的影响,深度学习技术已在图像识别、图像分割、文本分析等领域得到了广泛的应用[7-9].通过设计合理的网络结构,深度神经网络可有效控制神经网络的参数量,确保网络性能的同时,降低神经网络的运行成本[10].

目前,多位学者使用深度神经网络,如卷积神经网络(Convolutional neural network,CNN)、长短期记忆网络(Long short-term memory,LSTM)、循环神经网络(Recurrent neural network,RNN)设计了一系列入侵检测算法.CNN 方法将一维入侵数据转换为二维 “图像数据”,再利用CNN 对入侵数据进行处理.该方法考虑了卷积神经网络中卷积核内各特征间的相互作用[11],特征数据不再孤立.如文献[12]借鉴了Google 团队提出的Inception结构,设计了一种具有多种不同尺寸卷积核的卷积神经网络;文献[13]基于LeNet-5 设计了一种具有不同尺寸卷积核的深度卷积神经网络.上述两种基于CNN 的入侵检测算法均可通过不同尺寸卷积核提取特征间的相互关系,但存在如下缺点: 1) CNN仅能处理欧氏空间数据,难以挖掘任意两个特征数据间的复杂图结构关系;2)大多数经典CNN 模型(如VGG[14]、GoogLeNet[15]、ResNet[16]等)结构复杂、参数量大、运行时间成本高,将经典CNN 模型引入入侵检测领域需要着重考虑运行成本.RNN 与基于RNN 改进的LSTM 神经网络算法将各样本特征数据视为序列数据,并按照序列顺序输入LSTM与RNN.LSTM 与RNN 方法同样能够挖掘特征数据间的依赖关系,文献[17-19]均利用LSTM/RNN挖掘出网络入侵数据特征值之间的相互关系,均在入侵检测领域取得不错效果,由于按照入侵检测数据集中特征数据排列顺序进行输入,因此难以准确建立样本特征数据间的联系,且此类算法同样只能处理欧氏空间数据,同样难以挖掘任意两个特征数据间的复杂图结构关系.

事实上,入侵检测数据集的各条样本均存在多个特征数据,而不同特征数据间可能存在强弱关联,该关联无法在欧氏空间进行精准的数学描述.以NSL_KDD 数据集为例,该数据集样本中存在连接持续时间、协议类型、目标主机的网络服务类型、连接正常或错误的状态、数据的字节数、访问系统敏感文件和目录的次数、登录尝试失败的次数等41个特征数据.其中,连接持续时间与数据的字节数存在强关联关系,而协议类型与目标主机的网络服务类型存在弱关联关系.数据特征间的强弱关联构成非欧氏空间的图结构关系,对该图结构的深入挖掘并将挖掘结果用于辅助神经网络的分类决策,可有效提高神经网络的入侵检测性能.目前,处理非欧氏空间数据的深度学习典型方法为图神经网络(Graph neural network,GNN)[20-23],但GNN 只能处理样本间的已知图结构关系[20-23],而对样本内部特征的图结构关系未知的场景无能为力.

对此,本文设计了一种能够挖掘、处理样本数据间未知关联关系的新型神经网络 — 元图神经网络(Meta graph neural network,MGNN),并将其应用于网络入侵检测.MGNN 重新定义了网络内部的运算方式,在样本的特征数据间图结构关系未知的前提下,建立单条样本特征数据内部的图结构关系,并实现对该图结构关系的深入挖掘.在挖掘过程中,利用梯度下降算法对图结构进行优化,并根据祖孙节点间的图信息传播(Multi-generation graph information propagate between nodes,MPS)过程对图结构关系进行处理.针对MPS 过程可能出现的信息湮灭现象,提出一种反信息湮灭策略.为了更加精确地刻画特征数据间的强弱关联,设计了注意力损失函数,并通过影响图结构邻接矩阵实现对图结构关联关系的加强或削弱.

为了深入阐述MGNN 的运行原理,本文在第1 节介绍了MGNN 对特征数据未知图结构关系的处理方式,并解释了未知图结构关系如何影响样本初代特征数据;第2 节对基于MGNN 搭建的神经网络的消息前向传播过程和梯度信息反向传播过程进行了详细分析;第3 节指出了MGNN 对样本特征数据的图结构关系处理中存在的不足,并使用注意力函数机制与反信息湮灭策略进行改进;第4 节设计了多种基于MGNN 搭建的神经网络,并利用上述网络对UNSW_NB15、NSL_KDD、CICDoS 2019 三种入侵检测数据集进行实验测试,验证MGNN在入侵检测领域的优越性能.最后,对全文进行了总结,并对MGNN 的下一步研究进行了展望.

1 MGNN 的结构与运算

MGNN 的处理流程如图1 所示.图1 中,MGNL(Meta graph network layer)为元图网络层(详见第1.1 节和第1.2 节),NN (Neural network)为经典神经网络,例如深度神经网络(Deep neural network,DNN)、CNN、RNN、LSTM,本文采用DNN.图1 中MPS 过程在元图网络层MGNL 中完成,本文在第1.2.3 节中将有详细介绍.由图1 可知,样本数据进入MGNN 后样本的特征值首先被元图网络层(MGNL)随机组织为一个图结构(详见第1.1 节和第1.2 节),然后利用该图结构进行MPS 过程,获得聚合了子孙节点信息的特征数据,再将聚合了子孙节点信息后的特征数据传入下层神经网络进行更深层次的特征提取,通过多次MGNL 对特征数据内部图结构挖掘、整合,获得考虑了特征数据之间相互关联关系的特征值,最后利用这些特征值对网络入侵数据进行分类.

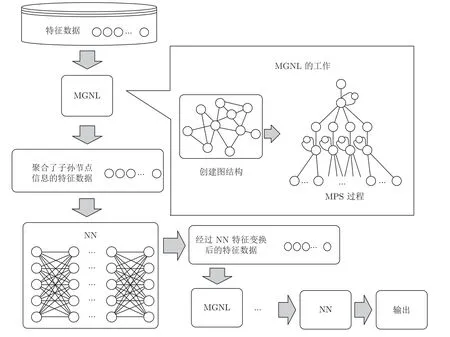
图1 MGNN 结构与处理流程Fig.1 Structure and processing flow of MGNN

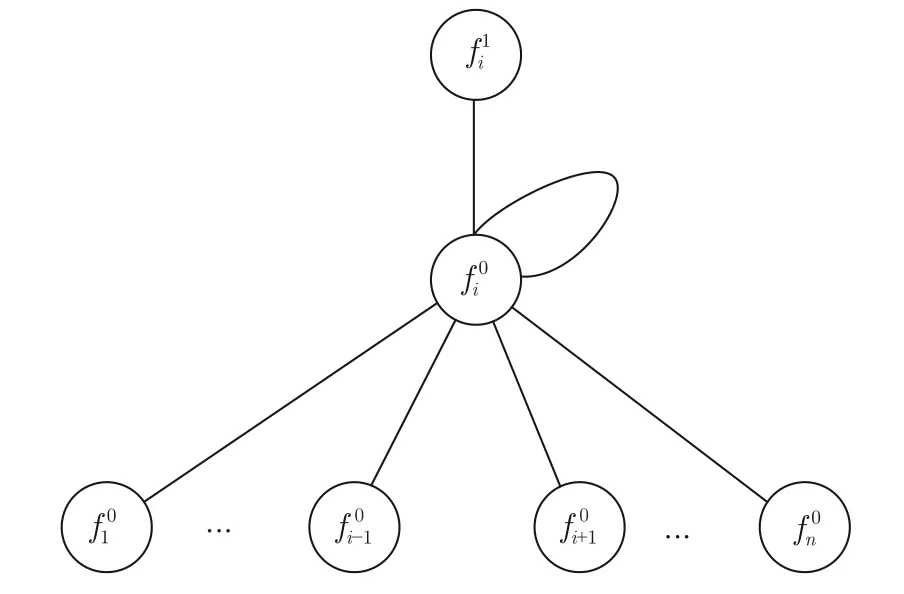
图2 MGNL 中单代父子结点间信息传递结构Fig.2 Information transfer process of parent-child node between single generation in MGNL

1.1 元图网络层MGNL

传统全连接神经网络的核心为线性层,其运行过程为

其中,X表示输入,W表示权值,B表示偏置,f(·)为激活函数.由式(1)可知在线性层中,神经网络将样本的特征数据视为相互独立,并单独为各个特征数据分配权值.

MGNN 的核心为元图网络层(MGNL),MGNL的功能在于对样本特征数据内部隐藏的图结构关系进行挖掘与处理,具体流程详见第1.2 节.MGNL相对于其他神经网络层而言,仅在于内部运算方式不同,核心仍为矩阵运算,因此MGNL 能够兼容其他各种网络,与其组成结构各异的复杂神经网络.为了更好地展现MGNN 的特点,说明MGNN 对原始神经网络性能提升的作用,减少其他网络层对特征数据内部关系的影响,本文采用MGNL 与全连接层组合构建MGNN.

1.2 MGNL 图信息传播

1.2.1 MGNL 初始化

网络入侵数据样本特征数据的图结构关系未知,为了能够考虑样本特征间的相互影响,需先获取一个能够反映样本特征间图结构关系的表达方式,在数据结构中通常使用邻接矩阵表示图结构关系.据此,首先定义一个随机初始化的矩阵Mg,并将Mg视为特征数据内部图结构的邻接矩阵,如式(2),其中,n为入侵数据样本中特征数据的个数,a1i为样本的1 号特征项与第i号特征项间的联系权值,其值越大表示两个特征项联系越紧密.同理,ani表示样本的第n号特征项与第i号特征项间的联系权值,Mg中其余元素的含义依此类推.

随后,定义一个大小与Mg相同的对称矩阵Mf,在Mf中对角线元素均为0,其余位置元素为1,如式(3)所示.

将Mg矩阵与Mf矩阵中对应位置的元素相乘,得到消息传递矩阵Mp.如式(4)所示,Mp中对角线元素为0,其余位置元素与Mg矩阵保持一致.

其中,⊙表示哈达玛积.

1.2.2 单代父子结点间的图信息传播

为了将入侵样本中的所有特征数据按照式(5)定义的规则进行更新,定义一种矩阵运算公式,即

其中,F0为数据样本的所有特征值的向量表示,F1为该样本的特征数据经过SPS 融合后的值.

1.2.3 多代祖孙结点间的图信息传播

同样,每次只考虑某个样本内的特征数据fi,根据图结构邻接矩阵Mg,对fi使用广度优先搜索遍历,建立以fi为根节点、深度为1 的搜索树.然后,对fi的所有子节点使用广度优先搜索遍历,建立以各子节点为根节点、深度为1 的搜索树.重复上述过程n次,将最终得到的所有搜索树组合成如图3所示的树结构,并以此作为MGNL 多代祖孙结点间的信息传递结构图.为了能够顺利进行多代节点间的消息传递,在MGNN 中指定最底层消息为某数据样本的原始特征值.图3 中样本的特征数据由底层向上融合,并影响根节点fi的值,此过程定义为样本特征数据祖孙结点间的图信息传播(MPS).

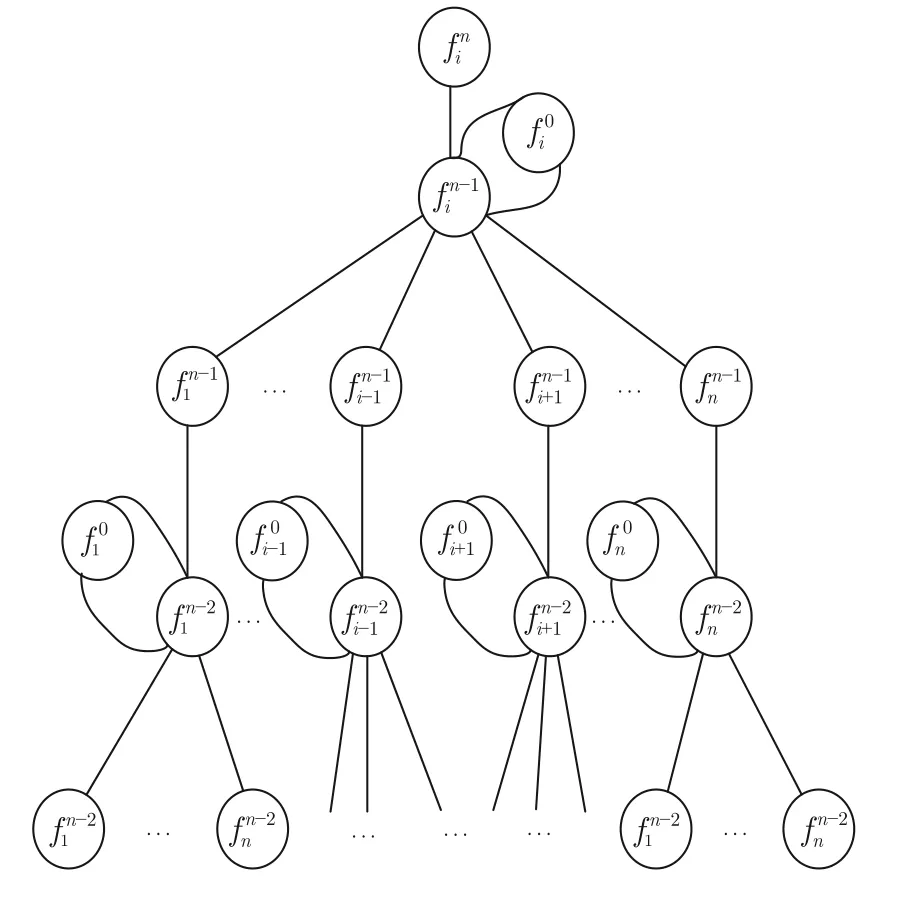
图3 MGNN 祖孙结点间信息传递结构Fig.3 Information transfer process between grandparents and grandchildren in MGNN

分析图3 可知,MGNN 中样本所有特征数据执行完MPS 过程的数学描述为

式中,F0为某数据样本的所有特征数据的向量表示,Fn-1为经过n-1 代MPS 过程后的样本数据,Fn为经过n代MPS 过程后的样本数据.Fn-1×表示将第n-1 层结点信息聚合至第n层结点,该部分并不包括第n层结点的初代信息,故在进行第n代MPS 过程时需加上其初代信息F0.

MGNN 中只有矩阵Mg参与网络训练过程,需要训练的参数量为N×N,其中,N为一个样本中特征数据的数量.在相同纬度映射条件下,相对于传统线性层而言MGNN 可以省略偏置项,可减少N个待训练的参数,并且能够实现数据样本内部特征数据中未知复杂图结构关系的挖掘、分析与处理.

2 MGNN 中信息的传播过程分析

2.1 单层MGNN 信息前向传播过程

在只有单层MGNL 的MGNN 中,为了完成分类任务,需要将数据按照分类目标进行维度转换,因此需在MGNL 后链接全连接层,全连接层之后接sigmoid 或softmax 函数,并将全连接层输出的数值转化为概率值,信息的前向传播过程描述为

其中,F0为输入至神经网络中的样本特征值,Fn-1为经历了n-1代MPS 过程后的样本特征值,Fn为经历了n代MPS 过程后的样本特征值,W为全连接层中的权值,B为全连接层中的偏置,神经网络输出值a与标签值y之间的损失值为L.

2.2 单层MGNN 信息反向传播过程

依据式(8)和式(9),利用链式求导法则可知,针对W的信息反向传播过程为

由式(8)可知,在MGNL 中信息的前向传播过程为递归嵌套过程.利用链式法则,对Mp进行梯度信息反向传播时需要同时考虑Fn-1与Mp.将式(8)展开得式(11)～ (13):

重复使用式(8),直到式(12)中所有的上标均变成0,得到

在式(13)和式(14)中,Fn表示经过n代MPS过程后的样本特征数据,(Mp)n和(Mp)n-1为矩阵Mp的n次方、n-1 次方.

2.3 多层MGNN 信息前向传播过程

现有研究表明,在一定范围内增加神经网络的层数可以提高神经网络的辨识能力.实际使用中,可以堆叠多层MGNL,从而获得表达能力更强的多层MGNN.由第1 节的分析可知,MGNL 并不具备数据维度变换能力,故在多层MGNL 条件下,需要在MGNL 中间添加一层或多层线性层,以实现数据维度的改变.因此,MGNL 与线性层穿插方式的不同可演化出丰富的网络结构,下面以MGNL 与线性层交替排列的网络结构为例,展示多层MGNN中信息的前向传播过程:

2.4 多层MGNN 信息反向传播过程

对式(15)～ (25)依据链式求导法则,得到整个神经网络中线性层的权值W进行反向传播过程.

为方便描述,将第j个线性层与第j个MGNL层的组合,称为第j层.

依据式(25),可知第m层内的线性层权值梯度信息的反向传播过程为

其中,神经网络输出值a与标签值y之间损失值为L.

依据式(23)～ (25),可知线性层权值的梯度信息在由m层传递至m-1 层的过程为

根据式(28),有

将式(29)代入式(27),有

式(30)阐述了线性层权值的梯度信息由最后一层传递至第m-1 层的传递过程.

同理,依据式(21),(22)和(30)可继续推导线性层权值的梯度信息由最后一层向第m-2 层传递的过程为

线性层权值的梯度信息由最后一层传递至第m-3层的传递过程为

线性层梯度信息由最后一层传递至第j层的传递过程为

线性层中偏置B的梯度信息反向传播过程与线性层权值W的反向传播过程原理一致,此处不再赘述.在此给出线性层偏置B的梯度信息由最后一层传递至任意j层的传递过程,即

下面对多层MGNN 中Mp的梯度信息反向传播过程进行分析.

依据式(24)和式(25),可知Mp梯度信息由损失函数传递至第m层的传递过程为

依据式(22)～ (24)和式(35)可知,Mp梯度信息在由m层传递到m-1 层的过程为

同理,可以得到Mp梯度信息由最后一层传递到任意j层的传递过程为

3 MGNN 辅助理论

3.1 MGNL 信息湮灭问题及反信息湮灭策略

在MGNL 执行过程中,由于Mp矩阵中元素被随机初始化且参与神经网络训练过程,因此在神经网络训练完成之前无法得知其中元素值的大小.为了分析MGNL 运行过程中MPS 过程对根节点原始特征信息产生的影响,取以下两种特殊情况进行讨论:

情形1.Mp矩阵中所有数据均为0 时,表示样本中的特征数据之间不存在任何关系,即相互独立,此时,式(39)退化为

情形2.当Mp矩阵中除对角线以外的所有数据均为1 时,表示样本中的任意两个特征数据之间都存在关系,即样本的特征数据依据其图结构关系,组成一个强连通图,此时有

分析式(46)～ (51)可知,随着消息传播代数的增多,子孙节点传递到根节点的信息量将远超根节点自身的信息量,即初代节点自身信息将堙灭于海量的子孙节点信息.而通过情形1和情形2 的分析,可知MGNL 运行过程中的确存在根节点信息堙灭的可能.

由式(52)可知,反信息堙灭因子可将初代节点信息值成倍数的扩大,防止初代信息被堙灭.实际应用中α的取值随着信息传播代数n的增加而增加.

3.2 注意力损失函数

图消息传播过程中需要关注作用较大的节点信息,忽视作用较小的节点信息.基于此种考虑,研究人员于2017 年提出图注意力网络(Graph attention network,GAT)[24-26],其基本原理是各节点更新隐藏层输出时,通过对其相邻节点进行注意力计算,为每个相邻节点分配不同的权重,权重高的节点视为神经网络注意力集中点.为了获得每个节点的权重,首先需要根据输入的特征值进行至少一次的线性变换得到输出的特征值,因此,需要对所有节点训练一个权值矩阵Wa,其中Wa为n×n的方阵.实践过程中,为了加强注意力机制的处理能力,会在线性变换之后附加一个非线性激活变换,如使用ReLU激活函数进行非线性激活变换,最后将变换后的数据通过softmax 激活函数获得为每个相邻节点所分配的不同权重.

分析GAT 中的注意力机制可以发现,整个过程需要经历线性变换以及softmax 函数的激活,待训练参数量多,计算过程复杂.为了降低注意力机制的实现成本,本文在损失函数中加入对Mp的L2正则化,组成注意力损失函数AL,AL描述为

AL由两部分构成,L(a,y) 为网络最终预测值a与目标值y之间的损失值,L(·) 为损失函数,一般为均方差损失函数或者交叉熵损失函数等;0.5λ‖Mp‖2为注意力限制条件,实际性质类似于L2正则化,其中,λ为注意力限制系数,0＜λ ＜1.

由第1 节分析可知,Mp是将Mg对角线元素全部设置为0 后得到,Mp中除对角线元素外,里面每一个值代表了边的权值,样本特征数据依据Mp进行MPS 过程.通过式(5)可知,在图消息传递过程中,边的权值决定了子节点向父节点传递消息的多寡,故在MGNL 中可以通过约束边的权值实现与GAT 相同的注意力机制.

在神经网络训练过程中,利用梯度下降法不断减小AL值,为了突出阐述AL在网络训练过程中如何产生注意力效果,主要进行针对Mp梯度下降的过程分析.

依据链式求导法则与第2 节中信息反向传播分析可知,由AL决定的针对Mp的反向传播梯度为

对Mp进行梯度下降更新

在MGNN 的损失函数中添加对Mp的L2正则化,结合梯度下降法可以使Mp对自身元素进行筛选,即将连接关系不紧密的特征值之间边的权值进行削弱,保留连接紧密的边的权值,并对其加强.由式(5)可知,边上权值的大小决定了子节点向父节点传递信息的多少,权值越大,则子节点向父节点传播的信息越多,即父节点对子节点的关注度越高;边上权值越小,则表示子节点向父节点传播的信息量越少,即父节点对子节点的关注度减弱,由此实现MGNN 的注意力机制.

AL通过改变损失函数的结构实现原本需要通过复杂线性变换与激活变换才能实现的注意力机制,在实现注意力机制的同时,降低网络的复杂程度,同时减少了神经网络中待训练的参数量.

为了更加直观清晰地对MGNN 进行整体性的描述,基于上述各部分的分析,给出MGNN 运行流程图,如图4 所示.

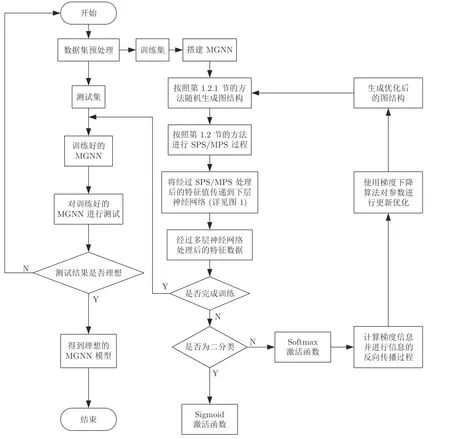
图4 MGNN 运行流程图Fig.4 Operation flow chart of MGNN

4 实验

本节设计了3 组对比实验,实验中所使用的数据集为UNSW_NB15、NSL_KDD和CICDoS2019数据集.

各组实验的目的分别为: 第1 组验证MGNN的有效性以及探索MPS 过程中子孙消息传播代数对神经网络性能的影响;第2 组验证反信息堙灭因子α的重要性;第3 组实验验证注意力损失函数的重要性.

在第1 组和第2 组实验中,MGNN 所使用的损失函数为AL,其余神经网络所使用的损失函数均为交叉熵损失函数.

由于图神经网络(GNN)只能处理样本间的已知图结构关系,而入侵检测数据集中样本间的图结构关系均未知,因此无法应用于网络入侵检测领域,目前也未发现有将GNN 用于入侵检测的文献,因此未将MGNN 与GNN 进行性能对比.

实验中使用的深度学习框架为Tensorflow 2.1.0 (CPU 版),机器学习库为scikit-learn 0.23.2,操作系统为Windows10,编程语言为Python 3.7.4.

4.1 对比实验1

在本部分中,主要对比了深度MGNN 与经典深度学习算法(DNN/CNN/RNN/LSTM)、经典机器学习算法(DT (Decision tree)/SVM (Support vector machine)/KNN (K-nearest neighbor)/RF(Random forest)/LR (Logistic regression))在入侵检测数据集上的性能表现,以此验证MGNN 的有效性,同时探索MGNL 中子孙节点消息传播代数对神经网络性能的影响.其中,基于MGNN 的神经网络又依据其子孙消息传播代数不同划分为: MGNN1、MGNN3、MGNN5、MGNN7、MGNN9.本节中各神经网络的搭建均为序列化结构,深度MGNN 由MGNNSB 按顺序串联堆叠而成,MGNNSB 的结构如图5 所示.

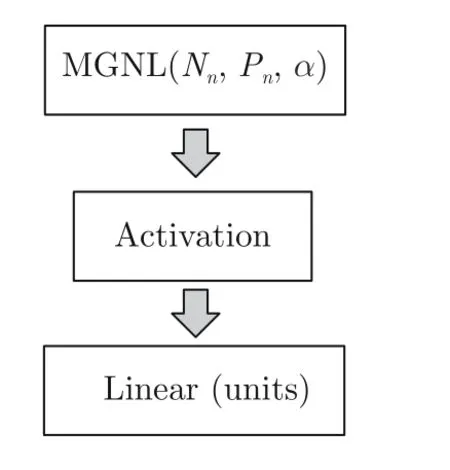
图5 MGNNSB 描述Fig.5 Description of MGNNSB structure

在MGNNSB 中,MGNL 层的Nn为样本特征值的图结构中节点的个数,在第1 层MGNNSB 中为输入样本的特征数据的维度,其后各层MGNNSB中,MGNL 层的Nn由上一个MGNNSB 输出数据的维度决定;Pn为子孙节点消息传播的代数,在MGNN1 中Pn为1,MGNN2 中为2,以此类推.α为反信息堙灭因子,在本组实验中,α均设置为1,即不考虑反信息堙灭措施.实验中MGNN 具体参数设置详见表1 所示.

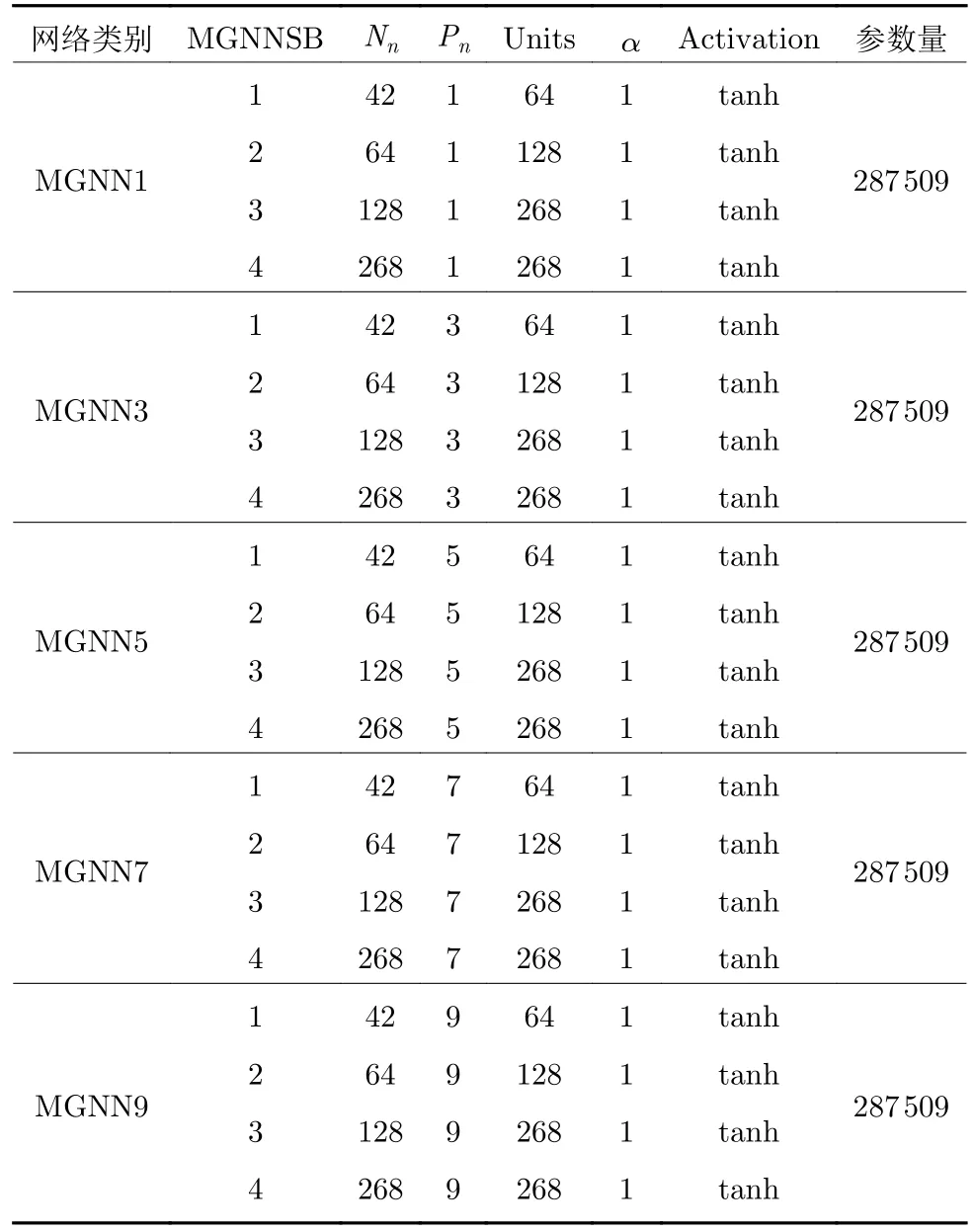
表1 MGNN1～ MGNN9 网络各参数设置Table 1 Various parameter settings in the MGNN1～ MGNN9 networks

在表1 中,MGNNSB 表示组成MGNN 中MGNNSB 的编号,Nn表示MGNNSB 中MGNL层设置的图结构中节点个数,Pn表示MGNNSB中MGNL 层内子孙节点消息传播的代数,Units 表示MGNNSB 中线性层所设置的神经元个数.

图6～ 9 分别为MGNN1～ MGNN9和DNN对UNSW_NB15、NSL_KDD 数据集进行二分类、多分类时神经网络训练过程中的损失值、准确率随迭代次数变化的折线图.

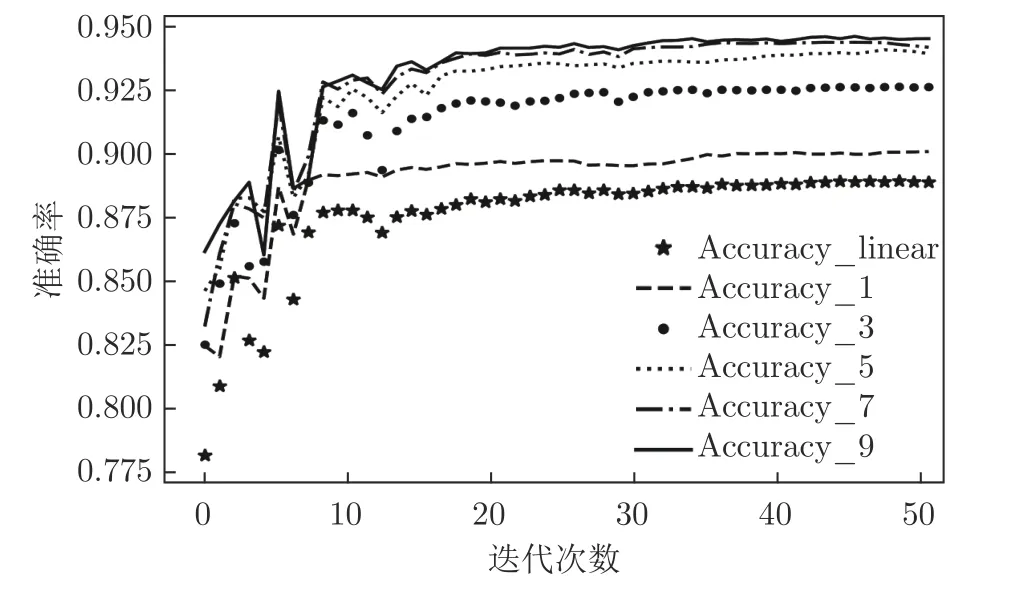
图6 各神经网络对UNSW_NB15 进行二分类Fig.6 Each neural network performs a binary classification experiment on the UNSW_NB15

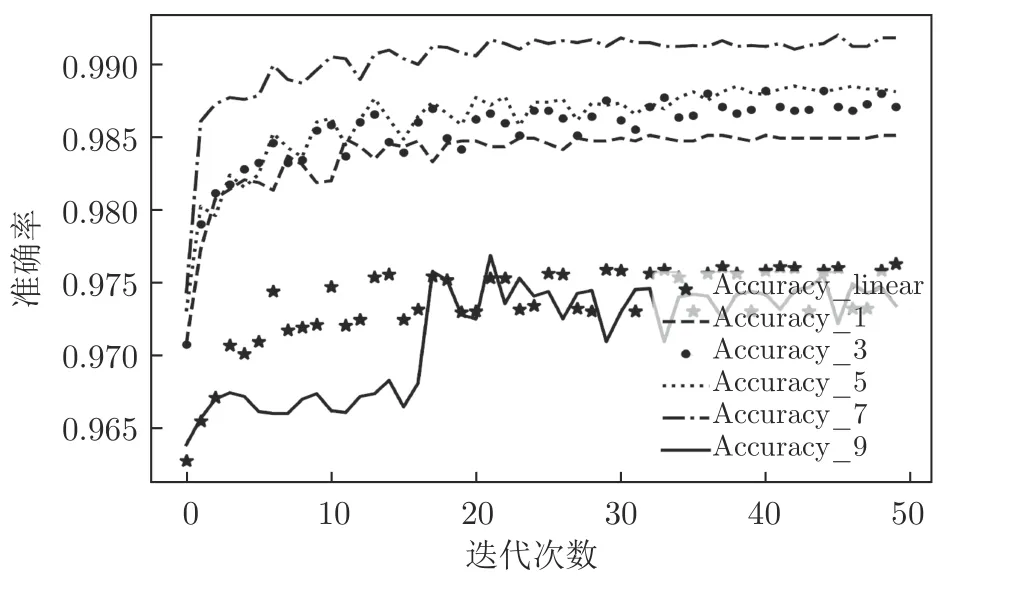
图7 各神经网络对NSL_KDD 进行二分类Fig.7 Each neural network performs a binary classification experiment on the NSL_KDD

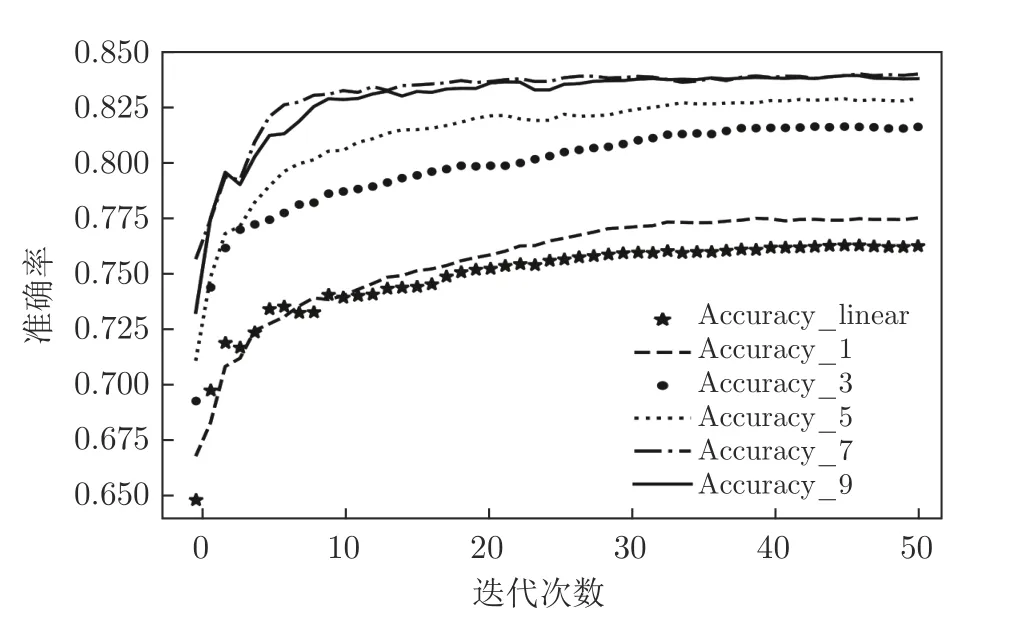
图8 各神经网络对UNSW_NB15 进行多分类Fig.8 Each neural network performs multiclassification experiments on the UNSW_NB15

Accuracy_1 表示MGNN1 训练过程中的准确率变化趋势图,Accuracy_3 表示MGNN3 训练过程中的准确率变化趋势图,以此类推;Accuracy_linear 表示由线性层堆叠而成的DNN 训练过程中准确率变化趋势图.

通过图6～ 9 可知,MGNN1、MGNN3、MGNN5、MGNN7、MGNN9 最终准确率普遍高于DNN,只有在对NSL_KDD 数据集进行二分类与多分类的训练过程中,MGNN9 的准确率低于DNN,尤其是在对NSL_KDD 数据集进行多分类的过程中,MGNN9 的准确率仅为0.5 左右.通过第3.1 节的分析可知,主要是由于本节实验中未启用反信息堙灭策略,子孙信息将父代信息堙灭所导致,由于本节实验重点并不在于分析反信息堙灭策略的作用,故后续分析将不考虑对NSL_KDD 数据集进行二分类和多分类任务时MGNN9 的性能.

通过图6 可知,MGNN1、MGNN3、MGNN5、MGNN7、MGNN9 在对UNSW_NB15 进行二分类实验时,前期准确率经过一个短暂且非常明显的不稳定振荡过程,对NSL_KDD 进行二分类实验时,振荡过程相对平缓;而图9 显示MGNN1～ MGNN9网络在对NSL_KDD 进行多分类实验过程中,准确率收敛过程也较UNSW_NB15 多分类实验平稳,这主要是因为初始化的样本特征数据图结构并不能很好地反映隐藏于样本特征数据中的真实图结构,随着训练过程的持续,神经网络将不断接近真实样本特征数据的图结构,训练过程趋于平稳.上述现象也从侧面反映了隐藏于NSL_KDD 样本特征数据背后的图结构比隐藏在UNSW_NB15 样本特征数据背后的图结构简单.而实际上UNSW_NB15 数据集是澳大利亚安全实验室于2015 年在真实网络环境下采集得到的,相比于NSL_KDD数据集更能体现实际网络数据特征,也更加复杂,这也从侧面反映了本文所设计的MGNN 的有效性.

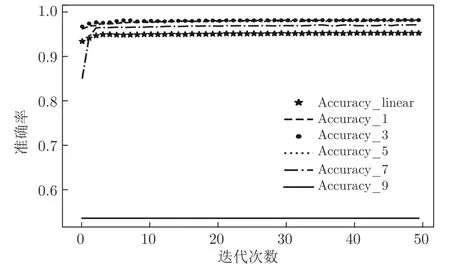
图9 各神经网络对NSL_KDD 进行多分类Fig.9 Each neural network performs multiclassification experiments on the NSL_KDD

进一步分析图6～ 9 可知,在不考虑父辈信息堙灭的前提下,随着子孙节点消息传播代数的增加,MGNN1、MGNN3、MGNN5、MGNN7、MGNN9的性能均逐步提升,同样验证了本文所提出的样本特征数据内部隐藏的图结构信息有助于神经网络性能提升的理论分析.

表2～ 5 详细描述了MGNN1、MGNN3、MGNN5、MGNN7、MGNN9 与DNN、CNN、RNN、LSTM、RF、LR、KNN、DT、SVM 等经典深度学习算法、机器学习算法对NSL_KDD、UNSW_NB15数据集进行二分类和多分类任务时的准确率(Accuracy)、精确率(Precision)、召回率(Recall)、F1-score 值.其中,RF、LR、KNN、DT、SVM 的相关指标数据来源于文献[27],实验中使用的CNN 为Inception v1 分类模型;由于缺少能直接用于入侵检测领域的经典RNN,LSTM,DNN 模型,故实验中使用的RNN、LSTM、DNN 为自行搭建的神经网络模型,搭建以每层网络中神经元个数与MGNN相接近为原则,其中,RNN 具有8 层循环神经网络层,每层分别有42,64,64,128,128,268,268,268个神经元,并返回全部序列数据;LSTM 同样具有8 层长短期记忆网络层,每层同样分别有42,64,64,128,128,268,268,268 个神经元,并返回全部序列数据;DNN 由8 层全连接层所组成,分别具有42,64,64,128,128,268,268,268 个神经元.

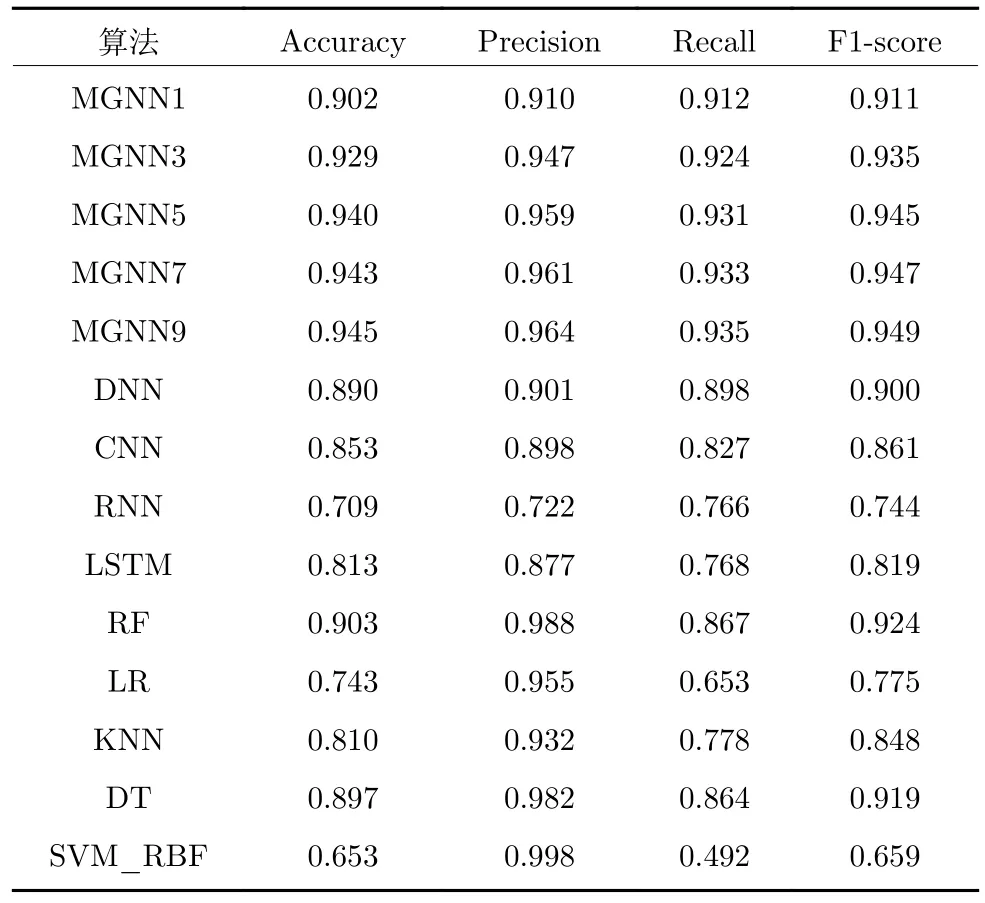
表2 各算法对UNSW_NB15 数据集二分类测试的结果Table 2 The experimental results of the binary classification test of each algorithm on the UNSW_NB15 dataset

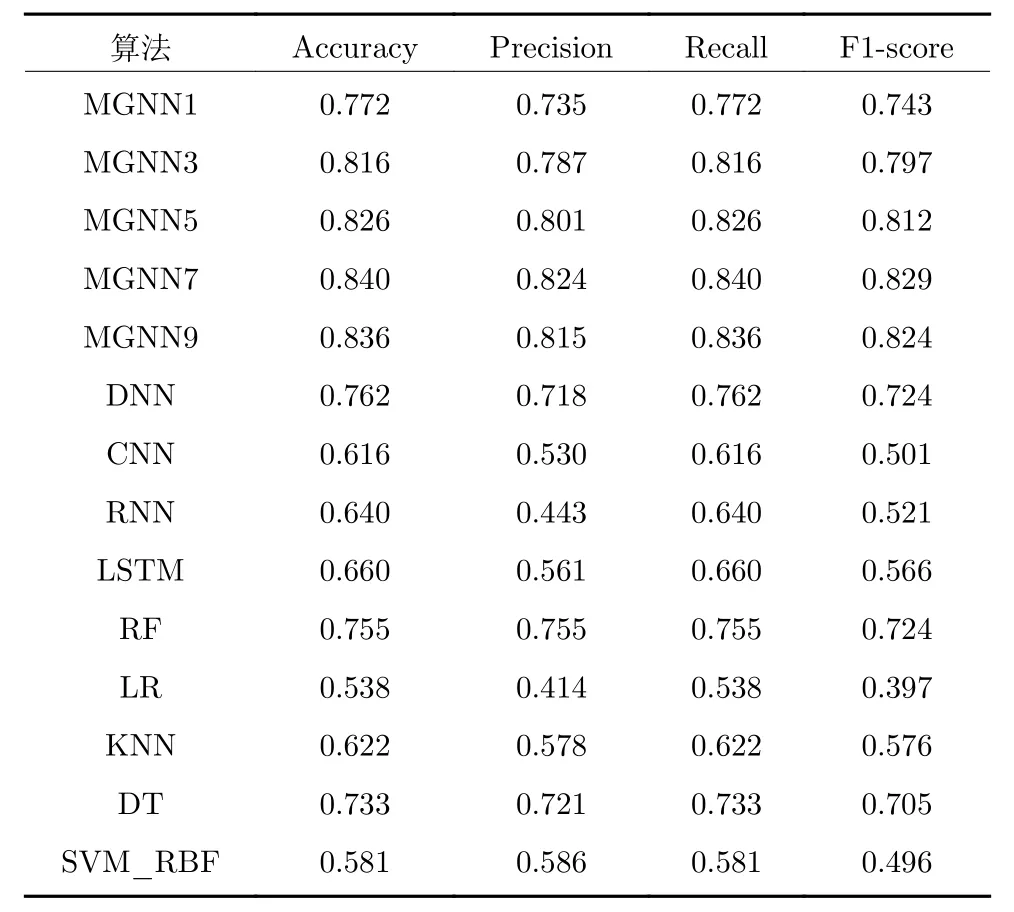
表3 各算法对UNSW_NB15 数据集多分类测试的结果Table 3 The experimental results of the multi-classification test of each algorithm on the UNSW_NB15 dataset

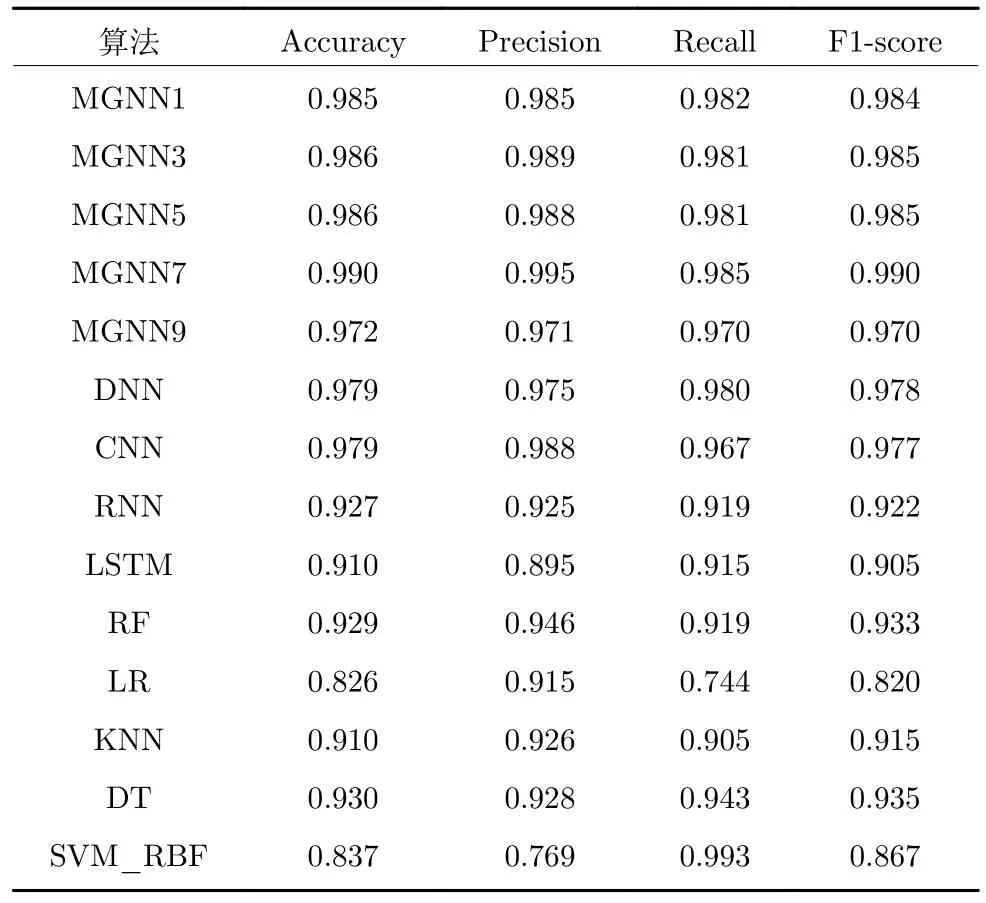
表4 各算法对NSL_KDD 数据集二分类测试的结果Table 4 The experimental results of the binary classification test of each algorithm on the NSL_KDD dataset

表5 各算法对NSL_KDD 数据集多分类测试的结果Table 5 The experimental results of the multi-classification test of each algorithm on the NSL_KDD dataset

由表2～ 5 可知,相对于经典深度学习算法和机器学习算法,能够挖掘并利用特征值之间隐藏的图结构关系的MGNN 在处理网络入侵数据时更具有优势,有效地证实了本文所提出MGNN 的有效性.

为了进一步证实MGNN 的有效性,本节将MGNN 与LSTM-RESNET[28]、NDAE[29]、文献[30]的算法、DCCNet[5]、IGAN-IDS[31]、ELM[32]、OS_ELM[33]、LSTM-RNN[34]、TSDL[35]等近年来基于深度学习的优秀入侵检测算法进行性能对比,图10反映了MGNN 与上述算法对NSL_KDD、UNSW_NB15 数据集进行测试时准确率的对比.

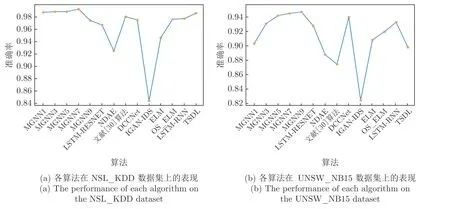
图10 MGNN 与最新入侵检测算法对比Fig.10 Performance comparison between MGNN and the latest intrusion detection algorithms on different datasets

由图10 可知,相对于目前较新的基于深度学习的入侵检测算法而言,在对NSL_KDD、UNSW_NB15 数据集进行测试时,元图神经网络MGNN 具有最高的准确率,由此可以证明在基于深度学习的入侵检测算法中,本文所提出的MGNN 具有一定的应用价值.

为了更进一步验证MGNN 的有效性,本文使用CICDoS2019 数据集对MGNN 性能进行测试,并与朴素贝叶斯算法(Naive Bayes,NB)、决策树算法(DT)、逻辑回归算法(LR)、随机森林算法(Random forest,RF)、Booster、SVM、DDoSNet[36]等算法进行性能指标对比(上述算法在CICDoS2019数据集上的各项性能指标均来自文献[36]).MGNN为MGNN12 (12 代表样本特征值的图结构中节点的个数),实验结果详见表6.

表6 各算法对CICDoS2019 数据集测试Table 6 Test results of each algorithm on the CICDoS2019 dataset

由表6 可知,在使用CICDoS2019 数据集对MGNN12 进行测试时,MGNN12 的性能优于NB、DT、RF 与Booster 算法,在Accuracy 方面,MGNN12 的性能表现相对于NB、DT、LR、RF、Booster、SVM、DDosNet 算法处于中等水平.在Precision方面,MGNN12 对Attack 类型数据检测的Precision 值为0.99,与DDosNet 算法相一致,仅次于NB、RF 算法,DT、Booster 算法在对Attack 类型数据进行检测时的Precision 值最低,分别比MGNN12低0.29、0.23;MGNN12 在对Benign 类型数据进行检测时的Precision 值为1.00,与DDosNet 算法相同,二者在该指标上并列最高,均高出NB 算法0.47.在Recall 方面,MGNN12 对Attack 类型数据进行检测时的Recall 值为0.79,相对于表6 中其他算法而言,仅高于NB 算法与RF 算法;在对Benign 类型数据进行检测时,MGNN12 的Recall 值为0.93,仅高于DT、Booster算法.由上述分析可知,MGNN12 在Precision 指标方面相对于表6 中其他算法处于较优水平,但在Recall 指标方面MGNN12 相对于其他算法并没有明显优势,当精确率和召回率发生冲突时,很难对模型进行比较.而F1-score 值同时兼顾了精确率和召回率,可以看作是精确率和召回率的一种调和平均,能够更好地评价模型.仔细分析表6 中F1-score 一列可知,MGNN12在面对Attack 类型数据时,F1-score 值为0.88,仅次于LR、SVM、Booster 算法;面对Benign类型数据时,F1-score 值为0.96,仅次于DDosNet算法.由上述分析可知,MGNN12 的整体性能低于LR、SVM、DDosNet 算法,高于NB、DT、RF、Booster算法,整体性能处于中等偏上水平,这主要是由于CICDoS2019 数据集特征数目较多(87 个),本文提出的MGNN 在处理该数据集时并未采用其他辅助降维措施与特征选择算法,使得MGNN 在挖掘隐藏于特征数据后的图结构关系时较为困难.

综上所述,在进行网络入侵数据二分类与多分类的任务中,在不考虑父代信息堙灭的情况下,在一定范围内,MGNN 的性能随着MPS 中子孙信息传播代数的增加而提升,MGNN 的性能表现相对于经典深度学习算法和机器学习算法具有明显优势,同时相对于目前新型基于深度学习的入侵检测算法仍具有较明显优势;并且MGNN 在面对3 种入侵检测数据集时都具有不错的性能表现,说明MGNN 具有较强的泛化能力,能够同时适用于多种不同数据集,能够有效地提升入侵检测精度,具有优越的检测性能.

4.2 对比实验2

通过对第4.1 节中图6～ 9、表2～ 5 的分析可知,MGNN1～ MGNN5 随子代信息传播代数的增加,其分类性能逐步提高,但是随着MPS 过程次数的增多,MGNN 的性能却出现了下降的现象.由第3.1 节的理论分析可以推断,MGNN9 出现了父代信息堙灭现象,为了验证第3.1 节的理论分析结论,设置本实验.

在本实验中,将继续使用第4.1 节中MGNN9的网络结构,唯一不同在于本实验将MGNN9 的反信息堙灭因子α设置为2.8,为了便于区分,本实验记MGNN9 为MGNN9_alpha.

图11～ 14 分别展示了MGNN1～ MGNN9、DNN 以及MGNN9_alpha 在对UNSW_NB15、NSL_KDD 数据集进行二分类和多分类时神经网络训练过程中Accuracy 值随迭代次数变化的折线图.

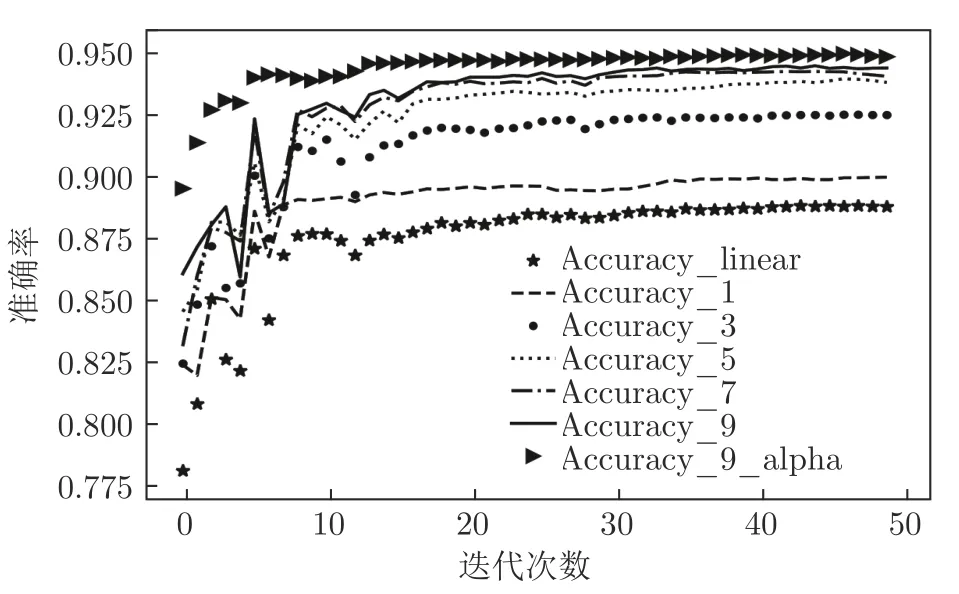
图11 各神经网络对UNSW_NB15 进行二分类Fig.11 Each neural network performs a binary classification experiment on the UNSW_NB15

分析图11～ 14 可知,引入反信息堙灭因子α后,MGNN 神经网络在分类准确率上均有提升,并且训练收敛速度也较大程度加快.

单独分析MGNN9_alpha和MGNN9 可以更加明显地看出,在使用反信息堙灭因子α后,元图神经网络的性能具有明显提升,由此可以证实本文提出的反信息堙灭策略的有效性,该效果在图12和图14 中表现得尤为明显,可以看出MGNN9_alpha 相对于MGNN9 的优越性.

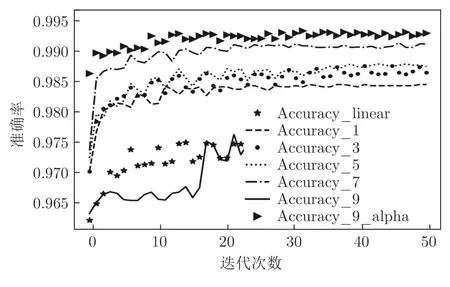
图12 各神经网络对NSL_KDD 进行二分类Fig.12 Each neural network performs a binary classification experiment on the NSL_KDD

图13 各神经网络对UNSW_NB15 进行多分类Fig.13 Each neural network performs multiclassification experiments on the UNSW_NB15

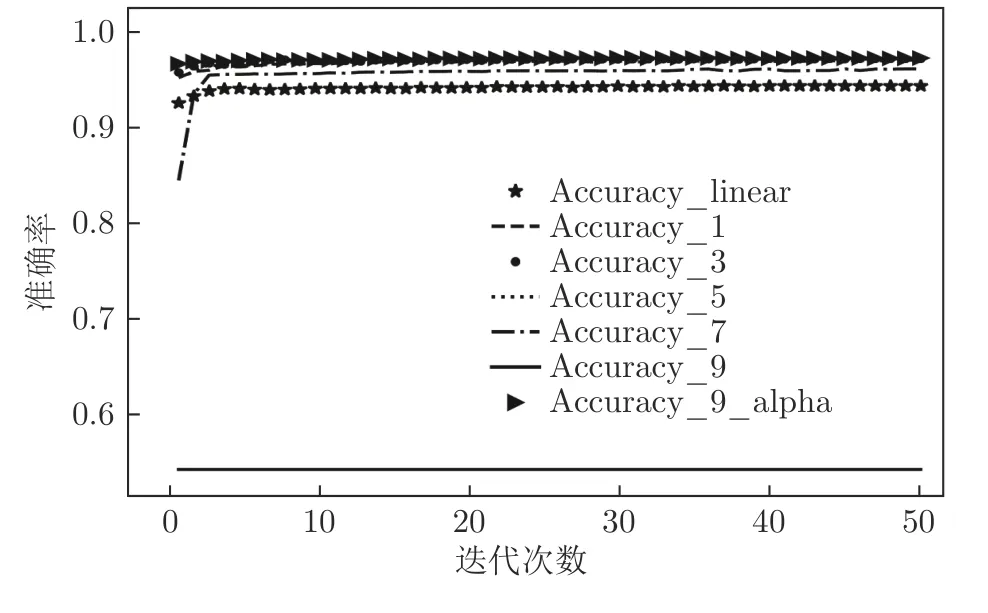
图14 各神经网络对NSL_KDD 进行多分类Fig.14 Each neural network performs multiclassification experiments on the NSL_KDD

为了量化MGNN9_alpha 相对于MGNN9 的性能提升幅度,表7～ 10 展示了MGNN9_alpha、MGNN9 分别对UNSW_NB15 与NSL_KDD 进行二分类和多分类时迭代50 次后的准确率(Accuracy)、精确率(Precision)、召回率(Recall)、F1-score 值.

表7 MGNN9、MGNN9_alpha 网络对UNSW_NB15数据集二分类测试的结果Table 7 MGNN9,MGNN9_alpha networks on the UNSW_NB15 dataset binary classification test results

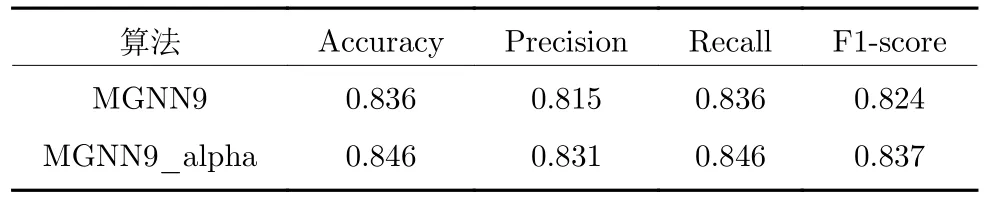
表8 MGNN9、MGNN9_alpha 网络对UNSW_NB15数据集多分类测试的结果Table 8 MGNN9,MGNN9_alpha networks on the UNSW_NB15 dataset multi-classification test results

表9 MGNN9、MGNN9_alpha 网络对NSL_KDD数据集二分类测试的结果Table 9 MGNN9,MGNN9_alpha networks on the NSL_KDD dataset binary classification test results

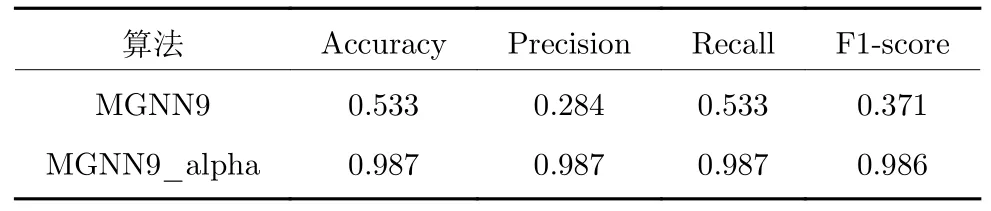
表10 MGNN9、MGNN9_alpha 网络对NSL_KDD数据集多分类测试的结果Table 10 MGNN9,MGNN9_alpha networks on the NSL_KDD dataset multi-classification test results

本实验验证了反信息堙灭因子α在提升MGNN性能方面的重要性,同时也验证了第3.1 节理论分析的正确性.实验证实,引入α后的确能够有效提升MGNN 入侵检测的精度,同时也能够显著地降低误报率.

4.3 对比实验3

本文在第3.2 节详细论述了注意力损失函数的作用,为了验证注意力损失函数的有效性,本文设置了两组元图神经网络,其中一组为MGNN1～MGNN9 使用注意力损失函数,另一组为MGNN1～MGNN9 不使用注意力损失函数,使用这两组MGNN对NSL_KDD、UNSW_NB15 数据集进行二分类和多分类实验,并将各项评价指标的实验结果绘制成折线图,详见图15 所示.

图15 注意力损失函数对MGNN 的影响Fig.15 The effect of attention loss function on MGNN

由图15 可知,在使用了注意力损失函数后,MGNN 的各项评价指标都有明显提高,由此可以证实,本文所提出的注意力损失函数对MGNN 的重要性.

5 结束语

本文针对网络入侵检测场景设计了一种元图神经网络,对图信息传播过程中出现的信息湮灭与注意力机制进行了理论分析.MGNN 能够有效挖掘出入侵样本数据内特征数据间隐藏的复杂联系,并利用上述联系辅助神经网络对入侵数据进行检测.实验结果证明了相对于现有的深度学习算法及传统机器学习算法,MGNN 具有更加优越的入侵检测性能.作为一种新型的神经网络,MGNN 在其他领域的应用尚未涉及,基于MGNN 的各种复杂网络结构尚处于开发状态.未来将继续研究基于MGNN的神经网络结构,尝试将MGNN 与深度强化学习等新技术结合[37-38],开发出更有效的深度学习算法,完善MGNN 的相关理论,扩大MGNN 的应用范围.