基于优化支持向量机的大跨度斜拉桥拉索损伤识别研究

胡庆伟,邹敏石,贺 雁

(湖南陆德工程咨询有限公司,湖南 长沙 410004)

斜拉桥因其优美的造型,强大的跨越能力和合理的受力体系被广泛应用于各类跨江跨河工程。斜拉桥的传力机理明晰,通过锚于桥塔的斜拉索为主梁提供竖向和水平分力,确保主梁维持合理线形,故斜拉索是斜拉桥结构最重要的受力构件之一,其构件损伤水平对桥梁结构整体可靠性的影响十分重大。近年来,各专家学者针对斜拉索的损伤展开了一系列的研究和探索。张绍逸等针对随机车辆荷载作用下的大跨度斜拉桥斜拉索损伤诊断问题,提出了一种分布式布里渊光纤感测技术的损伤诊断方法,以南京长江三桥为工程背景,融合蒙特卡洛法建立了基于应变样本的拉索诊断模型[1];陈治邦等为研究斜拉索腐蚀下的斜拉桥体系可靠度,采用串并联理论建立了斜拉索强度的概率密度模型,分析了斜拉索腐蚀疲劳损伤对斜拉桥整体结构的影响[2];郭健等基于小波变换分析了跨海斜拉桥在风致抖动下的斜拉索损伤识别问题,实现了斜拉桥在风振作用下的多尺度损伤指标和损伤位置的预测[3]。

综上可知,目前对于斜拉索的损伤研究主要侧重于斜拉索损伤对结构受力的影响[4,5]。为实现损伤程度和损伤位置的精确预测,提出一种基于优化支持向量机的斜拉桥斜拉索损伤识别方法,通过支持向量机建立斜拉索损伤与主梁挠度增量的关系,并反向推演斜拉索损伤位置和程度,通过实际工程为背景,通过三个损伤工况验证了该方法的可行性。

1 支持向量机算法原理

支持向量机是一种以统计学习为基本理论,鲁棒性较高的机器学习算法[6,7]。假设存在待学习的样本集合A={Xi,Yi}={(x1,y1),(x2,y2),…,(xi,yi)},i为样本最大容量,采用支持向量机算法实现样本集中输入向量X到输出向量Y映射关系的拟合,首先对样本集采用高斯径向基核函数进行高维映射,高斯径向基核函数的表达式见公式(1)

(1)

式中:σ为数据均方差;g为核函数参数。

将样本集进行预处理后,即可建立求解高维数据样本下关于损失函数的最大超平面,由于该问题是求取样本最大超平面的参数,故可建立优化数学模型如公式(2)所示

(2)

式中:Q为关于数据样本最大超平面优化问题的目标函数;w为最大超平面权向量;c为最大超平面惩罚因子;ζi、ξi为最大超平面的松弛因子;ε为损失函数;k为核函数;b为拟合偏差。

为方便求解最大分离超平面的优化问题,引入拉格朗日乘子L(αi,αj)对式(2)进行改造,创建关于拉格朗日乘子极大化的优化问题如公式(3)所示

(3)

通过求解拉格朗日乘子即可解出最大分离超平面的权向量和拟合偏差。

2 斜拉索损伤模型的建立

2.1斜拉索损伤指标建立

斜拉桥在运营过程中,由于受到荷载效应、环境因素等多种不利因素的影响,斜拉索存在腐蚀、老化等不同程度的损伤,当斜拉索受到一定损伤时,由于斜拉索对主梁提供的竖向分力减弱,受损斜拉索与主梁连接截面挠度会与理论计算值存在一定偏差,取主梁截面挠度增量为斜拉索损伤指标,斜拉索损伤下的主梁挠度增量可表示为

Δf=f-fG

(4)

式中:Δf为由斜拉索损伤引起的主梁挠度增量;f为斜拉索损伤状态下的主梁挠度值;fG为斜拉索未受损状态下的主梁挠度理论计算值。

斜拉索受到温度、雨水等不利环境因素作用时,其拉索横截面面积会因拉索腐蚀而减小,为衡量斜拉索因腐蚀作用而造成的损伤程度,采用面积模拟法定义斜拉索在腐蚀作用下的结构损伤程度,如公式(5)所示

(5)

式中:A为斜拉索初始状态下的横截面面积;A′为斜拉索服役状态下的横截面面积;S为斜拉索损伤程度指标。

从斜拉索损伤程度指标的表达式可以看出,斜拉索损伤程度指标S取值范围为[0,1],当S趋近于0时,表示斜拉索处于基本完好状态,当S趋近于1时,表示斜拉索趋于完全腐蚀损伤状态。

2.2 基于SVM的斜拉索损伤识别

为实现对斜拉索损伤的精确识别,以斜拉桥因拉索损伤引起的主梁挠度增量为输入变量,斜拉索损伤位置和损伤程度指标为输出变量,基于支持向量机建立斜拉索损伤识别模型流程如下。

(1)确定输入变量与输出变量。首先根据2.1节中的理论确定支持向量机斜拉索损伤预测的输入变量与输出变量,根据主梁挠度增量变化情况进行反向推演,确定以主梁挠度增量变化-斜拉索损伤定位的非线性映射条件关系。

(2)建立桥梁的有限元数值计算模型。确定不同位置和程度的斜拉索损伤条件为分析样本点,基于有限元数值计算模型计算主梁挠度增量响应,得到关于主梁挠度增量响应-斜拉索损伤条件的样本数据集,对其进行归一化预处理,归一化处理方式如式(6)所示

(6)

式中:u为归一化后的数据;v为归一化前的数据;vmin和vmax分别为样本集中的最小与最大值。

(3)构建SVM的损伤识别模型。定义Y=(y1,y2,…,yn)为斜拉索损伤识别变量,i代表斜拉索位置,数值代表斜拉索损伤程度。以主梁挠度变化增量为输入变量,斜拉索损伤定位及损伤程度为输出变量,基于SVM对样本数据进行学习拟合,定义识别误差为0.005。

(4)验证SVM预测精度是否满足要求。通过有限元验证集的计算结果验证SVM对样本集的拟合精度是否满足要求,满足则输出损伤预测模型及结果,不满足则继续进行训练。

2.3 PSO算法优化SVM斜拉索损伤预测模型

支持向量机算法虽然对强非线性数据具有较高的拟合精度,但其学习效率和精度十分依赖于算法参数和核函数参数的取值,为进一步减小斜拉索损伤识别的误差,提高支持向量机的拟合效率,提出采用粒子群算法优化支持向量机核参数的斜拉索损伤模型。通过粒子群算法优化支持向量机的斜拉索损伤识别过程如下。

(1)初始化粒子群参数,确定粒子维度信息,在斜拉索损伤识别模型的待优化变量中,将惩罚因子c和核参数g分别取为两个维度上的信息。

(2)更新粒子适应度值,并确定个体最优与群体最优,判断是否满足终止迭代条件

(3)满足终止迭代条件则输出群体最优位置,确定最优参数组合,不满足则更新粒子位置,并重新计算适应度值,返回步骤2。

3 算 例

南益洞庭湖胜天大桥为双塔双锁面钢箱梁斜拉桥,桥梁跨径布置为(182+450+182)m。该桥主梁采用Q345qD钢材,桥塔采用C50混凝土浇筑,斜拉索为高强度钢绞线,桥梁设计荷载等级为公路-I级。

为构建斜拉索损伤识别模型,首先建立桥梁的有限元数值分析模型。采用ANSYS有限元软件对建立该桥的实体有限元模型,斜拉索采用Link10自建单元进行模拟,桥塔混凝土采用Solid65实体单元模拟,主梁钢箱梁采用Beam188梁单元模拟,主梁与斜拉索之间通过MPC184单元连接。

基于有限元模型生成斜拉桥主梁挠度增量-斜拉索损伤程度的样本数据集,表1给出了粒子群算法优化前后支持向量机拉索损伤预测模型的超参数取值结果。从表1可以看出,基于粒子群算法优化后的惩罚因子相较优化前有一定减小,而核函数参数相较优化前偏大。

表1 超参数优化前后对比

为验证粒子群算法对支持向量机拉索损伤识别模型的改进效果,通过10个随机的主梁挠度增量测试点对支持向量机超参数优化前后的模型进行检验,测试样本的预测误差如图1所示。从图1可以看出,对SVM斜拉索损伤模型参数优化前,最大识别误差为0.004 4,最小识别误差为0.001 9,平均识别误差为0.003 3。基于粒子群算法优化支持向量机拉索识别模型超参数的识别误差得到显著降低,最大识别误差为0.002 4,最小识别误差为0.000 6,平均识别误差为0.001 8。所有测试样本中仅有6号样本出现了优化前模型略微高于优化后模型的情况,综合各测试样本的斜拉索损伤识别结果可以得出,粒子群算法对支持向量机斜拉索损伤识别模型的优化效果十分明显。

图1 测试样本误差对比

由于工程结构呈对称分布,以半结构为研究对象,分别取L5号斜拉索损伤程度为25%、L15号斜拉索损伤程度为50%、L25号斜拉索损伤程度为75%三种工况对优化后的支持向量机斜拉索损伤识别模型进行结果验证,图2给出了三种计算工况下的支持向量机预测结果,从图2可以看出,三种测试损伤工况下,基于支持向量机的损伤识别模型对损伤斜拉索的定位分别为L5、L15和L25号斜拉索,与测试斜拉索损伤编号完全一致,说明了该斜拉索损伤识别模型可以精确的定位受损斜拉索的位置。根据模型识别结果,三种损伤工况下斜拉索的损伤预测值分别为24.89%、49.77%和75.23%,与预设工况的相对误差分别为-0.44%、-0.46%和0.31%,所有预测误差均小于0.5%,说明基于支持向量机的斜拉桥拉索损伤识别模型在实际工程应用中的可靠性较高。

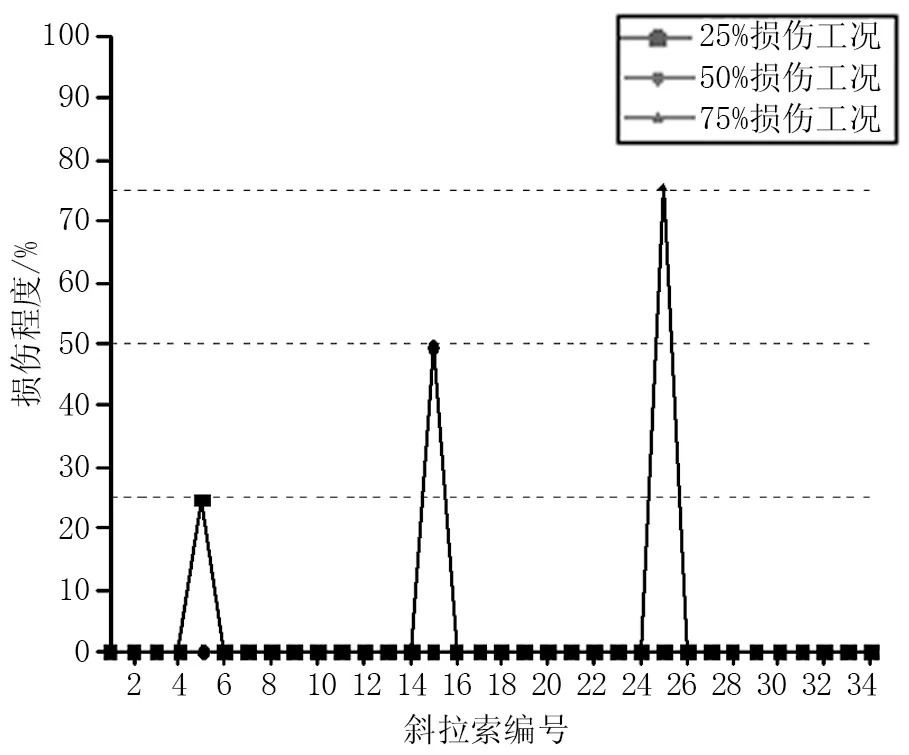
图2 各损伤工况模型预测结果

4 结 论

斜拉索作为斜拉桥的主要受力构件,其损伤位置和状态对整体结构的影响重大,针对大跨度斜拉桥斜拉索的损伤识别问题,提出了一种基于支持向量机算法模型的斜拉索损伤识别方法,通过粒子群算法优化支持向量机的超参数,并通过三种损伤工况验证了该模型的适用性,得到结论如下。

(1)斜拉索的损伤识别问题可以通过斜拉索损伤程度与结构增量响应之间的关系建立基于支持向量机的算法预测模型。

(2)基于粒子群算法优化后的支持向量机模型相较于标准支持向量机模型在几个验证样本的测试中相对误差均更低,达到了精度更高的预测水平。

(3)在25%、50%和75%三个损伤测试工况下,基于优化支持向量机的斜拉索损伤识别模型均衡准确的定位受损斜拉索的位置,且损伤程度预测相对误差均低于0.5%,证明了该模型的可行性。